Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de Ingeniería
Print version ISSN 0121-4993
rev.ing. no.32 Bogotá July/Dec. 2010
Aplicación del método de número de onda discreto en la propagación de ondas SH en medios estratificados
Application of the Discrete Wave Number Method in the SH Waves Propagation in Layered Media
Juan Daniel Moya
Estudiante, Maestría en Ingeniería Civil, Universidad de los Andes. Bogotá D.C., Colombia. jd.moya34@uniandes.edu.co
Recibido 1 de octubre 1 de 2009, modificado 11 de abril de 2010, aprobado 11 de diciembre de 2010.
RESUMEN
El artículo presenta una revisión del método del número de onda discreto (DWN) y su aplicación en el análisis de fuentes lineales en medios estratificados para el caso de ondas SH. El método calcula la función de Green de forma numérica, descomponiendo el campo de desplazamiento como la superposición de ondas planas. La solución se expresa como una ecuación integral sobre el dominio del número de onda horizontal. La evaluación de dicha ecuación implica considerar la presencia de infinitas fuentes distribuidas periódicamente a lo largo del eje horizontal x. La aplicación del método se extiende para calcular la función de Green en medios estratificados. Formulando las condiciones de frontera adecuadas en las interfaces de los estratos. Por último, se presentan los resultados de sismogramas sintéticos calculados para un arreglo unidimensional de receptores en superficie.
PALABRAS CLAVES
Propagación de ondas, número de onda discreto, medios estratificados.
ABSTRACT
This paper presents a review of the discrete wave number method (DWN), and its application in layered media subjected to a lineal source in the case of SH waves. The method allows for the numerical calculation of the Green function; it decomposes the displacement field as a superposition of plane waves. The solution is expressed as an integral equation over the horizontal wavenumber domain. The evaluation of the integral equation implies infinite sources distributed along the horizontal x-axis at equal intervals. The method is used to calculate the Green function in a layered media; the enforcement of boundary conditions at the interface of each layer allows us to find the appropriate coefficients for the plane wave expansion. Finally, seismographs are calculated for a linear array of surface receivers.
KEY WORDS
Wave propagation, discrete wave number, layered media.
INTRODUCCIÓN
El método del número de onda discreto fue propuesto por Bouchon y Aki [1] y ha sido ampliamente usado para estudiar gran variedad de problemas en elasticidad dinámica, y para probar la precisión de otros métodos numéricos como diferencias finitas, elementos finitos, métodos de rayo y técnicas pseudoespectrales (e.g. [2, 3, 4, 5, 6, 7]). Esta técnica permite calcular la función de Green de forma numérica con un desarrollo matemático sencillo y un costo computacional relativamente bajo. En el presente artículo, se abordan algunos aspectos básicos de la formulación del método y aspectos de su convergencia y precisión, comparando soluciones analíticas con las aproximaciones numéricas. Además, se presenta el cálculo de sismogramas sintéticos para un perfil de suelos típico de la sabana de Bogotá, suponiendo una fuente somera que se encuentra en el interior del medio.
PRINCIPIOS DEL MÉTODO
La propagación de ondas generadas por una fuente lineal en un medio elástico puede representarse mediante ondas cilíndricas o, bien, como una superposición de ondas planas homogéneas y no homogéneas. Bajo este último supuesto y denotando a x y z como los ejes horizontal y vertical respectivamente, el campo de desplazamientos armónico en dirección perpendicular al plano se puede escribir de la forma:
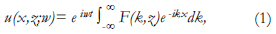
donde ω es la frecuencia y k es el número de onda horizontal. La ecuación (1) representa todo el conjunto de ondas planas emitidas por la fuente hacia el medio. Cuando el medio es infinito y homogéneo, la integral puede ser evaluada y la solución analítica es expresada mediante funciones de Hankel de segunda especie y de orden 0; sin embargo, cuando el medio es finito o si hay heterogeneidad en los estratos, la solución puede presentar singularidades y la evaluación de la integral se torna muy complicada, aún numéricamente. Si en vez de considerar una sola fuente se consideran múltiples fuentes separadas periódicamente una distancia L a lo largo del eje horizontal, la ecuación (1) se trasforma en:
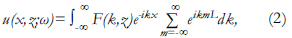
donde L es la periodicidad de las fuentes, y el término adicional es la contribución de cada una de las múltiples fuentes. El término del tiempo eiωt, se omite, pero se entiende que está presente. Según con el teorema de Schwartz [8], se tiene que la sumatoria introducida en la Ecuación (2) colapsa en una serie de pulsos delta de Dirac espaciados periódicamente una distancia L.
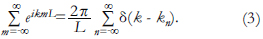
De acuerdo con la Ecuación (3), el integrando de la Ecuación (1) solamente existe para los valores discretos k=kn de la suma en la Ecuación (3). De esta forma, la Ecuación (1) puede ser reescrita como:
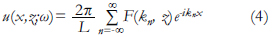
Donde kn es el número de onda discretizado, el cual se expresa como:

Si la serie de la ecuación (4) converge, entonces la sumatoria puede truncarse para obtener una aproximación de la solución; por lo tanto, la ecuación se discretiza como:
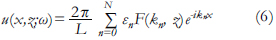
Donde N es el número de términos que se consideran en la aproximación y εn es el factor de Neumann (vale 1.0 para n=0 y 2.0 para n>0), el cual se introduce por la simetría de las fuentes y reduce la evaluación de la suma a la mitad.
Es importante tener en cuenta que la solución planteada en la ecuación (6) considera la presencia de infinitas fuentes distribuidas de manera horizontal, de manera que para obtener la solución debida a una sola fuente se debe aislar la respuesta de las fuentes lejanas. La respuesta de las fuentes aledañas se puede aislar seleccionando una distancia L suficientemente grande, para que las ondas generadas por las demás fuentes no alcancen a llegar a los sitios donde se encuentran los receptores. Otra forma de aislar las ondas provenientes de las fuentes lejanas es introduciendo una pequeña parte imaginaria en la frecuencia, de tal forma que se aumenta la respuesta de los primeros arribos (fuente de interés) con respecto a la respuesta de los arribos tardíos (fuentes aledañas).

El efecto de la frecuencia imaginaria se corrige luego cuando se tiene la solución en el dominio del tiempo. La respuesta impulsiva u(t) se obtiene a partir de la solución u(ω) a través de la relación:
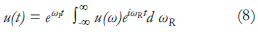
Donde la integral resultante es evaluada con la trasformada rápida de Fourier.
VALIDACIÓN Y CONVERGENCIA DEL MÉTODO
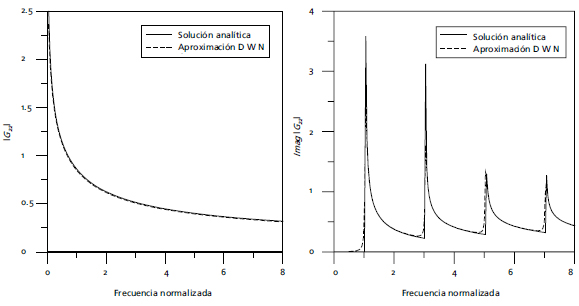
Para validar los cálculos numéricos y analizar la convergencia del método se compararon los resultados con la solución analítica para el caso de un semiespacio y un estrato finito con base rígida. Las soluciones corresponden a una fuente lineal de ondas SH. En la Figura 1, se muestran las funciones de Green obtenidas mediante el DWN para una aproximación con 1000 términos, junto con las soluciones analíticas de cada caso. Para el caso del semiespacio se consideró que la fuente se encuentra en el interior del medio; se observa que las soluciones son prácticamente iguales para todo el rango de frecuencias. Para el caso de base rígida, se calcula la parte imaginaria de la función de Green para fuente y receptor coincidentes en la superficie; se observan ligeras diferencias alrededor de las singularidades, lo cual se debe a que la base rígida es aproximada en el cálculo numérico, como un semiespacio de rigidez finita.
Figura 1. Comparación entre la función de Green calculada por el DWN y la solución exacta en función de la frecuencia normalizada ƒτ(τ = 1.25 s.). A la izquierda se presenta el modulo de la función de Green para el caso del semiespacio y a la derecha se muestra la parte imaginaria de la función de Green para fuente y receptor coincidentes en la superficie de un estrato finito con base rígida (ver [9] ).
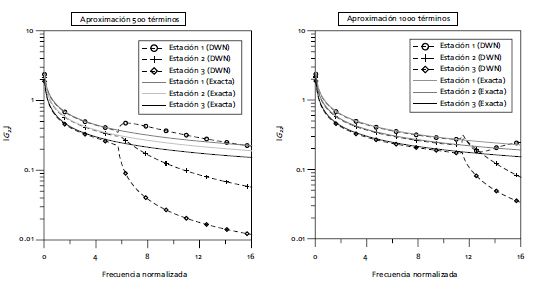
Los anteriores resultados muestran que para el rango de frecuencias considerado la aproximación numérica es bastante buena, considerando 1000 términos en la ecuación (6); sin embargo, en la medida que el rango de frecuencias se hace más amplio, la aproximación comienza a alejarse de la solución exacta para un determinado número de términos. Con el propósito de analizar la convergencia del método se realizaron cálculos para el caso del semiespacio elástico considerando diferentes términos de la serie y diferente periodicidad de las fuentes. En la Figura 2, se presenta la solución evaluada en superficie para diferentes puntos ubicados a lo largo del eje x, considerando 500 y 1000 términos en la serie. Se observa que, en cuanto más términos se involucren en el cálculo, el rango de frecuencias para las cuales se tiene una buena aproximación es mayor. Por otro lado, se aprecia que la divergencia de la aproximación con respecto a la solución analítica se amplifica en cuanto más alejado se esté de la fuente.
Figura 2. Convergencia en función del número de términos de la serie
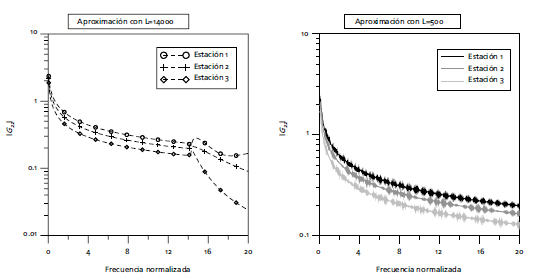
Otro parámetro que juega un papel importante en la convergencia del método es la periodicidad que se elija para las fuentes. En la Figura 3 se presentan los resultados de la función de Green para el caso del semiespacio elástico, calculadas con diferentes valores de L y considerando un valor fijo de 500 términos en la Ecuación (6). A medida que el valor de L aumenta, la solución es suave aunque se tienen divergencias a altas frecuencias; por otro lado, cuando el valor de L es muy pequeño, se eliminan las divergencias de la función en altas frecuencias pero se presentan oscilaciones que distorsionan el resultado.
Figura 3. Convergencia en términos de la periodicidad de las fuentes
La selección de la periodicidad dependerá de la naturaleza del problema. Este valor debe ser suficientemente grande para garantizar que durante el tiempo de observación, las ondas provenientes de las fuentes cercanas no afecten los resultados. En la práctica, se suele calcular el valor de L con respecto a la velocidad del estrato más rígido y el tiempo de observación; no obstante, se debe tener en cuenta que esto puede implicar un gran costo computacional ya que se deben considerar bastantes términos de la serie para no tener divergencias de la función de Green a frecuencias bajas (inferiores a la frecuencia máxima de interés).
APLICACIÓN A MEDIOS ESTRATIFICADOS
La descomposición del problema inicial en ondas planas, facilita el análisis de la propagación en medios heterogéneos, siempre y cuando se trate de estratos horizontales que cambien sus propiedades solamente con la profundidad. Si los estratos son horizontales, las únicas ondas que pueden existir son las reflejadas, las refractadas y las que produzca la fuente lineal. De esta forma, se puede escribir el campo de desplazamientos como:
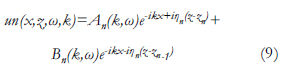
Donde x y z son los ejes horizontal y vertical, ω es la frecuencia circular, k es el número de onda horizontal, An y Bn son los factores de amplitud de las ondas que se propagan en cada estrato y el valor de ηn está dado por:
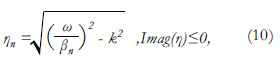
donde βn es la velocidad de onda de corte del estrato considerado. En el estrato donde se encuentra la fuente, además de las ondas ascendentes y descendentes, deben tenerse en cuenta las ondas emitidas por la fuente misma.
De los parámetros considerados en la Ecuación (9), se desconocen los valores de An y Bn, los cuales son función del número de onda k, y de la frecuencia ω. Los valores de los coeficientes pueden ser hallados formulando las condiciones de frontera en las interfaces de cada estrato. En superficie libre se debe cumplir que los esfuerzos cortantes sean nulos y en las interfaces de cada estrato debe existir compatibilidad de esfuerzos y desplazamientos. Con estas condiciones se construye un sistema de ecuaciones simultáneas, que debe ser solucionado para cada ω y cada k.
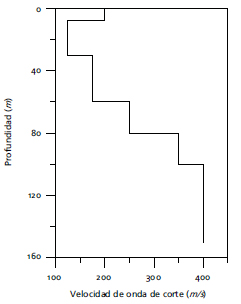
Para ilustrar el cálculo de la función de Green en medios estratificados mediante el método DWN, se analizó una columna estratigráfica típica de la sabana de Bogotá. El perfil estratigráfico está caracterizado por suelos blandos correspondientes a las arcillas lacustres de la formación Sabana seguido por intercalaciones de areniscas y arcillas de la formación Subachoque. En la Figura 4 se presenta el perfil de velocidades asumido para el cálculo. Para la señal de la fuente se usó un pulso de Ricker, el cual permite tener un control directo sobre la duración, el rango de frecuencias y la frecuencia predominante de la excitación forzada. La expresión analítica del pulso de Ricker está dada por:
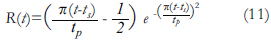
donde tp es el período característico del pulso y t s es un parámetro que traslada el pulso a lo largo del eje del tiempo. Los parámetros usados para el cálculo de sismogramas son ts =1.5 s y tp =0.5 s.
Figura 4. Perfil de velocidades de onda de corte usado para el análisis
Los sismogramas sintéticos se calcularon considerando la fuente a una profundidad de 300m y son presentados en la Figura 5. Los diferentes receptores se ubicaron en superficie, centrados con respecto a la coordenada x de la fuente. Se observa claramente el primer arribo de la señal en todos los receptores, junto con los demás arribos generados por las reflexiones de los estratos. Los sismogramas reflejan la atenuación geométrica que se presenta en los receptores más lejanos, la cual es proporcional al inverso de la distancia.
Figura 5. Sismogramas sintéticos calculados para el perfil de suelos considerado
Por otro lado, se puede observar que los receptores más lejanos muestran sismogramas más largos con movimientos importantes después de haber acabado la vibración forzada del sistema, mientras que los sismogramas de los receptores más cercanos son más cortos. Este efecto se observó en Bogotá durante el sismo de Quetame del 24 de mayo de 2008, en el cual se registraron movimientos importantes tiempo después de la fase intensa del movimiento en varias estaciones de acelerógrafos instalados en la ciudad. Estos movimientos se deben a ondas superficiales que quedan atrapadas en los estratos más blandos y superficiales del depósito.
Debido a la naturaleza del problema considerado en el presente artículo, sólo aparecen desplazamientos horizontales en el antiplano y ondas superficiales tipo Love; no obstante, la formulación del método puede extenderse sin mucha dificultad, para las demás componentes de movimiento en 2D y 3D. El método también puede utilizarse en conjunto con otras técnicas numéricas como elementos de contorno (BEM, IBEM), para el modelado de grandes cuencas [10], o para la interpretación de ensayos geofísicos donde se tiene bien controlada la fuente con el fin de identificar el arribo de los diferentes tipos de ondas sísmicas.
CONCLUSIONES
El método del número de onda discreto es una herramienta útil para el cálculo de la función de Green en medios estratificados. El método se basa en la descomposición en términos de ondas planas y la presencia periódica de infinitas fuentes para trasformar el problema de una integración continua en una sumatoria discreta.
La convergencia del método depende de dos factores. Por un lado, se encuentra la cantidad de términos que se considera para el cálculo de la serie y, por otro, está la periodicidad de las fuentes; ambos parámetros controlan la discretización del número de onda. Comparando las soluciones analíticas con las soluciones numéricas se concluye que puede haber dos tipos de divergencias. La primera tiene que ver con el rango de valores para los cuales se evalúa el valor de k, entre mayor sea el rango, se tiene una mejor aproximación en un amplio rango de frecuencias. La segunda tiene que ver con el incremento de k que se seleccione, a menor incremento mayor precisión en la solución. Si, por el contrario, se escoge un incremento muy grande se obtienen oscilaciones con respecto al valor medio, que distorsionan el resultado.
En el presente escrito se aplica el método para medios verticalmente heterogéneos, imponiendo las condiciones de frontera en las interfaces. Esto permite calcular funciones de Green para estratigrafías más complejas y calcular sismogramas sintéticos. En particular, se muestra un ejemplo típico de un perfil de suelos en la sabana de Bogotá. Los sismogramas calculados muestran el atrapamiento de ondas en los estratos superficiales, fenómeno que explica la aparición de ondas tiempo después de la fase intensa del sismo de Quetame.
La facilidad de la formulación y la versatilidad del método permiten que pueda usarse en conjunto con otras técnicas numéricas, esto hace que el DWN sea una herramienta de gran aplicación para la modelación de la fuente sísmica, el efecto de la estratigrafía, la geometría de las cuencas y la interpretación de ensayos geofísicos.
REFERENCIAS BIBLIOGRÁFICAS
[1] M. Bouchon and K. Aki. "Discrete Wave number Representation of Seismic Source Wave Fields". Bulletin of the Seismological Society of America, Vol. 67, No. 2, April 1977, pp. 259-277. [ Links ]
[2] R. Stephen, F. Cardo-Casas and C. Cheng. "Finite-difference Synthetic Acoustic Logs". Geophysics, Vol. 50, No. 10, October 1985, pp. 1588-1609. [ Links ]
[3] C. Saikia and R. Herrmann. "Moment-tensor Solutions for three 1982 Arkansas Swarm Earthquakes by Waveform Modeling". Bulletin of the Seismological Society of America, Vol. 76, No. 3, June 1986, pp. 709-723. [ Links ]
[4] W. Beydoun and T. Keho. "The Paraxial Ray Method". Geophysics. Vol. 52, No. 12, December 1987, pp. 1639-1653. [ Links ]
[5] V. Maupin. "The Radiation Modes of a Vertically Varying Half-space: A New Representation of the Complete Greens Function in Terms of Modes". Geophysical Journal International, Vol. 126, No. 3, Sepetember 1996, pp. 762-780. [ Links ]
[6] S. Aoi and H. Fujiwara. "3D Finite-difference Method Using Discontinuous Grids". Bulletin of the Seismological Society of America, Vol. 89, No. 4, August 1999, pp. 918-930. [ Links ]
[7] P. Moczo, M. Lucka, J. Kristek, and M. Kristekova. "3D Displacement Finite Differences and a Combined Memory Optimization". Bulletin of the Seismological Society of America, Vol. 89, No. 1, February 1999, pp. 69-79. [ Links ]
[8] L. Schwartz. Théorie des Distributions. Paris: Hermann, 1966. [ Links ]
[9] F. J. Sánchez-Sesma, F. Scherbaum, F. Luzón, M. Santoyo, A. García, A. Rodríguez, M. Perton, M. Campillo y R. Weaver. (2009 July). "Energy Densities of Diffuse Seismic Field as a Tool for Imaging". Presentado en: Noise and diffuse wavefields, Neustadt, Alemania. [ Links ]
[10] M. Bravo, F. J. Sanchez-Sesma and F. Chavez. "Ground motion on stratified alluvial deposits for incident SH waves". Bulletin of the Seismological Society of America, Vol. 78, No. 2, April 1988, pp. 436-450. [ Links ]