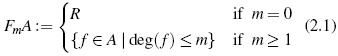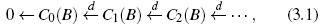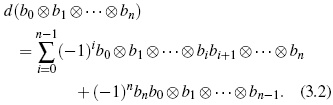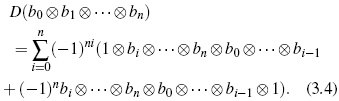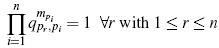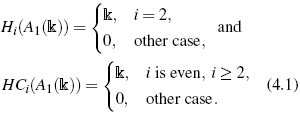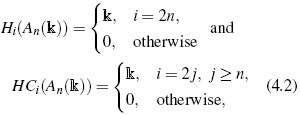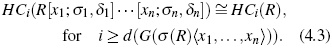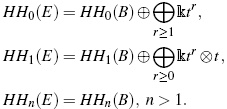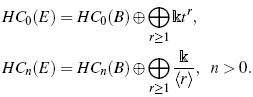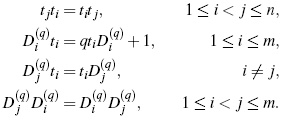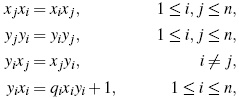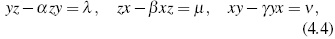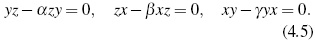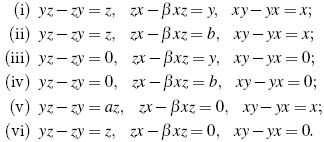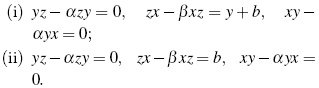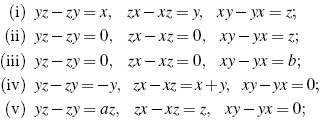Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ciencia en Desarrollo
Print version ISSN 0121-7488
Ciencia en Desarrollo vol.7 no.2 Tunja July/Dec. 2016
Some Remarks About the Cyclic Homology of Skew PBW Extensions
Algunas observaciones sobre la homología cíclica de extensiones PBW torcidas
Milton Armando Reyes Villamila*
Héctor Julio Suárez Suárezb
a Seminario de Álgebra Constructiva -SAC2, Departamento de Matemáticas, Universidad Nacional de Colombia -sede Bogotá, Colombia.
* Correo electrónico: mareyesv@unal.edu.co
b Escuela de Matemáticas y Estadística, Universidad Pedagógica y Tecnológica de Colombia, Tunja, Boyacá, Colombia.
Recepción: 11-feb-2016 Aceptación: 29-may-2016
Abstract
We study the cyclic homology for a class of noncommutative polynomial rings known as skew PBW extensions. We obtain explicit computations for some important families of such extensions over fields. In particular, we consider the cyclic homology of skew PBW extensions of derivation type, certain classes of Ore extensions, operator algebras, difusion algebras, quantum algebras and 3-dimensional skew polynomial algebras.
Key words: Cyclic homology, Filtered rings, Skew PBW extensions.
Resumen
Estudiamos la homología cíclica de una clase de anillos de polinomios no conmutativos denominados extensiones PBW torcidas. Obtenemos cálculos explícitos para algunas familias importantes de este tipo de extensiones sobre cuerpos. En particular, consideramos la homología cíclica de las extensiones PBW torcidas de tipo derivación, ciertas clases de extensiones de Ore, álgebras de operadores, álgebras de difusión, álgebras cuánticas y álgebras de polinomios torcidos 3-dimensionales.
Palabras clave: Anillos filtrados, Extensiones PBW torcidas, Homología cíclica.
1. Introduction
Cyclic homology of algebras was discovered by Connes in the formulation of noncommutative differential geometry [3]. In connection with the pairing with algebraic or topological K-theory, cyclic homology is quite useful also for the study of K theory. For instance, Connes uses cyclic cocycles to express certain characteristic classes of a foliation in connection with the topological K-theory of the associated foliation C∗-algebra. In this context, it seems to be important to compute cyclic cohomology of interesting algebras, which appear in differential topology or in algebraic geometry. Cyclic homology has been studied in a series of papers as a non-commutative generalization of de Rham cohomology (cf. [14], [23], [4], [5]) in order to interpret index theorems for non-commutative Banach algebras, via a generalization of the Chern character, where it was shown in [3] that cyclic homology of C∞(M) recovers the C-coefficient de Rham homology of the compact smooth manifold M. Cyclic homology was also shown to be the primitive part of the Lie algebra homology of matrices by Quillen and Loday [14]. This relationship shows that cyclic homology can be considered as a Lie analogue of algebraic K-theory and it is sometimes referred to as non-commutative differential geometry. Following [15], the cyclic homology of an k-algebra B (k being a commutative ring) consists of abelian groups HCn(B), n ≥ 0. If k is a field with characteristic zero, these groups are the homology groups of the quotient of the Hochschild complex by the action of the finite cyclic groups; this is the reason for the term "cyclic". The notation HC was for "Homologie de Connes", but soon became "Homologie Cyclique".
Since we are interested in computing the cyclic homology groups of skew PBW (PBW denotes Poincaré-Birkhoff-Witt) extensions introduced in [7], in this paper we have compiled some facts about these groups for certain examples of this kind of extensions. We consider that this study enriches the study of non-commutative differential geometry of a considerable number of noncommutative rings and quantum groups (for instance, quantum spaces whose cyclic homologies were known [4], quasicommutative algebras [11], Q-difference operators [9], Ore extensions and some quantum algebras [10]). The techniques used here are fairly standard and follow the same path as other text on the subject. The results presented are new for skew PBW extensions and all they are similar to others existing in the literature. In this way, we continue the task of studying several properties of skew PBW extensions and its relationship with other noncommutative rings (see [1], [8], [12], [13], [17], [18], [19], [20], [22], [24] and others).
The paper is organized as follows. In Section 2 we describe the skew PBW extensions. In Section 3 we recall the higher algebraic K-theory of these extensions following [13], and then we present the key results of this paper concerning about cyclic homology of these rings. Finally, in Section 4 we illustrate the results about cyclic homology of Section 3 with several examples such as Ore extensions, diffusion algebras, operator algebras and 3-dimensional skew polynomial algebras.
2. Skew PBW Extensions
Definition 1 ([7], Definition 1). Let R and A be rings. We say that A is a skew PBW extension of R (also called a σ-PBW extension of R) if the following conditions hold:
(i) R ⊆ A.
(ii) There exist finite elements x1,...,xn ∈ A such A is a left R-free module with basis
Mon(A) := {xα = xα1·xnαn&124; α =
(α1,...,αn) ∈ Nn}.
We say also that A is a left polynomial ring over R with respect to the set of variables {x1,...,xn}and Mon(A) is the set of standard monomials of A. In addition, x10 ···xn := 1 ∈ Mon(A).
(iii) For every 1 ≤ i ≤ n and r ∈ R \{0} there exists ci,r ∈ R \{0} such that xir − ci,rxi ∈ R.
(iv) For every 1 ≤ i, j ≤ n there exists ci, j ∈ R \{0}such that xjxi − ci, jxixj ∈ R + Rx1 + ··· + Rxn.
Under these conditions we will write A := σ(R)x1,...,xn.
The following proposition justifies the notation for skew PBW extensions. Before, we recall the notion of skew polynomial ring. If B is a ring and σ is a ring endomorphism σ : B → B,a σ-derivation δ : B → B satisfies by definition δ(r + s)= δ(r)+ δ(s), and δ(rs)= σ(r)δ(s)+ δ(r)s for all r,s ∈ B. If y is an indeterminate, and yb = σ(b)y + δ(b), for any b ∈ B, we denote this noncommutative ring as B[y;σ,δ] which is called a skew polynomial ring.
Proposition 2 ([7], Proposition 3). LetA be askew PBW extension of R. Then, for every 1 ≤ i ≤ n, there exist an injective ring endomorphism σi : R → R and a σi-derivation δi : R → R such that xir = σi(r)xi + δi(r) for each r ∈ R.
Definition 3. Let A be a skew PBW extension.
- ([7], Definition 4.) A is quasi-commutative if the conditions (iii) and (iv) in Definition 1 are replaced by
- A is bijective if σi is bijective for every 1 ≤ i ≤ n and ci, j is invertible for any 1 ≤ i < j ≤ n.
- ([12], Definition 2.3.) A is a skew PBW extension of derivation type if σi = idR for 1 ≤ i ≤ n.
(iii') For every 1 ≤ i ≤ n and r ∈ R \{0} there exists ci,r ∈ R \{0} such that xir = ci,rxi.
(iv') For every 1 ≤ i, j ≤ n there exists ci, j ∈ R \{0} such that xjxi = ci, jxixj.
Definition 4. A filtered ring is a ring B with a family FB = {FnB &124; n ∈ Z} of additive subgroups of B where we have the ascending chain ··· ⊂ Fn−1B ⊂ FnB ⊂ ··· such that 1 ∈ F0B and FnBFmB ⊆ Fn+mB for all n,m ∈ Z. From a filtered ring B it is possible to construct its associated graded ring G (B) taking G (B)n := FnB/Fn−1B.
The next proposition computes the graduation of a general skew PBW extension of a ring R. This result will very important in Proposition 12.
Proposition 5 ([13], Theorem 2.2). Let A be an arbitrary skew PBW extension of R. Then, A is a filtered ring with increasing filtration given by
and the corresponding graded ring G(A) is a quasicommutative skew PBW extension of R. Moreover, if A is bijective, then G(A) is a quasi-commutative bijective skew PBW extension of R.
Remark 6. The associated graded ring G(A) is the skew PBW extension of R generated by the variables z1,...,zn with the relations zir = ci,rzi, zjzi = ci, jzizj, for 1 ≤ i ≤ n, where ci,r,ci, j are the same constants that define A. See [13], Proposition 2.1 for a proof of this assertion.
Proposition 7 establishes the relation between skew PBW extensions and iterated skew polynomial rings in the sense of Proposition 2.
Proposition 7 ([13], Theorem 2.3). Let A be a quasicommutative skew PBW extension of a ring R. Then (i) A is isomorphic to an iterated skew polynomial ring, and (ii) if A is bijective, each endomorphism of the skew polynomial ring in (i) is an isomorphism.
3. Algebraic K-Theory and Lie Analogue of Higher Algebraic K-Theory
As we said in the Introduction, cyclic homology was shown to be the primitive part of the Lie algebra homology of matrices by Quillen and Loday [14]. This relationship shows that cyclic homology can be considered as a Lie analogue of algebraic K-theory and it is sometimes referred to as non-commutative differential geometry. With this in mind, in the first part of this section we recall the higher algebraic K-theory of skew PBW extensions following [13], while the second part treats with the cyclic homology of skew PBW extensions.
3.1. Higher Algebraic K-Theory of Skew PBW Extensions
Quillen [16] proposed defining the higher algebraic K-theory of a ring B to be the homotopy groups of a certain topological space which he called "BGL(R)+". In fact, he provided two fundamentally different ways of defining higher algebraic K-groups, one homotopy theoretic and the other category theoretic. Following a categoric treatment, Lezama and Reyes [13] computed the higher algebraic K-theory of bijective skew PBW extensions.
Proposition 8 ([13], Theorem 5.1). Let R be a left Noetherian left regular ring. If A is a bijective skew PBW extension of R, then Ki(A) ≈ = Ki(R) for all i ≥ 0.
With this result, it is possible to obtain the Quillen's groups Ki,i ≥ 0 for several families of noncommutative rings which are examples of bijective skew PBW extensions. For instance, PBW extensions, Ore extensions of bijective type, operator algebras, diffusion algebras, some quantum algebras, and 3-dimensional skew polynomial algebras, and some localizations of skew PBW extensions (see [13] for a detailed reference of every family). A detailed list of these groups can be found it in [13].
3.2. Lie Analogue of Higher Algebraic K-Theory of Skew PBW Extensions
We recall the definitions of Hochschild and cyclic homology following [6]. For more details see [4], [5], [14], [15] or [23].
Definition 9. Let B be an associative algebra over a commutative unital ring k, k ⊂ B. The Hochschild homology of B, denoted by HH∗(B), is defined to be the homology of the following complex
where Cn(B)= B⊗n +1 , and d : Cn(B) →Cn−1(B) such that
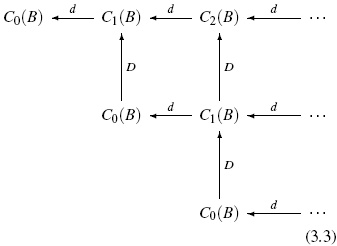
The cyclic homology of B, denoted by HC∗(B), is defined to be the total homology of the following double complex
where D : Cn(B)→ Cn +1 (B) such that
In [2] Hochschild homology and cyclic homology are denoted by Hi(B;B) and HCi(B), respectively. The Hochschild homology dimension of an algebra is established in the next definition.
Definition 10 ([2], Definition 3.1). Let B be an algebra. Let d (A) = inf{n ∈ Z0 &124; Hi (B;B) = 0 for i > n}. The value d (B) is called the Hochschild dimension of B.
Proposition 11 ( [2], Theorem 3.4 ). Let B be an algebra with an increasing filtration FB = {FpB &124;F−1B = 0, p ∈ Z}. Suppose that d (G (B)) = n < ∞. Then the natural map HCi (F0B) → HCi(B) is an isomorphism for all i ≥ n.
The key result of this paper is Proposition 12 which establishes the cyclic homology of skew PBW extensions.
Proposition 12. Let R bearing. If A is a skew PBW extension of R and d (G (A)) < ∞, then HCi (A) ≈ = HCi (R) for all i ≥ d (G (A)).
Proof. The result follows from Proposition 5 and Proposition 11.
The following example will be of great importance in the Section 4.
Example 13. Let k be a field, Q =(qi, j)1≤i, j≤v a family of elements of k \ {0} verifying qi,i = 1 and qi, jqj,i = 1 for all i < j, and X = {x1,...,xv} a set of v indeterminates. The multiparametric affine space is the k-algebra SQ(X) generated by x1,...,xv and the relations xjxi = qi, jxixj,1 ≤ i < j ≤ v. Note that SQ(X)= σ(k)x1,...,xv.
When all the coefficients qi, j for i < j are equal to a constant q, the Hochschild dimension of SQ(X) is equal to v if q is a root of unity, and it is equal to 1 if q is not a root of unity ([10], Remark 3.1.1). In the general case we have
(i) HHn(SQ(X)) = 0 for all n > v;
(ii) If HHn(SQ(X)) = 0, then HHm(SQ(X)) = 0 for all m ≤ n.
(iii) The Hochschild dimension of SQ(X) is the greatest n such that there exist indexes 1 ≤ p1 < ··· < pn ≤ v and a family of natural members mpi ,1 ≤ i ≤ n verifying
(see [10], Corollary 3.1.4 for more details).
Remark 6, Proposition 12 and Example 13 guarantee the following result
Proposition 14. Let A be a skew PBW extension of type derivation over a field k. Then HCi(A) ≈ = HCi(k) for i ≥ d(SQ(X)).
4. Examples
In this section we present examples of skew PBW extensions where Proposition 12 and Proposition 14 can be applied. The complete references of all examples can be found in [13].
4.1. PBW Extensions
Any PBW extension A = σ(R)x1,...,xn is a bijective skew PBW extension since in this case σi = idR for every 1 ≤ i ≤ n, and ci, j = 1 for every 1 ≤ i, j ≤ n. Thus, for PBW extensions we have A = idR (R) x1,...,xn. Some particular examples of PBW extensions are the polynomial rings, skew polynomial rings of derivation type, universal enveloping algebras, and differential operator rings.
We recall that a filtered algebra B is called quasicommutative if its associated graded algebra is commutative. This is the case for PBW extensions above, which follows from Proposition 5. The Hochschild homology and the cyclic homology of this type of algebras was computed in [11].
Example 15.
- ([15], p. 10, 59). For a commutative ring k, HH0(k)= k and HHn(k)= 0, n > 0. With respect to the cyclic homology, HC2n(k)= k, HC2n+1(k)= 0, n ≥ 0.
- Let U (g) be the universal enveloping algebra of a Lie algebra g of dimension n over a field k of characteristic 0. Since G(U (g)) is isomorphic to a polynomial ring k[x1,...,xn], and d(k[x1,...,xn]) = n, then HCi(U (g)) ≈HCi(k) for i ≥ n.
- For any Lie algebra g, Kassel [11] computed the Hochschild and cyclic homology groups of its enveloping algebra in terms of the canonical Lie-Poisson structure on the dual g*. For the first Weyl algebra, Kassel proves that if k is a field of characteristic zero, then Since A1(k) ≈= σ(k[x])y, we have G(A1(k)) = k[x,y] and d(G(A1(k))) = 2. Hence, Proposition 12 implies HCi(A1(k)) = HCi(k), i ≥ 2, which coincides with (4.1) and [15], p. 10, 59.
- Loday [15], p. 94, showed that for a field k containing the field of rational numbers Q, the Hochschild homology and the cyclic homology of the Weyl algebra An(k), are given by respectively. Since An(k) ≈σ(k[x1,...,xn]) = y1,...,yn ([13], Section 3.1), then G(An(k)) ≈ = k[x1,...,xn,y1,...,yn]. In this way d(G(An(k))) = 2n, and by Proposition 12 we obtain HCi(An(k)) = HCi(k[x1,...,xn]), i ≥ 2n, which coincides with (4.2).
- With respect to universal enveloping algebras, Kassel [11] computed its Hochschild homology and cyclic homology. He obtain exact values for the groups Hi (U (sl (2,k))), HCi(U (s l(2,k))), Hi (U (so(4))), and HCi (U (so (4))), i ≥ 0.
4.2. Ore Extensions of Bijective Type
Any skew polynomial ring R[x;σ,δ] of bijective type (σ bijective) is a bijective skew PBW extension. In this case we have R[x;σ,δ] ≈If additionally δ = 0, then R[x;σ] is quasi-commutative. In a general way, let R [x1;σ1,δ1]···[xn;σn,δn] be an iterated skew polynomial ring of bijective type, i.e., the following conditions hold:
- for 1 ≤ i ≤ n, σi is bijective;
- for every r ∈ R and 1 ≤ i ≤ n, σi(r),δi(r) ∈ R; for i < j, σj(xi)= cxi + d, with c,d ∈ R and c has a left inverse;
- for i < j, δj(xi) ∈ R + Rx1 + ··· + Rxn,
then, R[x1;σ1,δ1]···[xn;σn,δn] is a bijective skew PBW extension. Under these conditions we have R[x1;σ1,δ1]··· [xn;σn,δn] ≈ = σ (R) x1,...,xn ( [13], Section 3.2). Therefore, by Remark 6 we have G(σ (R) x1,...,xn ) ≈R [z1;σz1··[zn;σzn ], where =]·σj (r)= cj,r and σj (zi) = ci, jzi for 1 ≤ i < j ≤ n. By Proposition 12 we obtain
Example 16. Some remarkable examples of this kind of noncommutative rings are the following:
- Quantum plane Oq (k2). Let q ∈ k \{0}. The quantized coordinate ring of k2 isa k-algebra, denoted by Oq (k2), presented by two generators x,y and the relation xy = qyx. We have Oq(k2) ≈= k [y] [x;σx]. = σ (k) x,y, G (Oq (k2)) ≈If q is a root of the unity, HCi (Oq (k2)) ≈ = HCi (k) for i ≥ 2, and if q is not a root of the unity, HCi (Oq(k2)) ≈ = HCi (k) for i ≥ 1.
- The algebra of q-differential operators Dq, h [x,y]. Let q, h ∈ k, q ≠ 0; consider the = ring k[y] [x; σx,δ ], where σx (y) := qy, δ(y) := h. Then xy = σx (y) x + δ (y)= qyx + h whence xy − qyx = h, and hence Dq,h [x,y] ≈ = σ (k) x,y. In this way G (Dq,h [x,y] ) ≈ = k [y] [x;σx]. Again, if q is a root of the unity, then HCi ( Dq,h[x,y] ) ≈ = HCi (k) when i ≥ 2, and if q is not a root of the unity, HCi (Dq,h [x,y] ) ≈ = HCi (k) when i ≥ 1.
- The mixed algebra Dh. It is defined by d Dh := k[t] [x;idk [t],
dt][xh;σh], where h ∈ k and σh (x) := x. Then Dh = σ (k) t,x,xh, G (Dh) ≈ = k [t] [x;idk [t]] [xh;σh]. If q is a root of the unity, HCi(Dh) ≈In other case, = HCi (k) for i ≥ 3. HCi(Dh) ≈ = HCi(k) for i ≥ 1.
Remark 17. Guccione and Guccione in [10] computed under certain conditions the Hochschild homology and the cyclic homology of Ore extensions. For instance, they proved ([10], Corollary 2.5) that if kis a field, B a k-algebra and E = B[t;α,δ] an Ore extension satisfying the following conditions:
- Asa k-module, B is a direct sum B = s∈Nv Bs, with B0 = k,
- There exist q1,...,qv ∈ k\{0} such that α−1(a) = qm11···qmvva, provided that a ∈ B (m1,...,mv), and if q1m1···qmv v = 1 implies m1 = ··· = mv = 0, then the Hochschild homology of E with coefficients in E is given by
The cyclic homology of E is given by
4.3. Operator Algebras
In this subsection we recall some important and well-known operator algebras. Some of these algebras are skew PBW extensions of fields and hence we can apply the result established in (4.3).
- Algebra of linear partial differential operators. The nth Weyl algebra An(k) over k coincides with the k-algebra of linear partial differential operators with polynomial coefficients k[t1,...,tn]. As we have seen, the generators of An(k) satisfy the following relations titj = tjti, ∂i∂j = ∂j∂i, for 1 ≤ i < j ≤ n, and ∂jti = ti∂j + δij, for 1 ≤ i, j ≤ n, where δij is the Kronecker symbol. Therefore σ(k)t1,...,tn;∂1,...,∂n, its associated graded ring is isomorphic to k[t1,...,tn;∂1,...,∂n] and HCi(σ (k) t1,...,tn;∂1,...,∂n) ≈ = HCi(k), for i ≥ 2n.
- Algebra of linear partial q-differential operators. For a fixed q ∈ k \{0}, this is the kalgebra k[t1,...,tn][D(q) ,...,D(q)], n ≥ m, subject to the relations:
- Operator differential rings. Let R be an algebra over a commutative ring k and let Δ = {δ1,...,δn} be a set of commuting derivations of R. Let T = R [θ1,...,θn;δ1,...,δn] be the operator differential ring. The elements of T can be written in a unique way as left R-linear combinations with the ordered monomials in θ1,...,θn. The product on T is defined extending the product from R subject to the relation θir − rθi = δi (r), r ∈ R, i = 1,...,n, and θiθj − θjθi = 0, i, j = 1,...,n, and T = σ (R) θ1,...,θn. Then HCi (T )= HCi(R) for i ≥ n.
If n = m, this operator algebra coincides with the additive analogue An (q1,...,qn) of the Weyl algebra An(q) (Section 4.5, Example (a)). This algebra can be expressed as the skew PBW extension σ(k)t1,...,tn;D(q),...,Dm (q), and hence HCi (σ (k) t1,...,tn; D(q),...,D m(q)))= ≈ HCi (k), i ≥ n + m.
4.4. Diffusion Algebras
Diffusion algebras arose in physics as a possible way to understand a large class of 1-dimensional stochastic process. A diffusion algebra A with parameters ai j ∈ C\{0},1 ≤ i, j ≤ n is a C-algebra generated by indeterminates x1,...,xn subject to relations ai jxixj − bi jxjxi = rjxi − rixj, whenever i < j, bij,ri ∈ C for all i < j. Therefore A admits a PBW -basis of standard monomials x1 i1 ···xn in, that is, A is a diffusion algebra if these standard monomials are a C-vector space basis for A . From Definition 1, (iii) and (iv), it is clear that the family of skew PBW extensions are more general than diffusion algebras.
In the applications to physics the parameters aij are strictly positive reals and the parameters bij are positive reals as they are unnormalised measures of probability. We will denote 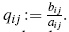 . The parameter qij is a root of unity if and only if is equal to 1. It is therefore reasonable that we will sometimes assume these parameters not to be a root of unity other than 1. If all coefficients qi j are nonzero, then the corresponding diffusion algebra have a PBW basis of standard monomials xi11···xinn and hence these algebras are skew PBW extensions, but not Ore extensions (see [13]). Therefore, HCi(A) = HCi(C) for i ≥ d(G (A)).
. The parameter qij is a root of unity if and only if is equal to 1. It is therefore reasonable that we will sometimes assume these parameters not to be a root of unity other than 1. If all coefficients qi j are nonzero, then the corresponding diffusion algebra have a PBW basis of standard monomials xi11···xinn and hence these algebras are skew PBW extensions, but not Ore extensions (see [13]). Therefore, HCi(A) = HCi(C) for i ≥ d(G (A)).
4.5. Quantum Algebras
The term quantum group is usually used, not only for the q-analogue of the coordinate ring of a semisimple algebraic group but also for the qanalogue of the universal enveloping algebra of a semisimple Lie algebra. A quantum group is a Hopf algebra but in this article we will only concerned with the algebra structure and so the coalgebra structure will not be considered. We remark that the exact value of the Hochschild dimension of the associated graded ring of every skew PBW extension A, that is, d(G(A)) can be found it using Example 13.
Example 18.
- Additive analogue of the Weyl algebra. The k-algebra An(q1,...,qn) is generated by the variables x1,...,xn, y1,...,yn subject to the relations:
- Quantum algebra U (so(3,k)). This algebra is the q-analogue of the universal enveloping algebra so(3,k). By definition it is the k-algebra generated by the variables I1, I2, I3 subject to relations I2 I1 − qI1I2 = −q1/2 I3, I3I1 −q−1I1I3 = q−1/2I2, I3I2 −qI2I3 = −q1/2I1, where q ∈ k \{0}. We have U (so(3,k)) ≈ = σ(k)I1,I2,I3.
- Dispin algebra U (osp (1,2)). This algebra is generated by x,y,z over the commutative ring k satisfying the relations yz − zy = z, zx + xz = y, xy − yx = x. Thus, U (osp (1,2)) ≈ = σ(k)x,y,z.
- Woronowicz algebra W ν (sl(2,k)). This algebra is generated by x,y,z subject to the relations xz − ν4 zx =(1 + ν2) x, xy − ν2yx = νz, zy − ν4yz = (1 + ν2) y, where ν ∈ k − {0} is not a root of unity. Under certain conditions on ν we have the isomorphism W ν (sl(2,k)) ≈ = σ(k)x,y,z.
- q-Heisenberg algebra. The k-algebra Hn(q) is generated by the set of variables x1,...,xn, y1,...,yn, z1,...,zn subject to the relations:
where qi ∈ k \{0}. In this way we have An(q1,...,qn)= ≈ σ(k)x1,...,xn,y1,...,yn, that is, An(q1,...,qn) is a skew PBW extension of the field k.
4.6. 3-Dimensional Skew Polynomial Algebras
The universal enveloping algebra U (sl (2,k)) of the Lie algebra sl (2,k), the Woronowicz's algebra W ν (sl (2,k)) and the dispin algebra U (osp (1,2)), are examples of algebras classified by Smith and Bell which are known as 3-dimensional skew polynomial algebras. Next we recall the definition of this algebras and we will see that they are particular examples of skew PBW extensions.
Definition 19. A 3-dimensional skew polynomial algebra A is the k-algebra generated by the variables x,y,z restricted to relations
such that
- λ, µ,ν ∈ k+ kx + ky + kz, and α,β,γ ∈ k *;
- Standard monomials {xiyjzl&124; i, j,l ≥ 0} are a k-basis of the algebra.
It is clear from Definition 4.4 that 3-dimensional skew polynomial ring are skew PBW extensions of the field k. Hence, HCi(A )= HCi(k) for i ≥ d(G(A )).
Finally, we recall Proposition 20 which establishes a classification of 3-dimensional skew polynomial algebras.
Proposition 20 ([21], Theorem C.4.3.1, p. 101).
Let A be a 3-dimensional skew polynomial algebra. Then A is one of the following algebras:
- if &124;{α,β,γ}&124; = 3, then A is defined by
- if &124;{α,β,γ}&124; = 2 y β ≠ α = γ = 1, A is one of the following algebras:
- If &124;{α,β,γ}&124; = 2 and β ≠ = α = γ = 1, then A is one of the following algebras:
- If α = β = γ ≠ = 1, then A is the algebra
yz − αzy = a1x+ b1, zx − αxz = a2y + b2,
xy − αyx = a3z + b3. - If ai = 0,i = 1,2,3, all nonzero values of bi give isomorphic algebras.
- If α = β = γ = 1, A is isomorphic to one of the following algebras
Here a,b are any elements k. All nonzero values of b give isomorphic algebras.
In this case b is an arbitrary element of k. Again, any nonzero values of b given isomorphic algebras.
Parameters a, b ∈ k are arbitrary and all nonzero values of b generates isomorphic algebras.
References
[1] V. A. Artamonov, "Derivations of skew PBW extensions", Communications in Mathematics and Statistics, vol. 3, pp. 449-457, 2015. [ Links ]
[2] J. Block, "Cyclic Homology of Filtered Algebras", K-Theory, vol. 1, pp. 515-518, 1987. [ Links ]
[3] A. Connes, "Cohomologie Cyclique et Functeurs de Extn", C. R. Math. Acad. Sci. Paris, vol. 296, pp. 953-958, 1983. [ Links ]
[4] A. Connes, "Non-commutative Differential Geometry", Publ. Math. IHES, vol. 62, pp. 257-360, 1985. [ Links ]
[5] B.L. Feigin and B.L. Tsygan, "Additive K-Theory, in K-Theory: Arithmetic and Geometry", Lecture Notes in Math, vol. 1289, pp. 67-209, 1988. [ Links ]
[6] P. Feng and B. Tsygan, "Hochschild and Cyclic Homology of Quantum Groups", Commun. Math. Phys., vol. 140, pp. 481-521, 1991. [ Links ]
[7] C. Gallego and O. Lezama, "Gröbner Bases for Ideals of σ-PBW Extensions", Comm. Algebra, vol. 39, no. 1, pp. 50-75, 2011. [ Links ]
[8] N. R. González, Y. P. Suárez, "Ideales en el Anillo de Polinomios Torcidos R[x;σ,δ]", Ciencia en Desarrollo, vol. 5, no. 1, pp. 31-37, 2014. [ Links ]
[9] J.A. Guccione and J.J. Guccione, "Hochschild and Cyclic Homology of Q-difference Operators", J. Math. Sci. Univ. Tokyo, vol. 35, no. 3, pp. 413-422, 1995. [ Links ]
[10] J.A. Guccione and J.J. Guccione, "Hochschild and Cyclic Homology of Ore Extensions and Some Examples of Quantum Algebras", K-Theory, vol. 12, pp. 259-276, 1997. [ Links ]
[11] C. Kassel, "L'homologie Cyclique des Algèbres Enveloppantes", Invent. Math., vol. 91, pp. 221-251, 1988. [ Links ]
[12] O. Lezama, J.P. Acosta and A. Reyes, "Prime ideals of skew PBW extensions", Rev. Un. Mat. Argentina, vol. 56, no. 2, pp. 39-55, 2015. [ Links ]
[13] O. Lezama and A. Reyes, "Some Homological Properties of Skew PBW Extensions", Comm. Algebra, vol. 42, pp. 1200-1230, 2014. [ Links ]
[14] Loday, J.-L. and Quillen, D., "Homologie Cyclique et Homologie de L'Algèbre de Lie des Matrices", C. R. Math. Acad. Sci. Paris, vol. 296, pp. 295-297, 1983. [ Links ]
[15] J.-L. Loday, Cyclic Homology. Springer-Verlag, sec.edit., 1998. [ Links ]
[16] D. Quillen, "Higher Algebraic K-Theory, in Algebraic K-Theory", Lecture Notes in Math. vol. 341, Springer, Berlin 1973. [ Links ]
[17] A. Reyes, "Gelfand-Kirillov Dimension of Skew PBW Extensions", Rev. Col. Mat. vol. 47, no. 1, pp. 95-111, 2013. [ Links ]
[18] A. Reyes, "Uniform dimension over skew PBW extensions", Rev. Col. Mat., vol. 48, no. 1, pp. 79-96, 2014. [ Links ]
[19] A. Reyes, "Jacobson's conjecture and skew PBW extensions", Rev. Integr. Temas Mat, vol. 32, no. 2, 139-152, 2014. [ Links ]
[20] A. Reyes, "Skew PBW Extensions of Baer, quasi-Baer, p.p. and p.q.-rings", Rev. Integr. Temas Mat., vol. 33, no. 2, pp. 173-189, 2015. [ Links ]
[21] A. L. Rosenberg, "Non-commutative Algebraic Geometry and Representations of Quantized Algebras". Math. Appl., vol. 330. Kluwer Academic Publishers, 1995. [ Links ]
[22] H. Suárez, O. Lezama, A. Reyes, "Some relations between N-Koszul, Artin-Schelter regular and Calabi-Yau algebras with skew PBW extensions", Ciencia en Desarrollo, vol. 6, no. 2, pp. 205-213, 2015. [ Links ]
[23] B.L. Tsygan, "Homology of Matrix Lie-Algebras over Rings and Hochschild Homology", Uspekhi Mat. Nauk, vol. 38, pp. 217-218, 1983. [ Links ]
[24] C. Venegas, "Automorphisms for Skew PBW Extensions and Skew Quantum Polynomial Rings", Comm. Algebra, vol. 43, no. 5, pp. 1877-1897, 2015. [ Links ]