Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.74 n.153 Medellín set./dez. 2007
THE SUB-STRUCTURAL SYNTHESIS METHOD (SSM) ON A HEAT CONDUCTION PROBLEM
APLICACIÓN DEL MÉTODO DE SÍNTESIS SUBESTRUCTURAL (SSM) A UN PROBLEMA DE CONDUCCIÓN DE CALOR
JUAN FERNANDO RAMÍREZ PATIÑO
Departamento de Ingeniería Mecánica. Universidad Nacional de Colombia, Sede Medellín,jframirp@unalmed.edu.co
ALBEIRO ESPINOSA BEDOYA
Departamento de Ingeniería Mecánica. Universidad Nacional de Colombia, Sede Medellín
Recibido para revisión agosto 31 de 2006, Aceptado septiembre 14 de 2007, Versión final septiembre 21 de 2007
RESUMEN. En éste trabajo se presenta la aplicación del método de síntesis subestructural (SSM) basado en la teoría de Rayleigh-Ritz a un problema de ingeniería. Dicho problema es el análisis de conducción de calor unidimensional en sistemas bidimensionales formados por miembros unidimensionales. Para este problema de conducción de calor se obtienen los autovalores asociados y su convergencia. Las soluciones obtenidas con el MSS son comparadas con las asociadas a la versión h del método del elemento finito convencional (MEF). Los resultados obtenidos abren un nuevo panorama de investigación relacionado con determinar la influencia del orden de las ecuaciones diferenciales que rigen el problema sobre la precisión y velocidad de convergencia de la solución dada por las funciones de aproximación.
PALABRAS CLAVE: Método de Síntesis Subestructural, Método de Elementos Finitos, Conducción
ABSTRACT. In this paper, the application of the Substructural Synthesis Method (SSM) on an engineering problem is presented, based on the theory by Rayleigh-Ritz. This problem is the unidimensional heat conduction analysis on bidimensional systems made of unidimensional members. For this heat conduction problem the associated eigenvalues and their convergence are obtained. Solutions obtained with the SSM are compared to those associated to the h version of the conventional Finite Element Method (FEM). The results obtain opened a whole new panorama of investigation related with determinate the influence on the order of differential equations that ruled the problem about the precision and velocity of the convergence of the solution given by the approximation functions.
KEY WORDS: Substructural Synthesis Method, Finite Elements Method, Heat Conduction, Eigenvalues Problem.
1. INTRODUCTION
Substructural synthesis is a method conceived to dynamically modeling a complex structure by using a reduce Degrees Of Freedom (DOF). The concept of sub-structural synthesis can be attributed to Hurty (1960-1965) [1], [2], who inspired by the idea of sub-structures, developed a dynamical analysis method also known as synthesis of component modes. After Hurtys work, Hale and Meirovitch (1980) [3] and Meirovitch and Hale (1981) [4] establish that the synthesis of component modes method and all of its variants are fundamentally different forms of Rayleigh-Ritz method, this new methodology was named as sub-structural synthesis, in which a constraint process forces the individually modeled substructures to act like a fully joint structure.
Meirovitch and Kwak (1990) [5] during the analysis of simple members and for the purpose of improve convergence, introduce a new class of functions that were named quasi-comparison functions, these functions are a lineal combination of admissible functions;
Quasi-comparison functions besides satisfying geometric boundary conditions (GBC) are capable to approximate the natural boundary conditions (NBC) and the differential equation on the desired level. These new quasi-comparison functions are applied in the sub-structural synthesis method by Meirovitch and Kwak (1991) [6], and that is how its real effectiveness is shown.
In general, structures do not posses the characteristics for which Meirovitch and Kwak (1991) had developed the SSM. It is for this kind of structures that Morales (2000) [7] combines a kinematic process with a constraint generalizing the application of the SSM.
After Moraless work (2000), Zarzalejo (2001) [8] dynamically analyses three-dimensional structures. According to the excellent results showed by the sub-structural synthesis method in dynamical analysis [5], [7], [8], and the stability analysis in the solution of the eigenvalues problem associated with buckling presented by Ramírez (2002) [9], this investigation is meant to develop a formulation that allows to apply the SSM in another engineering area, heat conduction.
2. HEAT CONDUCTION GENERAL MODEL
For a structure as the one showed on Fig. 1, a methodology that allows to apply SSM in problems related to heat conduction will be developed.
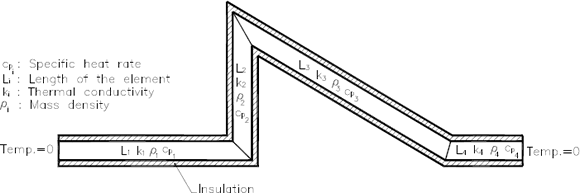
Figure 1: General model of heat conduction.
Figura 1: Modelo general de conducción de calor
Formulation for this problem is done under the following considerations:
- All the constituent elements of the structure have an equal and uniform straight section.
- The material of two consecutive substructures is different generally, but homogenous within a same element.
- An ideal isolation around all the elements will be considered.
- The dimensions of any cross section are considered small enough as to say that the temperature is constant in the section
- There is no internal heat generation.
- An initial condition of functional temperature exists, and it is different from zero.
- All the boundary conditions (BC) supposed are homogenous.
Using the previous considerations, it is possible to say that the outlined generic system is equivalent to the one shown in Fig. 2, where the elements can only be differentiated by the change in the material from a substructure to another one.

Figure 2: Equivalent model of heat conduction
Figura 2: Modelo equivalente de conducción de calor
For this heat conduction case, the totality of development in SSM made in the vibrations area is not applicable, in particular the Lagrangian formulation that allows to obtain the mass and stiffness matrices, then is necessary to define as departure point the partial differential equation that governs the heat conduction in one dimension, and then starting from this to determinate the eigenvalues problem associated as showed on Ec. (1).
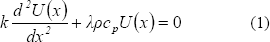
where:
U: Temperature
k: Thermal Conductivity
cp: Specific heat rate
r: Mass density
l: Associated eigenvalues.
To transform Ec (1) to a matrix from is necessary to outline the weak form of itself. In order to achieve this the weight function w is defined. Ec. (1) defines an eigenvalue problem, and multiplying it by the weight function the following is obtained:
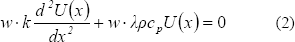
Integrating Ec. (2) by parts over the domain, the following is obtained:
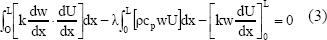
it represents the weak form of the equation that rules the heat conduction in one dimension. Expressing temperature U and weight function w in terms of approximation functions:
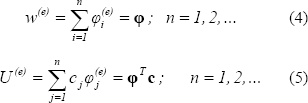
where is an admissible functions vector of different families and c is a vector of unknown coefficients, superscript (e) means that these approximations apply on each element and n is the approximation grade.
is an admissible functions vector of different families and c is a vector of unknown coefficients, superscript (e) means that these approximations apply on each element and n is the approximation grade.
Replacing the Ecs. (4) and (5) in Ec. (3) :
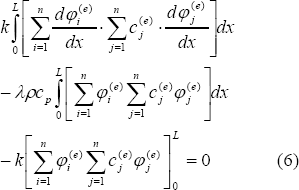
Here the first term represents the coefficients of the stiffness matrix, the second one the coefficients of the mass matrix, and the last one represents the BC of the eigenvalue problem [10]. Considering the solution of eigenvalue problems by means of the SSM, the GBC of the system are satisfied combining a correct selection of the approximation functions and a constraint process, and that approximation functions must also be able to approximate to the desired degree the NBC of the system, the last term of the Ec. (6) can be omitted in the formulation. Now under this simplification the Ec. (6) can be rewrite it as:
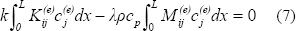
where:
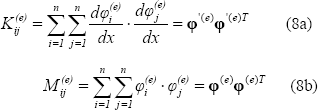
Clearly is seen that Ec. (7) can be written in a matrix form:
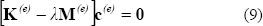
Ec. (9) defines the eigenvalue problem in matrix form for a constituent element or substructure and based on this equation write the eigenvalues problem in a matrix form in order to create a complete structure like the one shown one Fig. 1, the following is obtained:
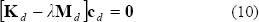
The matrices of the Ec. (10) can be transformed to the assembled system by using the constraint matrix C, which is generated when the compatibility of the temperature in the tie points of two contiguous substructures is guaranteed. Rewriting the Ec. (10) for the assembled system:

where:
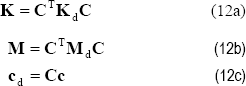
and C is the constraint matrix
2.1 Application To A Particular SystemThe detailed solution of the particular heat conduction problem by means of the SSM is showed next, the system appears in Fig 3.
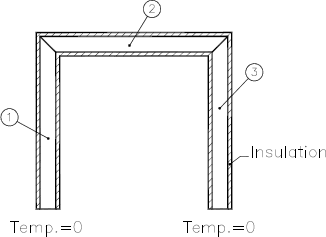
Figure 3: Particular structure for the analysis of heat conduction
Figura 3: Estructura particular para el análisis de conducción de calor
Equations (8a,b) defined the mass and stiffness matrix coefficients for a systems constituent element, in these equations it is necessary insert the approximation functions for each one of the substructures of the system.
Approximation functions. Solving the Ec.(1) under different boundary conditions is possible to obtain the approximation families that are going to be used and these appear in Table 1.Table 1: Approximation families
Tabla 1: Familias de aproximación
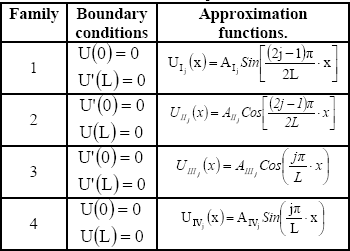
Where AI, ..., AIV are constants used to normalize the width of the approximation functions.
Approximation functions selection: Approximation functions selection is done based on Figure 4 and the BC offered by each one of the approximation families (Table 1), with which the functions vectors of the Ec. (8a, b) end up as showed in the Ecs. (13) and (14).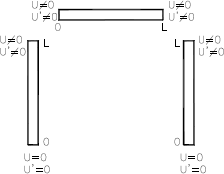
Figure 4: Boundary conditions of each substructure
Figura 4: Condiciones de borde de cada subestructura.
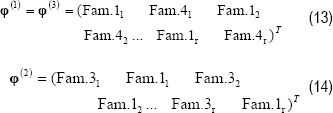
Inserting the Ecs. (13) and (14) in the Ecs. (8a, b), and all this as well in the Ec. (7), the eigenvalues problem of the disjoint system can be obtained as Ec. (10) shows. Now with the previously selected families the GBC in the starting points are satisfied automatically for substructures 1 and 3. In order to transform the eigenvalue problem of the disjoint system to the assembled one it is necessary to guarantee the compatibility in the temperature of the tie points of substructure 1 with the 2, and of substructure 2 with the 3. This can be done mathematically by means of the following equations
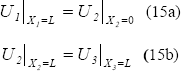
Introducing the Ec. (5) in the Ecs. (15a, b) and where the vectors 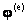 are based on the Ecs. (13) and (14), the constrain matrix C can be obtained, and as it shows the Ecs. (12a, b, c) transform the matrices from the disjoint system to the assembled one, thus to solve the eigenvalue problem associated to the heat conduction.
are based on the Ecs. (13) and (14), the constrain matrix C can be obtained, and as it shows the Ecs. (12a, b, c) transform the matrices from the disjoint system to the assembled one, thus to solve the eigenvalue problem associated to the heat conduction.
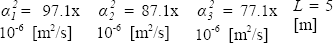
Where 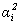 is thermal diffusivity for substructure i, calculated by:
is thermal diffusivity for substructure i, calculated by:

Eigenvalue problem is solved by means of the proposed SSM, in addition with the purpose of validating and comparing the obtained results it is also solved by means of the FEM using link elements with 1 DOF by node and polynomials of Lagrange like approximation functions. The convergence of the three first eigenvalues of the system, and for an equal precision up to five significant figures are showed in Table 2, where n represents the order of the involved matrices in eigenvalue problem and that is equivalent as well to the DOF of the assembled system.
Table 2: Convergence of the three first eigenvalues
Tabla 2: Convergencia de los tres primeros autovalores
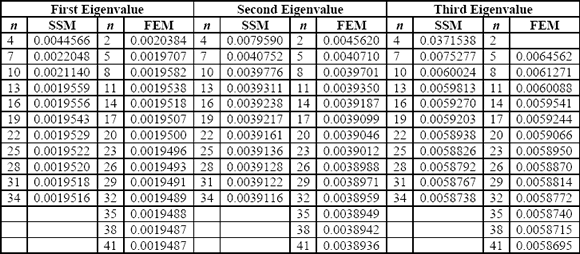
On Table 2 it is possible to see that for two first eigenvalues and the precision given, the solution obtained by means of the FEM presents characteristics of convergence superior to the ones showed by the SSM. Specifically for the first eigenvalue, by means of the FEM the convergence of five significant figures is reached with 38 DOF, whereas applying the SSM that level of precision is not possible to reach it with the approximation degree that allows the model (34 DOF), because from that point numerical problems appear, and that prevent to increase the DOF of the approximation. Considering that both methods of solution present a uniform convergence from above, for the second eigenvalue although neither methods reach the given precision, can be said that the eigenvalue found by means of the FEM with 38 DOF is more accurate to the actual eigenvalue that the presented one with 34 DOF by the SSM. Now for the third eigenvalue a very similar behavior in the approximation by means of both methods is notice, but the speed of convergence of the SSM, is minimally superior that the one of the FEM.
Because convergence problems exist, in particular the fact that it is not possible to go beyond of 34 DOF in the SSM approximation, a new group of approximation families will allow making a combination of three families by each substructure. For these new approximation functions a BC of radiating end will be considered and showed in Table 3.
Table 3: Approximation Families
Tabla 3: Familias de Aproximación

In families the from 5 to 7 a is a positive constant, and AV , AVI , AVII are constants that will allow to standardize the amplitude of the approximation functions. [11]
Considering the 7 approximation families available and not to violate the Homogeneous Geometric Boundary Condition (HGBC) other possible combinations were made, the one that threw better results is shown:
SSM1:
Substructures 1 and 3: Family 1 + Family 5 + Family 4.
Substructures 2: Family 3 + Family 1 + Family 2. a = 1
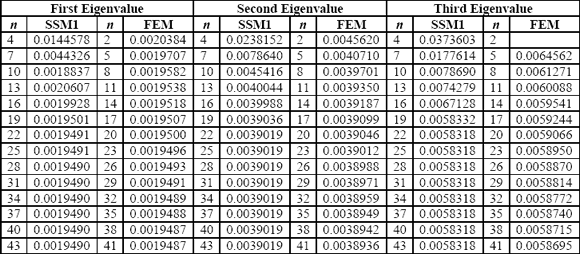
On Table 4 it is possible to see the combination of 3 families by each substructure in the SSM, not only allows to improve the convergence, but that also can increased the DOF, switching from 34 DOF in the previous combinations up to 43 DOF in this one. Specifically the convergence of the first eigenvalue for precision of five significant figures is reached by means of the FEM with 38 DOF, whereas applying the SSM this precision is not reached in the level of 43 DOF, is clearly possible to see that the convergence of the SSM stops in the same number since 28 DOF. Comparing the eigenvalues thrown by each one of the methods, the superiority of the SSM over the FEM is clearly seen.
Table 4: Convergence of the three first
Tabla 4: Convergencia de los tres primeros autovalores
3. CONCLUSIONS
The SSM can be applied in other areas of the engineering in which eigenvalue problems exist and can be solved.
The solution of the heat conduction eigenvalue problem by means of the SSM, although is viable because it throws values very near to those of the FEM, is not as efficient as in the case of vibrations or buckling, because in general FEM converges with a given precision to the eigenvalue using a smaller number of DOF for the approximation. This reduction of the convergence characteristics of the SSM in heat conduction can be attributed to the fact that heat problem is mathematically different from the dynamic problems (vibrations and buckling); additionally in the heat conduction model a kinematic process which help to increase the convergence speed of the method can not be applied.
REFERENCES
[1] HURTY, W.C. (1960),Vibrations of Structural ystems by Component-Mode Synthesis. Journal of the Engineering Mechanics Division , ASCE, Vol.86, pp.51-69. [ Links ]
[2] HURTY, W.C. (1965),Dynamic Analysis of Structural Systems Using Component Modes. AIAA Journal, Vol.3, No.4, pp.678-685. [ Links ]
[3] HALE, A.L., MEIROVITCH, L. (1980), A General Substructure Synthesis Method for the Dynamic Simulation of Complex Structures. Journal of Sound and Vibration, Vol.69, No.2, pp. 309-326. [ Links ]
[4] MEIROVITCH, L., HALE, A.L. (1981), On the Substructure Synthesis Method. AIAA Journal, Vol.19, No.7, pp. 940-947. [ Links ]
[5] MEIROVITCH, L., KWAK, M.K.,(1990), Convergence of the Classical Rayleigh-Ritz Method and the Finite Element Method. AIAA Journal, Vol.28, No.8, pp. 1509-1516. [ Links ]
[6] MEIROVITCH, L., KWAK, M.K.,(1991), Rayleigh-Ritz Based Substructure Synthesis Method for Flexible Multibody systems. AIAA Journal, Vol.29, No.10, pp. 1709-1519. [ Links ]
[7] MORALES, C.A. , (2000), Rayleigh-Ritz based substructure synthesis for multiply supported structures. Journal of Vibration and Acoustics, Vol22, pp. 2-6. [ Links ]
[8] ZARZALEJO, E.J. Análisis Dinámico de Estructuras en Tres Dimensiones Utilizando Síntesis Subestructural Basado en el Método de Rayleigh-Ritz. Tesis de Maestría. Universidad Simón Bolívar, Caracas – Venezuela, 2001. [ Links ]
[9] RAMÍREZ, J.F. Autosolución de Problemas de Pandeo y Conducción de Calor Mediante Síntesis Subestructural. Tesis de Maestría. Universidad Simón Bolívar, Caracas – Venezuela, 2002. [ Links ]
[10] REDDY J.N. An Introduction to the Finite Element Method. Mc Graw Hill, 1993. [ Links ]
[11] ONEIL, P.V. Matemáticas Avanzadas para Ingeniería. CECSA, 1994. [ Links ]














