Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.75 n.156 Medellín set./dez. 2008
CÁLCULO DE DERIVADAS EN ALGUNOS GRUPOS TOPOLÓGICOS
CALCULUS OF DERIVATIVES IN SOME TOPOLOGICAL GROUPS
HÉCTOR ANDRÉS GRANADA
Matemático, Universidad Nacional de Colombia, Sede Manizales, hagranadad@unal.edu.co
SIMEÓN CASANOVA TRUJILLO
Matemáticas, M.Sc, Profesor, Universidad Nacional de Colombia, Sede Manizales, scasanovat@unal.edu.co
Recibido para revisar septiembre 10 de 2007, aceptado Marzo 28 de 2008, versión final Julio 30 de 2008
RESUMEN: En este artículo se muestra a traves de ejemplos, la forma como se calculan derivadas en grupos topológicos. En cada uno de ellos se deben resolver ecuaciones diferenciales ordinarias o parciales.
PALABRAS CLAVE: Grupo topológico, homomorfismo, diferenciación en grupos topológicos.ABSTRACT: This article shows how to calculate derivatives in topological groups trough examples. In each of them one should solve ordinary or partial differential equations.
KEYWORDS: Topological group, homomorphism, differentiability in topological groups.
1. INTRODUCCIÓN
La derivada de Carathéodory para funciones 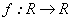 (
(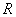 denota el conjunto de los números reales) le permitió a Acosta y Delgado generalizar esta a funciones
denota el conjunto de los números reales) le permitió a Acosta y Delgado generalizar esta a funciones 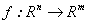 y mostrar su equivalencia con la derivada de Fréchet [1]. Con base en este último trabajo, Acosta generalizó la derivada de Carathéodory a grupos topológicos [2]. Tenemos así una forma de hacer cálculo diferencial en grupos topológicos. Sin embargo, en [2] no se muestra explícitamente un ejemplo en el que se calculen derivadas en grupos topológicos. En [3] se
y mostrar su equivalencia con la derivada de Fréchet [1]. Con base en este último trabajo, Acosta generalizó la derivada de Carathéodory a grupos topológicos [2]. Tenemos así una forma de hacer cálculo diferencial en grupos topológicos. Sin embargo, en [2] no se muestra explícitamente un ejemplo en el que se calculen derivadas en grupos topológicos. En [3] se
calculan derivadas para una función 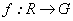 , donde
, donde 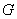 es un grupo que describiremos más adelante. En este artículo se retomará el trabajo hecho en [3] y se calcularán derivadas para funciones
es un grupo que describiremos más adelante. En este artículo se retomará el trabajo hecho en [3] y se calcularán derivadas para funciones 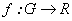 y
y 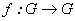 .
.
También se hará el cálculo de derivadas para un tipo particular de funciones 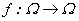 siendo
siendo 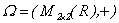 el grupo aditivo de las matrices de tamaño
el grupo aditivo de las matrices de tamaño 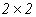 .
.
En general, el cálculo de derivadas en grupos topológicos conduce a la solución de ecuaciones diferenciales.
2. PRELIMINARES
En esta sección se presenta la definición de derivada en grupos topológicos dada en [2]. Para llegar a ella, se hace necesario los siguientes comentarios:
1. El espacio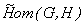 corresponde al conjunto de todos los homomorfismos continuos de
corresponde al conjunto de todos los homomorfismos continuos de 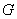 en
en 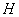 dotado de la topología compacto-abierta. Esta topología se describe como sigue:
dotado de la topología compacto-abierta. Esta topología se describe como sigue:
Sean 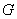 y
y 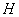 grupos topológicos Hausdorff. Si
grupos topológicos Hausdorff. Si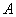 es un subconjunto compactode
es un subconjunto compactode 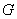 y
y 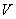 es un subconjunto abierto de
es un subconjunto abierto de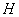 , se denota por
, se denota por 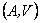 el conjuntode todas las funciones continuas
el conjuntode todas las funciones continuas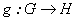 tales que
tales que 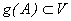 .
.
La topología compacto-abierta es la que tiene como sub-base la colección 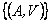 donde
donde 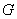 es localmente compacto.
es localmente compacto.
2. Un grupo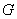 es divisible si para todo
es divisible si para todo 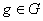 y
y 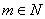 (
(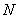 denota el conjunto de los números naturales), la ecuación
denota el conjunto de los números naturales), la ecuación 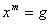 (en notación multiplicativa) tiene solución.
(en notación multiplicativa) tiene solución.
Definición 2.1. Sean 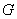 y
y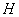 grupos topológicos Hausdorff. Una aplicación
grupos topológicos Hausdorff. Una aplicación 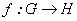 es diferenciable en
es diferenciable en 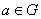 , si existe
, si existe 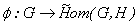 continua en
continua en 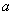 y tal que
y tal que
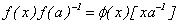
Si esta igualdad se da y 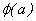 es única, la derivada de
es única, la derivada de 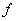 en
en 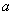 es
es 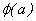 , y escribimos
, y escribimos 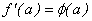 .
.
En la definición anterior, la igualdad debe ser válida en alguna vecindad del punto 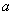 .
.
La operación del lado derecho es una evaluación y la notación es tomada de [2], pues es allí donde se da por primera vez una definición de derivada en grupos topológicos.
En [3] se dan condiciones suficientes para la unicidad de la derivada:
Sean 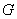 y
y 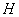 grupos topológicos Hausdorff,
grupos topológicos Hausdorff, 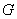 localmente compacto y divisible. Supóngase además que para todo
localmente compacto y divisible. Supóngase además que para todo 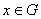 ,
, 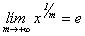 . Si
. Si 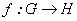 es diferenciable en
es diferenciable en 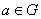 , entonces
, entonces 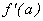 es única.
es única.
Se ve de la definición de derivada, que 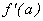 es un homomorfismo. Por lo tanto, para hacer cálculo diferencial en grupos topológicos, se debe empezar por calcular homomorfismos.
es un homomorfismo. Por lo tanto, para hacer cálculo diferencial en grupos topológicos, se debe empezar por calcular homomorfismos.
3. CÁLCULO DE HOMOMORFISMOS
En esta sección se hará el cálculo de ciertos homomorfismos, para usarlos en la próxima sección con el fin de calcular derivadas.
3.1 Consideremos el conjunto
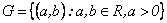
dotado de la ley de composición interna
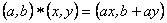
La dupla  es un grupo (no abeliano), donde el módulo es la pareja ordenada
es un grupo (no abeliano), donde el módulo es la pareja ordenada  y el
y el
inverso de  es
es 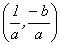 . Si se considera en
. Si se considera en 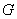 la topología inducida por la usual U de
la topología inducida por la usual U de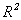 , se tiene que la tripla
, se tiene que la tripla 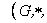 U
U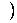 es un grupo topológico.
es un grupo topológico.
3.1.1 Homomorfismos de G en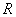
Sea 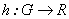 un homomorfismo. Entonces,
un homomorfismo. Entonces,
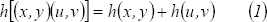
Se tiene además la condición inicial
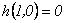 .
.
Como 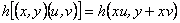
entonces de 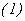 obtenemos que
obtenemos que
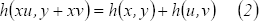
Haciendo 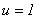 ,
, 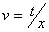 y usando la condición inicial en
y usando la condición inicial en 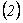 , se llega a:
, se llega a:
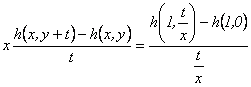
Tomando el límite cuando 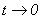 se tiene:
se tiene:
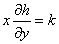
de donde
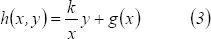
Derivando en esta última igualdad respecto a la variable 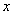 se obtiene:
se obtiene:
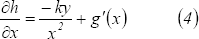
Ahora, en (2) se hace 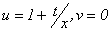 y obtenemos
y obtenemos

Tomando el límite cuando 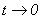 obtenemos:
obtenemos:

De 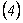 y
y 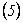 se llega a:
se llega a:
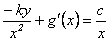
Para que esta última igualdad sea válida debe ser que 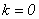 , de donde
, de donde
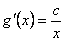
Así, 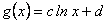 y en particular
y en particular 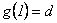 . De
. De 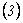 se tiene que
se tiene que
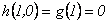
Luego, 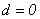 , o sea que
, o sea que 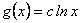 . Remplazando en
. Remplazando en 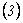 se llega a que los homomorfismos
se llega a que los homomorfismos 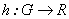 quedan caracterizados como:
quedan caracterizados como:
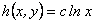
3.1.2 Homomorfismos de 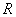 en G.
en G.
Sea 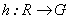 un homomorfismo. En primer lugar,
un homomorfismo. En primer lugar,
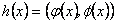 .
.
Ahora, como 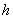 es homomorfismo entonces
es homomorfismo entonces
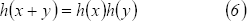
Por un lado se tiene que
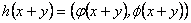
y por otro lado
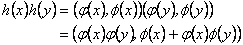
Remplazando las dos últimas relaciones en (6), se obtienen las siguientes relaciones funcionales:
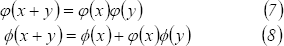
Como 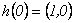 se tienen además las condiciones iniciales
se tienen además las condiciones iniciales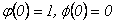 .
.
De (7) y las condiciones iniciales obtenemos
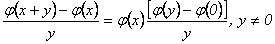
Tomando el límite cuando 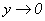 se llega a que
se llega a que 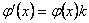 , de donde
, de donde 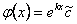 . De esta igualdad se sigue que
. De esta igualdad se sigue que 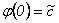 y usando las condiciones iniciales se tiene que
y usando las condiciones iniciales se tiene que 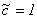 , así que
, así que

Ahora, de 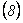 y
y 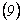 junto con las condiciones iniciales, se tiene que:
junto con las condiciones iniciales, se tiene que:
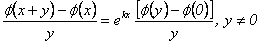
Tomando el límite cuando 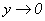 se obtiene
se obtiene 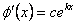 , de donde
, de donde 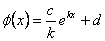 . De esta igualdad se sigue que
. De esta igualdad se sigue que 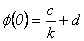 y usando las condiciones iniciales se llega a que
y usando las condiciones iniciales se llega a que 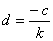 . Por lo tanto,
. Por lo tanto,
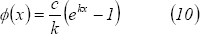
De (9) y (10) concluimos que los homomorfismos 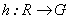 quedan caracterizados como:
quedan caracterizados como:
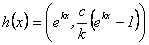
3.1.3 Homomorfismos de G en G. Sea 
Un homomorfismo. En primer lugar,
Como  es homomorfismo, entonces
es homomorfismo, entonces
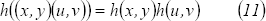
Por un lado
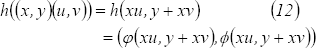
y por otro lado
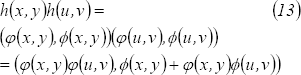
Remplazando  y
y 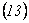 en
en  se obtienen las siguientes relaciones funcionales:
se obtienen las siguientes relaciones funcionales:
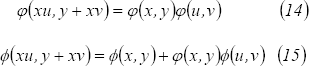
También, como 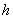 es homomorfismo se sigue que
es homomorfismo se sigue que 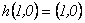 , de donde se tienen las condiciones iniciales
, de donde se tienen las condiciones iniciales
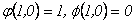 .
.
En (14) se hace 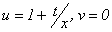 y se obtiene
y se obtiene
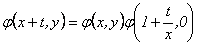
Usando las condiciones iniciales, se llega a:
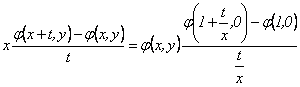
Tomando el límite cuando 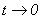 en esta última igualdad obtenemos la ecuación diferencial parcial
en esta última igualdad obtenemos la ecuación diferencial parcial
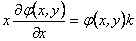
de donde
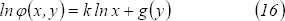
En esta igualdad derivamos respecto a 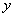 y se tiene:
y se tiene:
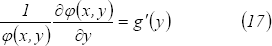
Usando nuevamente la relación  , hacemos
, hacemos 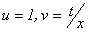 y se obtiene:
y se obtiene:

Tomando el límite cuando 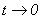 en esta última igualdad se llega a:
en esta última igualdad se llega a:
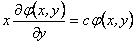
de donde
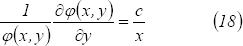
De  y
y  se tiene que
se tiene que 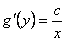 y para que esta igualdad tenga sentido, debe ser que
y para que esta igualdad tenga sentido, debe ser que 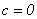 y de ahí que
y de ahí que 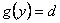 . Ahora, de
. Ahora, de  se tiene que
se tiene que
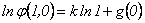
de donde 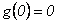 . Luego,
. Luego, 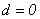 , es decir,
, es decir, 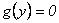 . De esta forma, de
. De esta forma, de  se sigue que
se sigue que

Para encontrar la función 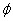 , en
, en 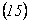 se hace
se hace 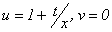 y razonando como antes se obtiene
y razonando como antes se obtiene
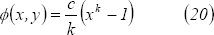
En conclusión, de  y
y  se tiene que los homomorfismos
se tiene que los homomorfismos 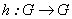 quedan caracterizados como:
quedan caracterizados como:
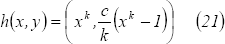
Se observa en los ejemplos que los homomorfismos encontrados dependen únicamente de la primera variable.
También en este ejemplo, se tiene que los homomorfismos de 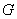 en
en 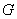 se obtienen realizando la composición de los homomorfismos de
se obtienen realizando la composición de los homomorfismos de 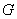 en
en 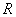 con los de
con los de 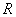 en
en 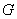 .
.
4. CÁLCULO DE DERIVADAS
4.1 Una vez hecho el cálculo de los homomorfismos 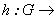
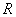 ,
, 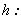
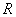
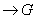 y
y 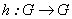 pasamos a calcular derivadas. El grupo
pasamos a calcular derivadas. El grupo 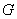 es localmente compacto y satisface las condiciones para que haya unicidad de la derivada (comentario 3 de los preliminares).
es localmente compacto y satisface las condiciones para que haya unicidad de la derivada (comentario 3 de los preliminares).
4.1.1 Derivada para funciones 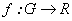
Veamos en primer lugar qué funciones 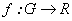 son diferenciables. Por la caracterización de los homomorfismos
son diferenciables. Por la caracterización de los homomorfismos 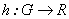 se tiene:
se tiene:

Haciendo 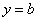 en esta igualdad se obtiene:
en esta igualdad se obtiene:

Como 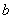 debe ser continua en
debe ser continua en  se tiene entonces que
se tiene entonces que

Se exige entonces que exista la derivada parcial de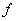 con respecto a
con respecto a 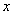 , evaluada en
, evaluada en 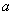 .
.
De esta manera, la derivada de 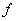 en
en  , evaluada en
, evaluada en 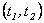 es :
es :
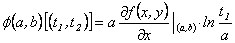
4.1.2 Derivada para funciones 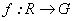
En primer lugar se debe ver qué funciones 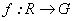 son diferenciables, es decir, para qué funciones
son diferenciables, es decir, para qué funciones 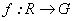 existe
existe 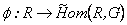 continua en
continua en 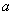 y tal que
y tal que
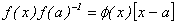
Tenemos que 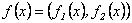 , siendo
, siendo 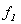 y
y 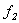 funciones de
funciones de 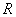 en
en 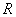 con
con 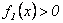 . Por un lado se tiene que
. Por un lado se tiene que
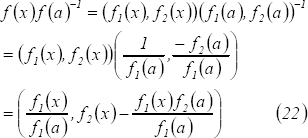
Por otra parte, teniendo en cuenta la caracterización de los homomorfismos de  en
en  , tenemos:
, tenemos:
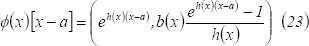
De (22) y (23) se obtienen las siguientes relaciones:
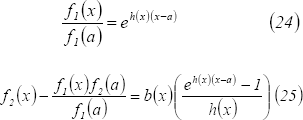
Al despejar 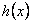 en
en  se llega a:
se llega a:
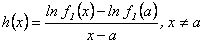
Como 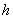 debe ser continua
debe ser continua 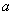 , entonces
, entonces
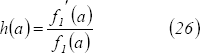
Se debe exigir entonces que 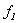 sea diferenciable en
sea diferenciable en 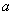 .
.
Ahora, de la ecuación  se tiene:
se tiene:
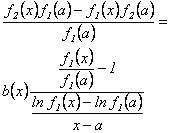
o bien,
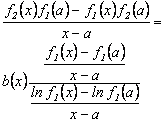
es decir,
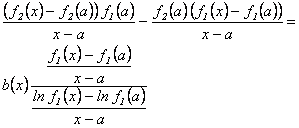
Como 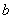 debe ser continua en
debe ser continua en 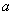 , entonces si en la anterior igualdad se toma el límite cuando
, entonces si en la anterior igualdad se toma el límite cuando 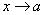 se tiene que:
se tiene que:
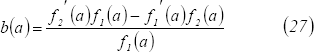
Se debe exigir entonces que 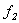 sea diferenciable en
sea diferenciable en 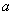 .
.
De (26) y (27) se tiene que la derivada de 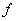 en
en 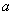 , evaluada en
, evaluada en 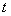 es:
es:
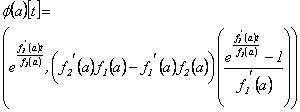
4.1.3 Derivada para funciones 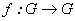
Como antes, veamos qué funciones 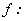
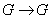 son diferenciables. Tenemos que
son diferenciables. Tenemos que
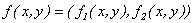
y por lo tanto,
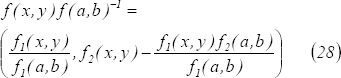
De otro lado, teniendo en cuenta la caracterización de los homomorfismos de 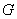 en
en  , se tiene que
, se tiene que
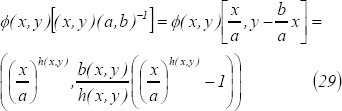
Igualando  y
y  se obtienen las siguientes ecuaciones:
se obtienen las siguientes ecuaciones:
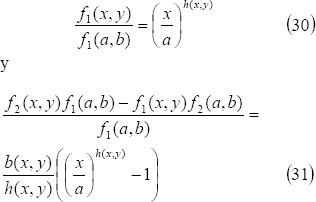
De  se llega a:
se llega a:
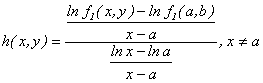
Haciendo 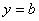 y teniendo en cuenta que
y teniendo en cuenta que 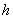 debe ser continua en
debe ser continua en  , entonces al tomar
, entonces al tomar 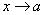 en la última igualdad, se obtiene que
en la última igualdad, se obtiene que
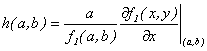
Ahora, de  se sigue que:
se sigue que:
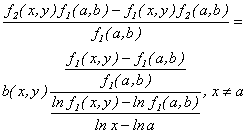
o bien,

Como 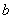 debe ser continua en
debe ser continua en  , entonces haciendo
, entonces haciendo 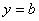 y tomando
y tomando 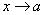 en la última igualdad, se tiene que:
en la última igualdad, se tiene que:
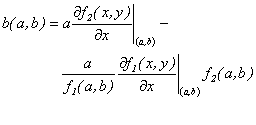
De esta manera, la derivada de  en
en  , evaluada en
, evaluada en  es
es
Donde 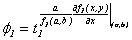 y
y
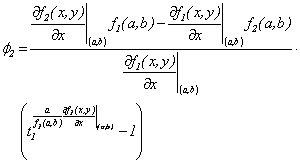
4.2 En esta sección se considerará el grupo topológico aditivo 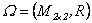 de las matrices cuadradas de tamaño
de las matrices cuadradas de tamaño 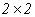 con entradas reales, el cual es localmente compacto, divisible y satisface las condiciones para la unicidad de derivada. En efecto, la divisibilidad se sigue del siguiente hecho: como estamos considerando
con entradas reales, el cual es localmente compacto, divisible y satisface las condiciones para la unicidad de derivada. En efecto, la divisibilidad se sigue del siguiente hecho: como estamos considerando 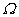 como grupo aditivo la divisibilidad significa que dado
como grupo aditivo la divisibilidad significa que dado 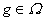 y
y 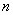 natural, existe
natural, existe 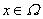 tal que
tal que 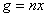 , lo cual en nuestro caso se tiene. Vale además que
, lo cual en nuestro caso se tiene. Vale además que 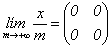 para todo
para todo 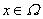 . La compacidad local de
. La compacidad local de  se sigue al ver
se sigue al ver 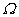 como
como 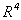 .
.
Definimos 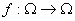 como:
como:
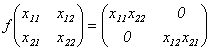
Se mostrará que esta función es diferenciable en cada 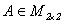 . En [4] se demuestra que los homomorfismos de
. En [4] se demuestra que los homomorfismos de 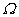 en
en 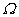 quedan caracterizados como:
quedan caracterizados como:
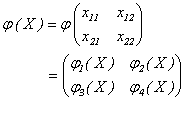
Donde
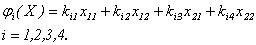
Debido a la linealidad de las 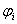 , se tiene que el homomorfismo
, se tiene que el homomorfismo 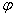 es continuo con la topología inducida por la de
es continuo con la topología inducida por la de 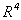 .
.
Definamos 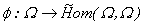 como:
como:
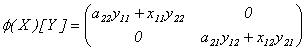
Con relación a esta definición, tenemos que efectivamente 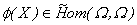 y que considerando en
y que considerando en 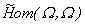 la topología compacto abierta, la aplicación
la topología compacto abierta, la aplicación 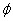 es continua en
es continua en 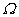 . Además,
. Además,
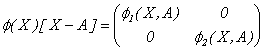
Donde
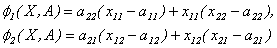
Se tiene así que
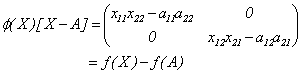
Por lo tanto, 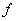 es diferenciable en
es diferenciable en 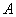 y
y
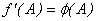
Donde
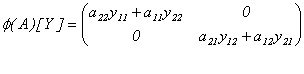
5. AGRADECIMIENTOS
Los autores expresan sus agradecimientos a los jurados del artículo por sus acertados comentarios, los cuales permitieron mejorar su presentación.
REFERENCIAS
[1] ACOSTA G. ERNESTO, DELGADO CÉSAR. Fréchet vs. Carathédory. American Mathematical Monthly, April 1994. [ Links ]
[2] ACOSTA G. ERNESTO. Differentiability in Topological Groups. Soochow Journal of Mathematics, Volume 22, No.1, pp 39-48. January 1996. [ Links ]
[3] CASANOVA T. SIMEÓN. Teorema del Valor Medio en Grupos Topológicos. Tesis de Maestría en Matemáticas. U.Nal. de Colombia, 1997. [ Links ]
[4] GRANADA D. HÉCTOR. Diferenciación en grupos metrizables. Tesis de grado en Matemáticas. U.Nal. de Colombia, Sede Manizales. Marzo de 2005. [ Links ]














