Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.75 n.156 Medellín set./dez. 2008
LIQUID CRYSTAL RELAXATION IN THREE DIMENSIONS: THE EFFECT OF HYDRODYNAMIC INTERACTIONS
RELAJACIÓN DE CRISTALES LÍQUIDOS EN TRES DIMENSIONES: EL EFECTO DE LAS INTERACCIONES HIDRODINÁMICAS
BRIAN T. GETTELFINGER
Department of Chemical and Biological Engineering, University of Wisconsin-Madison, USA
FRANSISCO R. HUNG
Department of Chemical and Biological Engineering, University of Wisconsin-Madison, USA
JUAN P. HERNANDEZ ORTIZ
Escuela de Ingeniería de Materiales, Universidad Nacional de Colombia, Sede Medellín, jphernandezo@unalmed.edu.co
ORLANDO GUZMAN
Departamento de Física, Universidad Autónoma Metropolitana-Iztapalapa, México
ALEJANDRO D. REY
Department of Chemical Engineering, McGill University, Canada
NICHOLAS L. ABBOTT
Department of Chemical and Biological Engineering, University of Wisconsin-Madison, USA
JUAN J. DE PABLO
Department of Chemical and Biological Engineering, University of Wisconsin-Madison, USA
Recibido para revisar Marzo 30 de 2008, aceptado Julio 8 de 2008, versión final Julio 14 de 2008
ABSTRACT: We investigate the relaxation of two line defects of opposite strength in a confined nematic liquid crystal by solving the coupled tensor order parameter evolution and momentum balance equations in three dimensions. The inclusion of hydrodynamic interactions causes the defects to move at different velocities and slows the overall relaxation process, but this effect is suppressed by increasing the degree of confinement. The most notable flow features that develop in the system are large vortices that surround and follow the defects as they approach each other.
KEYWORDS: liquid crystal, defect relaxation, confinement and hydrodynamic interactions.
RESUMEN: La relajación de dos defectos lineales de magnitud opuesta dentro de un cristal líquido confinado, es investigada solucionando acopladamente la ecuación de evolución del parámetro de orden y las ecuaciones de momentum en tres dimensiones. Las interacciones hidrodinámicas hacen que los defectos se muevan con velocidades diferentes incrementado el tiempo de relajación, sin embargo este efecto desaparece al incrementar el grado de confinamiento. Las características del flujo mas notables en el sistema son grandes vórtices que rodean los defectos a medida que estos se aproximan uno a otro.
PALABRAS CLAVE: cristal líquido, relajación de defectos, confinamiento, interacciones hidrodinámicas.
1. INTRODUCTION
In recent years, nematic liquid crystals have been employed extensively in detection of targeted biological entities, whereby surface events, such as binding of proteins, viruses and microbes [1-4], cause a local change in liquid crystal orientation. These orientational changes are amplified over several thousand molecular lengths through the emergence of mesoscopic defects that are easily detected using optical microscopy [1-4]. Applications to date have relied on optical images of final states, and have therefore been limited to static information. The dynamics or evolution of a sensor could potentially provide a wealth of information about analytes of interest, but to extract this information, one must first develop a realistic model for the dynamics of confined liquid crystals.
Previous theoretical works have given considerable insight into defect structures in the nematic, both around nanoparticles [5-10] and in model biosensors in two dimensions [11, 12]. The dynamics of these calculations have only considered liquid crystal relaxation, where the orientation change with time has been solely due to a free energy gradient. A complete dynamic picture must include hydrodynamic interactions (HI). Several studies have investigated the rheology of the nematic [13-15], but these have employed closure approximations (i.e. 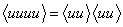 ) and have been limited to two dimensions. A full hydrodynamic description of a nematic, however, necessitates a three-dimensional domain. Denniston et al. [16] have employed the Lattice-Boltzmann method to describe liquid crystal with HI in three dimensions; this method, however, is limited to regimes of finite (but non-zero) Reynolds and Mach numbers, which are unrealistic constraints in sensing applications. In this letter, we solve a detailed molecular model [17] of liquid crystal dynamics on a model sensor, and investigate the differences in defect relaxation that arise when effects of hydrodynamic interactions (HI) are considered.
) and have been limited to two dimensions. A full hydrodynamic description of a nematic, however, necessitates a three-dimensional domain. Denniston et al. [16] have employed the Lattice-Boltzmann method to describe liquid crystal with HI in three dimensions; this method, however, is limited to regimes of finite (but non-zero) Reynolds and Mach numbers, which are unrealistic constraints in sensing applications. In this letter, we solve a detailed molecular model [17] of liquid crystal dynamics on a model sensor, and investigate the differences in defect relaxation that arise when effects of hydrodynamic interactions (HI) are considered.
2. METHODOLOGY
In all calculations, the liquid crystal is characterized by the alignment tensor Q, a symmetric, traceless tensor order parameter [18]. The alignment tensor description is appealing because all the components of Q are continuous, even within a defect core where the components of the director n [18] are discontinuous. The nematic is also frequently characterized using a scalar order parameter S, which captures the degree of local orientational order; because of the abrupt orientation changes associated with defects, a defect core has a low value of S. In this paper, we adopt the convention that the largest eigenvalue of Q is always proportional to the scalar order parameter S, and the corresponding eigenvector is the director n. The Q description thus includes all of the information from the n and S descriptions of the nematic, with the added benefit of continuity at all points in the model domain.
The dynamic equations for Q are based on the model of Stark and Lubensky [17]. Such a model differs slightly from earlier formulations [19-21] in the number of nonlinear terms in Q and the values of some kinetic coefficients. The Stark-Lubensky model agrees exactly with the Ericksen-Leslie equations [22, 23] for the case of uniaxial Q.
The free energy, F, of the liquid crystal is described by a functional of the form [18],
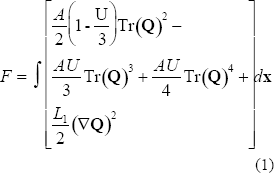
The first three terms of Eq. (1) represent the short-range Landau-de-Gennes contribution to the free energy, which includes an energy scale of the phase transition (A) and a reduced temperature (U). The fourth term of Eq. (1) represents the elastic contribution to the free energy. We assume that all elastic constants are the same, so the elastic constant 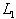 is related to the splay, bend, and twist elastic constant
is related to the splay, bend, and twist elastic constant  by
by 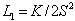 [18].
[18].
The model domain, illustrated in Fig. 1, is a three-dimensional thin film of liquid crystal. This domain is representative of a sensor such as those considered in [1]. The nematic is confined in the z-direction by two walls parallel to the x-y-plane. The periodic lengths in the x- and y-directions, 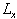 and
and 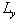 , are three times that in the z-direction:
, are three times that in the z-direction:
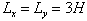 , where H is the separation between the walls. In the following theoretical description, all variables are non-dimensional. Lengths are scaled by the domain thickness, H, and in all figures scaled lengths are denoted with an asterisk (i.e.
, where H is the separation between the walls. In the following theoretical description, all variables are non-dimensional. Lengths are scaled by the domain thickness, H, and in all figures scaled lengths are denoted with an asterisk (i.e. 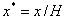 ). Energies have been scaled using the length scale and the elastic constant of the liquid crystal,
). Energies have been scaled using the length scale and the elastic constant of the liquid crystal, 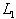 . The resulting simulation time scale,
. The resulting simulation time scale, 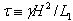 , incorporates the rotational viscosity
, incorporates the rotational viscosity 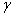 of the nematic. For a typical liquid crystal (5CB) and domain size (
of the nematic. For a typical liquid crystal (5CB) and domain size (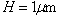 ), the time scale is
), the time scale is 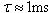 . This choice of scales leaves us with an additional dimensionless number,
. This choice of scales leaves us with an additional dimensionless number, 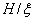 , the ratio of domain thickness to
, the ratio of domain thickness to 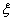 , the coherence length of the liquid crystal; for 5CB,
, the coherence length of the liquid crystal; for 5CB, 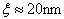 .
.
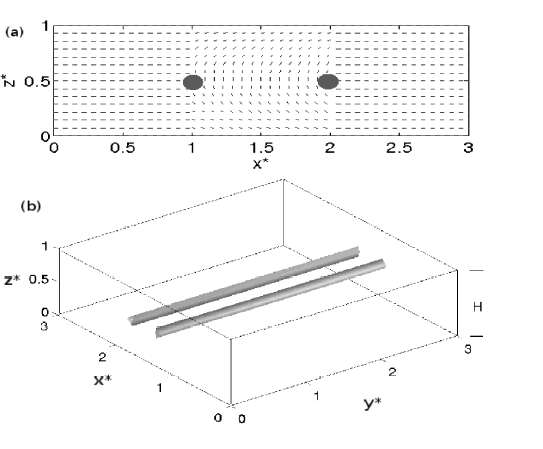
Figure 1. The model domain at 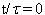 . (a) A cross section of the director field at the
. (a) A cross section of the director field at the 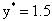 plane The position of the
plane The position of the 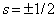 defects are marked with circles. (b) Isosurfaces of
defects are marked with circles. (b) Isosurfaces of 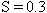 . The line defects form and move toward each other to annihilate
. The line defects form and move toward each other to annihilate
Defect relaxation is examined in the context of the domain in Fig. 1. The initial configuration consists of two domains: between 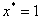 and
and 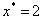 , there is a twisted domain in the liquid crystal, and outside those bounds the nematic is oriented parallel to the x-direction (Fig. 1). This choice of geometry is appealing because theoretical results can be validated experimentally.
, there is a twisted domain in the liquid crystal, and outside those bounds the nematic is oriented parallel to the x-direction (Fig. 1). This choice of geometry is appealing because theoretical results can be validated experimentally.
There is initially no variation in the y-direction, and the system is periodic in both the x- and y-directions. At the 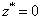 and
and 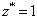 planes, the liquid crystal has strong planar anchoring, with an orientation parallel to the x-direction, and a no-slip condition for velocity (
planes, the liquid crystal has strong planar anchoring, with an orientation parallel to the x-direction, and a no-slip condition for velocity (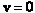 ) is enforced. This choice of initial condition results in two line defects of opposing strength,
) is enforced. This choice of initial condition results in two line defects of opposing strength, 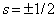 , that form at
, that form at 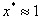 and
and 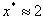 , respectively. These defects move toward the domain center to annihilate one another, thereby minimizing the elastic free energy. Films of thickness
, respectively. These defects move toward the domain center to annihilate one another, thereby minimizing the elastic free energy. Films of thickness 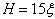 ,
, 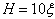 , and
, and 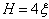 were considered, and the simulation domain is discretized on a
were considered, and the simulation domain is discretized on a 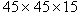 point lattice in three dimensions; this discretization results in a grid spacing that is smaller than the coherence length
point lattice in three dimensions; this discretization results in a grid spacing that is smaller than the coherence length 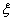 , thereby avoiding an artificial pinning of defects.
, thereby avoiding an artificial pinning of defects.
With this choice of scales, the non-dimensional alignment tensor evolution equation of Stark and Lubensky [17] becomes
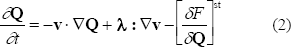
This equation includes three contributions to the change in orientation: convection by flow (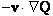 ), alignment with flow (
), alignment with flow (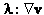 ), and relaxation of free energy (
), and relaxation of free energy (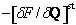 ). The fourth-order tensor
). The fourth-order tensor 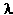 describes the coupling between the momentum and the orientation; for a full description of
describes the coupling between the momentum and the orientation; for a full description of 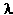 , readers are referred to [17]. The free energy F is given by Eq. (1) [18].
, readers are referred to [17]. The free energy F is given by Eq. (1) [18].
With the introduction of the fluid velocity 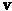 , an accompanying momentum balance must be solved [17]. We assume incompressibility (
, an accompanying momentum balance must be solved [17]. We assume incompressibility (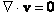 ) and employ the previously described non-dimensionalization. The full momentum balance then becomes
) and employ the previously described non-dimensionalization. The full momentum balance then becomes
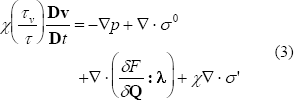
where 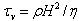 is the viscous time scale,
is the viscous time scale, 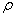 the density and
the density and 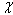 is a ratio of dynamic and rotational viscosities (
is a ratio of dynamic and rotational viscosities (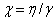 ). For 5CB,
). For 5CB, 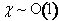 , and for a typical domain size
, and for a typical domain size 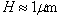 , the viscous time is
, the viscous time is 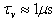 . Recalling that
. Recalling that 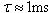 , it can be seen that the left hand side of Eq. (3) is negligible; this omission of the inertial term makes intuitive sense, since in a typical sensor [1], the Reynolds numbers are essentially zero. The momentum balance is thus reduced to a balance of forces,
, it can be seen that the left hand side of Eq. (3) is negligible; this omission of the inertial term makes intuitive sense, since in a typical sensor [1], the Reynolds numbers are essentially zero. The momentum balance is thus reduced to a balance of forces,
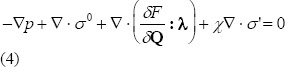
This relation states that pressure forces (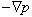 ), elastic forces
), elastic forces 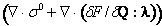 and viscous forces (
and viscous forces (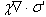 ) must balance each other. Since only the pressure gradient appears in the system, we specify the pressure at the point
) must balance each other. Since only the pressure gradient appears in the system, we specify the pressure at the point 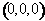 to a value of
to a value of 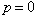 . At each time step, the force balance of Eq. (4) is solved using a finite element method to obtain the velocity field
. At each time step, the force balance of Eq. (4) is solved using a finite element method to obtain the velocity field 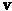 . The resulting velocity field is used in Eq. (2) to update the alignment tensor Q with an implicit Euler scheme.
. The resulting velocity field is used in Eq. (2) to update the alignment tensor Q with an implicit Euler scheme.
3. RESULTS
We first investigate the change of the defects positions with time. Figure 2 shows the distance from the defects cores to the center of the cell (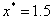 ). The precise location of the defect core is assumed to be the minimum in the scalar order parameter, which is approximated with a quadratic interpolation between grid points. Results in Fig. 2(a-b) correspond to a film of moderate thickness (
). The precise location of the defect core is assumed to be the minimum in the scalar order parameter, which is approximated with a quadratic interpolation between grid points. Results in Fig. 2(a-b) correspond to a film of moderate thickness (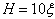 ). When Eq. (4) is ignored (no HI) and relaxation occurs without flow (Fig. 2(a)), the defects move with equal and opposite velocities and are equidistant from the domain center at all times. This picture changes when flows are included and the momentum balance of Eq. (4) is enforced for the same film thickness. Figure 2(b) shows a marked separation in the paths of the two defects. The large elastic stresses associated with the defects necessitate a compensating viscous stress, and the resulting velocity field reinforces the movement of the
). When Eq. (4) is ignored (no HI) and relaxation occurs without flow (Fig. 2(a)), the defects move with equal and opposite velocities and are equidistant from the domain center at all times. This picture changes when flows are included and the momentum balance of Eq. (4) is enforced for the same film thickness. Figure 2(b) shows a marked separation in the paths of the two defects. The large elastic stresses associated with the defects necessitate a compensating viscous stress, and the resulting velocity field reinforces the movement of the 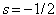 defect while hindering the motion of the
defect while hindering the motion of the 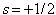 defect. Since the defects no longer move at identical speeds, they do not meet at the exact center of the model domain as they did in the no-flow case. The net effect is that the relaxation of the defects is slowed down by HI. The magnitude of this effect changes, however, depending on the degree of confinement of the liquid crystal. When the nematic is tightly confined (
defect. Since the defects no longer move at identical speeds, they do not meet at the exact center of the model domain as they did in the no-flow case. The net effect is that the relaxation of the defects is slowed down by HI. The magnitude of this effect changes, however, depending on the degree of confinement of the liquid crystal. When the nematic is tightly confined (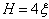 ), as in Fig. 2(c), the presence of flow has a diminished effect on the overall relaxation process, and the paths of the two defects are nearly mirror images. At weaker confinements (
), as in Fig. 2(c), the presence of flow has a diminished effect on the overall relaxation process, and the paths of the two defects are nearly mirror images. At weaker confinements (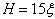 , not shown), the speed anisotropy of the two defects is comparable to that at
, not shown), the speed anisotropy of the two defects is comparable to that at 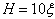 . These results confirm that confinement screens out the effect of HI.
. These results confirm that confinement screens out the effect of HI.
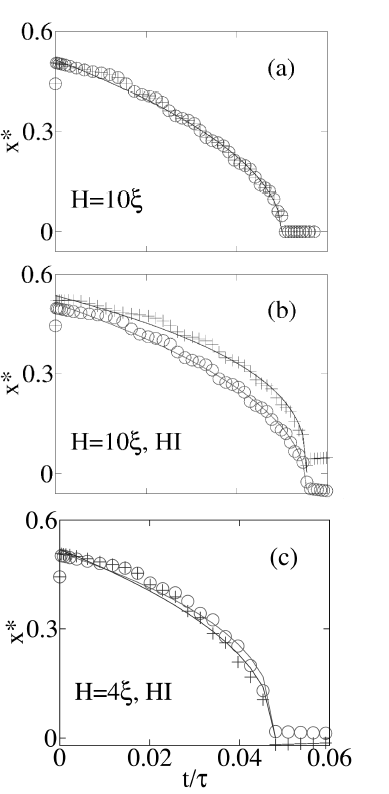
Figure 2. Defect distance from 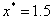 plane vs. time. The
plane vs. time. The 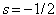 defect is denoted by (o), the
defect is denoted by (o), the 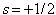 defect by (+). (a) Whit a no-flow condition, the two defects relax along identical paths, meeting in the exact center of the cell. (b) The defects come together more slowly when hydrodynamic interactions are included. Since the two defects now travel with different speeds, they no longer meet at exactly
defect by (+). (a) Whit a no-flow condition, the two defects relax along identical paths, meeting in the exact center of the cell. (b) The defects come together more slowly when hydrodynamic interactions are included. Since the two defects now travel with different speeds, they no longer meet at exactly 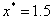 , and the
, and the 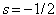 defect crosses the midplane (
defect crosses the midplane (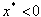 ). (c) In the high confinement (
). (c) In the high confinement (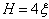 ), the paths of the two defects are nearly identical, even with the inclusion of hydrodynamic interactions
), the paths of the two defects are nearly identical, even with the inclusion of hydrodynamic interactions
In an effort to provide some insight into these flow effects, in Fig. 3 we show streamlines atop scalar order parameter contours for 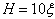 . The large elastic stresses associated with the defects result in a strong initial flow field, illustrated in Fig. 3(a), which reinforces the motion of the
. The large elastic stresses associated with the defects result in a strong initial flow field, illustrated in Fig. 3(a), which reinforces the motion of the 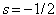 defect and opposes the motion of the
defect and opposes the motion of the 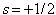 defect. The largest velocity magnitude is greater than
defect. The largest velocity magnitude is greater than 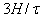 , which is comparable in magnitude to the defects initial approach velocities in the absence of flow. As the defects develop and move, large vortices move along with them, as seen in Fig. 3(b-d). The magnitudes of the strongest flows, however, decay to more moderate values (
, which is comparable in magnitude to the defects initial approach velocities in the absence of flow. As the defects develop and move, large vortices move along with them, as seen in Fig. 3(b-d). The magnitudes of the strongest flows, however, decay to more moderate values (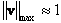 ) at later times. As the defects move into close proximity of one another, each defects approach velocity is more than 20 times the magnitude of the maximum fluid velocity, so the flow contribution to the dynamics at late times is much smaller than at the earliest times. Eventually the defects combine, and the remaining vortices dissipate as the liquid crystal adopts its preferred uniform state. At all times, small but finite flows are present in the y-direction, the effects of which will be the subject of future work. While there is no appreciable variation in the y-direction, the three dimensional nature of the calculations will allow for extension to dynamic systems where a third dimension is required, such as aggregation.
) at later times. As the defects move into close proximity of one another, each defects approach velocity is more than 20 times the magnitude of the maximum fluid velocity, so the flow contribution to the dynamics at late times is much smaller than at the earliest times. Eventually the defects combine, and the remaining vortices dissipate as the liquid crystal adopts its preferred uniform state. At all times, small but finite flows are present in the y-direction, the effects of which will be the subject of future work. While there is no appreciable variation in the y-direction, the three dimensional nature of the calculations will allow for extension to dynamic systems where a third dimension is required, such as aggregation.
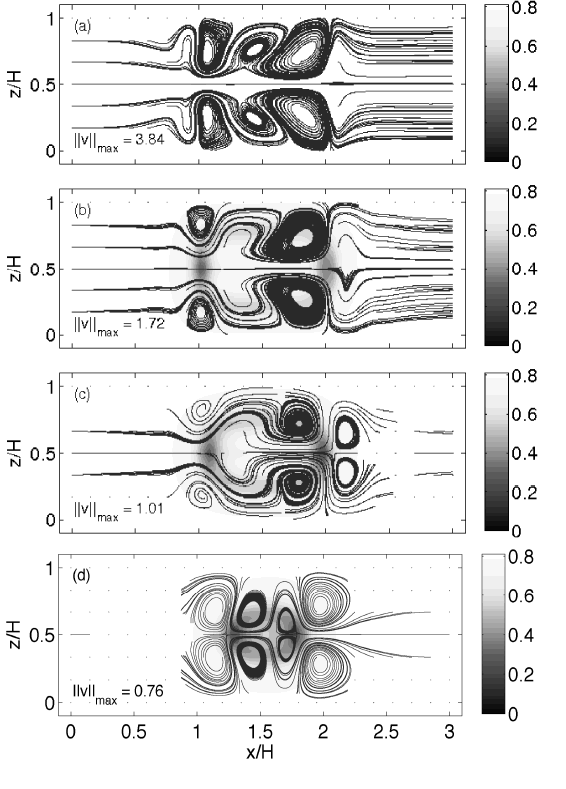
Figure 3. Streamlines atop contours of scalar order parameter for 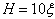 . Velocity magnitudes are in units of
. Velocity magnitudes are in units of 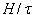 . (a)
. (a) 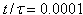 . Flows reinforce the motion of the
. Flows reinforce the motion of the 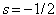 defect (left) but deter the motion of the defect of opposite strength. (b-c)
defect (left) but deter the motion of the defect of opposite strength. (b-c) 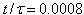 and
and 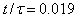 , respectively. The flow strength decays, and distinct vortices begin to develop and shadow the defects. (d) The fully-developed vortices shadow the defects as they relax
, respectively. The flow strength decays, and distinct vortices begin to develop and shadow the defects. (d) The fully-developed vortices shadow the defects as they relax
The initial stress field is responsible for the initial flow field. We consider here only the xx-component of the stresses, since the largest initial flows and the sharpest initial orientation gradients both occur in the x-direction. While the elastic stresses (not pictured) are mirror images about the 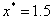 plane, the xx-component of the elastic stress has both positive and negative components. Enforcing the momentum balance of Eq. (4) thus has two effects. First, the viscous stresses at the two defect centers have opposite signs, as seen in Fig. 4(a). Second, since the pressure gradient must have opposite sign, the pressure in Fig. 4(b) shows a peak at the
plane, the xx-component of the elastic stress has both positive and negative components. Enforcing the momentum balance of Eq. (4) thus has two effects. First, the viscous stresses at the two defect centers have opposite signs, as seen in Fig. 4(a). Second, since the pressure gradient must have opposite sign, the pressure in Fig. 4(b) shows a peak at the 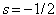 defect and a depression at the
defect and a depression at the 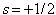 defect. The difference in pressure around these two defects is comparable to that predicted from far-field calculation of pressure around isolated
defect. The difference in pressure around these two defects is comparable to that predicted from far-field calculation of pressure around isolated 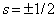 defects. Additionally, the viscous stress has local extrema near the confining walls, which is reasonable given the strong anchoring and no-slip conditions at those surfaces. An analysis of the remaining components of the stress tensor is forthcoming.
defects. Additionally, the viscous stress has local extrema near the confining walls, which is reasonable given the strong anchoring and no-slip conditions at those surfaces. An analysis of the remaining components of the stress tensor is forthcoming.
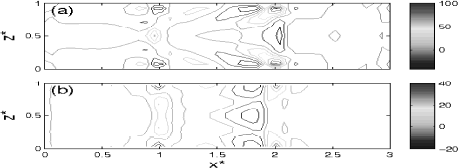
Figure 4. Film of 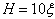 at time
at time 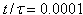 . (a) Contours of the viscous stress component
. (a) Contours of the viscous stress component 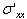 . The extrema in the viscous stress occur at the defect centers and at the confining walls. (b) Pressure field. The pressure compensates for the total stresses in the system
. The extrema in the viscous stress occur at the defect centers and at the confining walls. (b) Pressure field. The pressure compensates for the total stresses in the system
4. CONCLUSIONS
The results presented in this work constitute the first instance in which defect relaxation in a nematic liquid crystal has been considered with a complete, molecular treatment of hydrodynamic interactions. It is found that the dynamics of simple defects change quantitatively when hydrodynamics are properly included. These hydrodynamic interactions will become vitally important when simulating dynamic events in the nematic, such as aggregation processes and dynamic sensing mechanisms. Since controlled experimental studies of defect dynamics in liquid crystals have been extremely limited, our results provide a benchmark that might motivate experiments aimed at understanding liquid crystal dynamics under confinement.
REFERENCES
[1] GUPTA, V.K., SKAIFE, J.J., DUBROVSKY, T.B. and ABBOTT, N.L. Optical Amplification of Ligand-Receptor Binding Using Liquid Crystals. Science 279, 2077, 1998. [ Links ]
[2] SHAH, R. and ABBOTT, N.L. Principles for Measurement of Chemical Exposure Based on Recognition-Driven Anchoring Transitions in Liquid Crystals. Science 293, 1296, 2001. [ Links ]
[3] BRAKE, J.M., DASCHNER, M.K., LUK, Y.Y. and ABBOTT, N.L. Biomolecular Interactions at Phospholipid-Decorated Surfaces of Liquid Crystals. Science 302, 2094, 2003. [ Links ]
[4] SHIYANOVSKII, S.V., SCHNEIDER, T., SMALYUKH, I.I., ISHIKAWA, T., NIEHAUS, G.D., DOANE, K.J., WOOLVERTON, C.J. nd LAVRENTOVICH, O. D. Real-time microbe detection based on director distortions around growing immune complexes in lyotropic chromonic liquid crystals. Phys. Rev. E. 71, 020702, 2005. [ Links ]
[5] GUZMAN, O., KIM, E.B., GROLLAU, S., ABBOTT, N.L. and DE PABLO, J.J. Defect Structure around Two Colloids in a Liquid Crystal. Phys. Rev. Lett. 91, 235507, 2003. [ Links ]
[6] POULIN, P. and WEITZ, D.A. Inverted and multiple nematic emulsions. Phys. Rev. E 57, 626, 1998. [ Links ]
[7] STARK, H. Physics of colloidal dispersions in nematic liquid crystals. Phys. Rep. 351, 387, 2001. [ Links ]
[8] FUKUDA, J. and YOKOYAMA, H. Separation-Independent Attractive Force between Like Particles Mediated by Nematic-Liquid-Crystal Distortions. Phys. Rev. Lett. 94, 148301, 2005. [ Links ]
[9] ARAKI, T. and TANAKA, H. Colloidal Aggregation in a Nematic Liquid Crystal: Topological Arrest of Particles by a Single-Stroke Disclination Line. Phys. Rev. Lett. 97, 127801, 2006. [ Links ]
[10] HUNG, F.R., GUZMÁN, O., GETTELFINGER, B.T., ABBOT, N.L. and DE PABLO, J.J. Anisotropic nanoparticles immersed in a nematic liquid crystal: Defect structures and potentials of mean force. Phys. Rev. E 74, 011711, 2006. [ Links ]
[11] GROLLAU, S., GUZMAN, O., ABBOTT, N.L. and DE PABLO, J.J. Slow dynamics of thin nematic films in the presence of adsorbed nanoparticles. J. Chem. Phys. 122, 024703, 2005. [ Links ]
[12] GUZMAN, O., ABBOTT, N.L. and DE PABLO, J.J. Quenched disorder in a liquid-crystal biosensor: Adsorbed nanoparticles at confining walls. J.Chem. Phys. 122, 184711, 2005. [ Links ]
[13] TOTH, G., DENNISTON, C. and YEOMANS, J.M. Hydrodynamics of Topological Defects in Nematic Liquid Crystals. Phys. Rev. Lett. 88, 105502, 2002. [ Links ]
[14] TSUJI, T. and REY, A.D. Recent Advances in theoretical liquid crystal rheology, Macromolecular Theory and Simulation 7, 623, 1998. [ Links ]
[15] GRECOV, D. and REY, A.D. Steady State and Transient Rheological Behavior of Mesophase Pitch: Part II-Theoretical. Journal of Rheology 49, 175, 2005. [ Links ]
[16] DENNISTON, C., MARENDUZZO, D., ORLANDINI, E. and YEOMANS, J.M. Lattice Boltzmann algorithm for three-dimensional liquid-crystal hydrodynamics. Phil. Trans. R. Soc. Lond. A 362, 1745, 2004. [ Links ]
[17] STARK, H. and LUBENSKY, T. C. Poisson-bracket approach to the dynamics of nematic liquid crystals. Phys. Rev. E 67, 061709, 2003. [ Links ]
[18] DE GENNES, P. and PROST, J. The Physics of Liquid Crystals. Oxford, Oxford University Press, 1995 [ Links ]
[19] OLMSTED, P. D. and GOLDBART, P. Theory of the nonequilibrium phase transition for nematic liquid crystals under shear flow. Phys. Rev. A 41, 4578, 1990. [ Links ]
[20] KUZUU, N. and DOI, M. Constitutive Equation for Nematic Liquid Crystals under Weak Velocity Gradient Derived from a Molecular Kinetic Equation. J. Phys. Soc. Japan 52, 3486, 1983. [ Links ]
[21] BERIS, A. N. and EDWARDS, B. J. Thermodynamics of Flowing Systems. Oxford, Oxford University Press, 1994. [ Links ]
[22] ERICKSEN, J.L. Anisotropic fluids. Arch. Ration. Mech. Anal. 4, 231, 1960. [ Links ]
[23] LESLIE, F.M. Some constitutive equations for anisotropic fluids. Q. J. Mech. Appl. Math. 19, 357, 1966. [ Links ]














