Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353On-line version ISSN 2346-2183
Dyna rev.fac.nac.minas vol.77 no.163 Medellín July/Sept. 2010
UNCOUPLING LAMINAR CONJUGATE HEAT TRANSFER THROUGH CHEBYSHEV POLYNOMIAL
DESACOPLAMIENTO DE LA TRANSFERENCIA DE CALOR CONJUGADA LAMINAR USANDO EL POLINOMIO DE CHEBYSHEV
ANTONIO J. BULA
Departamento de Ing. Mecánica, Universidad del Norte, Barranquilla, Colombia, abula@uninorte.edu.co
RICARDO S. VÁSQUEZ
Universidad del Norte,Barranquilla, rsvasque@mail.usf.edu
Received for review January 23th, 2009, accepted September 9th, 2009, final version October, 6th, 2009
ABSTRACT: The conjugate heat transfer process of cooling a horizontal plate at the leading edge, in steady state condition, was solved considering the fluid flowing in laminar condition and hydro dynamically developed before interacting with a heated plate. The fluid was considered deep enough to allow the growth of a thermal boundary layer with no restrictions. The conservation of mass, momentum and energy equations at the solid and fluid were converted into a non dimensional form. The heated body presents a constant heat flux at the bottom side, and convective heat transfer at the top side. The interface temperature was obtained using the Chebyshev polynomial approximation. In order to verify the results obtained using the Chebyshev polynomial approximation, the results obtained from the analytical solution for the solid, were compared with the results attained with commercial CFD software, FIDAP®. The solution considered the calculation of the local and average heat transfer coefficient, the local and average Nusselt number, the local and average Biot number, and different temperature distributions at the interface.
KEYWORDS: Chebyshev's polynomial, conjugate heat transfer.
RESUMEN: El proceso de transferencia de calor conjugada para enfriamiento de una placa en estado estable ha sido resuelto considerando el fluido laminar e hidrodinámicamente desarrollado antes de entrar en contacto con la placa. El fluido es lo suficientemente profundo y permite el crecimiento de la capa límite térmica sin restricciones. Las ecuaciones de continuidad, cantidad de movimiento y energía, en el sólido y en fluido fueron adimensionalizadas. La temperatura en la interface se obtiene por medio del polinomio de Chebishev, y los resultados obtenidos fueron verificados con la solución obtenida por medio de software CFD comercial, FIDAP ®. La solución ncluyo el cálculo del coeficiente de transferencia de calor, el número de Nusselt, el número de Biot, todos tanto local como promedio. La distribución de temperatura en la interface también fue obtenida.
PALABRAS CLAVES: Polinomio de Chebyshev, transferencia de calor conjugada.
1. INTRODUCTION
The conjugate heat transfer problem is present when heat is exchanged between a solid and a fluid. The common approximation considers a boundary condition between the solid and the fluid that uncouples the phenomena, to solve the conduction heat transfer situation for the solid,
and the convection heat transfer situation for the fluid. This can be accomplished by a linear combination of orthogonal Chebyshev polynomials that guarantees the solution of the partial differential equation at the solid, and helps to find the non dimensional parameters that control the convection heat transfer problem. Analytical and numerical solutions for cooling electronic components have allowed proposing some geometrical configurations that enhance the heat transfer process, in order to obtain the temperature distribution inside electronics boards [1, 2, 3]. The analytical part helped to optimize the selection of materials, configuration and location to the components in order to reduce the maximum temperature in the substrate, and allowed estimation of heat released by the source and its effect on the temperature distribution. In 1998 [4] presented experimental results correlated through empirical expressions for flat plates with constant heat sources. The conjugate heat transfer process has been studied numerically [5, 6] presenting numerical solutions for jets impinging over flat surfaces under laminar flow. Numerical results were compared to experimental data gathered by [7]. A work by [8] used a Chebyshev approximation in order to solve a two dimensional, incompressible, viscous flow of a biomagnetic fluid over a heated plate. The numerical solution obtained for the coupled non linear boundary value problem achieved high accuracy, and it was compared to a finite difference method solution showing the efficiency of the Chebyshev approximation. Complex problems [9], such as the modeling of magneto hydrodynamic flow of micro polar, viscous, incompressible and electric conducting fluid from an isothermal stretching with suction and blowing in a porous media has also used the Chebyshev approximation. [10] developed a hybrid finite difference code for the simulation of unsteady incompressible pipe flow, using the Chebyshev approximation for the radial coordinate. The effectiveness of the Chebyshev approximation was studied by [11], he presented a new approximation in order to achieve better results when using this technique, especially in the modeling of hydrodynamic problems that include Bénard convection problem, and Orr-Sommerfeld for parallel flow. The heat transfer process between a flat plate and a fluid is a thermal model with many applications, and in order to have a solution for the leading edge area, the Chebyshev approximation will be used to introduce an interface boundary condition depending on the fluid and flow characteristics.
2. MATHEMATICAL MODEL
The orthogonal Chebyshev polynomials result from the solution of the following equation
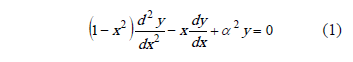
The nth grade polynomial is represented by:
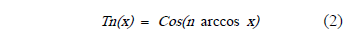
And the trigonometric expressions from (3) are used for solving the polynomial,
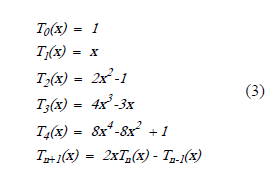
The Chebyshev polynomials are orthogonals in the interval [-1, 1], and the weight function is 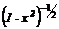 . For this case,
. For this case,
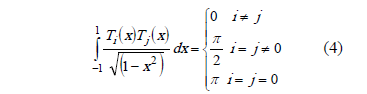
The polynomial 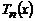 has n ceros, a maximum and a minimum, located according to the following equations,
has n ceros, a maximum and a minimum, located according to the following equations,
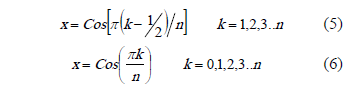
Because of this property, the Chebyshev polynomials are used for polynomial approximations, and they also satisfy a discrete orthogonal condition, if 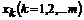 are the m ceros for
are the m ceros for 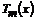 . Then,
. Then,
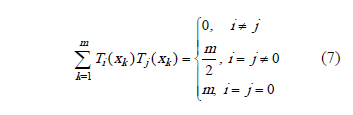
The combination of (1 - 7) helps to obtain an approximation function under the following conditions, 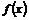 is an arbitrary function in an interval [-1,1], there are N coefficients
is an arbitrary function in an interval [-1,1], there are N coefficients 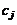 ,
, 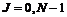 , defined by:
, defined by:
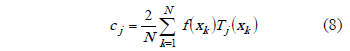
Replacing (6) into (8),
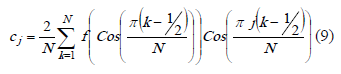
With this, the approximation becomes:
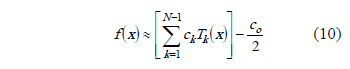
For any limits, [a, b], and changing variables,
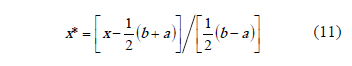
2.1 Governing equations and boundary conditions
Assuming an incompressible fluid, with constant properties, moving according to Fig. 1, the equations that describe the conjugate heat transfer are:
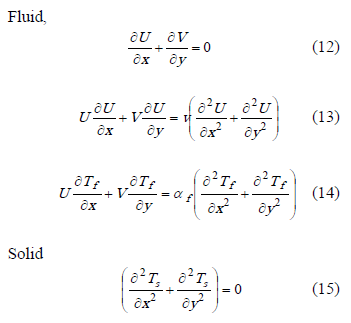
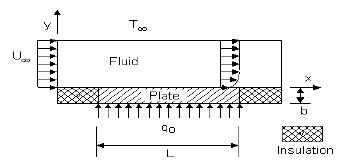
Figure 1. Schematic of a rectangular plate under the influence of a laminar flow
Equations (12 - 15) are subjected to the following boundary conditions,
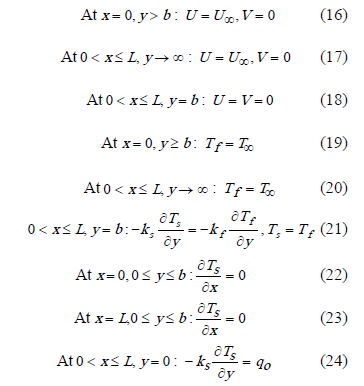
Equations (12 - 15) and the boundary conditions (16 - 24) were converted in a dimensionless form, using the following non dimensional terms,
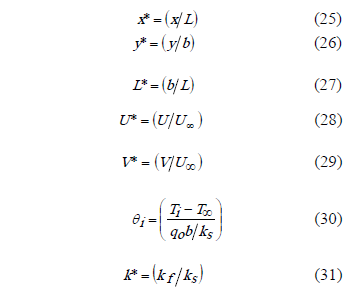
Using the dimensionless variables presented in (25 - 31), the equations turned into the following dimensionless form:
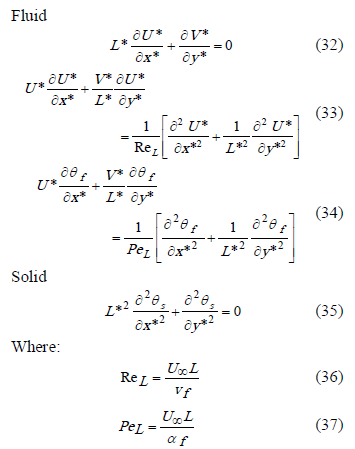
The boundary conditions for (32 - 35) are,
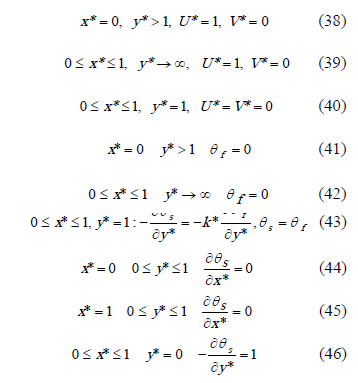
In order to obtain an analytic solution to the heat conduction problem in the solid, the temperature at the interface must be known. This temperature can be represented as a linear combination of Chebyshev polynomials according to (47)
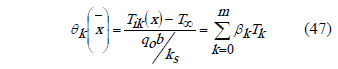
Where:
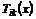 : Temperature at the solid - fluid interface.
: Temperature at the solid - fluid interface.
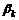 : Coefficients of the linear combination.
: Coefficients of the linear combination.
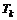 : order k, Chebyshev polynomial.
: order k, Chebyshev polynomial.
This equation represents the solution for the problem presented in Fig. (2)
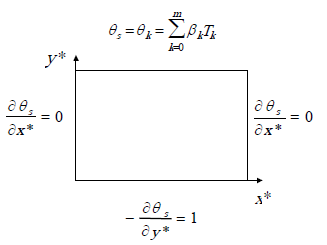
Figure 2. Two dimensional heat conduction problem at the plate
Due to non homogeneous boundary conditions at the y*coordinate, a substitution is used to take care of one the non homogeneity. The substitution is as follows:
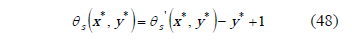
The boundary conditions for the substitution variables are:
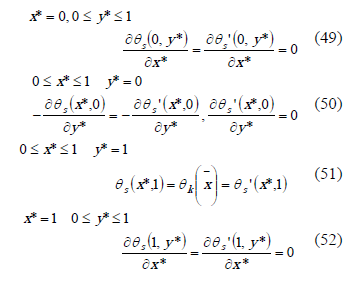
The Sturm-Liouville problem is present in the 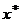 axis, due to the homogeneous conditions. The solution is as follows:
axis, due to the homogeneous conditions. The solution is as follows:
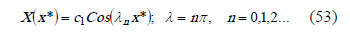
The solution for the differential equation 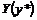 is the following,
is the following,
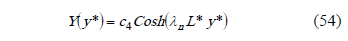
The general solution is,
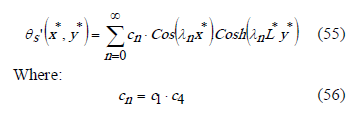
To obtain 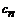 , the boundary condition at the solid fluid interface is evaluated.
, the boundary condition at the solid fluid interface is evaluated.
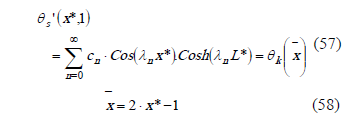
This is due to the orthogonal properties of the Chebyshev polynomials at the [-1, 1] interval. Using this condition:
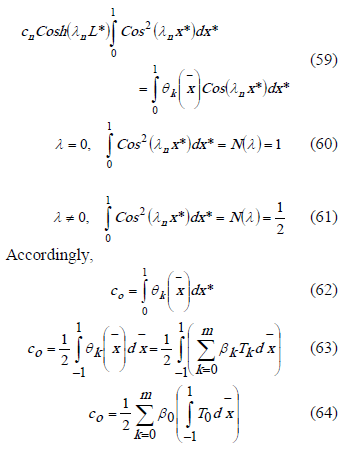
From the orthogonal condition of the Chebyshev polynomials,
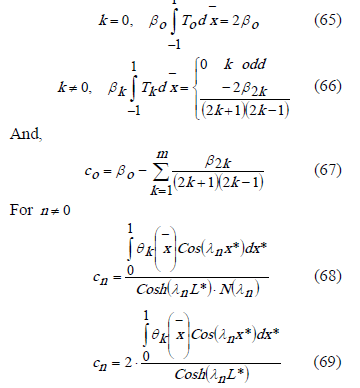
The solution of (48) is as follows
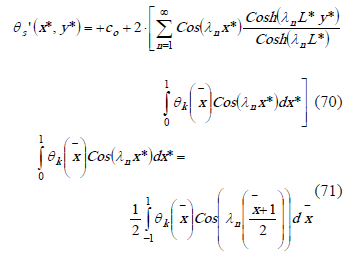
The non dimensional temperature solution for the solid,
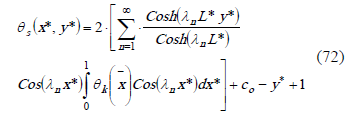
2.3 Local convective heat transfer coefficient and local Nusselt number
From an energy balance at the interface,
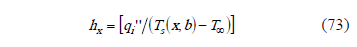
From the boundary conditions:
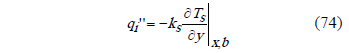
Introducing the non dimensional variables,
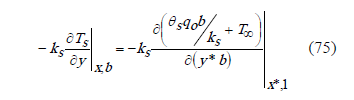
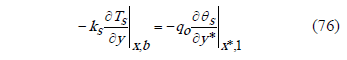
From the Chebyshev polynomial solution:
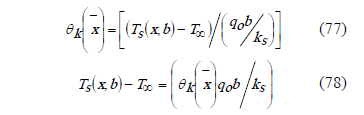
Replacing in (76),
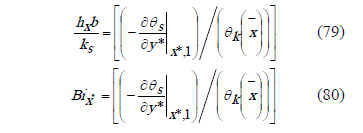
Derivation of 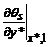 , and evaluating at
, and evaluating at 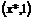 , and replacing in (80),
, and replacing in (80),
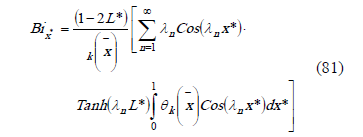
The local Nusselt number can be obtained from:
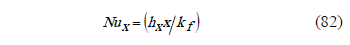
Manipulating the equation,
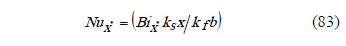
Using the non dimensional variables,
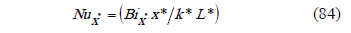
Replacing (85) in (88),
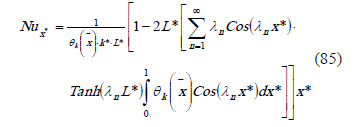
2.4 Average convective heat transfer coefficient and average Nusselt number
The average convective heat transfer coefficient can be obtained according to Bula 1999, [7],
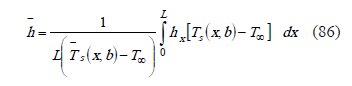
Evaluating each term of (85), from (47) and (77),
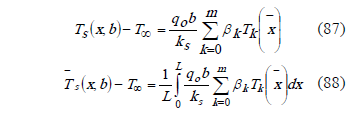
Derivation of (25),
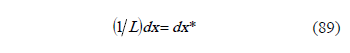
Replacing (88) in (72),
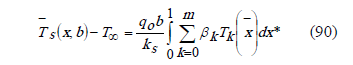
Derivation of (58),
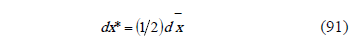
Replacing (91) in (90),
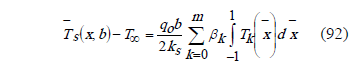
From (65),
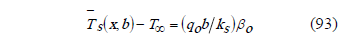
From the local Biot number definition,
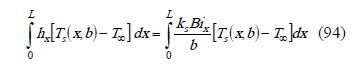
From (86),
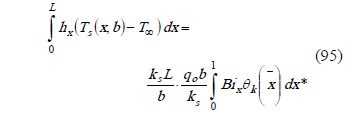
Replacing Biot number from (81) into (95),
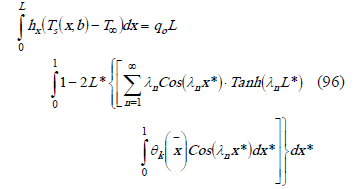
From the Chebyshev polynomials properties,
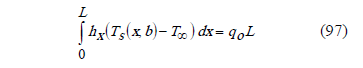
Replacing (88) and (97) in (86),
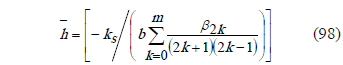
The average Biot number can be calculated according to the following equation,
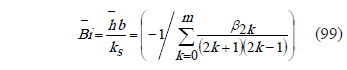
The average Nusselt number can be calculated according to the following equation,
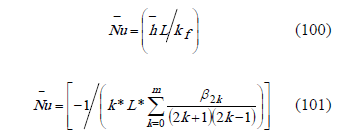
Different temperature distributions can be considered, and for each one of them, Biot and Nusselt number, as well as expressions for the average values of the heat transfer coefficient, can be developed. In this case, only cubic temperature profile will be considered.
2.5 Cubic temperature profile
The temperature at the interface is represented by the following expression,
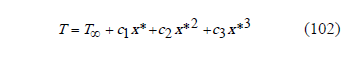
In a non dimensional form,
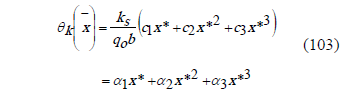
The Chebyshev polynomials parameters and the equation are: for this case are,
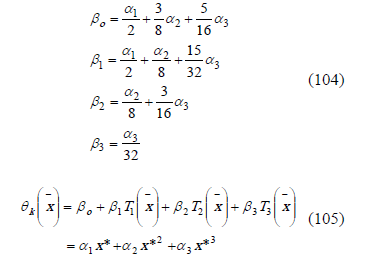
The temperature in the plate,
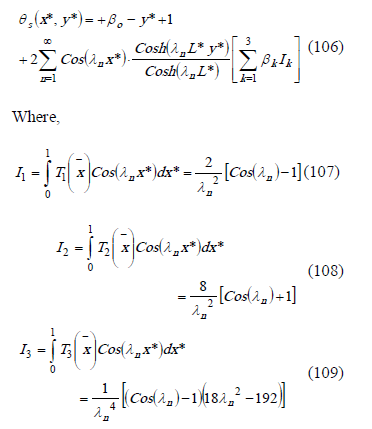
The local Biot number, Biot number, average heat transfer coefficient, local Nusselt number, and average Nusselt number, are presented in the following equations,
3. RESULTS AND DISCUSSION
A computational program was developed to solve the general heat conduction equation in the solid, taking into consideration the boundary condition at the interface represented by the a Chebyshev polynomial. In order to validate the model, the non dimensional conjugate heat transfer problem was solved using commercial CFD software, FIDAP®. The domain design considered the growth of the hydrodynamic and thermal boundary layer, and the height was calculated considering the maximum Reynolds number, Prandtl number, and the thickness to plate length ratio to be used. In order to determine the number of elements for accurate numerical solution, computation was performed for several combinations of grid distribution in the radial and vertical directions covering the solid and fluid regions. It was noticed that the solution became grid independent when the number of divisions in the horizontal direction was increased to 20 and at least 36 in the vertical direction. The comparison considered three different Reynolds numbers, with different order of magnitude, 5x105, 5x104, and 1x103, representing constant temperature, linear temperature, and cubic temperature profiles respectively. Figures 3 and 4, present the non dimensional isothermal lines inside the solid, using FIDAP and the solution of the semi analytical model, for a Reynolds number of 5x105. It can be observed that there is an excellent agreement between the two solutions presented, and the assumption of a constant temperature at the interface is valid due to the one dimensional temperature distribution.
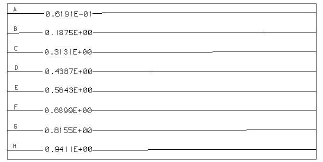
Figure 3. Solid temperature distribution. Numerical simulation in FIDAP (Oil MIL 7808 - Constantan, Re = 5x105, L*=0.5)

Figure 4. Solid temperature distribution. Solution of the semi analytical model (Oil MIL 7808 - Constantan, Re = 5x105, L*=0.5)
Figure 5 presents the temperature at the interface, calculated using FIDAP and the semi analytical model, as well as the error between the solutions. It can be seen that the error ranges between cero and 0.5%, presenting the maximum deviation in the right hand side, where the fluid gets in contact with the solid. The temperature at the interface is quite constant, ranging from cero to 6x10-3.
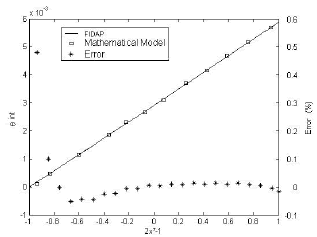
Figure 5. Temperature at the interface and error from the mathematical model and FIDAP solution (Oil MIL 7808 - Constantan, Re = 5x105, L*=0.5)
Figures 6 and 7 present the temperature distribution inside the solid for the numerical solution and the semi analytical model for a Reynolds number in the fluid of 5x104. It is noticed a good agreement between the two solutions. In this case, there is almost a one dimensional distribution with a tendency of the isothermal lines to concentrate around the point where the fluid gets in contact with the solid.

Figure 6. Solid temperature distribution. Numerical simulation in FIDAP (Oil MIL 7808 - Constantan, Re = 5x104, L*=0.5)

Figure 7. Solid temperature distribution. Solution of the semi analytical model (Oil MIL 7808 - Constantan, Re = 5x104, L*=0.5)
Figure 8 presents the temperature at the interface, calculated using FIDAP and the semi analytical model, as well as the error between the solutions. It can be seen that the error goes up to 3%, presenting the maximum deviation in the right hand side, where the fluid gets in contact with the solid. The non dimensional temperature at the interface presents an almost linear behavior, going from zero to 0.07.
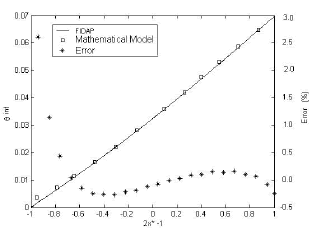
Figure 8. Temperature at the interface and error from the mathematical model and FIDAP solution (Oil MIL 7808 - Constantan, Re = 5x104, L*=0.5)
Figures 9 and 10 present the temperature distribution inside the solid for the numerical solution and the semi analytical model for a Reynolds number in the fluid of 1x103. It is observed there is a good agreement between the two solutions. In this case, it is noticed that the effect of the slow motion of the fluid turns the temperature distribution in the solid completely two dimensional, and the isothermal lines become concentric around the point where the fluid gets in contact with the solid.
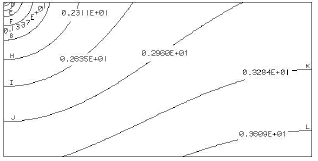
Figure 9. Solid temperature distribution. Numerical simulation in FIDAP (Oil MIL 7808 - Constantan, Re = 1x103, L*=0.5)

Figure 10. Solid temperature distribution. Solution of the semi analytical model (Oil MIL 7808 - Constantan, Re = 1x103, L*=0.5)
Figure 11 presents the temperature at the interface, calculated using FIDAP and the semi analytical model, as well as the error between the solutions. It can be seen that the error goes up to 0.3%, presenting the maximum deviation in the right hand side, where the fluid gets in contact with the solid. The behavior of the non dimensional temperature at the interface could be approximated by a second order polynomial, and it ranges from zero to 3.
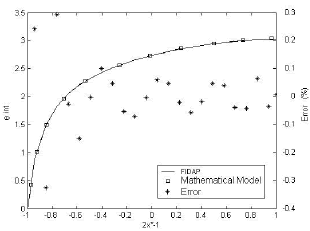
Figure 11. Temperature at the interface and error from the mathematical model and FIDAP solution. (Oil MIL 7808 - Constantan, Re = 1x103, L*=0.5)
Figure 12 shows the variation of average Nusselt number with Reynolds number. In this figure is compared the classic average Nusselt number and the average Nusselt number obtained from simulation in FIDAP and the semi analytical model. The variation of average Nusselt number is similar to FIDAP and the semi analytical mathematical model, but in both cases, the classic average Nusselt number is lower than the one obtained by numerical methods. This shows that the classic average Nusselt number is conservative
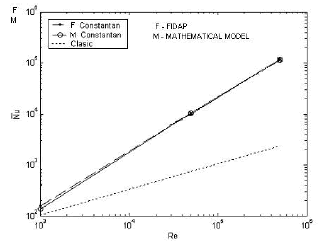
Figure 12. Comparison between the classic average Nusselt number and average Nusselt number obtained from FIDAP solution and the semi analytical model (Oil MIL 7808 - Constantan, Re = 1x103, L*=0.5)
4. CONCLUSIONS
According to these results, it can be concluded that the Chebyshev polynomial approximation can be used to uncouple the conjugate heat transfer problem, accommodating the temperature distribution at the interface depending on the Reynolds number. Also, the constant temperature and linear temperature approximation for the interface temperature could be discarded, considering a third order polynomial, which accommodate for the different temperature distributions.
NOMENCLATURE
B Plate thickness
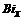 Local Biot number,
Local Biot number, 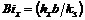
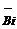 Average Biot number,
Average Biot number, 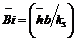
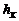 Local convective heat transfer coefficient.
Local convective heat transfer coefficient.
 Convective heat transfer coefficient
Convective heat transfer coefficient
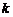 Thermal conductivity,
Thermal conductivity,
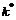 Thermal conductivity ratio,
Thermal conductivity ratio, 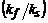
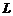 Length of the plate
Length of the plate
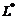 Dimensionless length,
Dimensionless length, 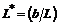
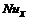 Local Nusselt number,
Local Nusselt number, 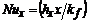
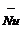 Average Nusselt number,
Average Nusselt number, 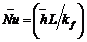
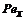 Local Peclet number x,
Local Peclet number x, 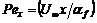
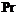 Prandtl number
Prandtl number
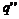 Heat flow per unit area
Heat flow per unit area
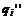 Heat flow at the solid-fluid interface
Heat flow at the solid-fluid interface
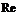 Reynolds number in L,
Reynolds number in L, 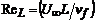
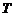 Temperature
Temperature
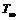 Fluid free stream temperature
Fluid free stream temperature
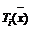 Chebyshev polynomial, i order.
Chebyshev polynomial, i order.
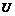 Horizontal Velocity
Horizontal Velocity
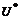 Dimensionless Horizontal Velocity
Dimensionless Horizontal Velocity
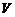 Vertical Velocity
Vertical Velocity
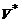 Dimensionless Vertical Velocity
Dimensionless Vertical Velocity
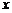 Position in the horizontal axis
Position in the horizontal axis
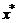 Dimensionless position, horizontal axis
Dimensionless position, horizontal axis
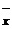 Chebyshev variable
Chebyshev variable
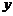 Position in the vertical axis
Position in the vertical axis
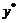 Dimensionless position, vertical axis
Dimensionless position, vertical axis
Greek symbols
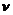 Kinematic viscosity
Kinematic viscosity
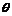 Dimensionless temperature
Dimensionless temperature
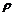 Density
Density
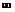 Infinite
Infinite
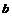 Plate thickness
Plate thickness
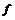 Fluid
Fluid
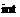 Interface
Interface
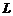 Length of the plate
Length of the plate
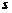 Solid
Solid
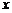 Along the x axis
Along the x axis
REFERENCES
[1] Negus, K., Yovanovich, M. Thermal Analysis and Optimization of Convectively-Cooled Microelectronic Circuit Boards. Proceedings of the AIAA/ASME 4th Thermophysics and Heat Transfer Conference, Boston , USA , 57, 67-175, 1986. [ Links ]
[2] Culham, J., Lee S., Yovanovich M. Non-Iterative Technique for Computing Temperature Distributions in Flat Plates with Distributed Heat Sources and Convective Cooling. Proceedings of the ASME/JSME Thermal Engineering Joint Conference, Honolulu , USA , 3, 403-409, March, 1987. [ Links ]
[3] Culham J., Lee S., Yovanovich M. The effect of Common Design Parameters on the Thermal Performance of Microelectronic Equipment; Part II - Forced Convection. Proceedings of the ASME National Heat Transfer Conference, Minneapolis , USA , 171, 55-60, July 1991. [ Links ]
[4] Hwang, J. Conjugate heat transfer for developing flow over multiple discrete thermal sources flush-Mounted on the wall. Journal of Heat Transfer.120, 510-514, 1998. [ Links ]
[5] Rahman, M., Bula, A. Conjugate Heat Transfer during Free Jet Impingement of A High Prandtl Number Fluid. Numerical Heat Transfer Journal, Part B. 36, 139-162, 1999. [ Links ]
[6] Bula, A., Rahman, M. Solids Thermal Response to Jet Impingement. Proceedings of the International Conference of the Association of Science and Technology for Development, Marbella , Spain , 370-375, September 2001. [ Links ]
[7] Leland, J., Pais, M. Free Jet Impingement heat Transfer of a High Prandtl number Fluid under Conditions of Highly Varying Properties. Journal of Heat Transfer. 121, 592-597, 1999. [ Links ]
[8] Tzirtzilakis, E., Tanoudis, G. Numerical Study of Biomagnetic Fluid over a Stretching Sheet with Heat Transfer. International Journal of Numerical Methods for Heat and Fluid Flow. 13-7, 830-848, 2003. [ Links ]
[9] Elshehawey, E., Eldabe, N., Elbarbary, E. and Elgazery, N. Chebyshev Finite Difference Method for the Effect of Hall and Ion-Slip Currents on Magneto Hydrodynamic Flow with Variable Thermal Conductivity, Canadian Journal of Physics. 82-9, 701-715, 2004. [ Links ]
[10] Reuter J, Rempfer D. "Analysis of Pipe Flow Transition. Part I. Direct Numerical Simulation". Theoretical and Computational Fluid Dynamics. 7, 273-292, 2004. [ Links ]
[11] Bourne, D. Hydrodynamic stability, the Chebyshev Tau Method and Spurious Eigen Values, Continuum Mechanics and Thermodynamics, 15, 571- 579, 2003. [ Links ]














