Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.77 n.163 Medellín jul./set. 2010
PRODUCTION SCHEDULING WITH SEQUENCE-DEPENDENT SETUPS AND JOB RELEASE TIMES
PROGRAMACIÓN DE LA PRODUCCIÓN CON TIEMPOS DE PREPARACIÓN DEPENDIENTES DE LA SECUENCIA Y FECHAS DE LLEGADA DE TRABAJOS
JAIRO R. MONTOYA-TORRES
Universidad de La Sabana, Chía, Colombia, jairo.montoya@unisabana.edu.co
MILTON SOTO-FERRARI
Universidad del Norte, Barranquilla, Colombia
FERNANDO GONZÁLEZ-SOLANO
Universidad del Norte, Barranquilla, Colombia
Received for review July 3th, 2009, accepted March 4th, 2010, final version April, 4th, 2010
ABSTRACT: This paper studies a short-term production scheduling problem inspired from real-life manufacturing systems consisting on the scheduling a set of jobs (production orders) on both a single machine and identical parallel machines with the objective of minimizing the makespan or maximum completion time of all jobs. Jobs are subject to release dates and there are sequence-dependent machine setup times. Since this problem is known to be strongly NP-hard even for the single machine case, this paper proposes a heuristic algorithm to solve it. The algorithm uses a strategy of random generation of various execution sequences, and then selects the best of such schedules. Experiments are performed using random-generated data and show that the heuristic performs very well compared against the optimal solution and lower bounds, and requiring short computational time.
KEYWORDS: Scheduling, sequence-dependent setup times, release dates, randomness, heuristic.
RESUMEN: Este artículo estudia un problema de programación de la producción en el corto plazo inspirado de sistemas de fabricación reales en los cuales se tiene un conjunto de tareas (órdenes de producción) tanto en una configuración de una máquina como en máquinas paralelas idénticas con el objetivo de minimizar el lapso de fabricación o tiempo máximo de terminación de todos los trabajos. Las tareas están sujetas a fechas de disponibilidad diferentes y existen tiempos de preparación de las máquinas dependientes de la secuencia de procesamiento. Puesto que este problema es conocido como fuertemente NP-completo, incluso para el caso de una máquina simple, este artículo propone un algoritmo heurístico para resolverlo. El algoritmo emplea una estrategia de generación aleatoria de varias secuencias de procesamiento de los trabajos y luego selecciona el mejor de estos programas. Se desarrollaron experimentos computacionales empleando datos generados aleatoriamente. Los resultados muestran que el procedimiento propuesto se desempeña muy bien comparado con la solución óptima o con cotas inferiores, requiriendo un menor tiempo de cálculo.
PALABRAS CLAVE: Programación de la producción, tiempos de preparación dependientes de la secuencia, fechas de disponibilidad, aleatoriedad, heurística.
1. INTRODUCTION
Scheduling is a decision-making process that is used on a regular basis in many manufacturing and services industries. It deals with the allocation of resources (often simply called machines) to tasks (jobs) over given time periods and its goal is to optimize one or more objectives [1].
Efficient production schedules can result in substantial improvements in productivity and cost reductions. Generating a feasible schedule that best meets management's objectives is a difficult task that manufacturing firms face every day [2].
In many industries, the decision to manufacture multiple products on common resources results in the need for changeover and setup activities, representing costly disruptions to production processes. Therefore, setup reduction is an important feature of the continuous improvement program of any manufacturing, and even service, organization. It is even more critical if an organization expects to respond to changes like shortened lead times, smaller lot sizes, and higher quality standards. Every scheduler should understand the principles of setup reduction and be able to recognize the potential improvements.
Setup time, in general, can be defined as the time required to prepare the necessary resource (e.g., machines, people) to perform a task (e.g., job, operation). Setup times can be of two types: sequence-independent and sequence-dependent. If setup time depends solely on the task to be processed, regardless of its preceding task, it is called sequence-independent. On the other hand, in the sequence-dependent type, setup time depends on both the task and its preceding task [3].
Scheduling problems with sequence-dependent setup times can be found in various production, service, and information processing environments [3]. For example, in a computer system application, a job requires a setup time to load a different compiler if the current compiler is not suitable. In a printing industry, a setup time is required to prepare the machine (e.g., cleaning) which depends on the color of the current and immediately following jobs. In a textile industry, setup time for weaving and dying operations depends on the jobs sequence. In a container/bottle industry, setup time relies on the sizes and shapes of the container/bottle, while in a plastic industry different types and colors of products require setup times. Similar situations arise in chemical, pharmaceutical, food processing, metal processing, paper industries, and many other industries/areas.
As stated by Allahverdi and Soroush [3], in today's manufacturing scheduling problems it is of significance to efficiently utilize various resources. Treating setup times separately from processing times allows operations to be performed simultaneously and hence improves resource utilization. This is particularly important in modern production management systems such as Just-in-Time (JIT), Optimized Production Technology (OPT), Group Technology (GT), cellular manufacturing, and time-based competition. The benefits of reducing setup times include [3]: reduced expenses, increased production speed, increased output, reduced lead times, faster changeovers, increased competitiveness, increased profitability and satisfaction, enabling lean manufacturing, smoother flows, broader range of lot sizes, lower total cost curve, fewer stock-outs, lower inventory, lower minimum order sizes, higher margins on orders above minimum, faster deliveries, and increased customer satisfaction. The importance and benefits of incorporating setup times in scheduling research has been investigated by many researchers (see for instance [4,5,6,7,8].
This paper studies the problem of job scheduling on both a single machine and identical parallel machines with sequence-dependent setup times and release dates. The single-machine environment does represent a building block for more complex configurations. Many researchers have dealt with job scheduling problems on a single-machine under different constraints. A fundamental issue is the inherent difficulty of one machine scheduling problems that involve sequence-dependent setup times. Pinedo [1] showed that the makespan minimization on a single machine with sequence-dependent setup times is strongly NP-hard, which means that is not possible to find optimal solutions in reasonable computational time for large-sized instances. For the parallel machine case, computational results are not encouraging. In this paper, we are interested in studying such scheduling problems adding the constraint of jobs having unequal release times.
This paper is organized as follows. Section 2 is devoted to analyze the problem under a single resource (single-machine) environment. Section 3 extends the study for the multiple parallel machines context. Related relevant literature and computational experiments are presented respectively within both sections. The paper ends in section 4 by presenting the conclusions.
2. ANALYSIS OF THE SINGLE-MACHINE CASE
Formally, we first consider the problem of scheduling a set of n jobs on one machine. Job j, with j=1,...,n, is characterized by its integer processing time 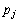 and an non-negative integer release date
and an non-negative integer release date 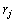 . Sequence-dependent machine setup times are also considered. That is, if job k is executed on the machine immediately after job j, a setup time
. Sequence-dependent machine setup times are also considered. That is, if job k is executed on the machine immediately after job j, a setup time 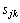 is needed during which the machine cannot process any job. We consider the objective of minimizing the makespan of the schedule or total completion time of all jobs. Using the classical notation in Scheduling Theory, this problem is noted as
is needed during which the machine cannot process any job. We consider the objective of minimizing the makespan of the schedule or total completion time of all jobs. Using the classical notation in Scheduling Theory, this problem is noted as 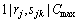 . When all jobs have equal release dates (
. When all jobs have equal release dates (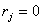 ,
, 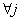 ), the one machine scheduling problem, noted as
), the one machine scheduling problem, noted as 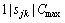 , is equivalent to the Traveling Salesman Problem (TSP), which is known to be NP-hard [1]. This means that no efficient (polynomial-time) algorithm can be found to solve large-sized instances. Hence, the problem considered in this paper is at least that difficult.
, is equivalent to the Traveling Salesman Problem (TSP), which is known to be NP-hard [1]. This means that no efficient (polynomial-time) algorithm can be found to solve large-sized instances. Hence, the problem considered in this paper is at least that difficult.
The problem of job scheduling with sequence-dependent machine setup times have been largely studied in the literature. State of the art surveys are presented in [9,10,11]. For the one machine case, even though complexity analysis is not encouraging, researchers have developed exact approaches based on branch and bound, dynamic programming or integer linear programming. The objective function under study in this paper is the makespan and can be expressed as:
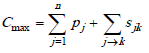
When setup times are dependent on the sequence, minimizing makespan becomes equivalent to minimizing the total setup time. That is because the sum of processing times remains a constant through the whole scheduling when all information about jobs is deterministic and known at the initial time of scheduling. This problem corresponds to what is usually called the Traveling Salesman Problem (TSP). In a TSP, each city corresponds to a job and the distance between cities corresponds to the time required to change from one job to another. If the setup times for all pairs of jobs are indifferent to their sequencing order when scheduled consecutively, the scheduling problem is equivalent to a symmetrical TSP, otherwise, it is equivalent to an asymmetrical TSP [9].
One of the pioneering works on the sequence-dependent setup time problem was presented by Gilmore and Gomory [12] who modeled and solved the problem as a TSP. Presby and Wolfson [13] provided an optimization algorithm that is suitable only for small problems. Bianco et al. [14] formulated the problem 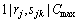 as a mixed integer linear program and developed a heuristic algorithm using lower bounds and dominance criteria. For the problem
as a mixed integer linear program and developed a heuristic algorithm using lower bounds and dominance criteria. For the problem 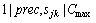 , He and Kusiak [15] proposed a simpler mixed-integer formulation and a fast heuristic algorithm of low computational time complexity. Ozgur and Brown [2] developed a two-stage traveling salesman heuristic procedure for the problem where similar products produced on the machine can be partitioned into families.
, He and Kusiak [15] proposed a simpler mixed-integer formulation and a fast heuristic algorithm of low computational time complexity. Ozgur and Brown [2] developed a two-stage traveling salesman heuristic procedure for the problem where similar products produced on the machine can be partitioned into families.
There are several works presented in the literature that consider other objective functions. Barnes and Vanston [16] combined branch and bound with dynamic programming to solve the problem noted as 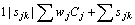 . For the case of precedence constraints with a special structure (chains), Uzsoy et al. [8] developed branch and bound algorithm for
. For the case of precedence constraints with a special structure (chains), Uzsoy et al. [8] developed branch and bound algorithm for  and Uzsoy et al. [17] developed dynamic programming algorithms for
and Uzsoy et al. [17] developed dynamic programming algorithms for  and
and 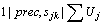 , where the objective function corresponds to the minimization of the number of tardy jobs. Tan and Narasimhan [18] proposed a simulated annealing algorithm to minimize total tardiness (
, where the objective function corresponds to the minimization of the number of tardy jobs. Tan and Narasimhan [18] proposed a simulated annealing algorithm to minimize total tardiness (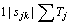 ). Tan et al. [19] later compared the performance of branch and bound, genetic search, simulated annealing and random-start pairwise interchange heuristics for the same problem. Different versions of genetic algorithms have also been proposed (e.g. [19,20]. França et al. [21] proposed a memetic algorithm while Gagne et al. [22] proposed an Ant Colony Optimization (ACO) algorithm for the same problem. Chang et al. [23] proposed a mathematical programming model with logical constraints for the problem
). Tan et al. [19] later compared the performance of branch and bound, genetic search, simulated annealing and random-start pairwise interchange heuristics for the same problem. Different versions of genetic algorithms have also been proposed (e.g. [19,20]. França et al. [21] proposed a memetic algorithm while Gagne et al. [22] proposed an Ant Colony Optimization (ACO) algorithm for the same problem. Chang et al. [23] proposed a mathematical programming model with logical constraints for the problem 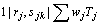 . They also proposed heuristics and conducted computational experiments which revealed that the heuristics can efficiently solve the problem. Wang [24] studied the single-machine scheduling problem with time-dependent learning effect and considerations of setup times with various objective functions based on completion times of jobs.
. They also proposed heuristics and conducted computational experiments which revealed that the heuristics can efficiently solve the problem. Wang [24] studied the single-machine scheduling problem with time-dependent learning effect and considerations of setup times with various objective functions based on completion times of jobs.
This paper first analyzes the problem on a single machine noted as
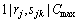 . The proposed randomized heuristic algorithm is presented in this section. The basics of the procedure are presented next. To schedule a set of n on a single machine, we can observe that, from a total of n positions in the schedule, we have to select one position for each job.
. The proposed randomized heuristic algorithm is presented in this section. The basics of the procedure are presented next. To schedule a set of n on a single machine, we can observe that, from a total of n positions in the schedule, we have to select one position for each job. The heuristic proposed here is based on a random insertion strategy, in which random numbers are generated from an equilikely distribution between 1 and n, in order to define the position of a job in the schedule. A certain number of iterations are required so as to improve the initial solution (schedule). The algorithm is described in detail in figure 1.

Figure 1. Random-insertion algorithm for the single-machine problem
In order to analyze computational performance of proposed algorithm, experimental studies were conducted on a PC Pentium bi-processor Dual-Core 1.73 GHz. Exact solution methods were programmed using X-press IVE while the proposed heuristic was programmed using Visual Basic for Applications (VBA) in MS Excel® spreadsheets. Data was generated using a similar structure as proposed by Chu [25] and later extended by Nessah et al. [26] to consider setup times.
Integer processing times were generated from a uniform distribution [1, 100]. Integer release dates were generated using a uniform distribution 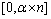 , where n is the number of jobs to be scheduled and
, where n is the number of jobs to be scheduled and 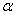 is a real with values 0.6, 1.5 and 3.0. Integer setup times were generated from a uniform distribution
is a real with values 0.6, 1.5 and 3.0. Integer setup times were generated from a uniform distribution 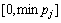 . Five instances for each of value of
. Five instances for each of value of 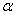 were generated. Problems with 10, 20, 50 or 100 jobs were considered.
were generated. Problems with 10, 20, 50 or 100 jobs were considered.
Experiments were run with equal and unequal release dates. A full factorial experimental design gave a total of 120 testing scenarios. Because of the random behavior of the proposed algorithm, 10 replications for each instance scenario were run and the best sequence (i.e., the sequence with minimum value of the makespan) was registered and compared against the optimum makespan. The first sets of experiments were performed assuming that all jobs are released to the machine at the same time. That is, we are supposing that 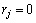 for all jobs.
for all jobs.
The second set of experiments, the same values of both processing and setup times were taken but in addition considering unequal integer non-negative release dates for jobs, that is with 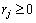 .
.
For the performance analysis, let 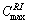 and
and 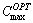 be respectively the makespan obtained using the proposed Random-Insertion heuristic and the optimum makespan. The performance of proposed heuristic was computed using the deviation from the optimal solution as:
be respectively the makespan obtained using the proposed Random-Insertion heuristic and the optimum makespan. The performance of proposed heuristic was computed using the deviation from the optimal solution as:
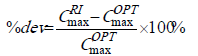
Tables 1 and 2 summarize the results obtained from the experiments for the single-machine environment when all jobs have equal release dates (i.e. respectively when 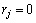 ,
, 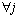 ) and
) and 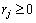 ,
, 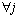 . In both tables,
. In both tables, 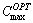 represents the average values of the optimal makespan and
represents the average values of the optimal makespan and 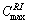 represents the average value of the makespan applying the proposed heuristic. The last column of both tables corresponds to the average value of the deviation from the optimal solution for each set of jobs.
represents the average value of the makespan applying the proposed heuristic. The last column of both tables corresponds to the average value of the deviation from the optimal solution for each set of jobs.
Table 1. Average makespan for experiments with 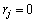 and
and 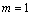
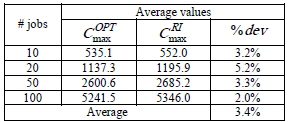
Table 2. Average makespan for experiments with  and
and 
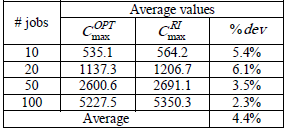
For the case of equal release dates, our algorithm the average deviation from the optimal solution is 3.4%. When unequal release date are present (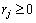 ), the average deviation is 4.4% of the optimal solution. Analyzing the individual instances, in 4% of the cases the heuristic obtained the optimal makespan, while in 29% of the cases the value of the makespan was within a 2% of the optimal value.
), the average deviation is 4.4% of the optimal solution. Analyzing the individual instances, in 4% of the cases the heuristic obtained the optimal makespan, while in 29% of the cases the value of the makespan was within a 2% of the optimal value.
Finally, it is important to note that the running time of the algorithm for small instances (10-job and 20-job instances) was less than 3 seconds, while the time required to run the experiments for large instances was between 20 and 30 seconds for 50-job instances and about 55 seconds for instances with 100 jobs. In comparison with the optimal solution approach, the mathematical model required about 30 minutes and 1 hour to solve small and large instances, respectively.
3. ANALYSIS OF THE CASE OF M IDENTICAL MACHINES IN PARALLEL
In real life, usually discrete manufacturing processes have several m machines in parallel. In this section we extend the algorithm previously proposed to solve the problem. Using the classical notation in Scheduling Theory, the problem under study in noted as 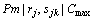 .
.
In the literature the problem under study has been very little studied in the literature. Some related works are cited next. Guinet [27] proposed a mathematical formulation to minimize the makespan and the total completion time of jobs with identical release times (i.e., 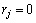 ) for all jobs. Heuristics and meta-heuristics procedures have been proposed for several objective functions, such as due-date related objectives (e.g. [28,29,30] or flowtime related objectives (e.g. [31,32,33]. Guinet [27] also suggested that makespan minimization problem when all jobs have equal release dates (
) for all jobs. Heuristics and meta-heuristics procedures have been proposed for several objective functions, such as due-date related objectives (e.g. [28,29,30] or flowtime related objectives (e.g. [31,32,33]. Guinet [27] also suggested that makespan minimization problem when all jobs have equal release dates (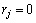 ,
, 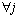 ), the problem is equivalent to the Vehicle Routing Problem (VRP) with service time requirements.
), the problem is equivalent to the Vehicle Routing Problem (VRP) with service time requirements.
The problem with jobs arriving at different release dates has been very little studied in the literature, to the best of our knowledge. Nessah et al. [26] considered the objective of minimizing total completion time of jobs (problem 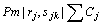 .
.
The problem under study in this paper, 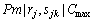 , has only been studied by Kurz and Askin [34] who proposed several heuristics algorithms, including multiple insertion and a genetic algorithm. These authors also derived a data-dependent lower bound for the makespan criterion. Their compared their heuristics between them, but they neither computed the optimal makespan nor compare the performance of their heuristics against the optimum nor the lower bound.
, has only been studied by Kurz and Askin [34] who proposed several heuristics algorithms, including multiple insertion and a genetic algorithm. These authors also derived a data-dependent lower bound for the makespan criterion. Their compared their heuristics between them, but they neither computed the optimal makespan nor compare the performance of their heuristics against the optimum nor the lower bound.
3.1. Proposed algorithm modified
Our algorithm described in section 2 for the single-machine case can be easily modified for application in the parallel machine environment. The first modification consists on computing the number of jobs that can scheduled on each machine. Then, jobs are randomly selected and assigned to machines respecting the workload balance defined. The modified algorithm is described in detail in figure 2.

Figure 2. Random-insertion algorithm for the identical parallel machines problem
3.2. Experiments and results
A computational study was also performed using the same random-generated data as described in section 2.2. We considered here configurations with 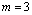 and
and 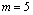 identical machines in parallel. As for the single-machine case, because of the random behavior of the proposed algorithm, 10 replications for each instance scenario were run and the best sequence (i.e., the sequence with minimum value of the makespan) was registered and compared against the optimum makespan.
identical machines in parallel. As for the single-machine case, because of the random behavior of the proposed algorithm, 10 replications for each instance scenario were run and the best sequence (i.e., the sequence with minimum value of the makespan) was registered and compared against the optimum makespan.
As explained previously, the NP-completeness of this problem unable us to obtain optimal solutions without excessive computational costs even for small instances [34]. A lower bound on the makespan can be found by looking at the minimum preemptive schedule makespan [35]. This lower bound, however, can be very poor, especially in cases with a high range of processing times [34].
As explained previously, Kurz and Askin [34] derived a preemptive-type lower bound on the makespan for each of the individual data sets using the actual data. These authors showed that their lower bound performs well. This lower bound is thus computed as:
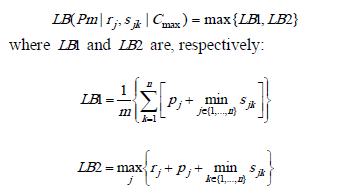
Results of our experimental study are hence compared against this lower bound. Let 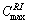 be the makespan obtained using the proposed heuristic and let
be the makespan obtained using the proposed heuristic and let 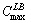 be the value of the lower bound. Hence, the performance of the proposed heuristic was computed as the deviation from such lower bound as:
be the value of the lower bound. Hence, the performance of the proposed heuristic was computed as the deviation from such lower bound as:
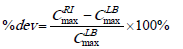
Tables 3 and 4 present the summary of results, respectively, with equal and unequal jobs release dates. From these results, we can observe that the algorithm performs well, with reference to the percentage deviation from the lower bound of the makespan: the average deviation, regardless of the number of jobs, is 9.9% with equal release dates and 12.2% for the case with unequal release dates. These results are the first results in literature that show the performance of a heuristic in comparison against a known lower bound.
Table 3. Results for parallel machines experiments with 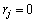

Table 4. Results for parallel machine experiments with 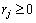

In terms of the computational costs, the higher the number of jobs, the higher the time to find a solution. For the large instance in our tests (100 jobs), the computational time was never higher than 12 seconds. For 10-jobs and 20-jobs instances, the CPU time was less than 1 second.
4. CONCLUSIONS
This paper considered the problem of scheduling jobs on both a single-machine and identical parallel machines environments subject to release dates and setup times. Setup times , de fined in general as the time required to prepare the necessary resource to perform a job, add complexity for the analysis of scheduling problems. Since the problem is NP-hard, a heuristic algorithm was proposed.
The strategy for scheduling is based on a random insertion of jobs in the schedule.
Computational experiments were performed using random-generated data following similar procedures as in literature. Two main cases were considered. The first test was carried out with jobs having equal release dates. The second set of tests considered non negative release dates (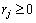 ). Compared against the optimal solution, the proposed heuristic performed very well giving schedules with a makespan value no greater than the 10% of the optimum. In average, the proposed procedure was between about 2% and 6% of the optimal solution.
). Compared against the optimal solution, the proposed heuristic performed very well giving schedules with a makespan value no greater than the 10% of the optimum. In average, the proposed procedure was between about 2% and 6% of the optimal solution.
The computational time was less than 2 seconds for small instances, and never higher than 1 minute for large instances (100 jobs). An extension to the identical parallel machine environment was also considered. Results of the computational experiments showed that our algorithm performs well in comparison with the lower bound of the makespan value. The average deviation from this bound was 9.9% with 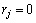 and 12.2% for the case with
and 12.2% for the case with 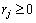 , regardless of the number of jobs.
, regardless of the number of jobs.
ACKNOWLEDGEMENTS
This work was performed under research project CEA-24-2008 supported by Research Funds from Universidad de La Sabana, Chía, Colombia. Authors wish to acknowledge the anonymous reviewers for their comments that allow improving the presentation of the paper.
REFERENCES
[1] PINEDO, M. 2008. Scheduling: Theory, Algorithms, and Systems. Springer. [ Links ]
[2] OZGUR, C.O., BROWN, J.R. 1995. A two-stage traveling salesman procedure for the single machine sequence-dependent scheduling problem. Omega, 23, 205-219. [ Links ]
[3] ALLAHVERDI, A., SOROUSH, H.M. 2008. The significance of reducing setup times/setup costs. European Journal of Operational Research, 187, 978-984. [ Links ]
[4] FLYNN, B.B. 1987. The effects of setup time on output capacity in cellular manufacturing. International Journal of Production Research, 25, 1761-1772. [ Links ]
[5] KOGAN, K., LEVNER, E. 1998. A polynomial algorithm for scheduling small-scale manufacturing cells served by multiple robots. Computers & Operations Research, 25, 53-62. [ Links ]
[6] KRAJEWSKI, L.J., KING, B.E., RITZMAN, L.P., WONG, D.S. 1987. Kanban, MRP and shaping the manufacturing environment. Management Science, 33, 39-57. [ Links ]
[7] LIU, C.Y., CHANG, S.C. 2000. Scheduling flexible flow shops with sequence-dependent setup effects. IEEE Transactions on Robotics and Automation, 16, 408-419. [ Links ]
[8] TROVINGER, S.C., BOHN, R.E. 2005. Setup time reduction for electronics assembly: Combining simple (SMED) and IT-based methods. Production and Operations Management, 14, 205-217. [ Links ]
[9] ALLAHVERDI, A., GUPTA, J.N.D., ALDOWAISAN, T. 1999. A review of scheduling research involving setup considerations. Omega, 27, 219-239. [ Links ]
[10] ALLAHVERDI, A., NG, C.T., CHENG, T.C.E., KOVALYOV, M.Y. 2008. A survey of scheduling problems with setup times or costs. European Journal of Operational Research, 187, 985-1032. [ Links ]
[11] ZHU, X., WILHELM, W.E. 2006. Scheduling and lot sizing with sequence-dependent setup: A literature review. IIE Transactions, 38, 987-1007. [ Links ]
[12] GILMORE, P.C., GOMORY, R.E. 1964. Sequencing a one-state variable machine: a solvable case of the traveling salesman problem. Operations Research, 12, 655-679. [ Links ]
[13] PRESBY, J.T., WOLFSON, M.L. 1967. An algorithm for solving job sequencing problems. Management Science, 13, B454-B464. [ Links ]
[14] BIANCO, L., RICCIARDELLI, S., RINALDI, G., SASSANO, A. 1988. Scheduling tasks with sequence-dependent processing times. Naval Research Logistics, 35, 177-184. [ Links ]
[15] HE, W., KUSIAK, A. 1992. Scheduling manufacturing systems. Computers in Industry, 20, 163-175. [ Links ]
[16] BARNES, J.W., VANSTON, L.K. 1981. Scheduling jobs with linear delay penalties and sequence dependent setup times and release dates. Operations Research, 29, 146-154. [ Links ]
[17] UZSOY, R., LEE, C.Y., MARTIN-VEGA, L.A. 1992. Scheduling semiconductor test operations: Minimizing maximum lateness and number of tardy jobs on a single machine. Naval Research Logistics, 39, 369-388. [ Links ]
[18] TAN, K.C., NARASIMHAN, R. 1997. Minimizing tardiness on a single processor with sequence-dependent setup times. Omega, 25, 619-634. [ Links ]
[19] TAN, K.C., NARASIMHAN, R., RUBIN, P.A., RAGATZ, G.L. 2000. A comparison of four methods for minimizing total tardiness on a single processor with sequence dependent setup times. Omega, 28, 313-326. [ Links ]
[20] ARMENTANO, V.A., MAZZINI, R. 2000. A genetic algorithm for scheduling on a single machine with with set-up and due dates. Production Planning and Control, 11, 713-720. [ Links ]
[21] FRANÇA, P.M., MENDES, A., MOSCATO, P. 2001. A memetic algorithm for the total tardiness single machine scheduling problem. European Journal of Operational Research, 132, 224-242. [ Links ]
[22] GAGNE, C., PRICE, W.L., GRAVEL, M. 2002. Comparing an ACO algorithm with other heuristics for the single machine scheduling problem with sequence-dependent setup times. Journal of the Operational Research Society, 53, 895-906. [ Links ]
[23] CHANG, T.Y., CHOU, F.D., LEE, C.E. 2004. A heuristic algorithm to minimize total weighted tardiness on a single machine with release dates and sequence-dependent setup times. Journal of the Chinese Institute of Industrial Engineering, 21, 289-300. [ Links ]
[24] WANG, J.B. 2008. Single-machine scheduling with past-sequence-dependent setup times and time-dependent learning effect. Computers & Industrial Engineering, 55, 584-591. [ Links ]
[25] CHU, C. 1992. Efficient heuristics to minimize total flow time with release dates. Operations Research Letters, 12, pp. 321-330. [ Links ]
[26] NESSAH, R., CHU, C., YALAOUI, F. 2007. An exact method for problem. Computers & Operations Research, 34, 2840-2848. [ Links ]
[27] GUINET, A. 1993. Scheduling sequence-dependent jobs on identical parallel machines to minimize completion time criteria. International Journal of Production Research, 31, 1579-1594. [ Links ]
[28] BILGE, U., KIRAC, F., KURTULAN, M., PEKGUN, P. 2004. A tabu search algorithm for parallel machine total tardiness problem. Computers & Operations Research, 31, 397-414. [ Links ]
[29] PFUND, M., FOWLER, J.W., GADKARI, A., CHEN, Y. 2008. Scheduling jobs on parallel machines with setup times and ready times. Computers & Industrial Engineering, 54, 764-782. [ Links ]
[30] SIVRIKAYA-SERIFOGLU, F., ULUSOY, G. 1999. Parallel machine scheduling with earliness and tardiness penalties. Computers & Operations Research, 26, 773-787. [ Links ]
[31] ABDEKHODAEE, A.H., WIRTH, A. 2002. Scheduling parallel machines with a single server: some solvable cases and heuristics, Computers & Operations Research, 29, 295-315. [ Links ]
[32] ABDEKHODAEE, A.H., WIRTH, A., GAN, H.S. 2004. Equal processing and equal setup time cases of scheduling parallel machines with a single server. Computers & Operations Research, 31, 1867-1889. [ Links ]
[33] WEBSTER, S., AZIZOGLU, M. 2001. Dynamic programming algorithms for scheduling parallel machines with family setup times. Computers & Operations Research, 28, 127-137. [ Links ]
[34] KURZ, M.E., ASKIN, R.G. 2001. Heuristic scheduling of parallel machines with sequence-dependent set-up times. International Journal of Production Research, 39, 3747-3769. [ Links ]
[35] McNAUGHTON, R. 1959. Scheduling with deadlines and loss functions. Management Science, 6, 1-12. [ Links ]














