Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.77 n.164 Medellín out./dez. 2010
MATRICES DE RIGIDEZ Y DE CARGA DE PRIMER Y SEGUNDO ORDEN DE UNA VIGA-COLUMNA ORTOTRÓPICA CON CONEXIONES SEMIRRÍGIDAS: II) EJEMPLOS
FIRST AND SECOND ORDER STIFFNESS AND LOAD MATRICES OF AN ORTHOTROPIC BEAM COLUMN WITH SEMIRIGID CONNECTIONS: II) EXAMPLES
J. DARIO ARISTIZABAL-OCHOA
ProfesorTitular Generación 125-Años, Facultad de Minas, Universidad Nacional, Medellín-Colombia, jdaristi@unal.edu.co
Recibido para revisar Mayo 19 de 2009, aceptado Octubre 8 de 2009, versión final Noviembre 15 de 2009
RESUMEN: Las matrices de rigidez y de carga de primer y segundo orden de una viga-columna de Timoshenko ortotrópica de sección transversal simétrica con conexiones semirrígidas incluyendo los efectos de la carga axial en los extremos (tracción o compresión) y de las fuerzas cortantes a lo largo del elemento fueron deducidas en el primer artículo. El modelo de Haringx descrito por Timoshenko y Gere (1961) fue adoptado en la formulación de las matrices. Ambas matrices serán utilizadas en los análisis elásticos de estabilidad, de primer y de segundo orden de estructuras aporticadas con elementos viga-columna de Timoshenko de sección transversal simétrica con conexiones rígidas, semirrígidas y simples en los cinco adjuntos en este artículo. Estudios analíticos indican que la carga de pandeo y la rigidez de estructuras aporticadas son reducidas por efecto de la deformación por cortante a lo largo de cada elemento. Además, el fenómeno de pandeo bajo fuerzas de tracción en elementos con rigidez a cortante relativamente baja es incluido en las ecuaciones propuestas. El pandeo por tracción no debe ser ignorado en el análisis de estabilidad de elementos viga-columna con rigidez a cortante GAs del mismo orden de magnitud que EI/h2. La validez de ambas matrices es verificada con soluciones disponibles de análisis de estabilidad y de comportamiento elástico geométrico no lineal de estructuras viga-columna. Se incluyen cinco ejemplos que demuestran la eficiencia del método propuesto y de las matrices correspondientes.
PALABRAS CLAVE: Pandeo, Columnas; Tipos de construcción; Pórticos; Efectos P-D; Deformaciones por cortante; Análisis de segundo orden; Conexiones semirrígidas; Estabilidad; Pandeo por tracción.
ABSTRACT: The first- and second-order stiffness and load matrices of an orthotropic Timoshenko beam-column of symmetric cross section with semirigid connections including the effects of end axial loads (tension or compression) and shear deformations along the member are derived in the first article. The “modified” stability approach based on Haringx´s model described by Timoshenko and Gere (1961) is utilized in all matrices. Both matrices are used in the stability, first- and the second-order elastic analyses of framed structures made of Timoshenko beam-columns with rigid, semirigid and simple connections of symmetric cross sections in the five examples included in this article. Analytical studies indicate that the buckling load and the stiffness of framed structures are reduced by the shear deformations along the members. In addition, the phenomenon of buckling under axial tension forces in members with relatively low shear stiffness is captured by the proposed equations. Tension buckling must not be ignored in the stability analysis of beam-columns with shear stiffness GAs of the same order of magnitude as EI/h2. The validity of both matrices is verified against available solutions of stability analysis and nonlinear geometric elastic behavior of beam-column structures. Five examples are included that demonstrate the effectiveness of the proposed method and corresponding matrices.
KEYWORDS: Buckling; Columns; Construction Types; Computer applications; Frames; Loads; P-D Effects; Shear deformations; Second-order analysis; Semirigid Connections; Stability; Tension Buckling.
1. INTRODUCCIÓN
El objetivo principal de esta publicación es presentar las posibles usos de las matrices de rigidez y de carga de primer y de segundo orden de un elemento viga-columna ortotrópica de Timoshenko con conexiones semirrígidas y de sección transversal simétrica utilizando el modelo de Haringx. Los efectos geométricos no lineales previamente descritos en el primer artículo son incluidos en los coeficientes de rigidez axial y transversal y el vector de carga.
2. EJEMPLOS
2.1 Ejemplo 1. Matrices de rigidez y de carga para una viga-columna ortotrópica pultruida (FRP)
Determine los principales coeficientes de rigidez (i.e., k11, k21, k22 y k55) para una viga-columna I ortotrópica pultruida (FRP) de 200´200´10 descrita por Roberts (2002) para cargas axiales: P=40 kN (compresión) y P=-40kN (tracción) con las siguientes propiedades: h= 8,500 mm ; A= 5,800 mm2; ExIx= 7.85´108 KN-mm2; EyIy= 2.48´108 KN-mm2; GxAsx= 5,340 KN; GyAsy=6,710 KN; GeJe=8.56´105 KN-mm2; módulos elásticos Ex= 18.863 KN/mm2, Ey= 18.633 KN/mm2, Ez= 17 KN/mm2, Gx= 2.671 KN/mm2, Gy=2.012 KN/mm2, y Ge= 4.428 KN/mm2. También determine los momentos fijos para una carga uniformemente distribuida w aplicada a todo lo largo de la luz h y para una carga concentrada W aplicada en la mitad de la luz en cada uno de los planos principales. Suponga que rax= ray=rbx= rby=1 alrededor de los ejes locales x y y, respectivamente.
Solución:
Los coeficientes principales de rigidez y los momentos fijos en los extremos se presentan a continuación.
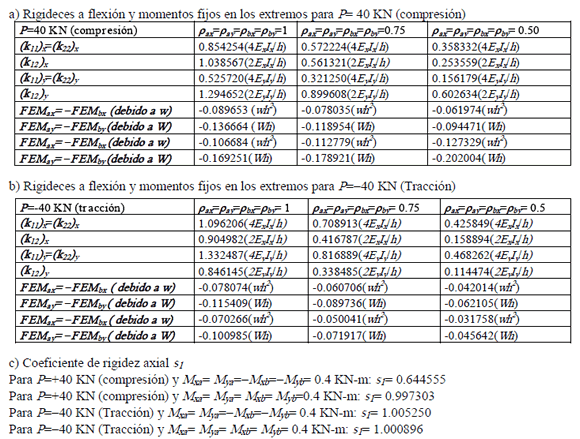
2.2 Ejemplo 2. Análisis de segundo orden de una columna en y sujeta a varias cargas en el extremo superior
Determine las ecuaciones carga-deflexión de segundo orden para la columna en voladizo AB mostrada en la figura 1. Compare las expresiones resultantes con las deducidas por Timoshenko y Gere (1961, páginas 5 y 13) para una columna de Bernoulli-Euler en voladizo perfectamente empotrada (rb= b= 1).
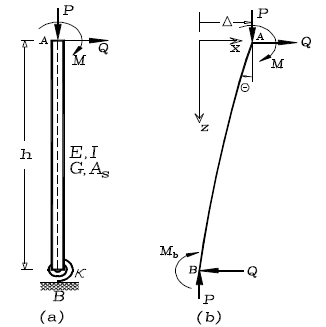
Figura 1 EJEMPLO 2: Análisis de segundo orden de una columna en voladizo: (a) modelo estructural; y (b) forma deflectada y fuerzas en los extremos
Figure 1 EXAMPLE 2: Second -Order Analysis of a Cantilever Column: (a) Structural Model and (b) Deflected shape and end forces
Solución: En este ejemplo ra= 1 y rb= r y la rotación y la deflexión lateral en el extremo superior (q, D) pueden ser obtenidas utilizando las ecuaciones (15)-(17) del primer artículo como sigue:
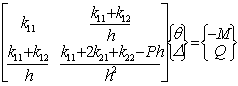 (1)
(1)
Por lo tanto: 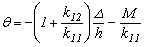 (2)
(2)
y 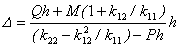 (3)
(3)
Donde: 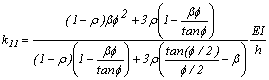 ;
;
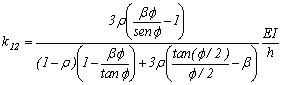 ; y
; y 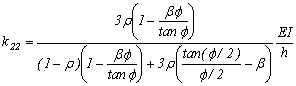 para
para 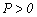 (compresión)
(compresión)
La ecuación (3) puede ser reducida a: 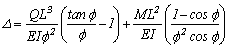 la cual es idéntica a la superposición de las ecuaciones (g) y (1-33) presentadas por Timoshenko y Gere (1961, páginas 5 y 14) para el caso de una columna Bernoulli-Euler en voladizo perfectamente empotrada (i.e., rb= b= 1) bajo la carga lateral Q , carga axial P y el momento flector M, respectivamente. El análisis a grandes deflexiones (vertical y horizontal) y el comportamiento post-pandeo de una columna de Timoshenko en voladizo sujetas a cargas en el extremo superior es discutido por Aristizabal-Ochoa (2007).
la cual es idéntica a la superposición de las ecuaciones (g) y (1-33) presentadas por Timoshenko y Gere (1961, páginas 5 y 14) para el caso de una columna Bernoulli-Euler en voladizo perfectamente empotrada (i.e., rb= b= 1) bajo la carga lateral Q , carga axial P y el momento flector M, respectivamente. El análisis a grandes deflexiones (vertical y horizontal) y el comportamiento post-pandeo de una columna de Timoshenko en voladizo sujetas a cargas en el extremo superior es discutido por Aristizabal-Ochoa (2007).
2.3 Ejemplo 3. Estabilidad de una Viga-Columna de dos luces con un Soporte Elástico Intermedio
Determine la carga crítica de pandeo de la viga-columna de dos luces mostrada en la figura 2. Asuma que los elementos 1 y 2 están inicialmente horizontales con propiedades (GAs), (EI)1, L1 y (GAs)2, (EI)2, L2, respectivamente. También suponga que las cargas aplicadas aP y P permanecen siempre horizontales y son aplicadas en los nodos 2 y 3, respectivamente. Incluya los efectos de la rigidez transversal en el apoyo intermedio 2. Compare los resultados con los presentados por Timoshenko y Gere (1961, pp. 70 y 99) cuando el elemento está compuesto de dos elementos viga-columna Euler-Bernoulli.
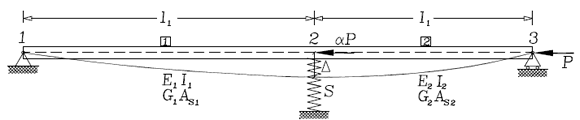
Figura 2. EJEMPLO 3. Análisis de estabilidad de una viga-columna de dos luces con un apoyo elástico intermedio: modelo estructural y forma deflectada
Figure 2. EXAMPLE 3. Stability analysis of a two-span beam with an intermediate elastic support: structural model and deflected shape
Solución:
Sabiendo que para el elemento AB que ra= 0, rb= 1 y para el elemento BC ra= 1, rb= 0, los coeficientes de rigidez utilizando las expresiones (14)-(16) para P> 0 y 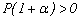 son como sigue:
son como sigue:
Rigidez a flexión del elemento AB en B: 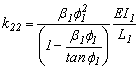 y
y 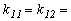 0
0
Rigidez a flexión del elemento BC en B: 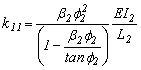 y
y 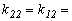 0
0
Donde: 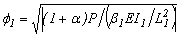 ;
;
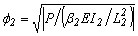 ;
;
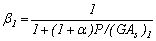 ;
; 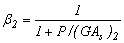 .
.
Por lo tanto:
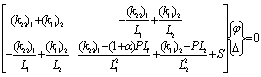 (4)
(4)
Realizando el determinante de la matriz 2´2 en la ecuación (4) se puede determinar la ecuación característica y de la cual se pueden calcular las cargas de pandeo. Por ejemplo, para el caso particular de EI1= EI2 y L1= L2= L/2 y S= 0, la ecuación característica del sistema homogéneo (28) se reduce a:
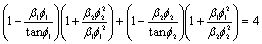 (5)
(5)
La ecuación (5) arroja resultados idénticos a los obtenidos por Timoshenko y Gere (1961, p. 99 ecuación 2-42) para un elemento simplemente apoyado compuesto por un elemento viga-columna Euler-Bernoulli (con b1=b2= 1) con cargas de compresión en los nodos 2 y 3.
Otro caso interesante es cuando el valor de S se hace muy grande haciendo que 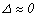 , y entonces la ecuación característica es reducida al primer término de la ecuación (4) como sigue:
, y entonces la ecuación característica es reducida al primer término de la ecuación (4) como sigue:
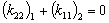 ó
ó
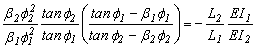 (6)
(6)
La ecuación (6) arroja resultados idénticos a los obtenidos por Timoshenko y Gere [1961, p. 67 ecuación (b)] para una viga-columna Euler-Bernoulli de dos luces (con b1=b2=1) con cargas de compresión en los nodos 1 y 3.
La figura 3 muestra una serie de diagramas de interacción de P/(EI/L2)-versus-aP/(EI/L2) para diferentes valores de S/(EI/L3) todos obtenidos utilizando la ecuación (4) para el caso particular de L1= L2= L/2, (GAs)1=(GAs)2= ∞ y (EI)1= (EI)2= EI. La figura 4 muestra la variación de la carga de pandeo de una viga simplemente apoyada con la rigidez S del soporte elástico intermedio localizado en la mitad de la luz para diferentes valores de GAs/(EI/L2).
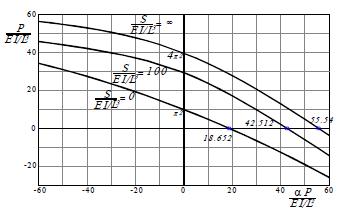
Figura 3. Diagramas de interacción P/(EI/L2)-versus-aP/(EI/L2) para la viga-columna de dos luces del ejemplo 3 [para el caso particular de L1 = L2 = L/2, (GAs)1=(GAs)2= ∞ y (EI)1= (EI)2= EI] con un Apoyo elástico Intermedio con S/(EI/L3)= ∞, 100, y 0
Figure 3. Interaction Diagrams P/(EI/L2)-vs-aP/(EI/L2) for the two-span beam-column of example 3 [for the particular case of L1= L2 = L/2, (GAs)1=(GAs)2= ∞ and (EI)1= (EI)2= EI] with an intermediate elastic support with S/(EI/L3)= ∞, 100, and 0
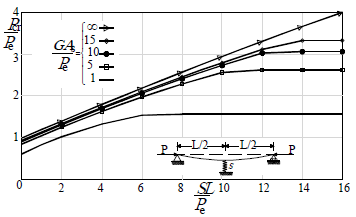
Figura 4. Variaciones de la carga critica de una viga-[esta curva es idéntica a la presentada por Timoshenko y Gere (1961, p. 73)]. columna simplemente apoyada con la rigidez del apoyo elástico intermedio S
Figure 4. Variations of the critical loads of a simple supported beam column with the stiffness of the intermediate elastic support S
Nótese que: 1) los valores indicados en la figura 3 correspondientes a la curva con S= 0 son idénticos a los presentados por Timoshenko y Gere (1961, p. 100 Tablas 2-6 para n= 1); 2) la capacidad de carga de pandeo de la viga-columna es afectada significativamente no solo por la ubicación cortante de los elementos como lo muestran las curvas de la figura 4; y 3) la curva correspondiente a GAs/(EI/L2)= ∞ en la figura 4 muestra que la carga crítica se incrementa en aproximadamente la misma proporción que S y la rigidez del soporte medio sino también por la magnitud de la rigidez a
2.4 Ejemplo 4. Análisis de la estabilidad de un pórtico plano con deriva lateral parcialmente inhibida sujeto a cargas axiales
Determine las cargas de pandeo del pórtico plano (figura 5) con deriva lateral parcialmente inhibida. Los factores de fijeza ρ de las conexiones semirrígidas viga a columna y el de la columna a la fundación son indicados en la figura 5. Suponga que: 1) los elementos horizontales y verticales tienen cada uno las siguientes propiedades [(EI)1, (GAs)1, h1], [(EI)2, (GAs)2, h2] y [(EI)3, (GAs)3,, L], respectivamente; y 2) las cargas axiales aplicadas P y aP son siempre verticales. Incluya los efectos de la rigidez S de la riostra lateral en el nodo 2 y desprecie los efectos de las deformaciones axiales en todos los miembros. Compare estos resultados con los presentados por Salmon y Johnson (1996) para un pórtico simétrico compuesto de elementos Euler-Bernoulli cuando las conexiones viga a columna son rígidas (i.e., ρ1= ρ2= 1) y las bases de las columnas están perfectamente articuladas (i.e., ρ3=ρ4= 0) y a= 1. Discuta también la estabilidad del pórtico bajo fuerzas axiales de tracción.
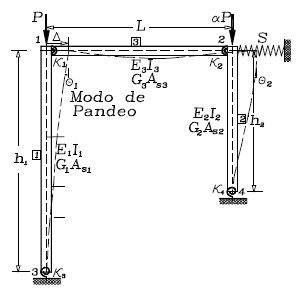
Figura 5. EJEMPLO 4: Análisis de estabilidad de un pórtico plano asimétrico con deriva lateral parcialmente inhibida: modelo estructural, cargas, grados de libertad y elemento reflectado
Figure 5. EXAMPLE 4: Stability Analysis of an unsymmetrical frame with lateral sway partially inhibited: structural model, loads, degrees of freedom on deflected member.
Solución:
En este caso particular hay tres incógnitas 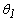 ,
, 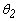 y D como muestra la figura 5. Aplicando equilibrio, se obtiene el siguiente sistema homogéneo 3´3
y D como muestra la figura 5. Aplicando equilibrio, se obtiene el siguiente sistema homogéneo 3´3
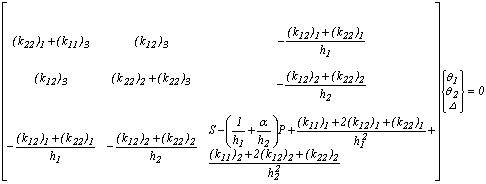 (7)
(7)
Donde:
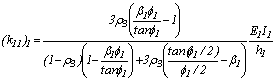 ;
;
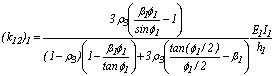 ;
; 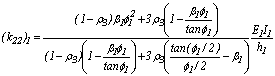 ;
;
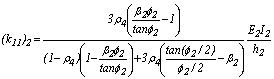 ;
;
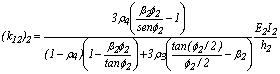 ;
; 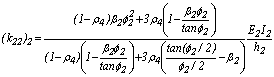 ;
;
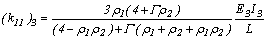 ;
;
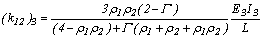 y
y
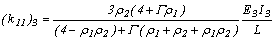
Haciendo el determinante de la matriz 3´3 de la ecuación (7) igual a cero se determina la ecuación característica de la cual las cargas de pandeo pueden ser calculadas. En el caso particular de un pórtico simétrico no arriostrado con columnas Bernoulli-Euler y viga con EI1=EI2, b1=b2=b3= 1, h1=h2= h, a= 1, r1=r2=1, r3= r4=0, S= G= 0, y suponiendo que q1= q2 la ecuación característica de (7) es reducida a:
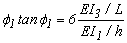 (8)
(8)
Otro caso interesante es cuando el valor de S toma valores muy grandes haciendo que D» 0 (i.e., para un marco con deriva lateral inhibida), entonces la ecuación característica se reduce a las primeras dos filas y columnas de la ecuación (7):
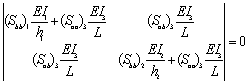 (9)
(9)
En el caso particular de un pórtico simétrico con columnas Bernoulli-Euler y viga con EI1= I2, b1= b2= b3= 1, h1= h2= h, a= 1, r1= r2= 1, r3= r4= 0, G= 0 y suponiendo que q1=-q2 la ecuación característica (9) puede ser reducida a:
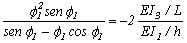 (10)
(10)
Las ecuaciones (8) y (10) son idénticas a las ecuaciones (14-2-30) y (14-2-18) presentadas por Salmon y Johnson (1996, páginas 900-912) para marcos simétricos arriostrados y no arriostrados, respectivamente. Se debe enfatizar que la ecuación (32) solo es capaz de capturar los modos anti-simétricos de pandeo del pórtico simétrico no arriostrado (dado que se supuso que q1= q 2). Igualmente, la ecuación (10) solo es capaz de capturar los modos simétricos de pandeo del pórtico simétrico arriostrado (dado que se supuso que q1= -q2).
La figura 6 muestra los tres primeros valores propios obtenidos usando la ecuación característica (7) y los dos primeros obtenidos usando la ecuación (8). Por lo tanto, el método propuesto es más potente dado que es capaz de capturar todos los modos de pandeo incluyendo aquellos bajo fuerzas axiales de tracción (como se mostró en los Ejemplos 2 y 3).
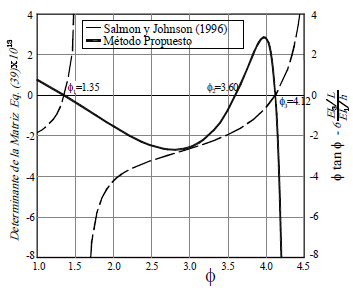
Figura 6. Comparación de los resultados para un pórtico simétrico con deriva lateral inhibida usando el método propuesto y una fórmula simplificada de Salmon y Johnson (1996)
Figure 6. Comparison of results for a symmetrical frame with lateral sway inhibited using the proposing method and a simplified formula after Salmon y Johnson (1996)
2.4 Ejemplo 5. Análisis de segundo orden de un pórtico plano con conexiones semirrígidas
Determine las fuerzas internas de segundo orden de cada elemento para el pórtico plano mostrado en la figura 7. El pórtico está hecho de elementos viga-columna ortotrópica pultruida FRP) descrita en el Ejemplo 1 con la flexión alrededor del eje x. Suponga que: A= 5800 mm2; ExIx= 7.85´108 KN-mm2; GxAsx= 5340 KN; modulo de elasticidad Ex= 18.863 KN/mm2, Ez= 17 KN/mm2 y Gx= 2.671 KN/mm2. Incluir los efectos de la deformación por cortante y también los efectos de los momentos flectores sobre la rigidez axial.
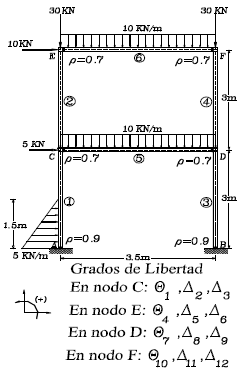
Figura 7. EJEMPLO 5: Análisis de primer y segundo orden de un pórtico no arriostrado con conexiones semirrígidas: modelo estructural y grados de libertad
Figure 7. EXAMPLE 5: First and second order analysis of an unbraced frame with semirigid connections: structural model and degrees of freedom
Solución:
Los diagramas de cuerpo libre de cada elemento del pórtico mostrando al final las fuerzas internas en los extremos obtenidas del análisis de primer orden son mostrados en la figura 8a.
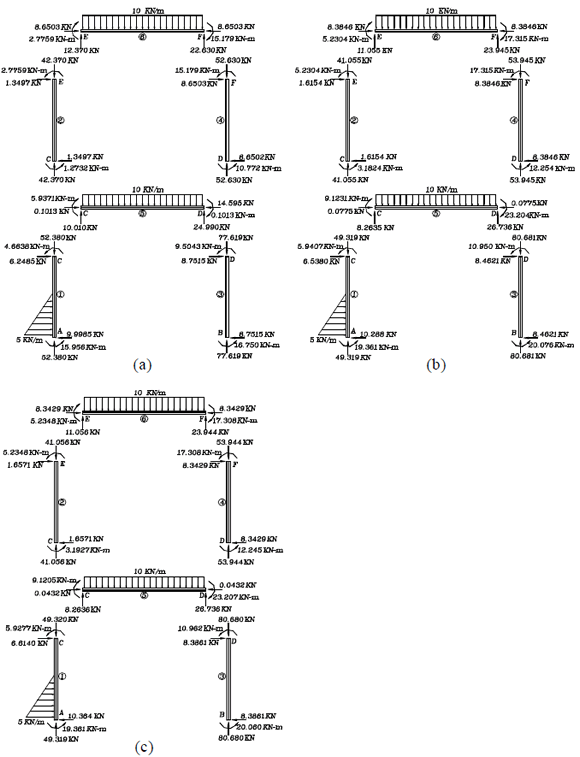
Figura 8. EJEMPLO 5: (a) Fuerzas y momentos de primer orden en los extremos, (b) Fuerzas y momentos de segundo orden en los Extremos (Iteración 1); y (c) Fuerzas y momentos de segundo orden en los extremos (segunda y última iteración)
Figure 8. EXAMPLE 5: (a) First-order end moments and forces, (b) Second-order end forces and moments (first iteration); and (c) Second-order end forces and moments (second and final iteration)
En la primera iteración del análisis de segundo orden, la carga axial aplicada y la carga axial resultante de las fuerzas internas del pórtico mostradas en la figura 8a son consideradas. La matriz de rigidez global y el vector de carga del sistema de 12-DOF (ver figura 7) de cada iteración se resumen a En consecuencia, el análisis de primer orden es reducido a la solución del siguiente sistema de ecuaciones:
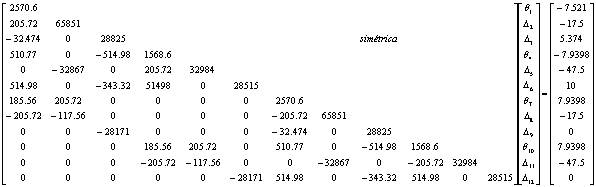 (11)
(11)
Cuya solución (rotaciones y desplazamientos) es θ1=-0.020630 rad; Δ2=-0.0016 m; Δ3= 0.0534 m ; θ4=-0.017756 rad; Δ5= -0.0029 m ; Δ6=0.1149 m; θ7=-0.0162 rad; Δ8=-0.0024 m; Δ9= 0.0534 m ; θ10=-0.007795 rad; Δ11=-0.0040 m; y Δ12= 0.1146 m .
Análisis de segundo orden
. Primera Iteración: usando la fuerza axial y momentos obtenidos del análisis de primer orden los coeficientes de rigidez para cada elemento son los siguientes:
Elemento 1: P= 52.3805 KN; k11= 798.493 KN-m; k12= 357.954 KN-m; k22= 879.783 KN-m; y s1= 0.953118.
Elemento 2: P= 42.3700 KN; k11= 903.710 KN-m; k12= 401.854 KN-m; k22= 903.710 KN-m; y s1= 0.998774.
Elemento 3: P= 77.6195 KN; k11= 791.479 KN-m; k12= 362.222 KN-m; k22= 870.410 KN.m; y s1= 0.979907.
Elemento 4: P=52.6270 KN; k11= 900.141 KN-m; k12= 403.603 KN-m; k22= 900.141 KN-m; y s1= 0.982873.
Elemento 5: P= 0.101274 KN; k11= 510.716 KN-m; k12= 161.828 KN-m; k22= 510.716 KN-m; y s1= 0.019709.
Elemento 6: P= 8.65027 KN; k11= 508.861 KN-m; k12= 163.010 KN-m; k22= 508.861 KN-m; y s1= 0.704112.
La primera iteración es reducida a la solución de la ecuación matricial (12):
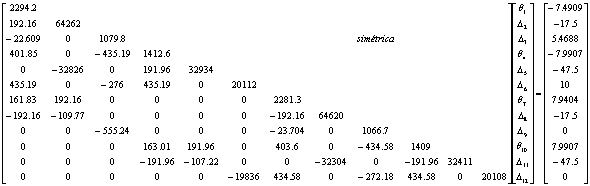 (12)
(12)
La solución (rotaciones y desplazamientos) de la ecuación (12) es:
θ1=-0.026878 rad; Δ2=-0.0016 m; Δ3= 0.0728 m ; θ4=-0.0228 rad; Δ5=-0.0028 m; Δ6=0.1570 m; θ7=-0.021721 rad; Δ8=-0.0025 m; Δ9= 0.0727 m ; θ10=-0.011530 rad; Δ11=-0.0042 m; y Δ12=0.1565 m.
. Segunda iteración:
Elemento 1: P= 49.3187 KN; k11= 799.334 KN-m; k12= 357.442 KN-m; k22= 880.907 KN-m; y s1= 0.931196.
Elemento 2: P= 41.0552 KN; k11= 904.165 KN-m; k12= 401.631 KN-m; k22= 904.165 KN-m; y s1= 0.996831.
Elemento 3: P= 80.6813 KN; k11= 790.617 KN-m; k12= 362.746 KN-m; k22= 869.260 KN-m; y s1= 0.970807.
Elemento 4: P= 53.9448 KN; k11= 899.681 KN-m; k12= 403.828 KN-m; k22= 899.681 KN-m; y s1= 0.978233.
Elemento 5: P= 0.077476 KN; k11= 510.721 KN-m; k12= 161.825 KN-m; k22= 510.721 KN.m; y s1= 0.014344.
Elemento 6: P= 8.384626 KN; k11= 508.919 KN-m; k12= 162.973 KN-m; k22= 508.919 KN.m; y s1= 0.693990.
La segunda iteración es reducida a la solución de la ecuación matricial (13):
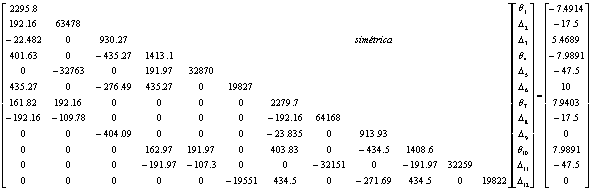 (13)
(13)
La solución (rotaciones y desplazamientos) de la ecuación (13) es:
θ1=-0.026867 rad; Δ2=-0.002 m; Δ3= 0.073 m; θ4=-0.022803 rad; Δ5=-0.003 m; Δ6= 0.157 m; θ7=-0.021724 rad; Δ8=-0.003 m; Δ9= 0.073 m ; θ10=-0.011514 rad; Δ11=-0.004 m; y Δ12= 0.157
Ya que la variación de los desplazamientos entre la primera y segunda iteración es relativamente pequeña (< 0.5%) una iteración adicional se consideraría innecesaria. Nótese que la deflexión lateral y los momentos flectores en los extremos aumentan significativamente (por encima del 36% y 21% de sus valores iniciales, respectivamente) causados por los cinco efectos geométricos no lineales mencionados en la introducción.
3. RESUMEN Y CONCLUSIONES
Las matrices de rigidez de primer y segundo orden y los momentos fijos en los extremos de una viga-columna de Timoshenko ortotrópica con conexiones semirrígidas incluyendo los efectos combinados de flexión más las deformaciones por cortante y la componente de la cortante inducida por la fuerza axial aplicada (Modelo de Haringx) desarrolladas en el primer artículo son utilizadas en cinco ejemplos incluidos en esta segunda publicación.
Resultados analíticos indican que la estabilidad y la respuesta de segundo orden de estructuras aporticadas no solo están afectadas por la magnitud de las cargas axiales en sus elementos, la magnitud y localización de las restricciones contra deriva lateral, y el grado de fijeza de las conexiones, sino también por la reducción en la rigidez axial de cada elemento causada por los momentos flectores y las deformaciones por cortante a lo largo de los miembros. Las deformaciones por cortante incrementan las deflexiones laterales de estructuras aporticadas y reducen las cargas críticas axiales.
Los efectos de las deformaciones por cortante y los efectos P-D de segundo orden deben ser considerados en el análisis de vigas-columna con área efectiva a cortante relativamente baja (como columnas hechas en celosía) o con módulo a cortante G bajo (como soportes elastoméricos y columnas cortas hechas con materiales compuestos) resultando en elementos con rigidez a cortante GAs del mismo orden de magnitud que EI/h2. Los efectos de las fuerzas a cortante son también de gran importancia en el comportamiento estático, de estabilidad y dinámico de soportes elastomericos laminados usados para aislamiento sísmico de edificios. Incrementos significativos en los momentos en los extremos y en las deflexiones son causados por la cortante.
4. AGRADECIMIENTOS
Esta investigación fue llevada a cabo en la Universidad Nacional de Colombia, Facultad de Minas en Medellín. El autor quiere expresar su reconocimiento al Departamento de Ingeniería Civil de la Facultad de Minas y al DIME por el soporte financiero, a Jaime Hernandez-Urrea estudiante de doctorado de la universidad de Illinois en Champaign-Urbana, EE.UU, y Camilo Builes-Mejia estudiante de maestría de la universidad de Nevada en Reno, EE.UU y a Jhon Monsalve-Cano investigador estructural de ACCIONA (Madrid, España) miembros del Grupo de Estabilidad Estructural (GES) de la Universidad Nacional de Colombia por la preparación de las figuras de todos los ejemplos.
REFERENCIAS
[1] ARISTIZABAL-OCHOA, J. DARÍO. Large Deflection and Postbuckling Behavior of Timoshenko Beam-Columns with semirigid connections including Shear and Axial Effects, ELSEVIER Journal of Engineering Structures, Vol. 29 (6), June, pp. 991-1003, 2007. [ Links ]
[2] ROBERTS, T. M., Influence of Shear Deformation on Buckling of Pultruded Fiber Reinforced Plastic Profiles" J. of Composites for Construction, ASCE, Vol. 6(4), Nov. pp. 241-248, 2002. [ Links ]
[3] SALMON, C. G. AND JOHNSON, J.E., Steel Structures: Design and Behavior, 4th Ed., HarperCollins College Publishers (Chapter 14), Michigan , 1996. [ Links ]
[4] TIMOSHENKO, S. AND GERE, J. Theory of Elastic Stability, 2nd Ed., McGraw-Hill, Chapter II, New York , 1961. [ Links ]














