Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.78 n.170 Medellín dez. 2011
REAL ROOTS OF NONLINEAR SYSTEMS OF EQUATIONS THROUGH A METAHEURISTIC ALGORITHM
RAÍCES REALES DE SISTEMAS DE ECUACIONES NO LINEALES MEDIANTE UN ALGORITMO METAHEURÍSTICO
IVÁN AMAYA
B.Sc. Mechatronics Engineering, Ph.D. Engineering student, Universidad Industrial de Santander, iamaya2@gmail.com
JORGE CRUZ
Electronics Engineering student, Universidad Industrial de Santander, mrcrois@hotmail.com
RODRIGO CORREA
Ph.D. on Polymer Science and Engineering, Professor, Escuela de Ingenierías Eléctrica, Electrónica y de Telecomunicaciones, Universidad Industrial de Santander, crcorrea@uis.edu.co
Received for review March 22th, 2011, accepted May 17th, 2011, final version May, 23th, 2011
ABSTRACT: This article describes the use of a numeric strategy to perform a metaheuristic optimization for finding the real roots of a nonlinear equation system. A theorem that shows why it can be treated as an optimization problem is shown. Some two-, three-, and five-equation systems are used as examples of the strategy.
KEYWORDS: nonlinear equations, optimization methods, particle swarm optimization
RESUMEN: Este artículo describe una estrategia numérica de optimización metaheurística, utilizada para determinar las soluciones en el conjunto de los números reales de un sistema de ecuaciones no lineales. Se utiliza un teorema que demuestra la validez de conversión de un problema de solución de ecuaciones no lineales en otro de optimización. A título de demostración, se presentan algunos resultados para sistemas de dos, tres y cinco ecuaciones.
PALABRAS CLAVE: ecuaciones no lineales, métodos de optimización, optimización por enjambre de partículas
1. INTRODUCTION
A nonlinear equations system is defined, explicitly, by (1). It can also be defined in vectorial (or compact) notation by (2). Traditional numerical methods for the solution of these systems are based in algorithms that make use of matricial operations, whose elements belong to the derivatives of its functions. These direct methods pose several variations and approaches, but one of the most used, in engineering, is Newton-Raphson and its variations. Nevertheless, they take a long time to converge, and they only deliver one root (in its traditional form). Therefore, a tendency to migrate to more efficient methods is currently underway. One approach is to transform the solution of the nonlinear system into an optimization problem [1] whose mathematical foundation is included in this article. Most optimization methods, such as Newton's direct root method and its variants, also have an elevated computational cost, which is mainly due to the calculation and storage of the Jacobian (first order derivatives) and Hessian (second order derivatives) matrices that need to be evaluated at each candidate point for every iteration. A first approach proposed to reduce the memory requirements changed the matrices by an approximated one. Methods based on this change are known as quasi-Newton, and the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm is an example of them. It replaces the matrix with an expression that contains several matricial operations (additions, subtractions, products, divisions, and transposes), so the amount of memory required to obtain a new search direction is not vastly reduced [2]. Even so, all of these methods are easily trapped in local minima, or in saddle points, so a starting point near the solution is required, thus limiting its application in real life situations.
A new optimization strategy has appeared, known as metaheuristic algorithms. These make use of stochastic processes, and therefore they are not trapped by the presence of local minima. A method, whose popularity has been on the rise, is particle swarm optimization (PSO), developed in 1995 by Eberhart and Kennedy. It is based on imitating the behavior of animal flocks when looking for new food sources [3], and it is also a cooperative method, where all of its members (or particles) communicate better spots (or optimums) to the swarm [4]. During this research, PSO was used to find the real roots of nonlinear systems, due to its inherent complexity.
This article begins by presenting a mandatory justification, which allows for the transformation of a nonlinear system into an optimization problem. The validation process is performed by using, as an example, systems of two, three, and five equations.
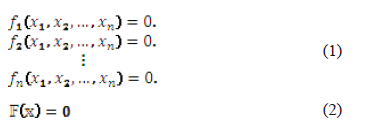
2. FOUNDATIONS
Let equation (1) describe a system of 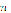 nonlinear equations with
nonlinear equations with 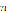 unknowns, where fi is a mapping of the n-dimensional
unknowns, where fi is a mapping of the n-dimensional 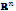 vector
vector 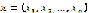 into the real axis
into the real axis 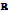 . This is equivalent to considering a function
. This is equivalent to considering a function 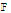 and mapping
and mapping 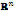 into
into 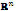 by (3), where each function is a coordinate function of
by (3), where each function is a coordinate function of 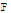 .
.
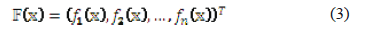
Some required definitions are shown below. They are related to the continuity and differentiability of the functions of  in
in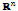 .
.
Definition 1: Let 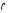 be a function of
be a function of 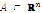 in
in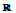 . It is said that
. It is said that 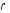 has a limit L in
has a limit L in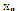 ,
,

if, given any number 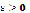 there exists a number
there exists a number 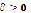 with the property of
with the property of
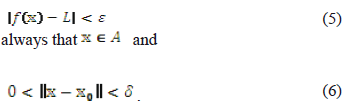
Definition 2: Let 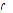 be a function of
be a function of 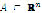 in
in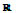 ;
; 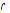 is continuous in
is continuous in 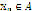 if
if 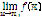 exists and
exists and

Moreover, 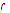 is continuous in
is continuous in 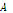 if
if 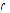 is continuous for every point of
is continuous for every point of 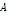 .
.
Definition 3: Let 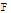 be a function of
be a function of 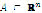 in
in 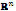 as follows:
as follows:
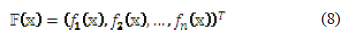
where, fi is mapped from 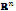 into
into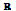 for every i. It is then defined that
for every i. It is then defined that
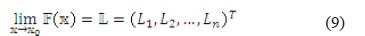
if and only if 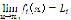 for every
for every 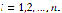
There exist several numerical strategies that strive to solve this type of system, such as the fixed point and multidimensional Newton-Raphson approaches [5]. The first one rarely succeeds, while the other one (more famous in engineering) converges quickly only if the starting point is near the solution, thus reducing its application in real life situations and for bigger problems. Besides, it requires a lot of computer resources and normally finds real roots. However, if initialized with a complex point, it will return a complex solution. The elevated computer requirements are related to the need for calculating, evaluating, and storing the Jacobian matrix and the 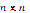 system in all iterations. An improvement to such a disadvantage lies in the quasi-Newton algorithms, such as BFGS, where an approximation matrix is calculated instead of the Jacobian. Even if it lowers the computing requirements, its convergence speed is also reduced to the so called superlinear convergence. Further improvements include a redefinition of the inverse matrix, proposed by Sherman and Morrison [6]. There are also some other options, such as homotopy [7]. Recent literature describes some of the most important methods for solving nonlinear systems [1], [8-11]
system in all iterations. An improvement to such a disadvantage lies in the quasi-Newton algorithms, such as BFGS, where an approximation matrix is calculated instead of the Jacobian. Even if it lowers the computing requirements, its convergence speed is also reduced to the so called superlinear convergence. Further improvements include a redefinition of the inverse matrix, proposed by Sherman and Morrison [6]. There are also some other options, such as homotopy [7]. Recent literature describes some of the most important methods for solving nonlinear systems [1], [8-11]
2.1 An optimization problem
A good approach, whose author cannot be tracked in time, is to transform a problem of solving a system of nonlinear equations into an optimization one [1,5,12-14]. Perhaps one of the most famous examples is the steepest descent method (including its variations), that has been vastly used (even though it only has linear convergence) to obtain the starting points for multidimensional Newton-Raphson [5]. Its main weakness, is the need to calculate the gradient, which can become a very time consuming task and, in some cases, an almost impossible one by analytic means. If done through commercial software, the computational requirements escalate because of the use of symbolic math. The theorem that allows the change into an optimization problem is presented below. It is mentioned for real roots, but its generalization into the complex realm is evident [15].
Theorem 1: Real roots
Let X be a subset of 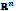 and consider the system (1), where, for each i, fi is a function whose domain contains X, and whose range is within real numbers. Let
and consider the system (1), where, for each i, fi is a function whose domain contains X, and whose range is within real numbers. Let 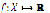 be defined by (10). Note that f needs to be properly defined.
be defined by (10). Note that f needs to be properly defined.
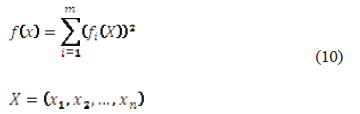
besides:
Proposition 1. Suppose that (1) has solution in 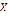 and let
and let 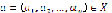 . Therefore,
. Therefore,  satisfies (1) if, and only if,
satisfies (1) if, and only if,  minimizes f.
minimizes f.
Proof. If  satisfies (1), then
satisfies (1), then 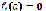 for each
for each 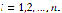 Therefore,
Therefore, 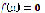 and since
and since 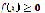 for every
for every 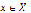 , then
, then  is a minimum for
is a minimum for 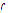 .
.
Now, if  minimizes
minimizes 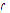 but does not satisfy (1), then
but does not satisfy (1), then 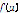 must be a positive number since
must be a positive number since 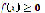 for every
for every 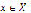 . Given that the system has a solution in
. Given that the system has a solution in 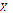 , there exists an
, there exists an 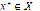 that makes
that makes 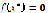
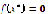 and
and 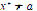 . Therefore,
. Therefore, 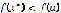 which violates
which violates  being the minimum for
being the minimum for 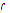 . Note that the general condition on the consistency of the system is vital, since it is always possible to construct
. Note that the general condition on the consistency of the system is vital, since it is always possible to construct 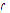 for a given system and, if
for a given system and, if  minimizes it, it does not imply that a solution exists. Therefore, finding the roots for a system of nonlinear equations over a given set
minimizes it, it does not imply that a solution exists. Therefore, finding the roots for a system of nonlinear equations over a given set 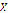 can be transformed into an optimization problem (minimization for this case) of the function
can be transformed into an optimization problem (minimization for this case) of the function 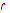 over the set
over the set 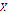 . An algorithm containing this is as follows:
. An algorithm containing this is as follows:
Algorithm 1
Input: The nonlinear equations system (1) and the set 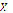
Step 1: Build 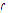
Step 2: Minimize 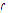 over
over 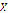 .
.
Step 3: Let 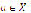 be a minimum for
be a minimum for 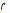 . If
. If 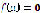 then
then  satisfies (1). Otherwise, it does not have solution in
satisfies (1). Otherwise, it does not have solution in 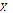 .
.
Based on this theorem, a PSO algorithm was used to generate a real root of the system with a given precision of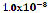 , instead of using it to generate the starting point for Newton's direct root method. Some simulations with systems of two, three, and five nonlinear equations are presented in Section 3. It is important to remark that there is also evidence of other methods for solving nonlinear systems, but due to space restrictions, comparative results are not shown [16].
, instead of using it to generate the starting point for Newton's direct root method. Some simulations with systems of two, three, and five nonlinear equations are presented in Section 3. It is important to remark that there is also evidence of other methods for solving nonlinear systems, but due to space restrictions, comparative results are not shown [16].
2.2 PSO
As mentioned, PSO appeared in 1995, thanks to Eberhart and Kennedy, who studied the social behavior of some animal groups which were looking for new sources of food. Unlike other evolutionary approaches (e.g., genetic algorithms), PSO is cooperative, sharing information with neighboring particles. Neighborhoods may have different topologies, so this is a key point for branches and variations. In its traditional form, the neighborhood is composed of all the particles in the swarm, so every better point found will be communicated to them. Another key point is related to the way its basic equations (position and speed) are updated, traditionally given by (11) and (12), where  ,
,  represent pointers for each position and time step, respectively;
represent pointers for each position and time step, respectively; 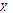 is a particle's position,
is a particle's position, 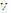 its speed,
its speed, 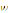 an inertia factor to limit the effect of its previous speed,
an inertia factor to limit the effect of its previous speed, 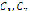 are the self and swarm trust factors,
are the self and swarm trust factors, 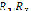 are random numbers (uniformly distributed) between zero and one,
are random numbers (uniformly distributed) between zero and one, 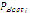 is the best position each particle has found and
is the best position each particle has found and 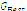 is the best position of all the swarm.
is the best position of all the swarm.
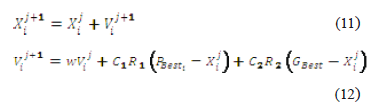
One way to implement this algorithm is:
- Assign a random initial position and zero speed for each particle.
- Evaluate
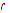 and find
and find 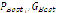 .
. - Update the position and speed for each particle with (11) and (12).
- Evaluate the objective function.
- Compare, for each particle, the evaluated value and
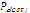 . If it is lower, then update
. If it is lower, then update 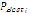 .
. - Select the best particle and compare it to
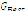 . If lower, then update
. If lower, then update 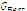 .
. - Compare
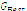 with convergence criteria. If it does not comply, return to 3.
with convergence criteria. If it does not comply, return to 3.
3. EXPERIMENTS AND RESULTS
3.1 Two-equation systems
3.1.1 System (13)
Figure 1 shows the results obtained after executing the PSO algorithm multiple times, starting at (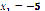 ,
,  ), (
), (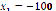 ,
, 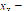 5) and (
5) and (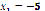 ,
, 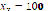 ), respectively. It can be seen that, by increasing the number of particles, the real root found is not critically affected, so, from now on, only total values will be shown for each starting point. This system has two real roots, located at (
), respectively. It can be seen that, by increasing the number of particles, the real root found is not critically affected, so, from now on, only total values will be shown for each starting point. This system has two real roots, located at (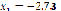 ,
, 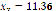 ) and (
) and (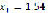 ,
, 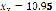 ), that are obtained even if starting at the same point. This behavior is due to the heuristic characteristic of PSO and allows it to avoid getting stuck at a solution.
), that are obtained even if starting at the same point. This behavior is due to the heuristic characteristic of PSO and allows it to avoid getting stuck at a solution.
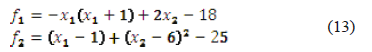
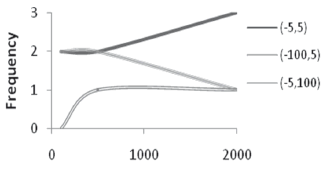
Figure 1. Roots distribution for each swarm size and starting point, system (13)
It is interesting to show that there seems to be a predilection for finding the closest roots, as can be deduced from checking against Figure 2, where in 2/3 of the cases, the solution given by PSO was the closest one. Figure 3 shows how the number of iterations varies with the size of the swarm. As the number of particles rises, it requires fewer cycles to converge. However, this reduction is lower for each increase, so there must be a minimum number of iterations, under which convergence is impossible to achieve (for a given margin of error).
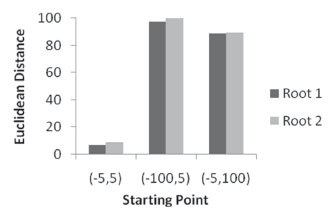
Figure 2. Euclidean distance from each starting point to real roots, system (13)
Figure 3. Iteration variation as a function of the swarm size, system (13)
3.1.2 System (14)
Figure 4 shows the results obtained after implementing PSO for system (14), whose roots are located at (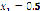 ,
, 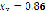 ) and (
) and (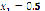 ,
, 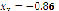 ). Once again, beginning at the same point leads to a different solution. Nevertheless, it is also good to remark that beginning at different points can lead to the same real root.
). Once again, beginning at the same point leads to a different solution. Nevertheless, it is also good to remark that beginning at different points can lead to the same real root.
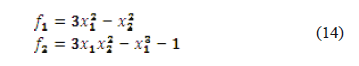
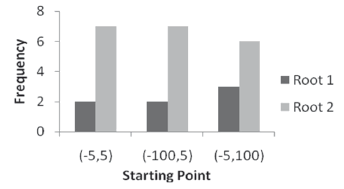
Figure 4. Real roots distribution for system (14)
Figure 5 shows the way computation time behaves as the swarm size increases. Unlike iterations, this variable directly increases with population. This is noteworthy, since one would expect that by having a lower number of iterations (Figure 3), convergence will be achieved faster. However, this could be explained as follows: by having more particles, the computational cost is increased, thus making it so that each iteration takes longer to complete. Figure 5 also shows that only for big swarm sizes (2000 particles), the starting point considerably affects the time required to converge.
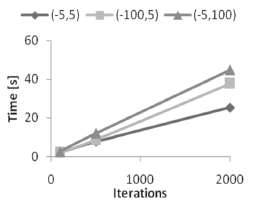
Figure 5. Computation time as a function of the swarm size and the starting point, system (14)
3.1.3 System (15)
Figure 6 shows the results after computing system (15), whose roots are located at (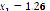 ,
, 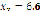 ), (
), (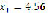 ,
, 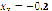 ), (
), (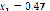 ,
, 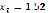 ), and (
), and (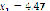 ,
, 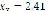 ). When compared to Figure 7, it can be seen that there seems to be a predilection to converge to closer roots. However, this does not mean that it only finds that root, but that it will appear more frequently. Figure 8 once again shows the variation in the number of iterations as the swarm gets bigger. In the same manner as shown previously, the bigger the swarm gets, the less iterations will be required to converge (up to a limit point for a given precision). Moreover, computation time will increase due to the excess of operations.
). When compared to Figure 7, it can be seen that there seems to be a predilection to converge to closer roots. However, this does not mean that it only finds that root, but that it will appear more frequently. Figure 8 once again shows the variation in the number of iterations as the swarm gets bigger. In the same manner as shown previously, the bigger the swarm gets, the less iterations will be required to converge (up to a limit point for a given precision). Moreover, computation time will increase due to the excess of operations.
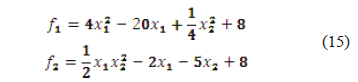
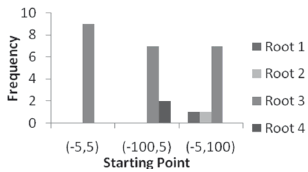
Figure 6. Real roots distribution for system (15)
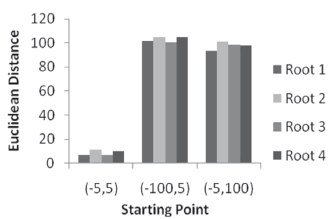
Figure 7. Euclidean distance from each starting point to real roots, system (15)
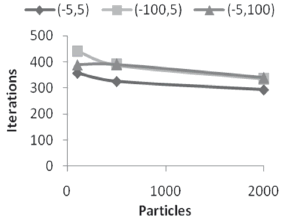
Figure 8. Iteration variation as a function of the swarm size, system (15)
3.1.4 System (16)
Figure 9 presents the results achieved for system (16), whose roots are located at (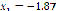 ,
, 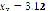 ), (
), (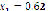 ,
, 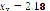 ), (
), (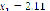 ,
, 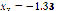 ), and (
), and (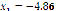
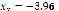 ). It is shown that the starting point does not affect the algorithm's convergence, even though Figure 10 confirms the predilection for closer real roots. Figure 11 shows the behavior of the approximation error as a function of the swarm size. It is easily seen that dependence exists on the number of particles and on the starting point. However, in average terms, an excess of particles will lead to a higher error. Therefore, it is of the utmost importance to choose an appropriate swarm size.
). It is shown that the starting point does not affect the algorithm's convergence, even though Figure 10 confirms the predilection for closer real roots. Figure 11 shows the behavior of the approximation error as a function of the swarm size. It is easily seen that dependence exists on the number of particles and on the starting point. However, in average terms, an excess of particles will lead to a higher error. Therefore, it is of the utmost importance to choose an appropriate swarm size.

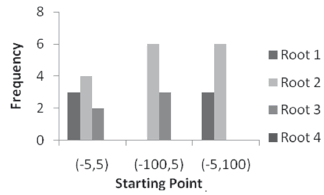
Figure 9. Real roots distribution for system (16)
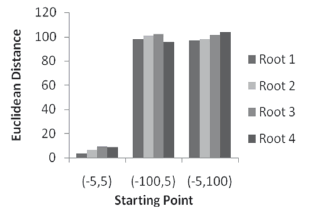
Figure 10. Euclidean distance from each starting point to real roots, system (16)
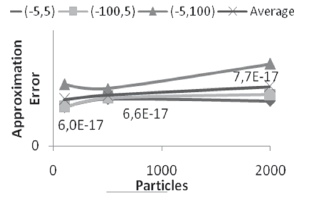
Figure 11. Square error variation as a function of the swarm size, system (16)
3.1.5 System (17)
Figure 12 plots the results after implementing system (17), whose roots are located at (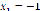 ,
,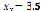 ) and (
) and (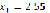 ,
, 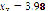 ). Once again, unlike direct search methods, the starting point is not a restriction for the real root found as a solution. Even so, the predilection for closer roots is maintained.
). Once again, unlike direct search methods, the starting point is not a restriction for the real root found as a solution. Even so, the predilection for closer roots is maintained.
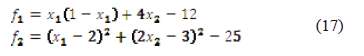
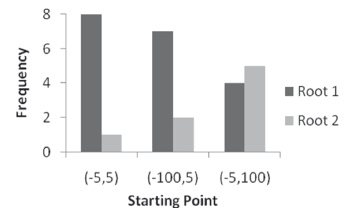
Figure 12. Real roots distribution for system (17)
Figure 13 allows corroboration of the behavior from Figure 5: the bigger the swarm, the lower the number of required iterations. However, computation time will be increased.
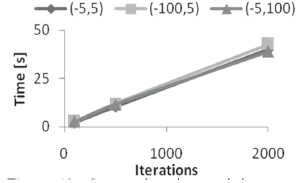
Figure 13. Computation time variation as a function of the swarm size, system (17)
3.2 Three-equation systems
Striving to analyze the combined behavior of systems (18)-(21), some plots are presented with relevant data. Figure 14 shows the variation on the computation time as a function of the number of iterations. It can be seen that it is normal to expect that a smaller system (i.e., one that performs more iterations) takes less time to converge. The relation between swarm size and number of iterations can be checked in Figure 15.
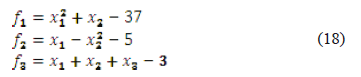
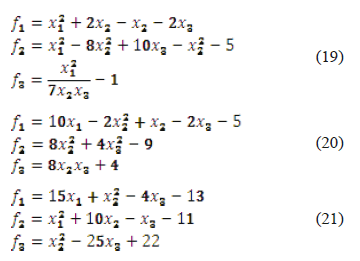
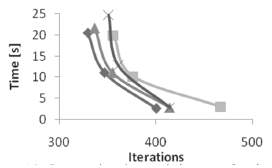
Figure 14. Computation time variation as a function of the swarm size, systems: (18): diamond), (19): square), (20): triangle), and (21): cross)
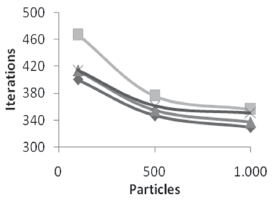
Figure 15. Iteration variation as a function of the swarm size, systems: (18): diamond), (19): square), (20): triangle), and (21): cross)
3.3 Five-equation systems
In an effort to check the behavior of PSO for more complex scenarios, systems (22) and (23) were implemented. Once again, Figure 16 shows that as the number of iterations goes up, the system is simplified and converges in less time.
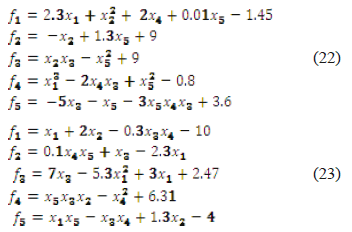
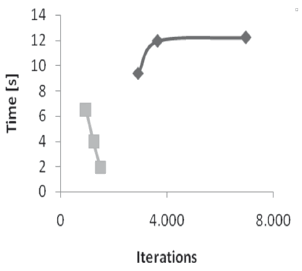
Figure 16. Computation time variation as a function of the swarm size. Systems: (22): diamond) and (23): square).
Figure 17 confirms the fact that smaller systems take more iterations to converge, but they are also simpler and therefore require less time to deliver a solution.
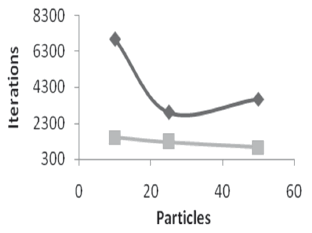
Figure 17. Iteration variation as a function of the swarm size. Systems: (22): diamond) and (23): square).
3.4 Performance Comparison
In an effort to compare the performance (in terms of speed) of PSO against commercial software, plots of average computation time for each type of system were performed. For problems of two and three equations, the average computation time of PSO was well above the one achieved with the commercial software. However, this changes for bigger systems, as can be seen in Figure 18, where it is easily deducted that for 10 particles, the required time is about half of that required by commercial solutions. Therefore, it appears that PSO is a good choice for bigger, more complex systems.
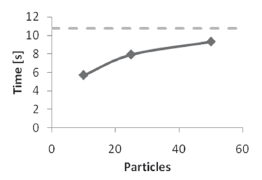
Figure 18. Average computation time for 5 x 5 systems. Diamond: PSO evolution. Dotted line: commercial software time
4. OBSERVATIONS AND CONCLUSIONS
After a careful review of the experimental data, it is natural to conclude that as the swarm gets bigger, the number of required iterations go down (see Figure 3,8,15). Interesting, though, is the fact that it has an adverse effect in the computation time (see Figure 5,13,14). This appears to be contradictory, since if there are less iterations it is expected that it will be quicker. Even though this is true, there is also the fact that by having a bigger swarm, the communication will be performed between more members, so it will adversely affect iteration time. Moreover, there will be more particles that require the calculation of PBest and GBest, so this will also increase the iteration time. In the end, convergence time will be higher than for a smaller swarm. Another interesting effect is the one that the swarm size has on the approximation error, which is directly proportional (see Figure 11). However, at the current time, it remains unknown whether it is due to some type of collision between particles or if it is due to the inertia weight (w), which could be stopping particles before they are able to migrate to a better point. In spite of that, it is of the utmost importance to define a proper swarm size, so that a balance between iterations, computation time and approximation error, is found. If chosen properly, a solution faster than by commercial means can be achieved (Figure 18). It is remarkable that PSO appears to have a preference for finding roots which are closer to the starting point, but still finding the furthest ones.
Finally, and as future research, it would be interesting to study PSO with complex roots and interval mathematics. A first step towards this goal has been taken [17], and we hope to report more conclusive information in the near future.
ACKNOWLEDGMENTS
This work was supported by Vicerrectoría de Investigación y Extensión (Universidad Industrial de Santander), in the framework of project code 5551.
REFERENCES
[1] Grosan, C. and Abraham, A., A New Approach for Solving Nonlinear Equations Systems, IEEE Transactions on Systems, Man, and Cybernetics - Part A: Systems and Humans, Vol. 38, (3), pp. 698-714, May. 2008. [ Links ]
[2] Rao, S. S., Engineering Optimization: Theory and Practice, Fourth Ed. John Wiley & Sons, Inc., pp. 1-829, 2009 [ Links ]
[3] Parsopoulos, K. E. and Vrahatis, M. N., Particle Swarm Optimization and Intelligence: Advances and Applications, First Ed. Information Science Reference, pp. 1-329, 2010. [ Links ]
[4] Clerc, M., Particle swarm optimization, First Ed. ISTE, ,. 243, P. 2006 [ Links ]
[5] Burden, R. L. and Faires, J. D., Análisis Numérico, Sexta Ed. International Thomson Publishing, , pp. 1-802. 1998 [ Links ]
[6] Dennis, J. E. J. and Moré, J. J., Quasi-Newton Methods, Motivation and Theory, SIAM Review, Vol. 19, (1), pp. 46-89, 1997. [ Links ]
[7] Allgower, E. L. and Georg, K., Numerical continuation methods: an introduction, Third Ed. Springer-Verlag New York, Inc., , pp. 1-388. 1990 [ Links ]
[8] Effati, S. and Nazemi, A., A new method for solving a system of the nonlinear equations," Applied Mathematics and Computation, Vol. 168, no. 2, pp. 877-894, Sep. 2005. [ Links ]
[9] Bader, B. W., Tensor-Krylov Methods for Solving Large-Scale Systems of Nonlinear Equations, SIAM Journal on Numerical Analysis, Vol. 43, (3) , 1321 P. 2005. [ Links ]
[10] Salimbahrami, B. and Lohmann, B., Order reduction of large scale second-order systems using Krylov subspace methods, Linear Algebra and its Applications, Vol. 415, (2-3), pp. 385-405, Jun. 2006. [ Links ]
[11] Halton, J. H., Sequential Monte Carlo Techniques for Solving Non-Linear Systems, Monte Carlo Methods and Applications, Vol. 12, (2), pp. 113-141, Apr. 2006. [ Links ]
[12] Ortega, J. M. and Rheinboldt, W. C., Iterative Solution of Nonlinear Equations in Several Variables, First Ed. Academic Press, New York, , pp. 1-599, 1970. [ Links ]
[13] Nie, P., A null space method for solving system of equations, Applied Mathematics and Computation, Vol. 149, no. 1, pp. 215-226, Feb. 2004. [ Links ]
[14] Nie, P., An SQP approach with line search for a system of nonlinear equations, Mathematical and Computer Modelling, Vol. 43, (3-4), pp. 368-373, Feb. 2006. [ Links ]
[15] Gómez, L., Propuesta de demostración del teorema sobre la relación entre sistemas de ecuaciones y el problema de optimización (comunicación interna). pp. 1-2, 2010. [ Links ]
[16] Areiza, M., Un Método Numérico Cerrado para la Solución de Sistemas de Ecuaciones No Lineales en Dos Variables, Dyna, Vol. 69, (137), pp. 45-50, 2002. [ Links ]
[17] Vanegas, D., Barragán, K. S., and Correa, R., Comparación de las técnicas de optimización por análisis de intervalos y la de enjambre de partículas para funciones con restricciones," Ingeniería y Universidad (Universidad Javeriana - Accepted), 2011. [ Links ]














