Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.78 n.170 Medellín dez. 2011
ADVANCED SPATIAL METRICS ANALYSIS IN CELLULAR AUTOMATA LAND USE AND COVER CHANGE MODELING
ANÁLISIS AVANZADA DE MÉTRICAS ESPACIALES EN LA MODELIZACIÓN DE ALTERACIONES EN LA UTILIZACIÓN Y OCUPACIÓN DEL SUELO CON AUTÓMATAS CELULARES
ALEXANDER ZAMYATIN
PhD. Tomsk Polytechnic University, 30 Lenin Avenue, Tomsk, 634050, Russia, zamyatin@tpu.ru
PEDRO CABRAL
PhD. Instituto Superior de Estatística e Gestão de Informação, ISEGI, Universidade Nova de Lisboa, Campus de Campolide, 1070-312 LISBOA, Portugal, pcabral@isegi.unl.pt
Received for review January 21th, 2011, accepted March 29th, 2011, final version April, 1th, 2011
ABSTRACT: This paper proposes an approach for a more effective definition of cellular automata transition rules for landscape change modeling using an advanced spatial metrics analysis. This approach considers a four-stage methodology based on: (i) the search for the appropriate spatial metrics with minimal correlations; (ii) the selection of the appropriate neighborhood size; (iii) the selection of the appropriate technique for spatial metrics application; and (iv) the analysis of the contribution level of each spatial metric for joint use. The case study uses an initial set of 7 spatial metrics of which 4 are selected for modeling. Results show a better model performance when compared to modeling without any spatial metrics or with the initial set of 7 metrics.
KEYWORDS: LUCC modeling, cellular automata, transition rules, spatial metrics, geocomputation, spatial metrics contribution level
RESUMEN: Este artículo expone un abordaje que permite una definición de reglas basadas en la transición de autómatas celulares, para la modelización de alteraciones en la ocupación del suelo, aplicando un análisis avanzada de métricas espaciales. Esta considera una metodología en 4 etapas: i) búsqueda de métricas espaciales adecuadas con correlaciones mínimas; (ii) selección de una vecindad adecuada; (iii) selección de la técnica adecuada para la aplicación de las métricas espaciales; y (iv) análisis del nivel contribución de cada métrica espacial para una utilización conjunta. El caso de estudio incluye un conjunto inicial de 7 métricas espaciales de las cuales son seleccionadas 4 para la modelización. Los resultados muestran un desempeño superior tanto si se compara con una modelización sin métricas espaciales o utilizando las 7 métricas iniciales.
PALABRAS CLAVE: Modelación LUCC, autómata celular, reglas de transición, métricas espaciales, geocomputación, nivel de contribución de las métricas espaciales
1. INTRODUCTION
Land use and cover change (LUCC) modeling is one of the most promising approaches to forecast natural environmental phenomena such as forest fire spread, deforestation, soil erosion, ice and snow cover change, avalanches, etc. [1,2,3]. The LUCC models may be deterministic or stochastic [4]. Due to the stochastic nature of land cover change processes and a significant increase in computer performance, the most promising approach seems to be using stochastic models that consider spatial correlation with cellular automata (CA). A cellular automaton is a collection of cells on a regular grid, with each one having a finite number of states. Each cell evolves through discrete time steps according to transition rules based on the states of the neighboring cells. These transition rules are applied iteratively for a specified number of time steps.
Spatial metrics were developed to provide meaningful ways of measuring landscape characteristics and are usually calculated using a fixed neighborhood. There are over 100 statistical measures of spatial metrics. However, most of them are very similar and have high correlation. These metrics can be calculated with the freely available software FRAGSTATS [5]. Spatial metrics have been widely used in spatial analysis studies or in texture analysis for the classification of remotely sensed images [6,7,8].
The use of different spatial metrics in LUCC modeling has been pursued by many authors. For instance, [9] used the enrichment factor for land use pattern analysis. In [10] a set of spatial metrics for landscape structure investigation was studied. Another example reflecting the use of different sets of spatial metrics can be found in [11].
In this study, we implement LUCC modeling with CA using spatial metrics. We test whether this approach, that increases the number of factors influencing the CA transition rules, makes the LUCC modeling more adequate. The methodology considers: (i) the definition of an adequate neighborhood; (ii) a suitability map that represents the suitability of a cell changing one type of landscape to another (buffer zones, maps of distance to roads and to fresh water sources, etc.); (iii) a comprehensive set of spatial features of the studied landscape measured with selected spatial metrics.
The existence of so many spatial metrics results in the need of solving an individual subtask in CA modeling, i.e., searching for the adequate number of spatial metrics for modeling (ideally 6-7 metrics, because the calculation of each metric in a sliding window can be a computationally intensive task) and searching for the relative importance in the analyzed neighborhood. These spatial metrics should not only be sufficiently different from each other (i.e., have minimal mutual correlation and cover the definition of the different landscape characteristics), but also be efficient when used as a joint set.
The joint use of CA and a set of spatial metrics and characteristics in land cover change modeling are discussed in this paper. The approach includes a preliminary analysis of the spatial characteristics that enables their evaluation and their compatibility for joint use. The analysis is targeted at processing the minimal number of spatial metrics simplifying the calculation process and increasing modeling accuracy.
2. CA MODELING AND TRANSITION RULES
2.1 Typical CA modeling
Cellular automata often use Markov chains to model LUCC and to forecast the thematic map I't for a certain time t in future. The procedure includes a certain number of iterations of a modeling algorithm over thematic maps It2 and It1 for time t2 and t1, a matrix of transition probabilities P = [pij] (stochastic matrix) from the type (class) wi to the type wj, a matrix of the actual number of elements transitions within the time interval [t2;t1], and a matrix of an expected number of element transitions within the time interval [t1;t] assisted by CA rules as set by some fCA. In this case, every CA can be viewed in the form of a matrix MCA = [cij] with order d, where the value of the central element ckh (k = h = (2d+1)/2, here «/» - integer division) in compliance with fCA to a certain extent depends upon the value of all elements of this matrix.
The matrix MCA will be formed by scanning a raster matrix of image It1 = {tmxy = 1,2,…,M; x = 1, 2,…, Cn; y = 1, 2,..., Rn} by a sliding window of a size of (2d + 1) ´ (2d + 1) pixels and by saving the result at the current position {x,y} of the central pixel of a sliding window as a value of pixel c¢kh = fCA(c11, c12,…, ckh,…, cdd) of a new (resulting) image I't (Fig. 1). Here {x,y} is a position of the element ckh in It1, tmxy - a number of Wi landscape type, M - a number of landscape types in the investigated area, Cn - a number of columns, and Rn - a number of rows in a thematic map.
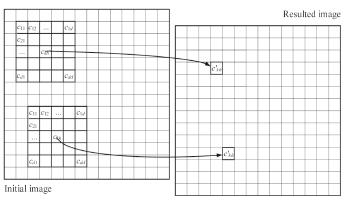
Figure 1. CA operation for collecting new values of resulted image on the basis of initial image
2.2 Definition of transition rules
Considering the aforementioned function fCA for CA, the transition rules in the algorithm of land cover changes modeling should be identified on every point {x,y} of the studied area. These are based on the probability of landscape type substitution from Wi to Wj as pijres~ fCA(pijprob, pijadd, pijsp), where pijprob - probabilistic characteristic, obtained on the basis of a stochastic matrix, pijadd - probability calculated using information from the suitability maps, pijsp - probability, defined by the spatial metrics.
There are different ways of defining the functional dependence fCA and finding probabilities pijprob, pijadd, pijsp. For example, the most logical way to find the joint probability pijres is pijres ~ pijprob × pijadd × pijsp. However, it is obvious that if the value of the probability pijprob, pijadd, pijsp is low, which is very possible in case of their multiplication, then the value pijres will be very small or null. As a result, the transition from type wi to type wj will be not occur in the modeling procedure. To prevent this flaw, we may propose in practice to determine the CA transition rules in every point of the analyzed area based on the resulting transition probability of Wi-th to Wj-th land cover type as (1):
pijres ~ (1 + pijprob) × (1 + pijsp) × (1 + pijadd) - 1 (1)
Following this approach (1), the multiplication of probabilities will not have the previously mentioned inconvenience, and the probabilities pijres will be evenly located in the range [0,1]. It will also simplify the implementation of the modelling algorithm. The probability component pijprob could be obtained as pijprob = pij· ·nj on the basis of a stochastic matrix P = [pij], where nj - number of cells with type wj in a CA neighborhood. The probabilistic component pijadd, i.e., the suitability maps, can be obtained with the help of stochastic maps built with the application of spatial analysis functions available in most GIS software. The probabilistic component pijsp can also be defined by spatial metrics. One possible solution for this nontrivial task is discussed in Section 3.
3. SPATIAL METRICS APPLICATION
The main purpose of a probabilistic component pijsp in CA modeling is accounting for a wide range of possible spatial characteristics of the investigated land cover. This will enable a more accurate identification of possible transition from type Wi to type Wj. It implies the application of spatial characteristics that precede CA modeling of land cover change. The basic concepts of this modeling approach are:the search for a limited number of spatial metrics with low correlation that account for the most important spatial characteristics of the landscape; (2) the evaluation of the size of the analyzed neighborhood in accordance with the applied data; (3) the definition of a method for accounting for the spatial characteristics in computing a probabilistic component pijsp; (4) the analysis of each spatial metric value, the definition of their optimal number, and combination for joint use in CA modeling.
The determined "optimal" finite set of metrics should be used to define a probabilistic component pijsp and then to perform the final CA land cover change modeling on the basis of the expression (1). Let us consider every stage of the proposed methodology in detail:
Search for a set of metrics. At this stage, a finite number of spatial metrics should be selected. Such metrics should first of all, have minimal mutual correlation; secondly, they should cover as far as possible all the relevant spatial characteristics of the landscape. Let us define some spatial characteristic with index l = 1, 2, …, L (L - total number of spatial metrics), calculated for the value tmxyÎIt1 with coordinates {x,y} in a sliding window with a neighborhood order d for a Wk landscape type as Ckl = fc(tmxy, d), x = 1, 2, …, Cn; y = 1, 2, ..., Rn . The calculation of Ckl for all elements of some It1 allows one to form a matrix (defined as Cmkl = {cmxy = Ckl, x = 1, 2,…, Cn; y = 1, 2,..., Rn}). The set of all possible metrics is rather large and will possibly have mutually dependant ones. However, most of the relevant landscape characteristics can be efficiently described using a smaller set by selecting low correlated spatial metrics. The correlation of two random spatial metrics Ckl and Ckl', where l, l' = 1, 2,…, L, in the image It1, can be calculated by Expression (2):
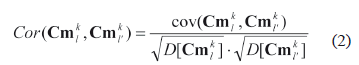
where cov - covariance, and D - variance (dispersion). Having calculated the correlation for L metrics in pairs, we can select for each Ckl such characteristics Ckl' which has the least value Cor(Cmkl, Cmkl') according to (2).
This numerical evaluation allows us to solve the task of searching for a finite set of non-correlated spatial metrics. This selection can be efficiently tested regarding their capacity to reproduce the spatial characteristics of the landscape using visual expert evaluation of the computational results of spatial characteristics for Wk landscape types, where k = 1, 2, …, M.
Search for a neighborhood of an appropriate size. As mentioned before, the key characteristic of any spatial metric is the size (order) of the studied neighborhood. This implies using a set of characteristics defined at the previous stage, where each characteristic can have a different size. However, there are no approaches that allow defining explicitly the most appropriate size of the studied neighborhood for a set of characteristics in CA modeling [12]. CA models are sensitive to scale and neighborhood configuration and, as a rule, the size of the neighborhood is defined by expert evaluation where all the mentioned parameters are considered [13,14,15]. The proposed approach uses all characteristics in different neighborhood sizes and evaluates the impact of all the characteristics on the modeling results.
Defining a method for accounting the spatial characteristics. The spatial characteristics for land cover change modeling with CA could be used in different ways. One of the methods for accounting such characteristics is proposed. Taking into account that there are several characteristics (L), it is reasonable to introduce them into a vector of L length, where the value of the vector components should be specified in the same range for the simplification of processing (e.g., [0;1]). Let us find the vector of "average characteristics" for each Wk landscape type of image
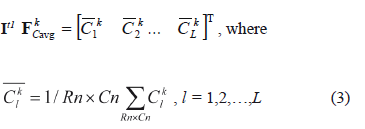
In this case, the value 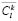 will define some average spatial statistic for Wk landscape type. In the process of modeling and I't image creation, we calculate for every Wk, k = 1, 2, …, M, landscape type a vector of similar characteristics
will define some average spatial statistic for Wk landscape type. In the process of modeling and I't image creation, we calculate for every Wk, k = 1, 2, …, M, landscape type a vector of similar characteristics 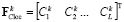 , but only for some current point {x,y} of the image It1 in the neighborhood d. Here, the transition probability from Wi type to Wk type for the point {x,y} could be defined as (4):
, but only for some current point {x,y} of the image It1 in the neighborhood d. Here, the transition probability from Wi type to Wk type for the point {x,y} could be defined as (4):
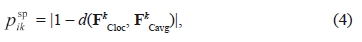
where d (FkCloc, FkCavg) - Euclidean distance between vectors.
Comparing these vectors for every landscape type in pairs, we can define how similar are both spatial characteristics of a Wk type in the current sliding window and the average spatial characteristics on the whole raster image. This allows for the definition of the transition probability for every CA central element of the analyzed neighborhood for every Wi landscape type, and for choosing the highest one for the Wk landscape type.
Analysis of each metrics value in joint use. In practice, it is not easy to define the appropriate set of characteristics because of their correlation, overlapping, and other problems of joint use. To overcome this problem, the authors propose to search for the most effective set of the spatial characteristics which is described below. A series of experiments should be carried out to build a forecast map I't based on It2 and It1 images by means of some unique combinations of spatial characteristics specified for every experiment. Each obtained forecast map I't should be compared to the ground truth map It according to an accuracy criterion. It will allow evaluating the efficiency of the spatial characteristics combination used in every case and also the evaluation of every characteristic in the final modeling result. It should be pointed out that if the ground truth image is absent, it is still possible to evaluate the efficiency of the spatial characteristics used at this stage. In this case, the modeling should be performed in the time period [t2; t1] instead of the period [t1; t]; the image It2 should be considered to be a basic image subject to transformation instead of image It1; and a transition areas matrix should be used as the matrix of expected transition areas. In this case, the result of modeling I't can be compared with the known image It1 and considered a ground truth image, which enables one to evaluate the modeling results and the used set of spatial characteristics. All experiments mentioned above are aimed at selecting a unique combination of characteristics among all possible combinations. For instance, the combination {C1k, 0, 0,…} is used in the first experiment, the combination {C1k, C2k, 0,…}is used in the second experiment, etc., until the very last experiment with the combination {C1k, C2k, …, CLk} that includes all preselected characteristics. As a result of every experiment, we have a forecast map I't. Comparing it with the ground truth map will enable us to obtain the evaluation results according to an accuracy criterion. After that, the results should be arranged in descending order according to an accuracy criterion value. Hence, after ranking each set of characteristics a value of the modeling accuracy is assigned. It allows for evaluating the value and efficiency of every characteristic in the analyzed combinations. The following methodology is recommended for the evaluation of the contribution of every characteristic to the final modeling. It is possible to evaluate a contribution level of a Clk characteristic in a single h-th experiment such as 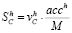 , where h = 1, 2, …, Nexpr, acch - value of accuracy criterion in an h-th experiment, M - the number of characteristics used in modeling, v = {0,1}: v = 0, if Clk is absent in a set of characteristics combination and v = 1 - if Clk is present. The contribution level evaluation of Clk according to the results of N experiments (i.e., integral evaluation) can be defined as (5):
, where h = 1, 2, …, Nexpr, acch - value of accuracy criterion in an h-th experiment, M - the number of characteristics used in modeling, v = {0,1}: v = 0, if Clk is absent in a set of characteristics combination and v = 1 - if Clk is present. The contribution level evaluation of Clk according to the results of N experiments (i.e., integral evaluation) can be defined as (5):

Changing successively the number of experiments N = 1, 2, …, Nexpr, whose overall results define the value of every characteristic for forecast mapping accuracy, we can model the family of curves - contribution level of every characteristic based on Nexpr experiment results. Here, it should be noted that a low number N will conform to "the most successful" combinations of characteristics, that will correspond to the most effective characteristics and ensure the most accurate modeling results. With the increase of N, a contribution level of every characteristic will be approximately the same, converging to the value (6):

4. RESULTS AND DISCUSSION
The proposed methodology of spatial metrics analysis and its application to CA land cover change modeling was implemented in software using C++ Builder IDE. Let us consider in detail an application example and define the appropriate set of spatial metrics and its neighborhood size for the specific land cover change modeling case study.
In the example, the sample time series thematic maps of geoinformation software Idrisi Kilimanjaro - Landuse71.rst (image It2), Landuse85.rst (image It1) and Landuse91.rst (image It) files were used as research data (Clark Labs - IDRISI GIS and Image Processing Software, http://www.clarklabs.org/, Office of Geographic and Environmental Information (MassGIS), Commonwealth of Massachusetts Executive Office of Environmental Affairs, http://www.mass.gov/mgis/). These maps have 9 thematic classes (High Density Residential, Low Density Residential, Industrial/Commercial, Roads/Transportation, Water, Cropland and Pasture, Forest, Wetland, Grass Surfaces) composed of 565 columns and 452 rows. Spatial resolution of the images is 60 m. The spatial pattern of the data used is quite complex which is typical for LUCC data.
From this time data series, the stochastic matrix, matrixes of transition areas, expected transition areas were calculated and the modeling was carried out on the basis of the maps for years 1971 and 1985. The map for year 1991 was used as the ground truth data.
The criteria used to evaluate the accuracy of modeling results were the Receiver/Relative Operating Characteristic (ROC) and Kappa Index of Agreement (KIA). The ROC curve is a graphical plot of the number of true positives versus the number of false positives for a binary classifier system as its discrimination threshold is varied, and it is often used to evaluate the results of a prediction. ROC of 0 means the worst agreement between an obtained map and a ground truth map; ROC of 1 means a complete agreement between an obtained map and a ground truth map. The KIA criterion is mainly used in the field of remote sensing to compare two raster images with a contingency table to find out whether their differences are due to a chance or to a real disagreement or agreement. The KIA of 1 means that two images show a perfect agreement, while the KIA of -1 means that they show a perfect and consistent agreement, and a KIA of 0 means that the two images show a random level of agreement/disagreement (i.e., there is no relationship between them). The application of the proposed methodology is described below.
Stage 1. Selection of a set of spatial metrics. Due to the great number of applicable characteristics and according to expression (1) it is proposed to use an initial set of 7 different spatial characteristics (7)-(13). Spatial characteristics are accounted for each {x,y} element of the raster image It1 in a sliding window with (2d + 1) ´ (2d + 1) elements in a neighborhood for some land cover type Wk, where d can be an order of the neighborhood:
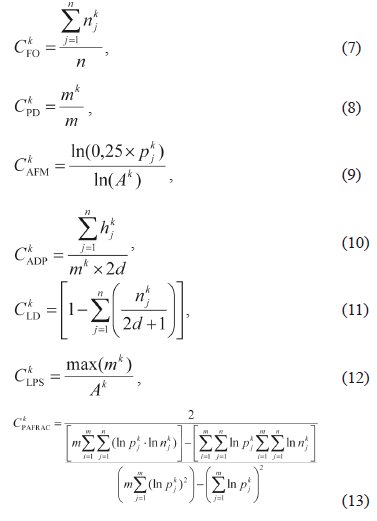
Where n is a number of elements in the neighborhood, m - a number of patches of all types, (a patch is a small area of one type of elements (pixels) of the landscape surrounded by the elements of another landscape type) k index determines the current Wk landscape type, j - index determines a number of a patch), njk - a number of the Wk type elements in the neighborhood, pjk - a patch perimeter, hjk - a number of the elements to the nearest pixel of a Wk type patch, mk - a number of the Wk type patches in the neighborhood, Ak - a total area of the Wk-type patches. For spatial characteristics, the conditional notations descriptions are: CFO - frequency of occurrence (relative frequency of Wk elements occurrence in the neighborhood), CPD - level of patch density (relative frequency of specified patch), CAFM - average fractal measure of perimeters (estimation of average length of patches perimeters), CADP - average distance between patches, CLD - level of division (density of elements), CLPS - level of patch size (patch density), CPAFRAC - perimeter-area fractal dimension (evaluates patch shape complexity). These metrics were calculated for Wk, k = 1, 2, …, M using Idrisi Kilimanjaro raster image (file Landuse85.rst). Then their values were normalized into a range of 0 and 1, and prepared for accounting in psp component calculation.
When a visual assessment is needed, metrics should be presented in the form of probabilistic raster images, where each pixel represents the calculated result for the corresponding characteristic (in this case, in a 5 × 5 elements neighborhood size obtained for Wk "High Density Residential Area" (Fig. 2). The visual analysis of the raster images demonstrates that every characteristic reveals some unique uncorrelated spatial features and delineates the borders between the landscape types. Obviously, characteristics CADP and CLD in comparison with other characteristics revealed few spatial features of the investigated area due to the fact that the corresponding raster images (d and e in Fig. 2) contained minimum information.
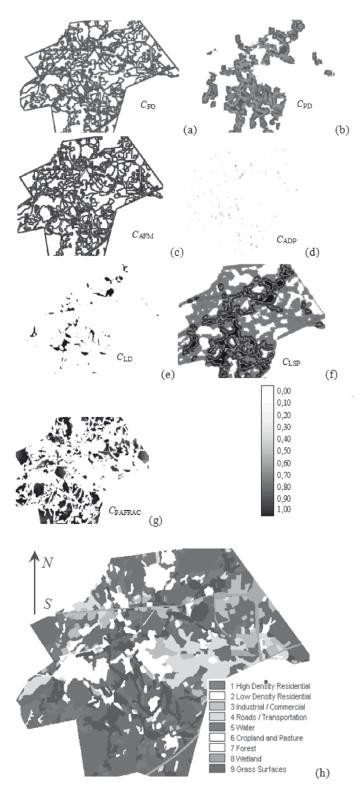
Figure 2. Spatial characteristics for 5 × 5 neighborhood size, obtained for Wk-type "High Density Residential Area" (a-g), initial raster image (h) (maps without scale)
Stage 2. To define the appropriate neighborhood size of spatial characteristics, a set of experiments with 3 × 3, 5 × 5, 7 × 7, 9 × 9, 15 × 15, and 29 × 29 elements in the neighborhood was carried out. The modeling was done with each characteristic from (7)-(13) separately, as well as without any spatial characteristic at all. The experiments allowed for us to prove the appropriateness of the use of spatial characteristics in CA modeling (the accuracy of the modeling results with any characteristic is significantly higher than the same results obtained without accounting for the spatial characteristics), and to find the sensitivity of every single characteristic to its neighborhood size (Fig. 3). Results show that for this type of data (landscape patterns, scale) the best accuracy results in all cases were achieved in the window size with 5 × 5 elements both for KIA and ROC accuracy criteria. It is obvious that the impact of spatial characteristics may significantly depend on both the neighborhood size chosen and the features (e.g., the scale) of specific landscape patterns [12,13,14].
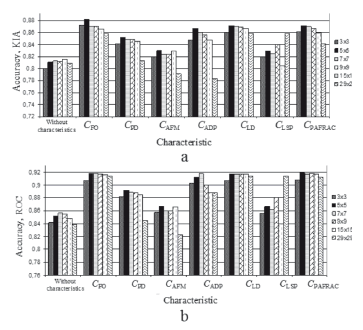
Figure 3. Accuracy of modeling results vs. spatial characteristics in different neighborhood sizes. Accuracy criteria: a) KIA; b) ROC
The numerical and visual evaluation of the results for different neighborhood sizes confirmed that in small neighborhood sizes, like 3 × 3, landscape spatial features are accounted to some extent only. But if we considerably increase the neighborhood size, the generalization level of spatial features becomes too high and spatial features will become hard to distinguish. Hence, to enable easy distinction of landscapes features, it is proposed to use the 5 × 5 neighborhood size for the land cover change modeling.
As an exception, the results obtained with CAFM characteristic (the lowest results in comparison with other characteristics for a neighborhood of any size), and with the CLPS characteristic did not show a robust correlation with a neighborhood size (results of additional experiments for CLPS are depicted in Fig. 4).
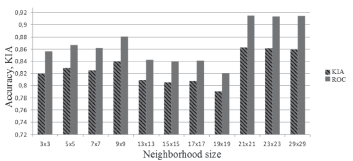
Figure 4. Accuracy of modeling results VS CLPS characteristics used in different neighborhood sizes
Additional research on CLPS application, performed with smaller discrete steps for neighborhood size, proved a significant sensitivity of this characteristic to the scale of the analyzed land type structure. In this case, higher and more robust results of ROC and KIA were obtained for the medium neighborhood size (5 × 5, 9 × 9 elements) and for the large neighborhood size (21 × 21, 23 × 23 and 29 × 29 elements). Considering this behavior, the CAFM and CLPS metrics, were omitted from this case study.
Stage 3. In accordance with the spatial characteristics application, the averaged characteristics can be presented as a vector:
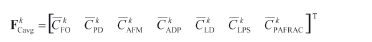
The components of the vector FCavg are calculated for every Wk type of the landscape by moving the sliding window throughout the raster image It1 and calculating the mean value according to (3) of every characteristic from (7)-(13). The local characteristics of every Wk landscape type are calculated in specific location {x,y} using (7)-(13) in the analyzed neighborhood and can be presented as a vector:
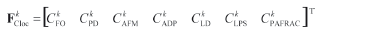
Furthermore, according to the proposed methodology and based on expression (4) a spatial probabilistic component pijsp is defined. This component can be used in expression (1) for the final definition of CA rules for modeling. To escape the impact of padd component in expression (1), we set it to zero for all {x,y}.
Stage 4. This stage is aimed at defining the appropriate set of characteristics in the case of their joint use. The overall number of experiments for 7 characteristics evaluation process is Nexpr = 27 = 128 where all experiments are performed using a unique combination of the characteristics. Every expression resulted in a forecast map. Comparing it with the ground truth map, we may obtain the evaluation results according to the KIA and ROC criteria. After that, the results should be arranged in a descending order according to an accuracy criterion value (in this case, the KIA criterion is chosen, Fig. 5a). In Fig. 5b, the results of the contribution level evaluation for each characteristic obtained where N = 1, 2, …, Nexpr are presented. These were obtained according to the technique for metrics contribution level definition described by Expression (5). Results show that the first experiments have the most accurate results (Fig. 5a, KIA ≥ 0.86, experiments no. 1-30). This means that combinations of spatial characteristics in these experiments are more "useful" for the modeling accuracy than the combinations of characteristics for experiments with the worst accuracy results (Fig. 5a, KIA ≤ 0.86, experiments no. 50-120). The analysis of dependencies (Fig. 5b), shows that the most precise model is obtained using the set of characteristics CFO, CPD, CLPS and CPAFRAC. This demonstrates the highest contribution level of these characteristics in the performed experiments. The smaller significance level of CADP, CLD and CAFM characteristics is proven by the numerical and visual evaluation (Fig. 2d and e and Fig. 3, accordingly).
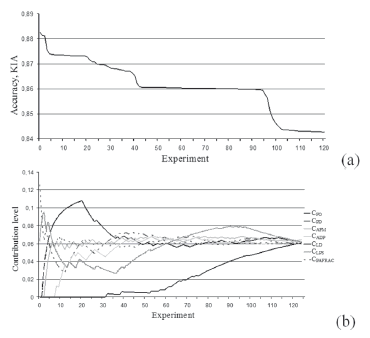
Figure 5. Results of the experiments for different combinations of spatial characteristics ranked in descending order of: a) values of KIA accuracy criterion; b) the contribution level of every characteristic
5. CONCLUSIONS
An approach to advanced spatial metrics analysis for a more effective CA transition rules definition in LUCC modeling has been proposed. This method is based on: (i) the search of the most adequate spatial metrics with a minimal mutual correlation; (ii) the definition of appropriate neighborhood size; (iii) the definition of spatial metrics application; and (iv) the analysis of contribution level of each metric for joint use. A technique for determining the contribution level of the spatial characteristics in different sets throughout CA LUCC modeling has also been proposed. The approach was applied to time series land cover data using a set of 7 spatial characteristics. The analysis of the contribution level and the compatibility of metrics for joint use were carried out. To determine the accuracy of modeling, both ROC and KIA were used. The proposed methodology made possible the evaluation of the value of each characteristic and its compatibility using different combinations for joint use and the reduction of a number of preselected characteristics from 7 to 4 items. This lead to the simplification of the calculation process and to a modeling accuracy higher than the one obtained using any spatial characteristics or with the application of the 7 preselected spatial metrics. Results of the contribution level evaluation for each characteristic showed that the frequency of occurrence (CFO), patch density (CPD), level of patch size (CLPS), and perimeter-area fractal dimension (CPAFRAC) had the highest contribution level according to KIA. The best accuracy results for this type of data (landscape patterns, scale) were found using a neighborhood size of 5 × 5 elements. Due to non-robust results when using different neighborhood sizes, both fractal measure of perimeters (CAFM) and level of patch size (CLPS) are not recommended for use in this case study.
ACKNOWLEDGEMENTS
Research is supported by Russian Foundation for Basic Research (grant no. º11-07-00027-a).
REFERENCES
[1]Benenson, I. and Torrens, P. Geosimulation: Automata-based Modeling of Urban Phenomena, John Wiley & Sons Ltd, Chichester, 2004. [ Links ]
[2] Weng, Q. Land use change analysis in the Zhujiang Delta of China using satellite remote sensing, GIS and stochastic modeling, Journal of Environmental Management, 64, pp. 273-284, 2002. [ Links ]
[3] Cabral, P. and Zamyatin, A. Markov processes in modeling land use and land cover changes in Sintra-Cascais, Portugal, Dyna, 76 (158), pp. 191-198, 2009. [ Links ]
[4] Baker, W., A review of models of landscape change, Landscape Ecology, 2, pp. 111-133, 1989. [ Links ]
[5] Mcgarigal, K., Cushman, S. A., Neel, M. C. and Ene, E Fragstats. Spatial Pattern Analysis Program for Categorical Maps, Computer software program produced by the authors at the University of Massachusetts, Amherst. Available at the following web site: www.umass.edu/landeco/research/fragstats/fragstats.html, 2002. [ Links ]
[6] Cushman, S. A. and. Mcgarigal, K. Patterns in the species-environment relationship depend on both scale and choice of response variables, Oikos, 105, pp. 117-124, 2004. [ Links ]
[7] Cushman, S.A., Mcgarigal, K. and Neel, M., Parsimony in landscape metrics: strength, universality, and consistency, Ecological Indicators, 8, pp. 691-703, 2008. [ Links ]
[8] Mcgarigal, K., Tagil, S. and Cushman, S.A, Surface metrics: An alternative to patch metrics for the quantification of landscape structure, Landscape Ecology, 24, pp. 433-450, 2009. [ Links ]
[9] Verburg, P.H., Nijsc, T., Eck, J., Visser, H. and Jong, K., A method to analyze neighborhood characteristics of land use patterns, Comput. Environ. Urban Syst., 24, pp. 354-369, 2003. [ Links ]
[10] Tischendorf, L., Can landscape indices predict ecological processes consistently? Landscape Ecology, 16, (3), pp. 235-254, 2001. [ Links ]
[11] Li, X. and Yeh, A.G.O., Data mining of cellular automata's transition rules, International Journal of Geographical Information Science, 18, pp. 723-744, 2004. [ Links ]
[12] Benenson, I., Warning! The scale of land-use CA is changing!, Comput. Environ. Urban Syst., 31(2), pp. 107-113, 2007. [ Links ]
[13] Chen, Q. and Mynett, A.E., Effects of cell size and neighbourhood type in a cellular automata based prey predator model, Simulation Modelling Practice and Theory, 11, pp. 609-625, 2003. [ Links ]
[14] Jantz, C.A. and Goetz S.J. Analysis of Scale Dependencies in an Urban Land Use Change Model, International Journal of Geographical Information Science, 19(2), pp. 217-241, 2005. [ Links ]
[15] Kocabas, V. and Dragicevic, S., Assessing cellular automata model behaviour using a sensitivity analysis approach, Comput. Environ. Urban Syst., 30 (6), pp. 921-953, 2006. [ Links ]














