Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.79 n.172 Medellín mar./abr. 2012
SOLUTION OF THE MATHEMATICAL MODEL OF A NONLINEAR DIRECT CURRENT CIRCUIT USING PARTICLE SWARM OPTIMIZATION
SOLUCIÓN DEL MODELO MATEMÁTICO DE UN CIRCUITO ELECTRÓNICO NO LINEAL EN CORRIENTE DIRECTA MEDIANTE OPTIMIZACIÓN POR ENJAMBRE DE PARTÍCULAS
IVÁN AMAYA
Ph.D.(c), Universidad Industrial de Santander, iamaya2@gmail.com
JORGE CRUZ
Universidad Industrial de Santander, mrcrois@hotmail.com
RODRIGO CORREA
Ph.D., Professor ,Universidad Industrial de Santander, crcorrea@uis.edu.co
Received for review June 1th, 2011, accepted February 9th, 2012, final version February, 15th, 2012
ABSTRACT: This article describes a numeric strategy focused on the solution of nonlinear systems of equations, frequently found in the analysis of electronic circuits. This strategy is based on the use of the particle swarm optimization (PSO) algorithm, as an alternative to the traditional Newton-Raphson. First, and as a demonstrative example, a circuit composed of two resistors and a diode were considered. Afterwards, a more complex one comprising one current source, four resistors, and two diodes was implemented. Based on the results, it was observed that the solution alternative is very attractive for solving these kinds of circuits, regardless of their size and complexity.
KEYWORDS: Particle swarm optimization, mathematical model, non-linear electronic circuit, direct current
RESUMEN: El presente artículo describe una estrategia numérica orientada hacia la solución de sistemas de ecuaciones no lineales que con frecuencia aparecen en el análisis de circuitos electrónicos. Esta estrategia se fundamenta en el uso del algoritmo de optimización de enjambre de partículas (PSO), como alternativa al tradicionalNewton-Raphson. Se tomó inicialmente, a título de ejemplo demostrativo, un circuito compuesto de dos resistencias lineales y un diodo. Seguidamente se utiliza otro ligeramente más complejo, constituido por una fuente de corriente, cuatro resistencias y dos diodos. Se encontró que el PSO posee mayor robustez frente al método tradicional. Fundamentado en estos resultados, se observó que esta alternativa de solución tiene características muy atractivas cuando se requiere solucionar este tipo de circuitos independientemente de su tamaño y complejidad.
PALABRAS CLAVE: Optimización mediante enjambre de partículas, modelo matemático, circuito electrónico no lineal, corriente directa.
1. INTRODUCTION
Nonlinear circuits represent a broad range of situations for electronics engineers. Simple, ideal, and linear models can work fine for simple digital electronic circuits, which are composed of integrated circuits (IC). However, the fact of including a common electronic device, such as a diode, takes the scope into the non-linear environment. One approach used to solve this type of system requires the calculation of an operation point under dc sources. In order to reachthis point, several techniques can be used, including Newton-Rapshon's method for solving a system of nonlinear equations. However, its restrictions are well known, including divergences (if the starting point is not chosen well) and excessive amounts of computation time for bigger systems (due to the requirement of storing and evaluating the function and its Jacobian)[1]. In this article, some simulation results using PSO as an optimization strategy to solve the non-linear system of equations are shown.
2. FUNDAMENTALS
2.1. Nonlinear dc circuits
Traditional linear circuits can be modeled (and solved) through strategies such as modal analysis. A nonlinear dc circuit poses a restriction on the solution, forcing one to replace the nonlinear components (such as diodes) by a linearized equivalent circuit. Since this is only valid for a given point (i.e., an operating condition), a second calculation needs to be performed, using the previously achieved information to generate a new solution. This process needs to be continued until a stable solution is obtained. Among the most used strategies, thereare also the analytic, graphical, and numerical ones. The first solution has some advantages, such as global knowledge of the variable behavior, but for most non-linear systems it is almost impossible to achieve. On the other hand, the graphical approach (e.g., the load line method) is good for visualizing the effects of the dc source and the load resistance in the circuit's operating points. However, it has the drawback of being only able to provide approximate values, whose margin of error is associated with the plot's resolution. Numerical techniques, however, offer an approximation method whose error can be user-defined. An approach of this kind that has been traditionally used is the piecewise-linear method, which can be solved analytically or graphically, but whose downside resides in providing multiple solutions that need to be evaluated in order to determine whether they are valid or virtual (i.e., not valid) ones.
Another methodology that has been used in this field is the Newton-Rapshon method (NR) for solving systems of equations, which can be applied to the nonlinear model or to its linearized equivalent [2-6]. Since this approach is an iterative one, the error margin can be defined by the user, therefore adjusting the solution to a desired precision. Baldick [7]qualitatively analyzed the computational effort of three alternatives, which can be used for solving the same example illustrated in this article. They are the NR, chord, and quasi-Newton methods. According to his analysis, the NR method requires relatively few iterations but the computational effort per iteration is high. The chord method requires less effort per iteration, on average, than NR, but the total one may be bigger due to the increased number of iterations required to achieve a desired accuracy. Quasi-Newton methods often have the best overall performance because of the reduced effort per iteration compared to the NR method. Nevertheless, a precise analysis must include the type of functions to be solved and by no means is a general rule.
2.2. Particle swarm optimization (PSO)
PSO was born in 1995 thanks to Eberhart and Kennedy[8], who studied the social behavior of some animal groups when looking for new sources of food. Unlike other evolutionary approaches (e.g.,genetic algorithms), PSO is cooperative, sharing information with neighboring particles [9,10]. Neighborhoods may have different topologies, so this is a key point for branches and variations. In its traditional form, the neighborhood is composed of all the particles in the swarm, so every better point found will be communicated to them. Another key point is related to the way its basic equations (position and speed) are updated, traditionally given by (1) and (2), where , represent pointers for each position and time step, respectively; is a particle's position; its speed; an inertia factor to limit the effect of its previous speed; are the self and swarm trust factors; are random numbers (uniformly distributed) between zero and one; is the best position each particle has found, see (3); and is the best position of the entire swarm, which can be calculated with (4). Since several articles have been published about the use of PSO, and due to space restrictions, a deeper explanation of the method is not provided. However, the interested reader can find useful information in [8,9].
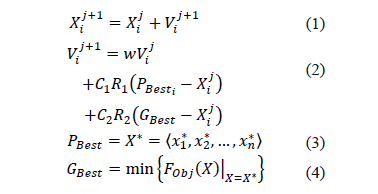
One way to implement this algorithm is:
- Assign a random initial position and zero speed for each particle.
- Evaluate the objective function (user-defined) and find
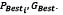
- Update the position and speed for each particle with (1) and(2).
- Evaluate the objective function.
- Compare, for each particle, the evaluated value and
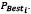 If it is lower, then update
If it is lower, then update 
- Select the best particle and compare it to
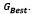 If lower, then update
If lower, then update 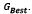
- Compare
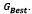 with convergence criteria. If it does not comply, return to 3.
with convergence criteria. If it does not comply, return to 3.
If the solution of a system of equations could be transformed into an optimization problem, metaheuristic approaches would be useful to quickly and accurately find an answer, thus optimizing computer resources. Therefore, this study is carried out in order to analyze how PSO can be useful for solving this electronic engineeringproblem. The following theorem shows how it is possible to transform the solution of the nonlinear equations system into an optimization one [11].
Theorem: Real Roots
LetXbe a subset of 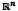 and consider the system (3), where, for each i, fi is a function whose domain contains X, and whose range is within the real numbers. Let
and consider the system (3), where, for each i, fi is a function whose domain contains X, and whose range is within the real numbers. Let 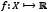 be defined by (3), (note that f is properly defined).
be defined by (3), (note that f is properly defined).
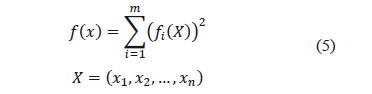
besides:
Proposition 1.Suppose that (3)has solution in 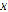 and let
and let 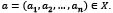 Therefore,
Therefore, 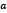 satisfies (3)if, and only if,
satisfies (3)if, and only if, 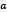 minimizes f.
minimizes f.
Proof. If 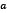 satisfies (3), then
satisfies (3), then 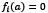 for each
for each 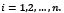 Therefore,
Therefore, 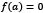 and since
and since 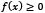 for every
for every 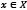 , then
, then 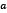 is a minimum for
is a minimum for 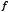 .
.
Now, if 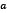 minimizes
minimizes 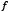 but does not satisfy (3), then
but does not satisfy (3), then 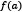 must be a positive number since
must be a positive number since 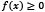 for every
for every 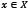 . Given that the system has a solution in
. Given that the system has a solution in 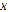 , there exists an
, there exists an 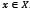 that makes
that makes 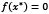 and
and 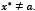 . Therefore,
. Therefore, 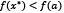 which violates
which violates 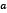 being the minimum for
being the minimum for 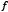 . Note that the general condition on the consistency of the system is vital since it is always possible to construct
. Note that the general condition on the consistency of the system is vital since it is always possible to construct 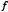 for a given system and, if
for a given system and, if 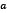 minimizes it, it does not imply that a solution exists. Therefore, finding the roots for a system of nonlinear equations over a given set
minimizes it, it does not imply that a solution exists. Therefore, finding the roots for a system of nonlinear equations over a given set  can be transformed into an optimization problem (minimization for this case) of the function
can be transformed into an optimization problem (minimization for this case) of the function 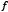 over the set
over the set  . An algorithm containing this is as follows:
. An algorithm containing this is as follows:
Algorithm 1
Input: The nonlinear equations system (3) and the set 
Step 1: Build 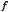
Step 2: Minimize 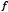 over
over  .
.
Step 3: Let 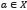 a minimum for
a minimum for 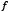 . If
. If 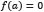 then
then 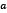 satisfies (3). Otherwise, it does not have solution on
satisfies (3). Otherwise, it does not have solution on  .
.
Based on this theorem, a PSO algorithm was used to generate a real root of the system with a given precision of 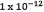 , instead of using it to generate the starting point for Newton's direct root method.
, instead of using it to generate the starting point for Newton's direct root method.
3. EXPERIMENTS AND RESULTS
3.1. Simple Circuit
Figure 1 shows the test circuit for a simple case, where only one nonlinear element is used. This was used as a test, to verify that the algorithm provided correct results. The mathematical model that reflects its behavior is given by (6), where 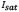 is the saturation current of the diode,
is the saturation current of the diode, 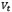 its thermal voltage,
its thermal voltage, 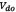 its current operating point, and
its current operating point, and 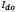 its current. After combining the equations, the objective function shown in (7) is obtained.
its current. After combining the equations, the objective function shown in (7) is obtained.
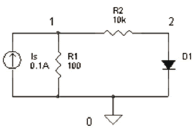
Figure 1. Simple nonlinear dc circuit used for comparing PSO and NR approaches.
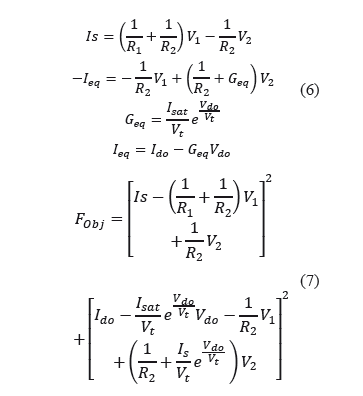
Figure 2 shows the average convergence time for three different starting search spaces. Even though the graphic suggests thatthere is dependence, it can be seen from Figure 3, that this is not true, since it really is an effect of the combination of the averages for each swarm size.
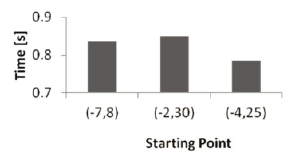
Figure 2. Average convergence time for each initial search space
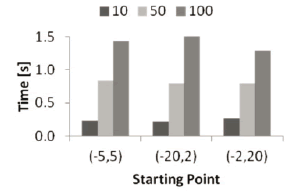
Figure 3. Average convergence time for each initial search space, discriminated by each swarm size
Table 1 shows three test configurations, which were used to determine a parameter sensibility analysis over the PSO method, striving to analyze the way in which the convergence time varied. Figure 4 summarizes the data obtained, showing how PSO behaves under different parameters and amount of particles. It can be seen that especially for big swarms, the effects over 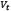 and
and 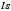 are noticed. Figure 5 shows the variation in convergence time for a point close to the solution and a further one. Once again it is seen that the starting search space does not heavily affect the response time (especially for big swarms).
are noticed. Figure 5 shows the variation in convergence time for a point close to the solution and a further one. Once again it is seen that the starting search space does not heavily affect the response time (especially for big swarms).
Table 1. Test configurations used for parameter sensibility analysis. SI units are assumed
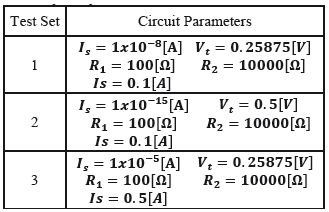
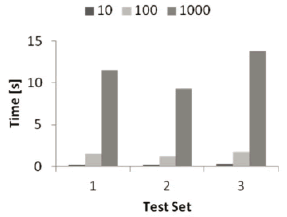
Figure 4. Time variation for each set of parameters and three different swarm sizes
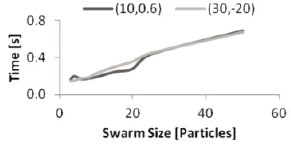
Figure 5. Average convergence time variation as a function of the swarm size, for two different starting search spaces
3.2. More complex circuit
Based on [7], and considering that results are already available, a test circuit was chosen. The non-linear model that reflects its behavior is given by the system of Eq.(8), where each of the variables, as well as the electronic circuit, is shown in Figure 6.
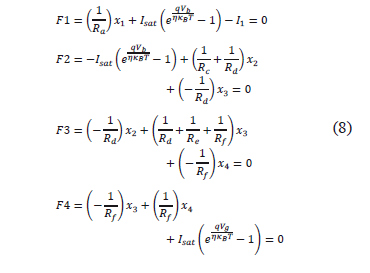
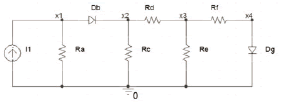
Figure 6. More complex nonlinear dc circuit used for comparing PSO and NR approaches
It is known that
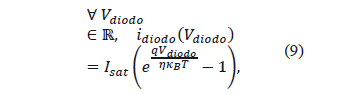
and,
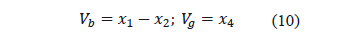
Since the idea is to compare results against validated data, the same constants that Baldick proposed, were chosen[7]:
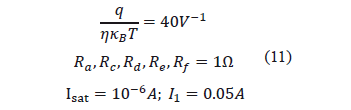
Once again, the equations are combined into a single expression, representing the objective function (12). A computer with the following specifications was used to solve the system:
Manufacturer: TOSHIBA
Model: Satellite A665
Processor: Intel(R) Core(TM) i7 CPU, Q 740 @ 1.73GHz, 1.73GHz
Installed memory (RAM): 6.00GB
OS: Microsoft(R) Windows(TM) 7 Home Premium
System type: 64-bit OS
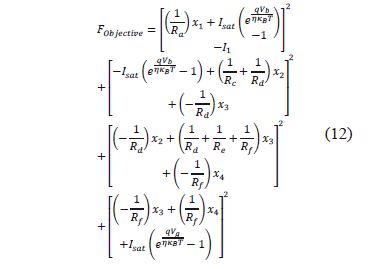
Commercial software (Matlab™), with the Newton-Raphson method, was used to obtain the solution of the test circuit, providing the values of (13).
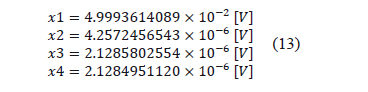
On the other hand, PSO was implemented, with the same commercial software and in the same computer, giving the values shown in (14).
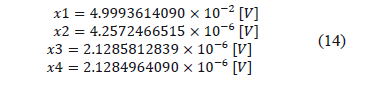
The constants used during the simulations were 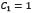 and
and 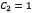 . For 2000 particles, the solution was found in an average time of 98.59 seconds and in 586 iterations. Figure 7 shows the approximation error (i.e., squared function values) for each of the four analysis points. As it can be seen, the error margin was always lower than
. For 2000 particles, the solution was found in an average time of 98.59 seconds and in 586 iterations. Figure 7 shows the approximation error (i.e., squared function values) for each of the four analysis points. As it can be seen, the error margin was always lower than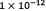 , which was the user defined precision. In a similar fashion, the difference between the results given by the Newton-Raphson approach and the PSO one, were also in this margin, as can be seen in Figure 7.
, which was the user defined precision. In a similar fashion, the difference between the results given by the Newton-Raphson approach and the PSO one, were also in this margin, as can be seen in Figure 7.
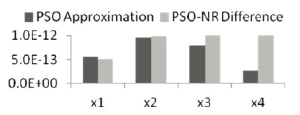
Figure 7. Approximation error for the PSO implementation of the test circuit and difference of 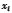 (between the Newton-Raphson and PSO methods)
(between the Newton-Raphson and PSO methods)
Furthermore, more complex tests were performed on the PSO algorithm, checking for variation in convergence time and required number of iterations, mainly. To do so, several runs of the program were executed, varying parameters such as swarm size and starting search space. As can be seen in Figure 8, this does not affect the convergence time (nor the required number of iterations), or at least, not linearly. The previously mentioned figure was obtained as an average of three different swarm sizes (100, 1000, and 2000 particles).In order to dismiss swarm size as a normalizing factor, a plot for each one of them is presented in Figure 9. Once again, it can be easily seen that the data throughout the starting search spaces is quite close, so it does not seriously affect PSO.
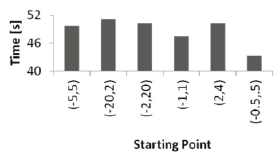
Figure 8. Average convergence time for each initial search space.
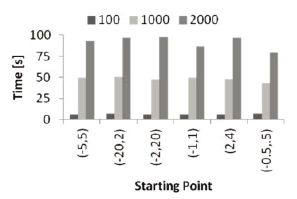
Figure 9. Average convergence time for each initial search space, discriminated by each swarm size
As a next step, the parameters of the nonlinear dc circuit were varied, striving to analyze whether the convergence data (i.e.,time and iterations) are somewhat constant or if they heavily depend on the system. The parameter 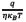 was varied between
was varied between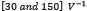 , the resistances were varied in the range
, the resistances were varied in the range 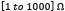 , the source current between
, the source current between 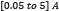 , and the saturation current in the range
, and the saturation current in the range 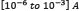 . Figure 10 and Figure 11 show the results obtained for both convergence time and required iterations, but only for some of the combinations. Several things are important to remark upon here. The first one is that for most cases, the computation time goes up(while the number of iterations goes down) as the number of particles is increased. This is interesting because one would expect that by requiring lower iterations, the convergence time will reduce accordingly. However, by using a bigger swarm, the computational effort for calculating and updating each particle's position and speed is increased, thus taking longer to converge. Another important thing to remark here is the result obtained with the test set number four, which achieved its lowest convergence time for a mid-sized swarm. This indicates that there must be an optimum swarm size, which provides the lowest convergence time. However, is likely to heavily depend on the circuit itself, and in its electronic components, so an optimization algorithm should be implemented in future researches.
. Figure 10 and Figure 11 show the results obtained for both convergence time and required iterations, but only for some of the combinations. Several things are important to remark upon here. The first one is that for most cases, the computation time goes up(while the number of iterations goes down) as the number of particles is increased. This is interesting because one would expect that by requiring lower iterations, the convergence time will reduce accordingly. However, by using a bigger swarm, the computational effort for calculating and updating each particle's position and speed is increased, thus taking longer to converge. Another important thing to remark here is the result obtained with the test set number four, which achieved its lowest convergence time for a mid-sized swarm. This indicates that there must be an optimum swarm size, which provides the lowest convergence time. However, is likely to heavily depend on the circuit itself, and in its electronic components, so an optimization algorithm should be implemented in future researches.
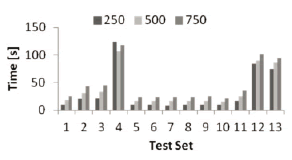
Figure 10. Time variation for each set of parameters and three different swarm sizes
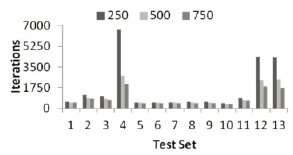
Figure 11. Number of iterations variation for each set of parameters and three different swarm sizes
A third remark is aboutthe rate of increase in the convergence time. It can be seen, from test sets one, three, and four, that increasing the resistances by an order of magnitude does not imply the same increase in the computation time (i.e.,the computation time does not increase linearly with the resistance values). On the other hand, the parameter 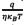 does not seem to have a strong impact on the convergence time (and by extension on the number of required iterations), as can be seen from test sets 5-9. With test sets 11-13, a normal electronics engineering analysis for the circuit, which proposes that
does not seem to have a strong impact on the convergence time (and by extension on the number of required iterations), as can be seen from test sets 5-9. With test sets 11-13, a normal electronics engineering analysis for the circuit, which proposes that 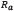 is the most critical element, can be proven. This is obvious, since by varying this element, the current that flows through it will also vary, and therefore the voltage
is the most critical element, can be proven. This is obvious, since by varying this element, the current that flows through it will also vary, and therefore the voltage 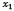 changes, affecting the whole circuit.
changes, affecting the whole circuit.
Striving to find an optimum number of particles for the circuit and to compare PSO performance with Newton-Raphson's method and with commercial software, the test set one was chosen, but the source current was modified to 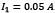 . Figure 12 shows the behavior obtained for different swarms starting at four different search spaces. It can be seen that by taking 4 and 10 particles, the computation time will be minimum for most cases, with the exception that for points closer to the solution, 4 is the best option. Once again, the starting space does not affect the convergence time in a severe way. It is important to note that even if the computation time gets lower for smaller swarms, as soon as its size is below the search dimensions (i.e.,unknowns), the algorithm begins to behave erratically. However, this could be solved by implementing a modification that optimizes in some directions and then in the remaining ones.
. Figure 12 shows the behavior obtained for different swarms starting at four different search spaces. It can be seen that by taking 4 and 10 particles, the computation time will be minimum for most cases, with the exception that for points closer to the solution, 4 is the best option. Once again, the starting space does not affect the convergence time in a severe way. It is important to note that even if the computation time gets lower for smaller swarms, as soon as its size is below the search dimensions (i.e.,unknowns), the algorithm begins to behave erratically. However, this could be solved by implementing a modification that optimizes in some directions and then in the remaining ones.
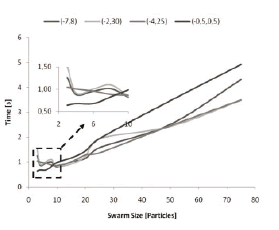
Figure 12. Average convergence time variation as a function of the swarm size, for three different starting search spaces
When compared to NR's times, it was encountered that PSO took longer to converge. However, the data for NR was obtained with starting points quite close to the solution (where NR is known for quickly converging). When started at further points, NR was not able to converge due to problems of singularity in the matrices. Therefore, even if PSO is somewhat slower, it is a technique that allows for solving problems where the optimum point is unknown.
Finally, a summary of the rate of increase on the convergence times for PSO and NR was analyzed. It was found that even if PSO has a higher convergence time, results with NR were only possible if one uses a starting point muchtoo close to the solution. Therefore, for real life situations where the starting point is not known, PSO seems to bea really good choice, so a deeper analysis is underway.
4. CONCLUSIONS
A simple test circuit, comprising one current source, two linear resistors, and a diode, was used as an illustrative example, in order to verify if the algorithm provided the appropriate results, and to see how did the convergence time vary when modifying the circuit's components. Afterwards, a more complex one, comprising one current source, four resistors, and two diodes, was implemented, and a proximity between the results achieved by NR, PSO, and commercial software (Matlab™), was evident. It was found that PSO provides a more robust solution over the traditional NR method, which requires a point quite close to the solution. It was also found that PSO's computation time is not seriously affected by the starting search space, which fortifies it as a viable choice for situations where complete uncertainty of the solution is present. On the other hand, there are two factors that affect PSO's convergence time. The first one is the system parameters, where it was shown that, depending on the circuit, there are some that have a higher impact than the other ones. The second one is that it heavily depends on the swarm size. Therefore, the necessity of implementing an optimization stage, that determines the best number of particles for each problem, is noted, as previously mentioned by[12]. Combined with it, PSO makes a valuable tool for performing dc analysis of more complicated nonlinear circuits.
REFERENCES
[1] Grosan, C. and Abraham, A., A New Approach for Solving Nonlinear Equations Systems, IEEE Transactions on Systems, Man, and Cybernetics - Part A: Systems and Humans, 38, (3) pp. 698-714, May. 2008. [ Links ]
[2] Aprille, T. J. and Trick, T. N., Steady-state analysis of nonlinear circuits with periodic inputs, Proceedings of the IEEE, 60(1), pp. 108-114, 1972. [ Links ]
[3] Nagel, L. and Rohrer, R., Computer analysis of nonlinear circuits, excluding radiation (CANCER), IEEE Journal of Solid-State Circuits, 6(4), pp. 166-182, Aug. 1971. [ Links ]
[4] Chua, L. O., Desoer, C. A. and Kuh, E. S., Linear and nonlinear circuits. McGraw-Hill, New York, 1987. [ Links ]
[5] Rao, S. S., Engineering Optimization: Theory and Practice. John Wiley & Sons, Inc., New Jersey, 2009. [ Links ]
[6] Ortega, J. M. and Rheinboldt, W. C., Iterative Solution of Nonlinear Equations in Several Variables. Academic Press, New York, 1970. [ Links ]
[7] Baldick, R., Applied Optimization Formulation and Algorithms for Engineering Systems. Cambridge University Press, Cambridge, 2006. [ Links ]
[8] Kennedy, J. and Eberhart, R., Particle Swarm Optimization, Proceedings of ICNN95 - International Conference on Neural Networks, Perth, Australia, pp. 1942-1948, 1995. [ Links ]
[9] Clerc, M., Particle Swarm Optimization. ISTE, London, 2006. [ Links ]
[10] Parsopoulos, K. E. and Vrahatis, M. N., Particle Swarm Optimization and Intelligence: Advances and Applications. Information Science Reference, Hershey, 2010. [ Links ]
[11] Amaya, I., Cruz, J., and Correa, R., Real Roots of Nonlinear Systems of Equations Through a Metaheuristic Algorithm, Revista Dyna, 170(78), pp. 15-23, 2011. [ Links ]
[12] Begambre, O. and Correa, R., Validación de un algoritmo híbrido del PSO con el método simplex y de topología de evolución paramétrica, Revista Dyna, 165(78), pp. 255-265, 2011. [ Links ]














