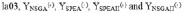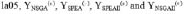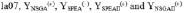Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.79 n.172 Medellín mar./abr. 2012
EVOLUTIONARY MULTI-OBJECTIVE SCHEDULING PROCEDURES IN NON-STANDARDIZED PRODUCTION PROCESSES
PROCEDIMIENTOS DE PROGRAMACIÓN EVOLUTIVA MULTI-OBJETIVO EN PROCESOS PRODUCTIVOS NO ESTANDARIZADOS
MARIANO FRUTOS
Doctor en Ingeniería, Universidad Nacional del Sur y CONICET, Argentina, mfrutos@uns.edu.ar
FERNANDO TOHMÉ
Doctor en Economía, Universidad Nacional del Sur y CONICET, Argentina, ftohme@criba.edu.ar
Received for review December 9th, 2010, accepted January 24th, 2012, final version February, 9th, 2012
ABSTRACT: Scheduling problems can be seen as multi-objective optimization problems (MOPs), involving the simultaneous satisfaction of several goals related to the optimal design, coordination, and management of tasks. The complexity of the goal functions and of the combinatorial methods used to find analytical solutions to them is quite high. The search for solutions (Pareto-optima) is better served by the use of genetic algorithms (GAs). In this paper, we analyze the performance of the non-dominated sorting genetic algorithm II (NSGAII), strength Pareto evolutionary algorithm II (SPEAII), and their predecessors, NSGA and SPEA, when these are devoted to scheduling tasks in non-standardized production activities.
KEYWORDS: Job-shop scheduling, multi-objective optimization, Pareto frontier, memetic algorithm, local search
RESUMEN: En los problemas de programación de la producción que involucran diseñar, coordinar, administrar y controlar todas las operaciones presentes en el proceso productivo, aparecen numerosos problemas de optimización multi-objetivo (MOPs). Los MOPs constan de varias funciones que suelen ser complejas y evaluarlas puede ser muy costoso. La optimización multi-objetivo es la disciplina que trata de encontrar las soluciones, denominadas Pareto óptimas, a este tipo de problemas. La compleja resolución de los MOPs es debida a las dimensiones del problema, al carácter combinatorio de los algoritmos y a la naturaleza de los objetivos los cuales están vinculados a la eficiencia del sistema. En las últimas décadas muchos MOPs vinculados a la producción han sido tratados con éxito con técnicas de resolución basadas en algoritmos genéticos (GAs). En este trabajo se evalúa a NSGAII (Non-dominated Sorting Genetic Algorithm II), SPEAII (Strength Pareto Evolutionary algorithm II) y a sus antecesores, NSGA y SPEA, en el proceso de planificación de la producción no estandarizada.
PALABRAS CLAVE: Programación job-shop, optimización multi-objetivo, frontera de Pareto, algoritmo memético, búsqueda local
1. INTRODUCTION
The scheduling of job-shop (i.e., non-standardized) production activities requires for one to assign in the best possible way the resources used in those processes [1-4]. This, in turn, demands efficient procedures to optimize decisions in those contexts [5,6]. This job-shop scheduling problem (JSSP) has been classified as NP-Hard, meaning that no polynomial algorithm has been found for solving it. Worse yet, the time required to find a solution grows exponentially with the size of the problem [7,8]. Different alternative presentations of the problem have been advanced, in order to accelerate the search for solutions [9-12]. A common feature of most JSSPs is the presence of at least two conflicting goals that have to be simultaneously optimized [13]. Such multi-objective optimization problems usually have many different solutions.
If we assume that, without loss of generality, all the objectives have to be minimized, a multi-objective optimization problem (MOP) requires finding a vector 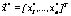 satisfying q inequality constraints
satisfying q inequality constraints 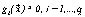 and p equality constraints
and p equality constraints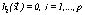 that minimizes
that minimizes 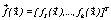 , where the vector of decision variables is
, where the vector of decision variables is 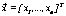 .
.
The class of values that satisfy the constraints defines a region of feasible solutions, denoted 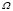 . That is, any
. That is, any 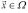 is a possible solution to the MOP. Then,
is a possible solution to the MOP. Then, 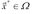 is Pareto optimal if there is no other feasible
is Pareto optimal if there is no other feasible 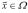 that improves on any goal without worsening another one. Feasible solutions can be partially ordered in terms of Pareto dominance: a vector
that improves on any goal without worsening another one. Feasible solutions can be partially ordered in terms of Pareto dominance: a vector 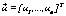 dominates another vector
dominates another vector 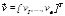 (denoted
(denoted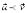 ) if and only if
) if and only if 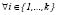 ,
, 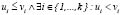 .
.
This allows us to define, for a MOP with objective function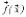 , the optimal Pareto set
, the optimal Pareto set 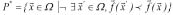 . Finally, this set leads to the definition of the Pareto frontier of the problem:
. Finally, this set leads to the definition of the Pareto frontier of the problem: 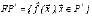 . The main goal in the analysis of MOPs is to find the corresponding Pareto frontier. Since it can contain a large number of points, a good solution consists only of a few points, as close as possible from the exact Pareto frontier and uniformly distributed along its contour.
. The main goal in the analysis of MOPs is to find the corresponding Pareto frontier. Since it can contain a large number of points, a good solution consists only of a few points, as close as possible from the exact Pareto frontier and uniformly distributed along its contour.
Quite useful tools for the search of this approximate Pareto frontier are evolutionary algorithms [14,15]. In particular, genetic algorithms (GAs) are easy to program and implement [16]. Nevertheless, the high rate of convergence of GAs is costly, since this induces the loss of diversity in the solutions, which is reflected in poorly distributed Pareto frontiers. But if a GA is complemented by an efficient local search method, it yields a procedure that solves multi-objective problems requiring a low number of evaluations of the fitness function. This kind of combined algorithm is called a multi-objective memetic algorithm [17].
2. A MULTI-OBJECTIVE MEMETIC ALGORITHM
We introduce the reader here to a multi-objective memetic algorithm that operates on chromosomes representing the sequence of operations to carry out on different machines, one chromosome for each machine. Each chromosome is coded as an ordered list of integers, representing the order in which the jobs will be performed. That is, with values between 0 and n!-1 (n is the total number of jobs to be done), we represent the sequence of jobs in a given machine. For m = 3 (m is the number of machines) and n = 3, 0→123, 1→132, 2→213, 3→231, 4→312 and 5→321. The initial population consists of individuals in which the chromosomes have randomly assigned genes. The algorithm starts by decoding and evaluating these individuals. Two functions are evaluated: makespan (the time required to finish all the jobs) [18] (Eq. 1) and tardiness (the longest delay in finishing a job) [19] (Eq. 2).
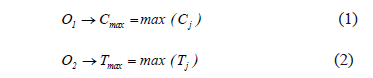
Here Cj is the date in which job j is finished, while Tj is the delay of job j with respect to its intended finishing date. Tj is computed up from Eq. 3, in which dj is the due date of delivery.
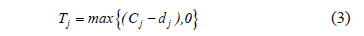
in turn, dj is determined according to Eq. 4, where 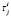 is operation i's processing time for the j job. Here we take b to be 0.20.
is operation i's processing time for the j job. Here we take b to be 0.20.
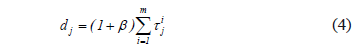
The evaluation determines the criticality of each machine [20]. According to the evaluation, basic genetic operations are applied on the chromosomes. After that, an improvement operator is applied on the individuals, according to the meta-heuristic method known as simulated annealing (SA) [21]. This technique searches locally for better solutions. SA allows for one to search in less favorable areas of the state space, according to the density of potential solutions found. After this step, the resulting individuals are pooled together and subject to non-dominated sorting genetic algorithm II (NSGAII) [22]. NSGAII applies an elitist strategy together with an explicit mechanism to ensure diversity. The elitist procedure consists of choosing the better individuals from the union of the parent and children populations. Fig. 1 describes the operation of the multi-objective memetic algorithm.

Figure 1. Multi-objective memetic algorithm
3. COMPARING NSGAII TO OTHER ALGORITHMS
We consider three multi-objective evolutionary algorithms (MOEAs) and compare them to NSGAII. The MOEAs are: non-dominated sorting genetic algorithm (NSGA) [23], strength Pareto evolutionary algorithm (SPEA) [24], and strength Pareto evolutionary algorithm II (SPEAII) [25].
NSGA classifies individuals by layers of undominated individuals, giving each one in a layer the same value of fitness. This value is proportional to the entire population considered. Once obtained a top layer, it is dismissed and a new layer is considered. The process continues until all the population is classified. Since the individuals in the top layer have the highest degree of fitness, they get more attention than the rest of the population. SPEA creates a file containing the undominated solutions found previously. This file is updated, including new undominated solutions, and deleting the solutions that become dominated. For each one a strength value is computed, proportional to the number of solutions dominated by the individual. The fitness of each member is obtained by computing the strengths of those which dominate it. SPEAII improves over its predecessor by assigning to each possible solution a fitness value that depends both on the number of individuals dominated and the number of those dominating it. It uses also the "closest neighbor" method to assess the density of solutions and guiding the search more efficiently.
4. EXPERIMENTS AND RESULTS
The algorithms discussed above were implemented in a platform and programming language-independent interface for search algorithms (PISA) [26]. PISA is an interface that allows for one to program search algorithms, splitting them in two modules: the variator and the selector. The variator module captures all the specifics of the optimization problem, and its goal is to decode and evaluate the fitness of individuals. The selector module, in turn, is independent of the details of the problem and runs the selection process. Both modules communicate through text files that allow for one to implement the algorithms independently of the underlying programming language and the operations system.
The experiments were run adding a local search stage to each of the aforementioned algorithms. An exploratory analysis showed that the process of improvement of solutions tends to stabilize around the 200th generation. This allowed us to restrict the experiments to stop at the 500th generation, leaving ample room for a late improvement. The experiments were run on a 3.00 GHZ CPU with 1.00 GB RAM. The parameters imposed on the experiments were as follows: the size of the population was 200; the number of generations, 500; the crossover type, uniform; the probability of a crossover, 0.90; the mutation type, two-swap; the probability of mutation, 0.01; the local search type, simulated annealing and; finally, the probability of local search was 0.01. We present the results for problems la01, la02, la03, la04, la05, la06, la07, la08, la09, and la10 [27] in which the goal is to minimize makespan and delay. The procedure is the usual one in these cases [28]. Each algorithm was run 10 times. For each of them, ten classes of undominated solutions were obtained: P1, P2,..., P10. A super-population PT = P1  P2
P2 ...
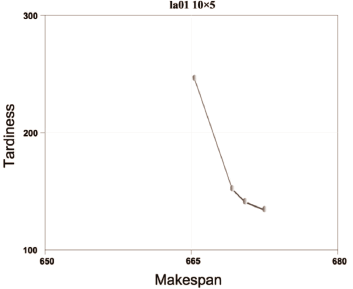
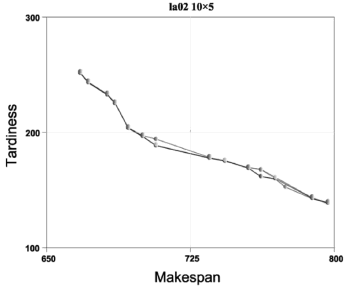
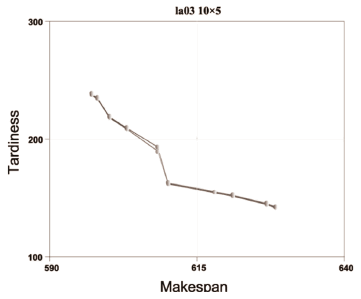
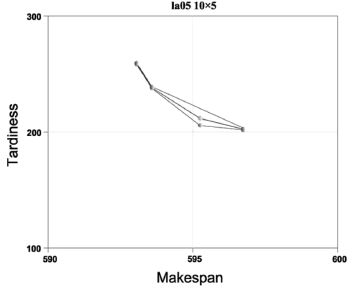
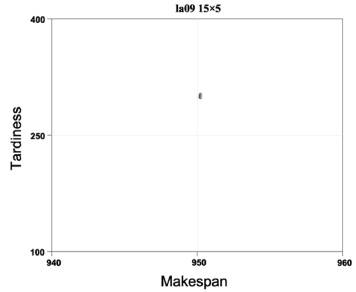
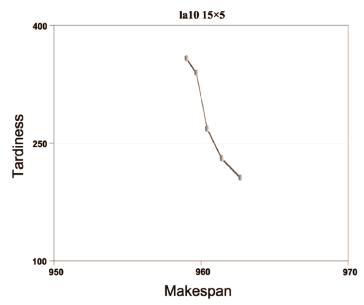
... P10 was created for each algorithm. From each super-population the undominated solutions were extracted to form the Pareto frontiers YNSGA , YSPEA , YSPEAII, and YNSGAII. The outcomes can be seen by observing Figs. 2 to 11.
P10 was created for each algorithm. From each super-population the undominated solutions were extracted to form the Pareto frontiers YNSGA , YSPEA , YSPEAII, and YNSGAII. The outcomes can be seen by observing Figs. 2 to 11.
To approximate the optimal Pareto frontier we take YBK = YNSGA 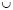 YSPEA
YSPEA 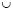 YSPEAII
YSPEAII 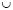 YNSGAII (YBK for best known solutions) and eliminate the dominated solutions. The comparison takes into account which solutions of each algorithm belong to YBK and the solutions from one algorithm dominating the solutions of another: A solution is effective if it belongs to YBK and is not dominated by another one in YBK.
YNSGAII (YBK for best known solutions) and eliminate the dominated solutions. The comparison takes into account which solutions of each algorithm belong to YBK and the solutions from one algorithm dominating the solutions of another: A solution is effective if it belongs to YBK and is not dominated by another one in YBK.
5. COMPARISON PROCEDURE
The algorithms were compared in terms of the resulting values of makespan and delay. For problems la01 (Fig. 2), la04 (Fig. 5), la08 (Fig. 9), la09 (Fig. 10), and la10 (Fig. 11), it can be seen that NSGA, SPEA, NSGAII, and SPEAII have all their solutions in YBK. In these cases, no algorithm improves over the others. For la02 (Fig. 3) 100% of the solutions of NSGAII are in YBK. Even if SPEAII is 100% effective, not all of its solutions are in YBK. SPEA reaches 92.8% of its effectiveness, since from 14 solutions only 1 of them is dominated by an element of YBK. We can see that NSGAII and SPEAII dominate NSGA in 2 solutions and SPEA in 1. Besides, SPEA dominates NSGA in 1 solution. In la03 (Fig. 4), 100% of the solutions of NSGAII are in YBK. Despite the 100% effectiveness of SPEAII, not every alternative of YBK obtains one of its solutions. NSGAII and SPEAII dominate NSGA and SPEA in 1 solution. For la05 (Fig. 6), it can be seen that NSGAII has all its solutions in YBK. Even if NSGA has 100% of effectiveness, not all of its solutions are in YBK. NSGAII dominates SPEA and SPEAII in 1 solution.
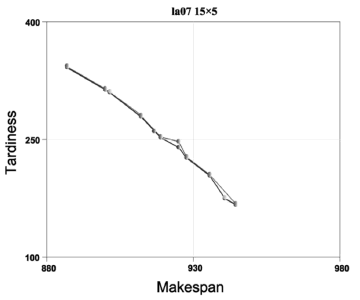
For la06 (Fig. 7), we have that only NSGAII has 100% of its solutions in YBK. NSGAII dominates NSGA, SPEA and SPEAII in 1 solution. In the case of la07 (Fig. 8), we see that all of the solutions of SPEAII belong to YBK. Although NSGAII has 100% effectiveness, not all of its solutions are in YBK. NSGAII and SPEAII dominate NSGA and SPEA in 1 solution. We can see that NSGAII reaches, in most cases, all the solutions in YBK. SPEAII also exhibits a good performance, although not a performance as good as NSGAII. NSGA and SPEA, instead, reach less solutions for YBK. In summary, NSGAII seems to be a better alternative, and justifies its selection as the core GA in our memetic algorithm.
6. CONCLUSIONS
We presented a multi-objective memetic algorithm to solve job-shop scheduling problems (JSSPs) based on NSGAII and simulated annealing. To assess how well this algorithm behaves on this class of NP-hard problems, we run it on a family of well-known JSSPs, arising in non-standardized production contexts. Furthermore, we consider alternative memetic algorithms in which NSGAII is replaced by other multi-objective evolutionary algorithms (MOEAs). In most of the problems, the quality of the solutions found by NSGAII is equal or higher than the results of SPEAII. On the other hand, NSGAII definitely improves over NSGA and SPEA. We can conclude that the multi-objective memetic algorithm here is a good approach for solving JSSPs. Future work involves running this algorithm over other kinds of problems.
ACKNOWLEDGMENTS
This work was funded by two research grants: PIP 112-200801-00804 of the Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET) and PGI 24/J039 of the Universidad Nacional del Sur. We want also thank Dr. Ana C. Olivera for her constant help during this research.
REFERENCES
[1] Adams, J., Balas, E. and Zawack, D., The Shifting Bottleneck Procedure for job-shop scheduling, Management Science, 34 (3), pp. 391-401, 1998. [ Links ]
[2] Park, B. J., Choi, H. R. and Kim, H. S., A Hybrid genetic algorithm for the job-shop scheduling problems, Computers and Industrial Engineering, 45 (4), pp. 597-613, 2003. [ Links ]
[3] Sánchez, F. J., López, J. M., Fernández, J. L. y Páez, F. J., Diseño del interior del habitáculo asistencial de una UVI móvil usando técnicas de optimización basadas en programación lineal, DyNA, 83 (5), pp. 313-320, 2008. [ Links ]
[4] Tsai, C. F. and Lin, F. C., A new hybrid heuristic technique for solving job-shop scheduling problem, Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications, Second IEEE International Workshop, 2003. [ Links ]
[5] Ribas, I., Companys, R. y Mateo, M., Programación bi-criterio para máquinas en paralelo, DYNA, 84 (5), pp. 429-440, 2009. [ Links ]
[6] Chinyao, L. and Yuling, Y., Genetic algorithm-based heuristics for an open shop scheduling problem with setup, processing, and removal times separated, Robotics and Computer-Integrated Manufacturing, 25 (2), pp. 314-322, 2009. [ Links ]
[7] Ullman, J. D., NP-complete scheduling problems. Journal of Computer System Sciences, 10, pp. 384-393, 1975. [ Links ]
[8] Papadimitriou, C. H., Computational complexity, Addison–Wesley, USA, 1994. [ Links ]
[9] Heinonen, J. and Pettersson, F., Hybrid ant colony optimization and visibility studies applied to a job-shop scheduling problem, Applied Mathematics and Computation, 187 (2), pp. 989-998, 2007. [ Links ]
[10] Merkle, D. and Middendorf, M., A new approach to solve permutation scheduling problems with ant colony optimization, Applications of Evolutionary Computing, Proceedings of the EvoWorkshops 2001, 2037, pp. 484-494, 2001. [ Links ]
[11] Wu, C. G., Xing, X. L., Lee, H. P., Zhou, C. G. and Liang, Y. C., Genetic algorithm application on the Job-Shop Scheduling Problem, Machine Learning and Cybernetics, Proceedings of the 2004 International Conference, 4, pp. 2102-2106, 2004. [ Links ]
[12] De Giovanni, L. and Pezzella, F., An improved genetic algorithm for the distributed and flexible Job-Shop scheduling problem, European Journal of Operational Research, 200 (2), pp. 395-408, 2010. [ Links ]
[13] Frutos, M. y Tohmé, F., Desarrollo de un procedimiento genético diseñado para programar la producción en un sistema de manufactura tipo Job-Shop, In Proceedings del VI Congreso Español sobre Meta-heurísticas, Algoritmos Evolutivos y Bioinspirados, Málaga, 2009. [ Links ]
[14] Coello, C. A., Van Veldhuizen, D. A. and Lamont, G. B., Evolutionary algorithms for solving multi-objective problems, Kluwer Academic Publishers, New York, 2002. [ Links ]
[15] Cortés, D., Coello, C. A. and Cortés, N. C., Use of an artificial immune system for Job-Shop Scheduling, In Proceedings of the Second International Conference on Artificial Immune Systems, Edinburgh, Scotland, Springer-Verlag, Lecture Notes in Computer Science, 2787, pp. 1-10, 2003. [ Links ]
[16] Goldberg, D. E., Genetic algorithms in search, optimization and machine learning, Addison–Wesley, Massachusetts, 1989. [ Links ]
[17] Ishibuchi, H., Yoshida, T. and Murata, T., Balance between genetic search and local search in memetic algorithms for Multiobjective Permutation Flow-shop Scheduling, IEEE Transactions on Evolutionary Computation, 7 (2), pp. 204-223, 2003. [ Links ]
[18] Cheng, C. C. and Smith, S. F., Applying constraint satisfaction techniques to job-shop scheduling, Annals of Operations Research, 70, pp. 327-357, 1997. [ Links ]
[19] Armentano, V. A. and Scrich, C. R., Tabu search for minimizing total tardiness in a job-shop, Int. J. Production Economics, 63, pp. 131-140, 2000. [ Links ]
[20] Lin, Y., Pfund, M. and Fowler, J., Heuristics for minimizing regular performance measures in unrelated parallel machine scheduling problems, Computers & Operations Research, 38 (6), pp. 901-916, 2011. [ Links ]
[21] Dowsland, K. A., Simulated annealing, modern heuristic techniques for combinatorial problems, Ed. C R Reeves, Blackwell Scientific Pub, Oxford, 1993. [ Links ]
[22] Deb, K., Pratap, A., Agarwal, S. and Meyarivan, T., A fast and elitist multi-objective genetic algorithm: NSGAII, IEEE Transactions on Evolutionary Computation, 6 (2), pp. 182-197, 2002. [ Links ]
[23] Srinivas, N., Multiobjetive optimization using nondominated sorting in genetic algorithms, Master thesis, Indian Institute of Technology, Kuanpur, India, 1994. [ Links ]
[24] Zitzler, E. and Thiele, L., Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach, IEEE Trans. Evolutionary Computation, 3 (4), pp. 257-271, 1999. [ Links ]
[25] Zitzler, E., Laumanns, M. and Thiele, L., SPEAII: Improving the strength Pareto evolutionary algorithm for multiobjective optimization, In Giannakoglou, Tsahalis, Periaux, Papailiou, and Fogarty (eds), Evolutionary Methods for Design, Optimisations and Control, pp. 19-26, 2002. [ Links ]
[26] Bleuler, S., Laumanns, M., Thiele, L. and Zitzler, E., PISA: A platform and programming language independent interface for search algorithms, In Proceedings of the Evolutionary Multi-Criterion Optimization, 494-508, 2003. [ Links ]
[27] Beasley, J. E., OR-Library: Distributing test problems by electronic mail, Journal of the Operational Research Society, 41 (11), pp. 1069-1072, 1990. [ Links ]
[28] Jaszkiewicz, A., A comparative study of multiple-objective metaheuristics on the bi-objective set covering problem and the Pareto memetic algorithm, Annals of Operations Research, 131 (14), pp. 135-158, 2004. [ Links ]