Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.79 no.176 Medellín Nov./Dec. 2012
STABILITY AND MINIMUM LATERAL BRACING FOR STEPPED COLUMNS WITH SEMI-RIGID CONNECTIONS INCLUDING SHEAR EFFECTS: II) VERIFICATION AND EXAMPLES
ESTABILIDAD Y ARRIOSTRAMIENTO MÍNIMO LATERAL PARA COLUMNAS ESCALONADAS CON CONEXIONES SEMI-RÍGIDAS INCLUYENDO LOS EFECTOS DE CORTANTE: II) VERIFICACIÓN Y EJEMPLOS
J. DARIO ARISTIZABAL-OCHOA
School of Mines, National University, Medellín, Colombia, jdaristi@unal.edu.co
Received for review January 26th, 2012, accepted August 14th, 2012, final version August, 15th, 2012
ABSTRACT: The elastic stability analysis of single-stepped columns with sidesway totally inhibited, partially inhibited, and uninhibited subjected to concentrated axial loads located at the ends and at the intermediate joint including semi-rigid connections and shear force effects are presented using three different approaches in a companion paper. The first two approaches are those by Engesser and Haringx that include the shear component of the applied axial force proportional to the total slope (dy/dx) and to the angle of rotation of the cross section () along the member, respectively. The third approach is a simplified formulation based on the classical Euler theory that includes the effects of shear deformations but neglects the shear component of the applied axial force along the member. Definite criterion on minimum stiffness of lateral bracings for single-stepped columns is also presented. Five comprehensive examples are included that demonstrate the effectiveness of the proposed stability equations and minimum bracing stiffness criteria.
KEY WORDS: bracing, buckling, building codes, columns, construction, computer applications, frames, loads, semi-rigid connections, shear deformations, shoring, stability, stepped columns
RESUMEN: El análisis de estabilidad elástica de columnas con un cambio de sección con derivas laterales totalmente inhibidas, parcialmente inhibidas, y desinhibidas sometidas a cargas axiales concentradas en los extremos y en el nudo intermedio incluyendo los efectos de las conexiones y de las fuerzas a cortante utilizando tres modelos diferentes es presentado y discutido en una publicación adjunta. Los dos primeros modelos son de Engesser y de Haringx que incluyen la componente de la fuerza axial aplicada a cortante proporcional a la pendiente total (dy/dx) y al ángulo de giro de la sección transversal () a lo largo del miembro, respectivamente. El tercer modelo es una formulación simplificada basada en la teoría clásica de Euler, que incluye los efectos de las deformaciones por cortante, pero desprecia la componente a cortante de la fuerza axial aplicada a lo largo de la columna. Se presenta también criterios definidos para determinar la rigidez mínima de los arriostramientos laterales para columnas con un cambio de sección. Se incluye cinco ejemplos completos en esta publicación que muestran la efectividad de las ecuaciones de métodos propuesto en el análisis de estabilidad y en el cálculo de los arriostramientos mínimos para columnas con un cambio de sección.
PALABRAS CLAVE: arriostramiento, pandeo, códigos de construcción, columnas, construcción, aplicaciones informáticas, marcos, cargas, conexiones semi-rígidas, deformaciones por cortante, apuntalamiento, estabilidad, columnas con cambio de sección
1. INTRODUCTION
The elastic stability analysis and the corresponding equations for stepped columns subject to end and intermediate-axial loads including the effects of: 1) lateral and rotational restraints at the intermediate connection and column ends; and 2) shear deformations and shear force along the member caused by the applied axial loads are presented in a companion paper [1]. The main objective of this article is to present the use of the proposed stability equations and to demonstrate their effectiveness.
2. VERIFICATION STUDY AND EXAMPLES
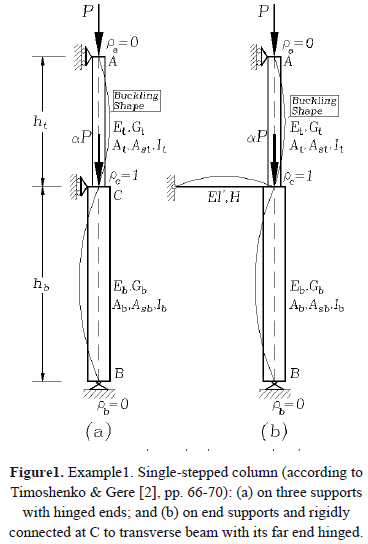
2.1 Example 1. Consider the single-stepped column with hinged ends subjected to concentric axial loads P and aP at A and C shown in Fig. 1a (hinged at A and B: ra = rb = 0; and with rigid connection at C and no exterior rotational restraint: rc = 1, Kc = 0).
Solution: Using Eq. (10) listed in the companion paper and assuming that ra = rb = 0, and kc = 0, the eigenvalue equation becomes
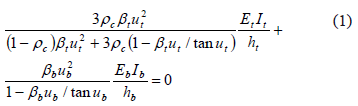
When rc = 1 and Et = Eb, Eq. (1) can be reduced to Eq. (2) as follows:
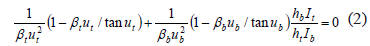
For the particular case of 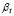 =
=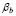 =1 (i.e., neglecting shear effects), Eq. (2) is identical to the solution reported by Timoshenko and Gere [1], Eq. (b), p.67.
=1 (i.e., neglecting shear effects), Eq. (2) is identical to the solution reported by Timoshenko and Gere [1], Eq. (b), p.67.
An additional example was considered assuming that kc = 3EI'/H (bending restraint provided by a transverse beam located at midspan with a hinged far end), ht = hb, It = Ib, bt = bb = 1, Et = Eb = E, and a = 0, as shown in Fig. 1b. Then Eq. (2) becomes
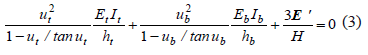
Since ut = ub, Eq. (3) is reduced to Eq. (4)
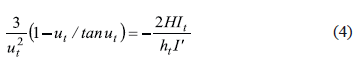
Expression (4) is identical to the solution reported by Timoshenko and Gere ([2], bottom of p. 69). Note that in Timoshenko's notation, ut = 2u1, and ub = 2u2,.
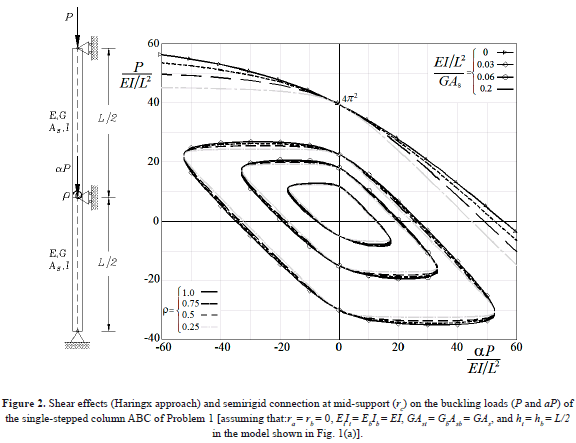
Figure 2 shows the effects of shear deformations (using the Haringx approach) and semi-rigid connection at C (rc) on the buckling loads of the column of Fig. 1(a) assuming that column segments are made of identical material, cross section, and equal length (ht = hb= L/2). Notice that: 1) shear deformations reduce the critical loads P and aP, while the effects of the semi-rigid connection at C are only significant when GAs/(EI/L2) is very large and aP • 0; and 2) the proposed equation is capable of capturing the phenomena of buckling under tension when P or/and aP are negative
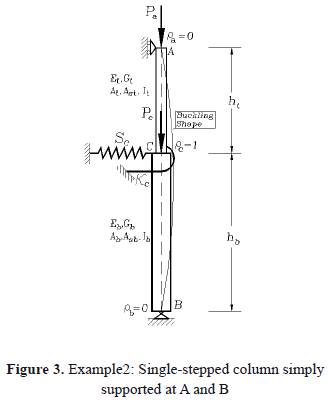
2.2. Example 2. The case under consideration is a single-stepped column with hinged supports at A and B subjected to concentric axial loads Pa and Pc at A and C as shown in Fig. 3 (hinged at A and B and rigidly connected at C: ra = rb = 0, and rc = 1).
Using Eq. (10) listed in the companion paper and assuming that ra = rb = 0 and rc = 1, the eigenvalue equation becomes
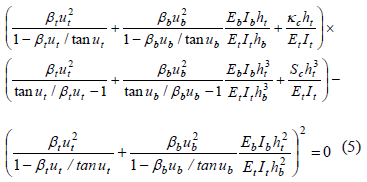
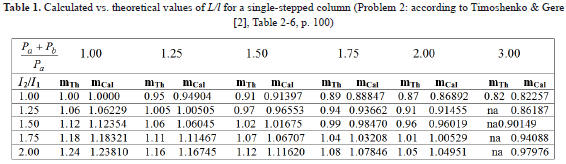
Results from Eq. (5) were tested against tabulated values presented by Timoshenko and Gere ([2], Table 2-6, p. 100) for the particular case of Sc = kc = 0, bt = bb = 1 and Et = Eb = E. The values of the reduced length L of the column calculated from Eq. (5) which are listed in Table 1 (denoted as mCal) are practically identical to those derived by Timoshenko and Gere [2] denoted as mTh) where (Pa+Pc)cr = p2EI/L2.
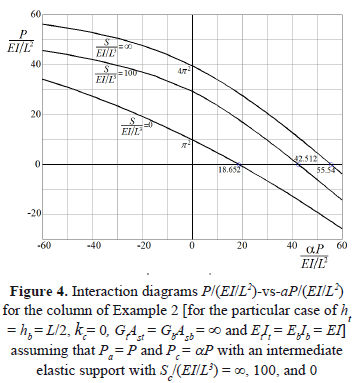
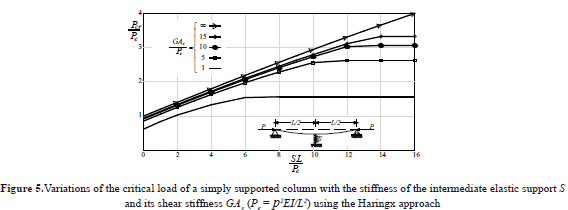
Figure 4 show a series of interaction diagrams of P/(EI/L2)-vs-aP/(EI/L2) for different values of S/(EI/L3) all obtained using Eq. (5) for the particular case of ht = hb = L/2, GtAst = GbAsb = ∞ and EtIt = EbIb = EI. Figure5 shows the variations of the compressive buckling load Pcr of a simply supported beam with the stiffness of the intermediate elastic support S located at midspan for different values of GAs/Pe (notice that Pcr and S are normalized with respect to Pe = p2EI/L2).
Notice also that: 1) the values indicated in Fig. 5 corresponding to the curve with S = 0 are identical to those presented by Timoshenko and Gere ([2], p. 100 Table 2-6 for n = 1); 2) the buckling load capacity of the beam-column is affected significantly not only by the location and stiffness of the mid-support but also by the magnitude of the shear stiffness of the members as shown by the curves in Fig. 5 and 3) the curve corresponding to GAs/Pe = ∞ in Fig. 5 shows that the compressive critical load increases in approximately the same proportion as S. This curve is identical to that presented by Timoshenko and Gere ([2], p. 73).
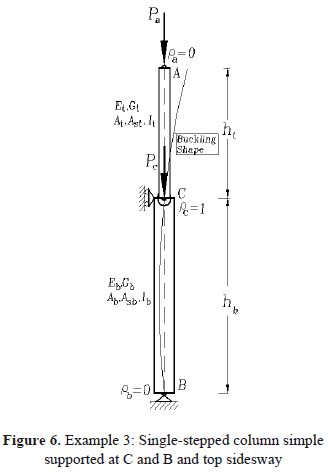
2.3 Example 3. The validity of Eq. (12) was tested against the solutions obtained utilizing the classical method of slope-deflection (Salmon and Johnson [3], p. 840) for a stepped column with hinged ends subjected to concentric axial loads Pa and Pc at A and C as shown in Fig. 6 (free at A: ra = 0, Sa = 0; braced at C with no exterior rotational restraint: rc = 1, Kc = 0; and hinged at B: rb = 0).
Substituting into Eq. (12) ra = rb = 0, rc = 1, and Kc = 0, the eigenvalue equation becomes
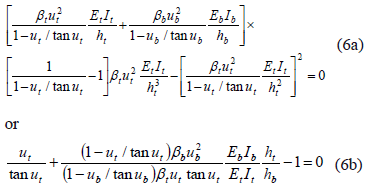
For the particular case: Pc = 0, ht = hb = h, EtIt = EbIb = EI, andbt = bb = 1, the stability equation is reduced to 2ut = tanut, whose solution is ut = 1.16556 or (Pa)cr = p2EI/(2.6953h2). Using the slope-deflection method (Salmon and Johnson [3], pp. 840-842) a stability equation identical to (6b) can be obtained.
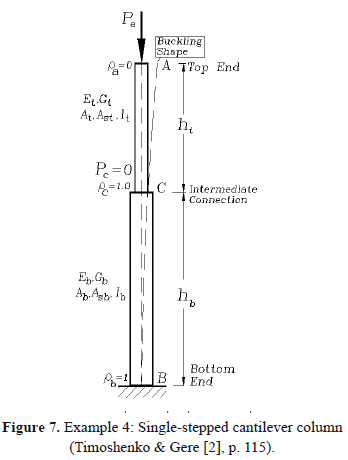
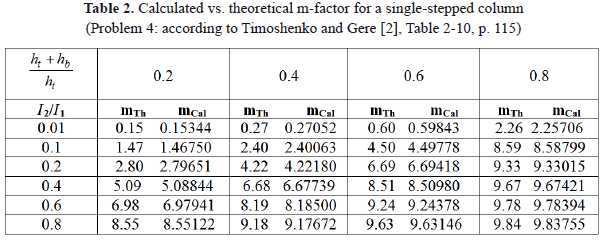
2.4 Example 4. Results from Eq. (13) were tested against tabulated solutions presented by Timoshenko and Gere ([2], Table 2-10, p. 115) for a stepped cantilever Euler-Bernoulli column (bt = bb = 1) shown in Fig. 7 free at A (ra = Sa = 0), rigidly connected and unrestrained at C (rc = 1, Sc = Kc = 0), and perfectly fixed at B (rb = 1).
Table 2 shows that the values of m calculated using Eq. (13), which are listed with five significant figures, are practically identical to those by Timoshenko. Note that m is for the hinged-hinged column, and m/4 for the cantilever column, where m is used by Timoshenko in Pcr = mEI2/(h1+h2)2.
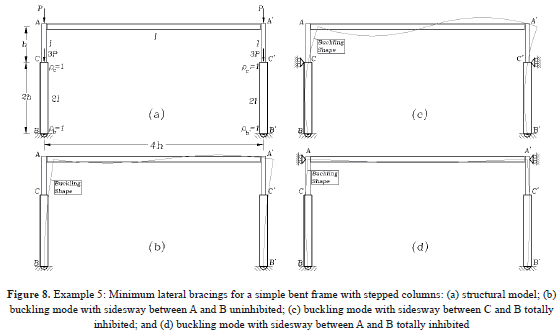
2.5 Example 5: Minimum lateral bracing for a bent-up frame
Utilizing the minimum bracing criteria and the steps described in the companion paper, determine the lateral bracings required to convert the bent frame shown in Fig. 8a into a braced frame. The bracings that need to be analyzed are: 1) Sa along the top level (i.e., frame braced at A and A' only); 2) Sc at the intermediate joint (i.e., frame braced at C and C' only); and 3) Sa and Sc along the top and intermediate joints (i.e., frame braced at A and C). Assume that rb = rc = 1 in both columns and neglect the effects of shear deformations (i.e., b = 1 in all members).
Solution: Since the frame is symmetrical, columns AB and A'B' are both identical with the same loads and boundary conditions. Therefore, the stability analysis can be reduced to that of a single column.
The first step is to find the fixity factors at the column ends for unbraced and braced conditions. Relationships between the rotational restraints and the fixity factors in framed structures are presented in the Appendix of the companion paper. For this particular frame, the fixity factors are as follows:
i) For unbraced conditions along AA', the frame would buckle in a anti-symmetric shape (Figs. 8b-c) with the beam providing rotational restraints at both ends A and A' of magnitude 6EI/L = 1.5EI/h (since L = 4h). Therefore, ra = 1/(1+3/1.5) = 1/3, and rb = rc = 1.
ii) For braced conditions along AA', the frame would buckle in a symmetric shape (Fig. 8d) with the beam providing rotational restraints at both ends A and A' of magnitude 2EI/L = 0.5EI/h. Therefore, ra = 1/(1+3/0.5) = 1/7, and rb = rc = 1.
The required bracings for column AB for each one of the requested cases are calculated as follows:
- Braced at top end A only. Taking into consideration that: It = I, ht = h, Ib = 2I, ht = 2h, Pa = P, Pc = 3P, ra = 1/3, and rb = rc = 1, the solution for braced conditions obtained from Eq. (11) are: (Pa)cr = 0.19072(p2EI/h2) and (Pa+Pc)cr = 0.76288(p2EI/h2) (or ut = p
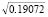 = 1.37198 and ub = p
= 1.37198 and ub = p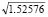 = 3.88055). Now, the magnitude of Sa can obtained directly from Eq. (11) by substituting the values of ut = 1.37198 and ub = 3.88055, ra = 1/3, and rb = rc = 1. The result is Sa = 3.3818EI/h3 per column.
= 3.88055). Now, the magnitude of Sa can obtained directly from Eq. (11) by substituting the values of ut = 1.37198 and ub = 3.88055, ra = 1/3, and rb = rc = 1. The result is Sa = 3.3818EI/h3 per column. - Braced at the intermediate joint C only. Taking into consideration that: It = I, ht = h, Ib = 2I, ht = 2h, Pa = P, Pc = 3P, ra = 1/3, and rb = rc = 1, the solution for braced conditions obtained from Eq. (12) are: (Pa)cr = 0.20909(p2EI/h2) and (Pa+Pc)cr = 0.83637(p2EI/h2) (or ut = p
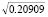 = 1.43654 and ub = p
= 1.43654 and ub = p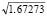 = 4.06315). Now, the magnitude of Sc can obtained directly from Eq. (12) by substituting the values of ut = 1.43654, ub = 4.06315, ra = 1/3, and rb = rc = 1. The result is Sc = 2.77322EI/h3 per column.
= 4.06315). Now, the magnitude of Sc can obtained directly from Eq. (12) by substituting the values of ut = 1.43654, ub = 4.06315, ra = 1/3, and rb = rc = 1. The result is Sc = 2.77322EI/h3 per column. - Braced at end A and at the intermediate joint C simultaneously. Taking into consideration that: It = I, ht = h, Ib = 2I, ht = 2h, Pa = P, Pc = 3P, ra = 1/7, and rb =rc = 1, the solution for braced conditions obtained from Eq. (10) are: (Pa)cr = 0.329338(p2EI/h2) and (Pa+Pc)cr = 1.31735(p2EI/h2) (or ut = p
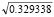 = 1.802898 and ub = p
= 1.802898 and ub = p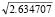 = 5.09936).
= 5.09936).
Now, the magnitude of Sa can obtained directly from the characteristic equation 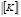 = 0 by deleting the second row and column (or
= 0 by deleting the second row and column (or 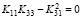 ) and substituting the values of ut = 1.802898, ub = 5.09936, ra= 1/7, and rb =rc = 1. The result is Sa = 47.3354EI/h3 per column.
) and substituting the values of ut = 1.802898, ub = 5.09936, ra= 1/7, and rb =rc = 1. The result is Sa = 47.3354EI/h3 per column.
Similarly, Sc can obtained directly from the characteristic equation 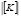 = 0 by deleting the third row and column (or ) and substituting the values of ut = 1.802898, ub = 5.09936, ra = 1/7, and rb = rc = 1. The result is Sc = 1.096677EI/h3 per column.
= 0 by deleting the third row and column (or ) and substituting the values of ut = 1.802898, ub = 5.09936, ra = 1/7, and rb = rc = 1. The result is Sc = 1.096677EI/h3 per column.
It is interesting to note that: 1) the trend for this particular frame is indicated by Eq. (18) as follows: (Pa+Pc)cr = 1.31735(p2EI/h2) > 0.83637(p2EI/h2) > 0.76288(p2EI/h2) > 0.16074(p2EI/h2) (this last value corresponds to the unbraced frame); and 2) the required lateral bracing at A is relatively small compared to that required at the intermediate joint C.
3. SUMMARY AND CONCLUSIONS
A complete column classification and the corresponding stability equations for single-stepped columns with sidesway totally inhibited, partially inhibited, and uninhibited subjected to concentrated axial loads located at the ends and at the intermediate joint including the shear force effects are presented using three different approaches in a companion paper.
To understand the four-way classification of single-stepped columns and post shores, the corresponding stability equations, five examples are used in this paper and the results are compared to those using other methods. A verification study indicates that the calculated elastic buckling loads are theoretically exact.
Analytical studies indicate that: 1) the stability of a single-stepped column increases substantially with the magnitude of the lateral restraints and the fixity at the base and at the intermediate connection; 2) shear deformations and the shear forces induced by the applied axial loads reduce the buckling loads; 3) the degree of fixity at the top end has less influence on the overall stability of stepped columns and post shores in frames with sidesway inhibited than in frames with sidesway uninhibited; 4) the critical axial loads using the Engesser approach is lower than that using the Haringx and simplified Euler approaches; 5) the critical loads in tension and in compression predicted by the Haringx approach are very sensitive to the shear stiffness GAs; 6) the Haringx approach is the only one among the three approaches capable of capturing the phenomena of tension buckling; and 7)as expected, the critical axial loads in compression are highly affected by the degree of flexural fixity at the supports, but the critical axial loads in tension are not affected as much. It is important to emphasize that shear effects are not of significance and can be neglected for slender columns of solid cross sections like rectangular and I-cross sections.
ACKNOWLEDGMENTS
The research presented in this paper was carried out at the National University of Colombia at Medellin. The author wants to express his appreciation to Jaime Hernandez-Urrea, currently a Ph.D. student at the University of Illinois at Champaign-Urbana and former member of the Structural Stability Group GES of the National University of Colombia at Medellin for helping and preparing the figures of all the examples.
NOTATION

REFERENCES
[1] Aristizabal, J. D., Stability and minimum lateral bracing for stepped columns with semi-rigid connections including shear effects: I) Theory, Revista DYNA, 174, 2012, pp. 96-106. [ Links ]
[2] Timoshenko, S. P., and Gere, J. M., Theory of Elastic Stability, 2nd Ed., McGraw-Hill Book Inc., New York, N.Y. 1961. [ Links ]
[3] Salmon, C. G. and Johnson, J.E., Steel Structures: Design and Behavior, 4th Ed., HarperCollins College Publishers (Chapter 14), 1996. [ Links ]