Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.79 no.176 Medellín nov./dez. 2012
WEIGHTED TIME SERIES ANALYSIS FOR ELECTROENCEPHALOGRAPHIC SOURCE LOCALIZATION
ANÁLISIS DE SERIES DE TIEMPO PONDERADAS PARA LA LOCALIZACIÓN DE FUENTES ELECTROENCEFALOGRÁFICAS
EDUARDO GIRALDO
Msc. Professor. Programa de Ingeniería Eléctrica, Universidad Tecnológica de Pereira, egiraldos@utp.edu.co
DIEGO PELUFFO-ORDOÑEZ
Msc. Facultad de Ingeniería y Arquitectura, Universidad Nacional de Colombia sede Manizales, egiraldos@utp.edu.co
GERMÁN CASTELLANOS-DOMÍNGUEZ
PhD. Professor. Facultad de Ingeniería y Arquitectura, Universidad Nacional de Colombia sede Manizales, cgcastellanosd@unal.edu.co
Received for review March 9th, 2012, accepted June 29th, 2012, final version August, 2th, 2012
ABSTRACT: This paper presents a new method to estimate neural activity from electroencephalographic signals using a weighted time series analysis. The method considers a physiologically based linear model that takes both spatial and temporal dynamics into account and a weighting stage to modify the assumptions of the model from observations. The calculated weighting matrix is included in the cost function used to solve the dynamic inverse problem, and therefore in the Kalman filter formulation. In this way, a weighted Kalman filtering approach is proposed including a preponderance matrix. The filter's performance (in terms of localization error) is analyzed for several SNRs. The optimal performance is achieved using the linear model with a weighting matrix computed by an inner product method.
KEYWORDS: inverse problem, brain mapping, weighting matrix.
RESUMEN: Este artículo presenta un nuevo método para la estimación de actividad neuronal a partir de señales electroencefalográficas usando análisis de series de tiempo ponderadas. El método considera un modelo lineal basado en restricciones fisiológicas que tiene en cuenta tanto la dinámica espacial como la temporal, y una etapa de ponderación que modifica las suposiciones del modelo a partir de las observaciones. La matriz de pesos calculada es incluida en la función de costo usada para solucionar el problema inverso dinámico, y por lo tanto en la formulación del filtro de Kalman. De esta forma, se propone un filtro de Kalman ponderado que incluye la matriz de pesos. El desempeño del filtro (en términos del error de localización) se analiza para varios SNRs. El desempeño óptimo se alcanza usando el modelo lineal con matriz de ponderación calculado por el método de producto interno.
PALABRAS CLAVE: problema inverso, mapeo cerebral, matriz de ponderación.
1. INTRODUCTION
Electroencephalographic source reconstruction is a technique that estimate the sources of electrical currents (i.e. the current distribution) within the brain that give rise to recordable potential fields at the scalp. Estimation of the brain activity from electroencephalographic (EEG) measurements is known to be an ill-posed inverse problem (as there are an infinite number of different current sources that give rise to identical scalp recordings) that cannot be solved without some kind of regularization. Selection of dynamical models for neural activity as a constraint has improved the regularized solution.
However, the main restriction is the selection of the dynamical model [1]. Consequently, some variations of the dynamic model should be considered in order to improve the performance of the dynamic model for spatial and temporal behavior, such as more complex linear or nonlinear models, and temporal variability for the source and local neighbor interaction. Since the covariance is an assumption of the model in order to solve the inverse problem, the solution is highly dependent on that value. Therefore, it is necessary to improve the model from the observations and correct the considered [2].
In order to represent adequately the process dynamics, estimation of covariance from the process observation are used in [3] considering uniformly distributed variance for all current sources into the dynamic model. However, consider a uniform variance is an additional assumption that can increase the estimation error in the model since the neural activity is usually generated in a particular zone into the brain and therefore the variance is not uniform.
This article presents an EEG source reconstruction method that solves the inverse problem assuming a linear dynamic model. Additionally, a weighted Kalman filter approach is proposed where a weighting matrix is computed from the observation measurements in order to correct the model assumptions effectively representing the subjacent physiological phenomena. These models are applied over a realistic head structure. The analysis is made up from simulated EEG signals for different levels of noise.
2. MATERIALS AND METHODS
2.1. Inverse Problem Framework
The forward model for EEG data can be described by the discrete time measurement equation as follows:
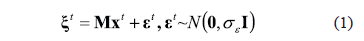
where vector 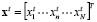 ,
, 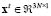 , comprises the local 3-dimensional current vectors
, comprises the local 3-dimensional current vectors 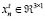 , with
, with 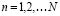 , being
, being 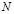 the number of distributed sources reflecting the brain activity. The so called lead field matrix,
the number of distributed sources reflecting the brain activity. The so called lead field matrix, 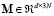 , relates the current densities
, relates the current densities 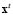 inside the brain at time instant
inside the brain at time instant 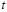 with the EEG measurements, , and can be derived using the Maxwell equations for a specific head model [2]. The vector representing the measurement noise is modeled as a (vector-valued) random variable by using both covariance matrix and cross-covariance, where notation
with the EEG measurements, , and can be derived using the Maxwell equations for a specific head model [2]. The vector representing the measurement noise is modeled as a (vector-valued) random variable by using both covariance matrix and cross-covariance, where notation 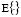 stands for the expectation operator,
stands for the expectation operator, 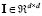 stands for the identity matrix and
stands for the identity matrix and 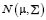 denotes a normal distribution with
denotes a normal distribution with 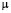 and
and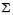 as mean and covariance matrix, respectively.
as mean and covariance matrix, respectively.
Generally, (1) represents an inverse problem and the estimation 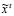 can be obtained by minimizing the objective function given for each time
can be obtained by minimizing the objective function given for each time 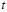 independently, as follows:
independently, as follows:
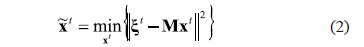
being 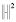 is the
is the 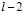 norm. However, the measured EEG comes from a process where the activity is not uniform and therefore its associate variance defined as is not uniform over all
norm. However, the measured EEG comes from a process where the activity is not uniform and therefore its associate variance defined as is not uniform over all 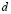 channels. It is usually considered Gaussian, with zero mean and a variance inversely proportional to the signal magnitude [4]. In order to account for inhomogeneous variance, the following weighted least squares minimization problem can be considered:
channels. It is usually considered Gaussian, with zero mean and a variance inversely proportional to the signal magnitude [4]. In order to account for inhomogeneous variance, the following weighted least squares minimization problem can be considered:
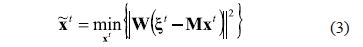
where 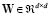 is a weighting matrix, which is diagonal in the case of uncorrelated Gaussian noise.
is a weighting matrix, which is diagonal in the case of uncorrelated Gaussian noise.
Since equation (3) is an ill-posed inverse problem, an improvement in the solution can be obtained through regularization methods by including prior information (spatial and temporal constraints) and can be formulated as follows:
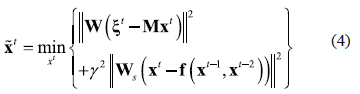
where 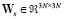 is an operator associated to the spatial constraint (selected in this case as a first order spatial derivative) and
is an operator associated to the spatial constraint (selected in this case as a first order spatial derivative) and 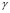 is the regularization hyper parameter [2]. Term
is the regularization hyper parameter [2]. Term 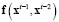 is a vectorial function that describes the second order dynamics of the current density (and thus the neuronal activity) and represent the state evolution equation. Additionally, such function is assumed to be a second order linear model defined as:
is a vectorial function that describes the second order dynamics of the current density (and thus the neuronal activity) and represent the state evolution equation. Additionally, such function is assumed to be a second order linear model defined as:
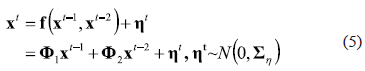
where is the so-called process noise representing the external stimulus, and the matrix denotes the covariance matrix of , i.e., . Furthermore, the random variables and with 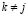 are supposed to be uncorrelated, i.e., , and where and ; with ,
are supposed to be uncorrelated, i.e., , and where and ; with , 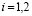 being
being 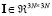 the identity matrix. Notation
the identity matrix. Notation 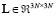 stands for the matrix operator that represents the spatial interaction among sources [3]. Equation (4) represents the solution of a dynamic inverse problem that can be solved by application of Kalman filtering methods. For that purpose, equation (5) can be reformulated in the form of a first order augmented model as follows:
stands for the matrix operator that represents the spatial interaction among sources [3]. Equation (4) represents the solution of a dynamic inverse problem that can be solved by application of Kalman filtering methods. For that purpose, equation (5) can be reformulated in the form of a first order augmented model as follows:
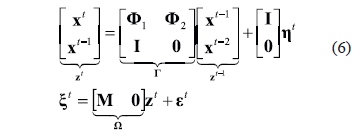
2.2. Weighting preprocessing
Typically, since 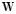 is associated with the correlation matrix of an EEG time series at time
is associated with the correlation matrix of an EEG time series at time 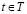 , it can be defined as a positive definite weighting matrix
, it can be defined as a positive definite weighting matrix 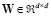 that distinguishes channels, effectively representing the subjacent physiological phenomena, and according to some evaluation measure [5]. Matrix
that distinguishes channels, effectively representing the subjacent physiological phenomena, and according to some evaluation measure [5]. Matrix 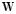 is also called a multivariable projection matrix and is defined, in the case of uncorrelated Gaussian noise, as follows:
is also called a multivariable projection matrix and is defined, in the case of uncorrelated Gaussian noise, as follows:

being, a weighting vector, where is the weight. This diagonal preponderance matrix improves the model assumptions of (1) in the solution of the dynamic inverse problem. Therefore, the estimated activity resulting from the inverse problem solution including the weighting matrix is modified correcting the covariance matrix of (1).
Since 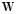 consider the variability of the EEG time series , it can be calculated from a matrix
consider the variability of the EEG time series , it can be calculated from a matrix 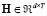 constructed as follows:
constructed as follows:
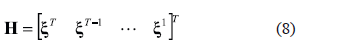
where 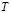 is the total number of samples.
is the total number of samples.
Consider the singular value decomposition of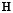 , where the diagonal entries of are the singular values of
, where the diagonal entries of are the singular values of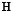 . Matrix
. Matrix 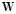 is estimated according to the following optimization problem:
is estimated according to the following optimization problem:
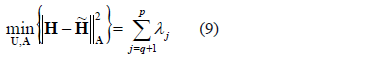
where 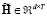 is the reconstruction matrix in a low dimensional space so that , matrix and
is the reconstruction matrix in a low dimensional space so that , matrix and 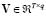 is the orthogonal projection matrix corresponding to the eigenvectors of matrix ,
is the orthogonal projection matrix corresponding to the eigenvectors of matrix , 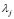 is the eigenvalue of the same matrix, and
is the eigenvalue of the same matrix, and 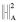 represents the squared m-inner norm regarding a matrix
represents the squared m-inner norm regarding a matrix 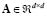 , where
, where 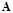 represents the distance used in the m-inner norm. Therefore, from the previous optimization problem with
represents the distance used in the m-inner norm. Therefore, from the previous optimization problem with 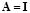 can be accomplished the following weighting vector:
can be accomplished the following weighting vector:
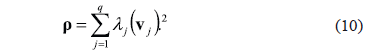
where 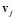 is the column of
is the column of 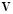 , and
, and 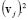 stands for each element squared. Then, corresponding weighting matrix is.
stands for each element squared. Then, corresponding weighting matrix is. 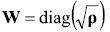
From the same framework, weighting matrix 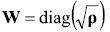 can be chosen as where vector a is obtained from
can be chosen as where vector a is obtained from 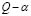 method proposed in [7]. The weight vector
method proposed in [7]. The weight vector 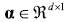 is given by:
is given by:

By replacing the distance 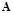 used in (9) by
used in (9) by 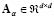 given by:
given by:

The following optimization problem is defined
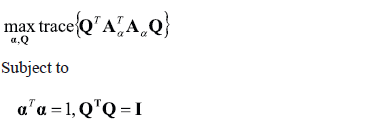
being 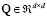 an arbitrary orthonormal matrix. The weighting vector a and the matrix
an arbitrary orthonormal matrix. The weighting vector a and the matrix 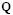 are determined at the maximal point of the optimization problem.
are determined at the maximal point of the optimization problem.
2.3. Weighted Kalman filter
Equation (4) can be solved in the Kalman filter framework, where the time update equations are defined as follows:
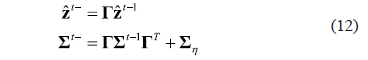
where 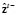 is defined as a priori estimation of
is defined as a priori estimation of 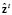 . Then, we compute the measurement update equations for the state filter described by:
. Then, we compute the measurement update equations for the state filter described by:
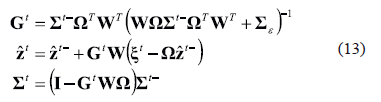
3. RESULTS AND DISCUSSIONS
3.1. Simulated EEG Recordings
Initially, system dynamics is approximated through linear time invariant model according to [6] considering anatomic constraints related with spatial coupling between sources. Testing is carried out for simulated EEG recordings. In this way, a global localization error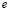 , according to [2] is used for each trial:
, according to [2] is used for each trial:

where 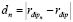 is the distance from the element position
is the distance from the element position 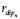 to the true source position
to the true source position 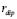 and
and 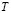 is the total number of samples.
is the total number of samples.
A global localization error is computed as a mean value of the errors for each trial, and error bars are the sample standard deviations (from the sample of 100 trials). At each source, the 3D local current density vector is mapped, to 32 electrode sites for the 10-20 system. A realistic three layer head model is used for the solution [3].
The evaluation of the inverse solution is achieved for simulated EEG data where underlying sources are known. Here, the temporal dynamics are suggested to be simulated using linear model given by (5). The parameters used for simulation are, and 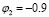 , and the activity in the source is modeled as a combination of three sine functions whose frequencies are evenly spaced in the alpha band (8 - 12 Hz), since the clinical data used in real EEG recordings display prominent alpha activity [3]. Additionally, robustness of the estimation process is analyzed when a nonlinear model is used to represent the temporal dynamics. The nonlinear temporal dynamics is suggested according to [1] to be simulated using the nonlinear model given by:
, and the activity in the source is modeled as a combination of three sine functions whose frequencies are evenly spaced in the alpha band (8 - 12 Hz), since the clinical data used in real EEG recordings display prominent alpha activity [3]. Additionally, robustness of the estimation process is analyzed when a nonlinear model is used to represent the temporal dynamics. The nonlinear temporal dynamics is suggested according to [1] to be simulated using the nonlinear model given by:
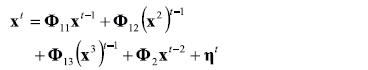
where , , and being 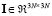 the identity matrix. The parameters used for simulation are, and
the identity matrix. The parameters used for simulation are, and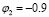 , and the activity in the source is modeled as in the linear case. Specifically, the simulated brain dynamics are generated for 1000 time points, assuming a sampling rate of 1000 Hz. Besides, the 100 repetitions of one second of synthetic EEG data are generated from the simulated current densities by multiplication with the lead field matrix
, and the activity in the source is modeled as in the linear case. Specifically, the simulated brain dynamics are generated for 1000 time points, assuming a sampling rate of 1000 Hz. Besides, the 100 repetitions of one second of synthetic EEG data are generated from the simulated current densities by multiplication with the lead field matrix 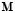 , taking into account the additive noise with six different signal noise ratios (SNRs): 1 dB, 5 dB, 10 dB, 15 dB, 20 dB and 25 dB.
, taking into account the additive noise with six different signal noise ratios (SNRs): 1 dB, 5 dB, 10 dB, 15 dB, 20 dB and 25 dB.
3.2. Weighting Analysis
The following weighting matrices are considered:
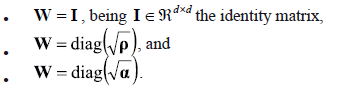
In order to consider the effect of noise level in the estimation of the weighting matrix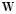 , an estimation of the weights for several SNR's is performed. This analysis is performed for matrices and with and without normalization. In Fig. 1 it is shown the preprocessing weights for several noise conditions without normalization. It is shown for the case of normalization that the variance increases its values when it is not normalized in spite of the noise levels.
, an estimation of the weights for several SNR's is performed. This analysis is performed for matrices and with and without normalization. In Fig. 1 it is shown the preprocessing weights for several noise conditions without normalization. It is shown for the case of normalization that the variance increases its values when it is not normalized in spite of the noise levels.
Figure 1. Preprocessing weights without normalization
However, as shown in Fig. 2 it is clear that the matrix values are stable for the several levels of noise in method.
Figure 2. Preprocessing weights with normalization
Additionally, it can be seen from Fig. 3 that the normalized matrix weights obtained by the 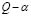 method are also stable for several levels of noise.
method are also stable for several levels of noise.
Figure 3. Preprocessing weights with normalization
In Fig. 4 is depicted the simulated and estimated neural activity for several weighting matrices at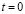 ,
, 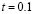 , and
, and 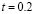 seconds. As shown in Fig. 4, when the weighted Kalman filter is applied, an improvement on the estimation is achieved for each case in comparison with
seconds. As shown in Fig. 4, when the weighted Kalman filter is applied, an improvement on the estimation is achieved for each case in comparison with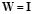 .
.
Figure 4. Brain mapping for simulated and estimated neural activity for several weighting matrices
The global localization error in case of linear and nonlinear second order models is computed using the selected weighting matrices. In Fig. 5 and Fig. 6 are shown the estimation results using the Kalman filtering for state estimation using signals simulated with non linear and linear models. It is shown that the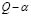 method presents the better performance with less localization error for both models.
method presents the better performance with less localization error for both models.
Figure 5. Global localization error and error bars for several weighting matrices for the nonlinear model
Figure 6. Global localization error and error bars for several weighting matrices for the linear model
Both methods and represent an alternative to measure the relevance of each considered channel and then intuitively can be used as a weighted factor, as explained in [7]. In mathematical terms, the main difference between these two methods lies in the form of the optimization problem. By considering that the first eigenvectors of are the same of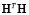 , it can be concluded that
, it can be concluded that 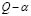 method is a quadratic form of method
method is a quadratic form of method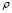 . Such quadratic form is convenient for simplicity because relevance vector can be easily calculated. In general, the weighting matrix
. Such quadratic form is convenient for simplicity because relevance vector can be easily calculated. In general, the weighting matrix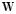 calculated through the
calculated through the 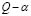 method presents better performance for brain mapping and source localization, which can be attributed to the search that this method employs. In addition, its nature and the iterative tuning of their parameters make the
method presents better performance for brain mapping and source localization, which can be attributed to the search that this method employs. In addition, its nature and the iterative tuning of their parameters make the 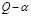 method more sensitive to significant changes of the electrical signal that goes through channels.
method more sensitive to significant changes of the electrical signal that goes through channels.
4. CONCLUSIONS AND FUTURE WORK
In this paper, we have addressed the dynamical inverse problem of EEG source reconstruction, using a new method to improve the model through a weighted approach. The obtained results demonstrate that the models with including weighting matrices perform better than the assumed model. This improvement is due to the fact that the model with weighting matrices corrects the initial assumption from observations. These results are confirmed in this paper for simulated signals over several SNR values where the weighted model using the 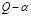 method reached the best performance. In future work, a time varying weighting matrix could be included in the Kalman filter in order to further improve the performance of the estimator.
method reached the best performance. In future work, a time varying weighting matrix could be included in the Kalman filter in order to further improve the performance of the estimator.
5. ACKNOWLEDGMENTS
This research is carried out under grants: “CENTRO DE INVESTIGACIÓN E INNOVACIÓN DE EXCELENCIA - ARTICA”, funded by COLCIENCIAS.
REFERENCES
[1] Giraldo, E., Den Dekker, A. and Castellanos-Dominguez, G., Estimation of dynamic neural activity using a kalman filter approach based on physiological models. 33rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Buenos Aires, Argentina, 10, pp. 2914-2917, 2010. [ Links ]
[2] Grech, R., Tracey, C., Muscat, J., Camilleri, K., Fabri, S., Zervakis, M., Xanthoupoulos, P., Sakkalis, V. and Vanrumste, B., Review on solving the inverse problem in EEG source analysis. Journal of Neuro Engineering and Rehabilitation, 5:25, pp. 1186-1211, 2008. [ Links ]
[3] Barton, M., Robinson, P., Kumar, A., Galka, H., Durrant-White, H., Guivant, J. and Ozaki, T., Evaluating the performance of kalman filter based EEG source localization. IEEE Transactions on Biomedical Engineering, 56, pp. 435-453, 2009. [ Links ]
[4] Rochefort, L., Liu, T., Kressler, B., Liu, J., Spincemaille, P., Lebon, V., Wu, J., Wang, Y., Quantitative susceptibility map reconstruction from MR phase data using Bayesian regularization: Validation and application to brain imaging. Magnetic Resonance in Medicine, 63, pp. 194-206, 2009. [ Links ]
[5] Delgado-Trejos, E., Perera-Lluna, A., Vallverdu-Ferrer, M., Caminal-Magrans, P. and Castellanos-Dominguez, G., Dimensionality reduction oriented toward the feature visualization for ischemia detection. IEEE Transactions on Information Technology in Biomedicine, 13, pp. 590-598, 2009. [ Links ]
[6] Robinson, J. and Kim, P., Compact dynamical model of brain activity. Phys. Rev. E, 75, pp. 031907-031917, 2007. [ Links ]
[7] Wolf, A. and Shashua, L., Feature selection for unsupervised and supervised inference: The emergence of sparsity in a weight-based approach, Journal of Machine Learning Research, 250, pp. 1855-1877, 2005. [ Links ]













