Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.80 no.182 Medellín nov./dez. 2013
OUTLIER DETECTION IN ROTATING MACHINERY UNDER NON-STATIONARY OPERATING CONDITIONS USING DYNAMIC FEATURES AND ONE-CLASS CLASSIFIERS
DETECCION DE ATIPICOS EN MAQUINAS ROTATIVAS CON CONDICIONES DE OPERACIÓN NO ESTACIONARIAS USANDO CARACTERISTICAS DINAMICAS Y CLASIFICADORES DE UNA CLASE
OSCAR CARDONA MORALES
Est.. Doctorado, Universidad Nacional de Colombia Sede Manizales, ocardonam@unal.edu.co.
DIEGO A. ÁLVAREZ MARÍN
Prof. Universidad Nacional de Colombia Sede Manizales, daalvarez@unal.edu.co
GERMAN CASTELLANOS-DOMINGUEZ
Prof. Universidad Nacional de Colombia Sede Manizales, cgcastellanosd@unal.edu.co
Received for review June 8th, 2012, accepted July 29th, 2013, final version August, 21th, 2013
ABSTRACT: The main goal of condition-based maintenance is to describe the machine state under current operating regimes, which can be non-stationary depending of load/speed changes. Besides, damaged machine data are not always available in real-world applications. This paper proposes a methodology of outlier detection in time-varying mechanical systems based on dynamic features and data description classifiers. Dynamic features set is formed by spectral sub-band centroids and linear frequency cepstral coefficients extracted from time-frequency representations. One-class classification is carried out to validate performance of the dynamic features as descriptors of machine behavior. The methodology is tested with a data set coming from a test-rig including different machine states with variable speed conditions. The proposed approach is validated on real recordings acquired from a ship driveline. The results outperform other time-frequency features in terms of classification performance. The methodology is robust to minimal changes in the machine state and/or time-varying operational conditions.
KEYWORDS: Dynamic features, One-class classification, Data description.
RESUMEN: Se propone una metodología para detección de atípicos en sistemas mecánicos variantes en el tiempo, basada en características dinámicas y descriptores de datos. El conjunto de características dinámicas está conformado mediante centroides de sub-banda espectral y coeficientes cepstrales de frecuencia lineal, ambos extraídos de representaciones tiempo-frecuencia. La clasificación de una clase es utilizada para validar el rendimiento de las características dinámicas como descriptores del comportamiento de la máquina en comparación. La metodología es probada con un conjunto de datos de un banco de pruebas con diferentes estados (normal, desbalance y desalineación), los cuales son medidos bajo condiciones de velocidad variable. El esquema propuesto es validado con registros de una línea de transmisión de un buque. Los resultados superan otras características tiempo-frecuencia en rendimiento de clasificación. La metodología es robusta a cambios mínimos en el estado de la máquina y/o condiciones de operación variantes en el tiempo.
PALABRAS CLAVE: Características dinámicas, Clasificación de una clase, Descripción de datos.
1. INTRODUCTION
In modern industries, fault detection of rotating machinery is a fundamental issue since it helps to reduce unnecessary expenditure in repairs while improving machine performance. Regarding this matter, the main challenge is to determine the current state of the machine from a set of measurements, termed Condition-Based Maintenance (CBM). The machine state is assessed usually using vibration analysis because it gives a high precision and has a low economic cost. Nonetheless, the following two problems arise: The first one appears when the machine conditions are time-varying, either by changes in speed or load, inasmuch as the vibration signals are realizations of non-stationary processes. The second problem is associated to the amount of available data characterizing different machine states, since, in most of the cases, recordings of a damaged machine are not available. The latter fact hinders the application of conventional classification techniques due to strong imbalance of the faulty/normal classes (machine states).
With regard to the former problem, some authors have used time-frequency representations (TFR) in describing the machine's dynamic behavior under non-stationary operating conditions. In particular, Sedjic et al. in [1] summarize different methods for estimating energy concentration of several TFR extracted from a set of test rig faults. But they only visually identify the qualitative difference between several faults instead of carrying out a quantitative automated classification procedure. However, inclusion of the classification stage implies high computational cost since a TFR map comprises a lot of non-relevant information that should be avoided [2]. To reduce the computational cost, authors [3] and [4] use basic statistical features (mean, standard deviation, kurtosis, and root mean square) estimated from a time series and its frequency representation. Nevertheless, those features do not properly describe the dynamic behavior generated by non-stationary operating conditions of the machine. Therefore, there is a need to carry out a methodology to characterize the machine's dynamic behavior, but at a low computational cost.
With regard to the latter problem, one-class classification (OCC) techniques have been used to determine whether the machine state ceases to be normal or first damage symptoms appear. Thus, Tax and Duin in [5] compare several commonly used one-class classifiers such as the normal distribution classifier, the k-nearest neighbor classifier, and support-vector data description (SVDD). Considered classifiers are trained and tested employing vibration signals at different constant speeds by using a set of statistical-based features, however, classification performance achieved is low. With the aim of improving the classification performance, some authors have proposed different methodologies based on estimation of statistical features from piecewise segmented non-stationary vibration signals. Among other approaches are the following: weighted SVDD [6], moving-average model [7], wavelet packet transform [8], and subspace reduction by principal component analysis (PCA) [9]. These methodologies reach high classification performance, but in practical cases such as high speed fluctuations, inherent signal segmentation implies loss of relevant information [10].
In this paper, a novel methodology for mechanical system description having non-stationary behavior is introduced. In particular, the proposed approach uses the spectral sub-band centroids and the linear frequency cepstral coefficients; all of them extracted from a TFR for machine dynamic characterization. Due to the large number of features obtained from the TFR, a feature selection process is carried out to determine the contribution of the most relevant dynamic characteristics. Finally, the resulting dynamic features are validated by OCC, whose performance is compared when extracting the whole TFR map. The proposed methodology is tested with a dataset collected in a test rig for normal, unbalanced, and misaligned assemblies. Recordings are acquired under variable speed conditions including machine start-up and coast-down. The proposed methodology is also validated over recordings of a real ship driveline.
The layout of this paper is as follows: in Section 2, a brief overview is given to describe TFR-based dynamic features and one-class approaches employed in this work for the analysis of non-stationary signals. Sections 3 and 4 bring numerical experiments of performance achieved that is compared with other state-of-the-art techniques. Discussion of the results is given in Section 5, while Section 6 provides the related conclusions and future research.
2. BACKGROUND
2.1. Frequency enhancement
Time-frequency representation determines the energy concentration along the frequency axis at a given time instant. Particularly, the Short Time Fourier Transform (STFT) introduces time localization by using a sliding window function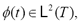 going along with the signal
going along with the signal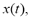 lasting
lasting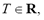 as follows:
as follows:
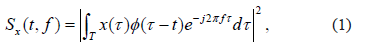
where 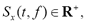 and windowing function, defined as
and windowing function, defined as 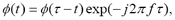 gives a relationship between the input signal,
gives a relationship between the input signal, 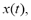 and a set of functions with the energy compacted in narrow strips of the time-frequency plane.
and a set of functions with the energy compacted in narrow strips of the time-frequency plane.
2.2. Dynamic feature extraction
In computations,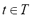 and
and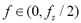 are described by discrete indexes
are described by discrete indexes 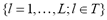 and
and 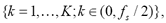 being
being 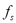 the sample frequency. Therefore, the time-frequency map dimension is
the sample frequency. Therefore, the time-frequency map dimension is 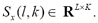 Since TFR holds a huge amount of non-relevant information, it is of primal importance to develop methods to allow extracting salient and discriminant information from the vibration signal [2].
Since TFR holds a huge amount of non-relevant information, it is of primal importance to develop methods to allow extracting salient and discriminant information from the vibration signal [2].
Taking into account that TF analysis models a signal spectral density as a time function under the assumption that the spectral content remains stationary within small time intervals of computation, then short-time parameters extracted from TFR can be considered. Among feature extraction methods, adequate candidates are the Spectral Sub-band Centroids (SSC) [11] and the Linear Frequency Cepstral Coefficient (LFCC) [12]. In both cases, TFR-based short-time parameters are extracted using a filter-bank decomposition, which efficiently combines frequency and magnitude information from the short-term power spectrum input signals. Time-variant outputs of these filters that might be chosen so as to cover the most relevant part of the frequency range are regarded as the set of time-variant features, denoted as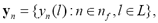
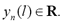
Therefore, sampled vectors over discrete time, 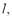 of each narrow-band feature,
of each narrow-band feature, 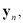 are obtained using filter bank modeling. For instance, the set of LFCC is extracted based on the Discrete Cosine Transform of triangular log-filter banks,
are obtained using filter bank modeling. For instance, the set of LFCC is extracted based on the Discrete Cosine Transform of triangular log-filter banks,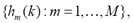 which are linearly spaced in the frequency domain:
which are linearly spaced in the frequency domain:
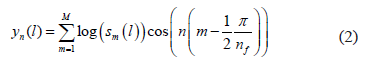
where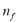 is the number of desired LFCC features, and
is the number of desired LFCC features, and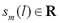 is the weighted sum of each frequency filter response set that is given as:
is the weighted sum of each frequency filter response set that is given as:
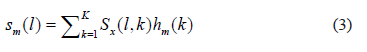
Another effective way of generating time-frequency based time-variant features can be achieved through computation of the SSC histograms that are estimated for each filter in the frequency domain,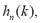 as:
as:
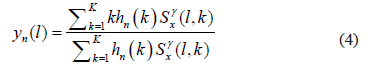
where parameter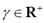 represents the spectrum dynamic range used in centroid computation, and
represents the spectrum dynamic range used in centroid computation, and 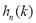 are the filters linearly distributed along the spectrum. In addition, the energy neighboring each centroid can be also considered as a time-variant feature that for a fixed bandwidth
are the filters linearly distributed along the spectrum. In addition, the energy neighboring each centroid can be also considered as a time-variant feature that for a fixed bandwidth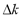 is computed in the form:
is computed in the form:
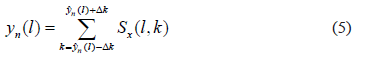
where 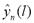 is the actual value of the time-variant centroid estimated by (4).
is the actual value of the time-variant centroid estimated by (4).
2.3. One-class data inference
Based on optimal signal detection inferring whether the signal is present, different approaches to distinguish one class from the rest of the data feature space, 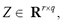 have been developed, being r the input data dimension and q the number of available objects. Particularly, the measured data space is related to just one of the considered classes (termed target) that can be properly characterized as well as compactly clustered, in such a way as to guarantee discrimination of other possible objects (that is, a non-target cl ass for which no measurements are available) distributed outside of the target class. So, to circumscribe the target class within concrete bounds two concepts are introduced: a) distance,
have been developed, being r the input data dimension and q the number of available objects. Particularly, the measured data space is related to just one of the considered classes (termed target) that can be properly characterized as well as compactly clustered, in such a way as to guarantee discrimination of other possible objects (that is, a non-target cl ass for which no measurements are available) distributed outside of the target class. So, to circumscribe the target class within concrete bounds two concepts are introduced: a) distance,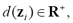 measuring closeness between an object,
measuring closeness between an object,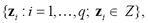 and the target class, and b) the distance threshold,
and the target class, and b) the distance threshold, 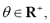 fixing the decision boundary of the target class, that is:
fixing the decision boundary of the target class, that is:
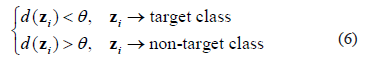
Thus, definition of adequate classification boundary around target class remains the most important issue. Moreover, the threshold 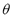 should accept as many objects as possible from the target class, while minimizing chance of accepting non-target (or outlier) objects [5]. In practice, distance complexity ranges from simplest Euclidean to more elaborate ones, for instance, statistical-based distances. Regarding the former distance, it may have several restrictions when describing a low density volume of the hyper-sphere. Instead, the latter distances are more robust since they impose a model to the OCC providing a highly dense volume of the decision hypersphere. Specifically, for implementing the OCC, the Gaussian distribution classifier (using Mahalanobis distance) and the Support Vector Data Description (using kernel based square distance) are convenient in machine state classification.
should accept as many objects as possible from the target class, while minimizing chance of accepting non-target (or outlier) objects [5]. In practice, distance complexity ranges from simplest Euclidean to more elaborate ones, for instance, statistical-based distances. Regarding the former distance, it may have several restrictions when describing a low density volume of the hyper-sphere. Instead, the latter distances are more robust since they impose a model to the OCC providing a highly dense volume of the decision hypersphere. Specifically, for implementing the OCC, the Gaussian distribution classifier (using Mahalanobis distance) and the Support Vector Data Description (using kernel based square distance) are convenient in machine state classification.
So, the Gaussian-distribution-based OCC fits a r-dimensional multivariate normal distribution to the data set [13]:
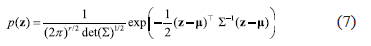
where notations 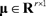 and
and 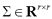 stand for the mean vector and covariance matrix of the training set, Z. To distinguish between target and outlier data, a threshold on the probability distribution function is set. Afterwards, for a new sample object,
stand for the mean vector and covariance matrix of the training set, Z. To distinguish between target and outlier data, a threshold on the probability distribution function is set. Afterwards, for a new sample object,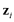 , the Mahalanobis distance is calculated as
, the Mahalanobis distance is calculated as  .
.
The 5% of instances with the largest Mahalanobis distance , are regarded as outliers. As a result, an ellipsoidal boundary close to the data is achieved. Yet, this method works reasonably well when the data is normally distributed
Support vector data description is an OCC algorithm that identifies samples not covering the same space region as the training sample [5]. The algorithm computes a spherically shaped decision boundary by solving the following quadratic optimization problem:
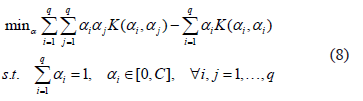
where C is a parameter indicating how severely objects outside the sphere should be penalized; 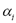 are Lagrange multipliers for solving (6). In addition, K represents a Mercel kernel that usually is a Gaussian kernel, defined as
are Lagrange multipliers for solving (6). In addition, K represents a Mercel kernel that usually is a Gaussian kernel, defined as 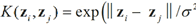 where
where 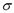 is the standard deviation as an adjustable parameter, being
is the standard deviation as an adjustable parameter, being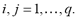 Vectors located outside the sphere, are termed bounded support vectors for which
Vectors located outside the sphere, are termed bounded support vectors for which 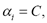 while objects with
while objects with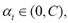 are termed unbounded support vectors, being located exactly on the surface of the decision boundary sphere.
are termed unbounded support vectors, being located exactly on the surface of the decision boundary sphere.
Then, the introduced squared distance of an object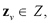 to the center of the sphere is estimated, as follows:
to the center of the sphere is estimated, as follows:
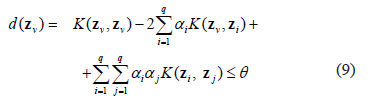
In consequence, the threshold, 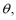 is the radius calculated as the distance from the sphere center to an unbounded support vector. In practice, the average distance to a set of unbounded support vectors is used. Besides, the SVDD parameters can be fixed as mentioned in [15].
is the radius calculated as the distance from the sphere center to an unbounded support vector. In practice, the average distance to a set of unbounded support vectors is used. Besides, the SVDD parameters can be fixed as mentioned in [15].
3. EXPERIMENTAL ANALYSIS
The proposed methodology for novelty detection using dynamic features that are extracted from TFR appraises the following stages: a) TFR enhancement of the input vibration signal, b) feature estimation of dynamic features, c) dimension reduction by means of latent variable decomposition, and d) machine diagnosis inference based on the OCC scheme. It must be noted that two different experiments are supplied: firstly, when data is collected from an experimental test rig, and secondly, when data is acquired from a real ship port driveline.
3.1. Collected database from experimental test rig
A set of experiments is performed with the supplied test rig shown in Fig. 1, which includes a 2 HP Siemens electromotor with 1800rpm maximum speed. The motor is connected to the shaft using a rigid coupling. The shaft has two supports, each one with a SKF-6005 NR ball bearing and two drilling wheels designed for simulating either static or dynamic unbalance. The vibration signals are acquired by ACC102 accelerometer, with a measurement range of 0-10kHz and 100mV/g of sensibility. The National Instruments USB-6009 data acquisition card is employed at 20kHz sampling frequency.
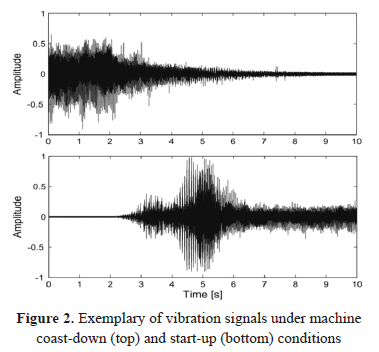
The data set holds the following types of acquired outliers regarding the considered machine states: a) two static and one dynamic unbalance, and b) two angular and two parallel misalignment. The data collection also includes an undamaged condition type, which is taken as the only target class. The machine state is measured for start-up and coast-down conditions, where each recording under coast-down condition (Fig. 2-top) appraises three phases: a) maximum speed (1800 rpm), b) turning motor off, and c) steady-state regime. The start-up condition case (Fig. 2-bottom) has the same phases, but in reverse order. Each recording is ten-seconds long. It is worth noting that considered working phases are not synchronized each to other, that is, the second phase may begin at different times within each recording.
As a result, 20 recordings were acquired at horizontal measurement point for each one of the 8 considered types of machine states, i.e., in total 160 recordings were collected for operating condition. In order to reduce the computational cost and taking into that the maximum spectral information is around 1.2kHz, the recordings are subsampled down to 4 kHz, obtaining a recording length of L=40000 samples in 10 seconds.
3.2. TFR based Enhancement
The TFR matrix holds dimension 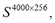 where K=256 is chosen as to exceed reasonable resolution of 0.1Hz. Fig. 3 shows the spectral decomposition of each signal under coast-down (top) and start-up (bottom) conditions. As seen, spectral components contract/expand with decreasing/increasing rotational speed. The coast-down condition allows showing, in a proper way, the harmonic relation between the different spectral components, which contribute with a visual inspection to distinguish machine behavior.
where K=256 is chosen as to exceed reasonable resolution of 0.1Hz. Fig. 3 shows the spectral decomposition of each signal under coast-down (top) and start-up (bottom) conditions. As seen, spectral components contract/expand with decreasing/increasing rotational speed. The coast-down condition allows showing, in a proper way, the harmonic relation between the different spectral components, which contribute with a visual inspection to distinguish machine behavior.
In contrast, under the start-up condition, spectral information clearly gathers around 300Hz during 2 seconds after turning on the electromotor. This behavior is caused by an unbalance of electromagnetic forces inside the electromotor
associated to the stator and the winding. Therefore, the actual contribution of spectral components on the shaft is hidden.
3.3. Estimation and dimension reduction of dynamic feature set
In the beginning, a set appraising n SSC as well as n LFCC features is extracted from each estimated TFR. Based on [14], the needed number of dynamic features in (2) and (4), initially, is fixed to be 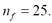 Besides, other free parameters needed for dynamic feature estimation are fixed empirically. Namely, in case of LFCC features,
Besides, other free parameters needed for dynamic feature estimation are fixed empirically. Namely, in case of LFCC features, 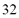 triangular filters comprise the log-filter bank used, which are linearly spaced in the frequency band. Likewise, the SSC features are estimated using a dynamic range, i.e.,
triangular filters comprise the log-filter bank used, which are linearly spaced in the frequency band. Likewise, the SSC features are estimated using a dynamic range, i.e., , to preserve the spectral power of the TFR. Consequently, 50 dynamic features are extracted from considered TFR, where each one having 40000 samples of length. From the above, a huge dynamic feature set is computed and it follows that there is a need for an adequate dimension reduction. In these cases, space reduction is provided stepwise: Firstly, each dynamic feature is to be adequately
, to preserve the spectral power of the TFR. Consequently, 50 dynamic features are extracted from considered TFR, where each one having 40000 samples of length. From the above, a huge dynamic feature set is computed and it follows that there is a need for an adequate dimension reduction. In these cases, space reduction is provided stepwise: Firstly, each dynamic feature is to be adequately
represented by a set of scalar-valued statistical moments, that is,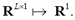 Secondly, the obtained feature space matrix has dimension
Secondly, the obtained feature space matrix has dimension 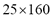 for each considered TFR. Specifically, a multivariate latent approach is used to select the data set to be fed into the one-class classifier. Lastly, we determine the optimal number of features,
for each considered TFR. Specifically, a multivariate latent approach is used to select the data set to be fed into the one-class classifier. Lastly, we determine the optimal number of features, 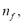 that are required to properly characterize the vibration signal, in as much as this parameter controls computational cost as well as performance within the classification framework. To select an adequate number of features, the following criterion of multivariate reconstruction error holds:
that are required to properly characterize the vibration signal, in as much as this parameter controls computational cost as well as performance within the classification framework. To select an adequate number of features, the following criterion of multivariate reconstruction error holds:
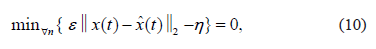
where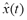 is the reconstructed signal,
is the reconstructed signal,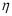 is a small enough real positive value,
is a small enough real positive value, 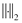 is the norm squared value, and
is the norm squared value, and 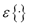 stands for the expectation operator. As a result, the minimum number of LFCC features to achieve an explained variance value equal to
stands for the expectation operator. As a result, the minimum number of LFCC features to achieve an explained variance value equal to 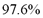 is
is 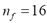 , while
, while 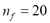 for SSC parameters are needed to reach a variance of
for SSC parameters are needed to reach a variance of 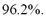
3.4. Target class classification validated on test rig data
Testing of the discussed training methodology, outlined in Section 2.3, is carried out for identification of target class in either considered machine condition: start-up and coast-down.
For classifier validation, the OCC error performance is computed using the commonly used 10-fold cross-validation procedure, where the target data is split into 70% for training and the rest 30% is merged with the outlier data (non-target class). To measure classifier performance both specificity and sensibility are used.
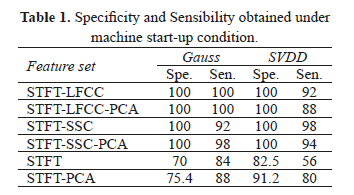
Table 1 shows classification performance for the start-up condition. As seen, the STFT-LFCC brings the best performance regardless of the considered classifier. Nonetheless, it is worth noting that higher performance is achieved using the Gauss classifier since it does not misclassify outliers while preserving the highest value of achieved sensibility.
For the sake of comparison, performance values are also computed for whole TFR maps, the achieved values in this case exhibit worse outcomes.
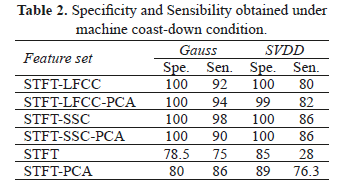
As regards the validation for the coast-down machine regime, achieved performance is shown in Table 2. The STFT-LFCC and the STFT-SSC achieve the best value no matter if the PCA-based dimension reduction is applied. Again, the Gauss classifier outperforms SVDD when proposed dynamic features are used. Lastly, the TFR maps set holds the worse performance.
4. NOVEL DETECTION IN SHIP DRIVELINE APPLICATION
The proposed methodology is tested also on the ship port driveline, which has a Caterpillar 3412C diesel engine with the following characteristics: 12 valves in Vee, 4 strokes and a maximum speed of 2100 rpm. The engine is directly coupled with a gearbox MG-520. The database is acquired using a ACC102 accelerometer with a measurement range of 0-8kHz and 10 mV/g of sensibility.
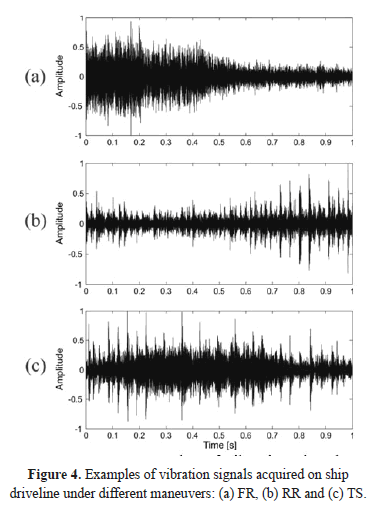
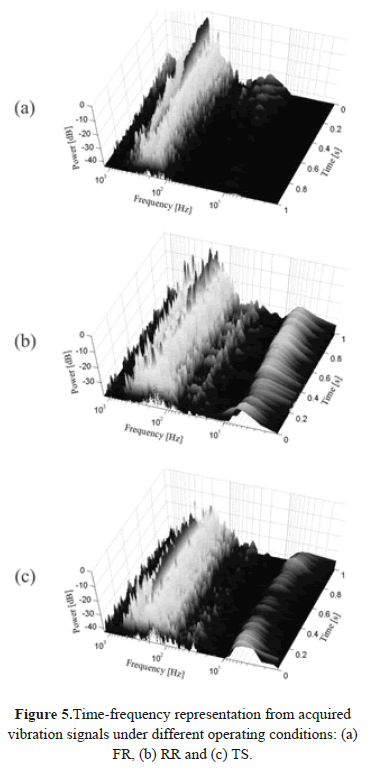
The sensor is located between the engine and the gearbox to capture the information coming from the drive and gearbox. ANI9234 acquisition card is employed using a sampling frequency of 25.6 kHz. The recordings are captured under several operating conditions: forward-running (FR), reverse-running (RR) and turn starboard (TS). For each operating condition are acquired 159, 137 and 163 recordings, respectively. An example of the acquired vibration signals is shown in Fig. 4.
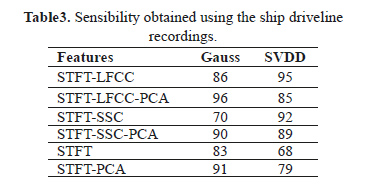
Fig. 5 shows the time-frequency representation from measured signals on the ship driveline. In case of FR (Fig. 5(a)), a decrement in the speed can be seen despite the fact that the ship is running forward. This fact implies speed changes due to the induced load by the sea movement. In case of RR (Fig. 5(b)) and TS (Fig. 5(c)), several spectral components present peaks in short-time instants, which can be associated to the bearing frequency, however, without faulty signals it is difficult to assesses whether the behavior corresponds to an abnormal machine state. Therefore, a one-class classification procedure allows the machine state to be inferred and described. Table 3 shows the estimated classifier performance for data collected from the real ship driveline application.
The STFT-LFCC feature set turns out to be the better set again, but after using PCA as well as the Gaussian classifier. As a result, STFT-LFCC feature set gets the highest sensibility value.
It is worth noting that in the concrete case of ship driveline application, the whole TFR map achieves high performance when the Gaussian classifier is used. Yet, the computational cost is increased.
4. DISCUSSION
After testing the discussed methodology of fault detection in rotating machinery, the following assertions can be stated regarding the extracted dynamic features and the employed one-class classifiers:
- Use of feature sets related with TFR concentration energy may lead to a high performance of outlier detection. Yet, the whole TFR map does not allow the generalization capability of classifier in distinguishing between target and outlier samples to be improved. Therefore, this type of features may face serious restrictions to be considered in fault detection. Instead, the proposed dynamic features achieve better performance and reduce computational burden. As a result, dynamic features can contribute to building an effective automatic CBM system.
- Comparison between both considered dynamic features, LFCC and SSC, infer that the former set is more consistent in terms of achieving high performance, as observed throughout all experiments carried out. This fact makes sense since cepstrum, as a vibration signal feature, brings proper representation about mechanical processes [14]. Besides, taking into account that the proposed methodology accomplishes cepstrum estimation in non-stationary conditions, provided (by dynamic feature set) relevant information allows describing better machine dynamic behavior.
- The usefulness of PCA for multivariate dimension reduction is another aspect to highlight. When the kernel-based classifiers are used, PCA projection provides a data linear transformation that may damage classifier performance. Tables 1, 2, and 3 show that target class performance (sensibility), using PCA, is equal or is lower to the one obtained when PCA is not employed. Therefore, to achieve high performance, inclusion of PCA is not necesary and rather it increases substancially the computational burden.
- In the case of one-class classifiers, mostly, the Gauss classifier presents better performance than SVDD meaning that the data follow a normal distribution, as mentioned in [5]. Nonetheless, achieved performance using SVDD can be improved if properly tuning its parameters. This adjustment, which implies parameter optimizing during each classification iteration, increases computational cost.
5. CONCLUSIONS
A methodology for outlier detection in rotating machinery under non-stationary operating conditions is proposed. The methodology improves the characterization of dynamic behavior allowing high performance of target class classification to be achieved. The proposed characterization process is based on the dynamic features extrated from time-frequency representations. As a result, the methodology overcomes the obtained performance by means the whole TFR map. In general, the proposed dynamic features allow reducing computational cost and distinguishing classes with different time-variant behavior. Besides, proposed dynamic features can be used for either rejecting outliers or accepting targets. Future work includes validating the proposed methodology in other mechanical systems.
ACKNOWLEDGEMENTS
The authors acknowledge to Colciencias for the financial support of the research project with code "1101-521-28792". Also they would like to thank the Universidad Nacional de Colombia with the research project "Análisis tiempo-frecuencia de señales de vibraciones mecánicas para detectar fallos en máquinas rotativas".
REFERENCES
[1] Sejdic, E., Djurovic, I. and Jiang, J., Time-frequency feature representation using energy concentration: An overview of recent advances. DSP, 19(1), pp. 153 - 183, 2009. [ Links ]
[2] Cardona-Morales, O., Angel-Orozco, A. and Castellanos-Domínguez, G., Damage detection in vibration signals using non parametric time-frequency representations. ISMA2010, 2010. [ Links ]
[3] Honarvar, F. and Martin, H.R., New statistical moments for diagnostics of rolling element bearings. Journal of MS&E, 119(3), pp. 425-432, 1997. [ Links ]
[4] Lei, Y., He, Z. and Zi, Y., A new approach to intelligent fault diagnosis of rotating machinery. E.S. with A,. 35(4), pp.1593 - 1600, 2008. [ Links ]
[5] Tax, D.M.J. and Duin, R.P.W., Support Vector Data Description. ML, 54(1), pp.45-66, 2004. [ Links ]
[6] Zhang, Y., Liu, X-D., Xie, F-D. and Li, K-Q., Fault classifier of rotating machinery based on weighted support vector data description. E.S. with A, 36(4), pp.7928 - 7932, 2009. [ Links ]
[7] Mcbain, J. and Timusk, M., Fault detection in variable speed machinery: Statistical parameterization.JS&V, 327(3-5), pp. 623 - 646, 2009. [ Links ]
[8] Pan, Y., Chen, J. and Li, X., Bearing performance degradation assessment based on lifting wavelet packet decomposition and fuzzy c-means. MSSP, 24(2), pp. 559 - 566, 2010. [ Links ]
[9] Mcbain, J. and Timusk, M., Feature extraction for novelty detection as applied to fault detection in machiney. PRL, 32(7), pp. 1054 - 1061, 2011. [ Links ]
[10] Bartkowiak, A. and Zimroz, R., Outliers analysis and one class classification approach for planetary gearbox diagnosis. J. of P.:, 305(1):012031, 2011. [ Links ]
[11] Paliwal, K.K., Spectral subband centroids as features for speech recognition. IEEE Workshop om ASR&U, pp. 124 -131, 1997. [ Links ]
[12] Rabiner, L. and Juang, B.H., Fundamentals of Speech Recognition. Prentice Hall, Englewood Cliffs, NJ, 1993. [ Links ]
[13] Bishop, C., Neural Networks for Pattern Recognition, Oxford University Press, Walton Street, Oxford OX2 6DP, 1995. [ Links ]
[14] Nelwamondo, F., Marwala, T. and Mahola, U., Early classification of bearing faults using Hidden Markov Models, Gaussian Mixture Models, Mel Frequency Cepstral Coefficients and Fractals, 2005. [ Links ]
[15] Alvarez-Meza, A., Daza-SantaColoma, G., Acosta-Medina, C. and Castellanos-Dominguez, G., Parameter selection in least squares-support vector machines regression oriented, using generalized cross-validation. DYNA, 79, pp. 23-30, 2011. [ Links ]