Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.185 Medellín maio/jun. 2014
http://dx.doi.org/10.15446/dyna.v81n185.36039
Dynamic stability of slender columns with semi-rigid connections under periodic axial load: verification and examples
Estabilidad dinámica de columnas esbeltas con conexiones semirrígidas bajo carga axial periódica: verificación y ejemplos
Oliver Giraldo-Londoño a & J. Darío Aristizábal-Ochoa b
a Structural Researcher, M.S. Ohio University, USA ogirald86@gmail.com.
b 125-Year Generation Professor, Ph.D. School of Mines, National University. Medellin, Colombia jdaristi@unal.edu.co
Received: December 15th, de 2012. Received in revised form: December 20th, 2013. Accepted: December 26th, 2013.
Abstract
The dynamic stability of an elastic prismatic slender column with semirigid connections at both ends of identical stiffness and with sidesway between the two ends totally inhibited, subject to parametric axial loads including the combined effects of rotary inertia and external damping was presented in a companion paper. Closed-form expressions that predict the dynamic instability regions of slender columns were developed by making use of Floquet's theory. The proposed equations are straightforward and simple to apply. The proposed solution is capable of capturing the phenomena of stability of columns under periodic axial loads using a single column element. The proposed method and corresponding equations can be used to investigate the effects of damping, rotary inertia and semirigid connections on the stability analysis of slender columns under periodically varying axial loads. Sensitivity studies are presented herein that show the effects of rotary inertia, damping and semirigid connections on the dynamic stability of columns under parametric axial loads. Analytical studies indicate that the dynamic behavior of columns under periodic loading is strongly affected by the flexural stiffness of the end connections and the external damping, but not so much by the rotary inertia. Three examples are presented in detail and the calculated results are compared with those reported by other researchers.
Keywords: Buckling, Columns, Dynamic Analysis, Damping, Semi-Rigid Connections, Parametric Loading, Periodic Loading. Stability.
Resumen
La estabilidad dinámica de una columna elástica prismática esbelta con conexiones semirrígidas en ambos extremos de rigidez idéntica y con desplazamiento lateral entre los dos extremos totalmente inhibido sujetos a cargas axiales paramétricas incluyendo los efectos combinados de inercia rotacional y amortiguación externas fue presentada en una publicación adjunta. Expresiones cerradas que se pueden utilizar para predecir las regiones inestabilidad dinámica de columnas esbeltas se desarrollan haciendo uso de la teoría de Floquet. Las ecuaciones propuestas son sencillas y fáciles de aplicar. La solución propuesta es capaz de capturar el fenómeno de estabilidad en columnas sometidas a cargas axiales periódicas utilizando un solo elemento de columna. El método propuesto y las ecuaciones correspondientes se pueden utilizar para investigar los efectos del amortiguamiento, la inercia rotacional de la columna, y las conexiones semirrígidas en el análisis de estabilidad de columnas esbeltas sometidas a cargas axiales periódicas. Estudios de sensibilidad presentados en esta publicación muestran los efectos de la inercia rotacional, el amortiguamiento y las conexiones semi-rígidas en la estabilidad dinámica de columnas sometidas a cargas axiales paramétricas. Los estudios analíticos indican que el comportamiento dinámico de columnas bajo carga periódica está fuertemente afectado por la rigidez a la flexión de las conexiones de los dos apoyos y por el amortiguamiento externo, pero no tanto por la inercia rotacional. Tres ejemplos se presentan en detalle y los resultados calculados se comparan con los reportados por otros investigadores.
Palabras claves: pandeo, columnas, análisis dinámico amortiguado, conexiones semirígidas, cargas paramétricas, cargas periódicas, estabilidad.
1. Introduction
The main objective of this paper is to present examples and sensitivity studies to verify an analytical method and closed-form equations presented in a companion paper that determine the dynamic stability of an elastic 2D prismatic column with semirigid connections with sidesway between the two ends totally inhibited, subject to parametric axial load described by a Fourier series. The proposed model and corresponding equations which are straightforward and relatively simple to apply can be used to investigate the effects of damping, rotary inertia and semirigid connections on the stability of slender columns under periodically varying axial loads using a single column element. The closed-form equations make use of Floquet's theory to predict the dynamic instability regions of slender columns. Sensitivity studies and three verification examples are included in this paper that shows the effects of rotary inertia, damping and semirigid connections on the dynamic stability of prismatic columns under parametric axial loads.
2. Sensitivity study
2.1. Dynamic Instability Regions for Damped Columns Subjected to Harmonically Varying Axial Loads
In this section closed-form expressions are developed that determine the first two instability border lines for columns subjected to periodic loads given by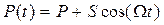 .
.
Knowing the values of 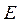 ,
, 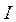 ,
, 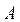 ,
, 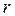 ,
, 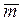 ,
, 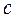 and
and 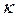 the non-dimensional parameters, discussed in step (4) of the companion paper, can be calculated. In this particular case the normalized axial load is written as
the non-dimensional parameters, discussed in step (4) of the companion paper, can be calculated. In this particular case the normalized axial load is written as 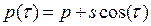 , where:
, where: 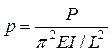 ,
, 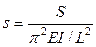 , and
, and 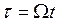 . This would correspond to
. This would correspond to 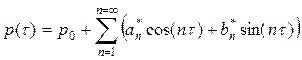 with
with 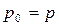 ;
; 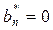 (with
(with 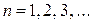 );
); 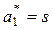 ; and
; and 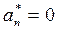 (with
(with 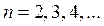 ). To determine the instability border lines, solutions with period
). To determine the instability border lines, solutions with period 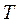 and
and 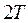 must be considered.
must be considered.
The closed-form expression for the region of instability corresponding to the solution with period 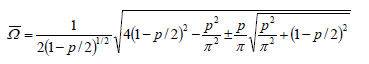 can be found by substituting the corresponding values of
can be found by substituting the corresponding values of  ;
;  , and
, and  into Eq. (9) presented in the companion paper as follows:
into Eq. (9) presented in the companion paper as follows:
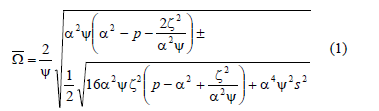
Now consider the solution with period 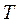 . The closed-form expression for the instability region is obtained by substituting the corresponding values of
. The closed-form expression for the instability region is obtained by substituting the corresponding values of 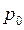 ;
; 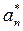 , and
, and 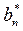 into Eq. (10) presented in the companion paper as follows:
into Eq. (10) presented in the companion paper as follows:
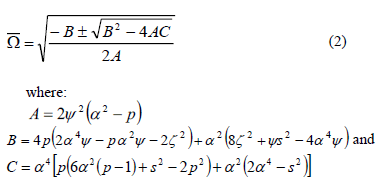
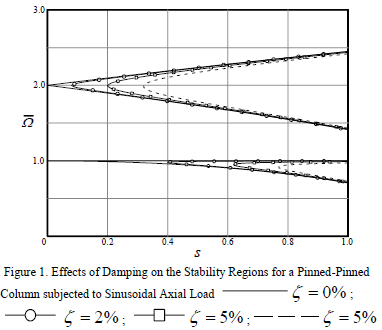
Sensitivity studies for different values of the damping parameter, rotary inertia parameter, and fixity factor are carried out. Fig. 1 shows the effect of damping in the dynamic instability regions taking 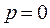 and
and  (or
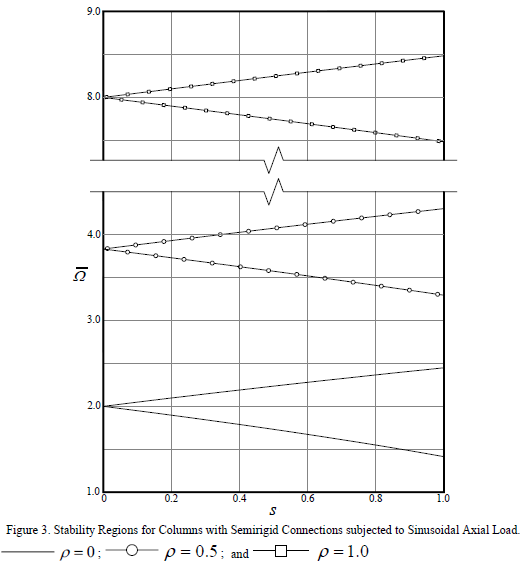
(or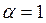 ) in Eqs. (1) and (2). Numerical results indicate that by increasing the damping, the region of instability moves from left to right acquiring some curvature as reported by Svensson [2] and Timoshenko and Gere [3]. Fig. 4 shows the variation of the region of instability corresponding to Eq. (1) for different values of slenderness parameter. The effects of the stiffness of the end connections on the instability regions are shown in Fig. 5.
) in Eqs. (1) and (2). Numerical results indicate that by increasing the damping, the region of instability moves from left to right acquiring some curvature as reported by Svensson [2] and Timoshenko and Gere [3]. Fig. 4 shows the variation of the region of instability corresponding to Eq. (1) for different values of slenderness parameter. The effects of the stiffness of the end connections on the instability regions are shown in Fig. 5.
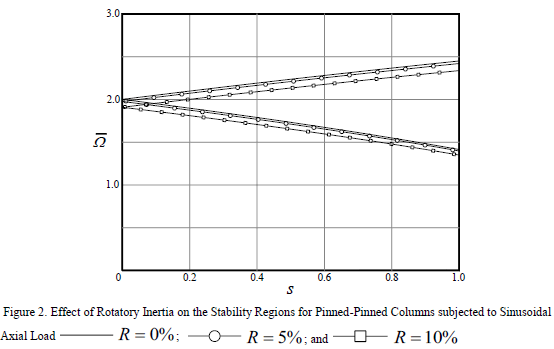
Fig. 2 and 3 indicate that: 1) the effects of rotary inertia on the dynamic response of slender columns subject to periodic axial loads are negligible for reasonable values of slenderness; and 2) the dynamic instability of a slender column subject to a periodic loading is greatly affected by the stiffness of the end connections.
3. Comprehensive examples and verification
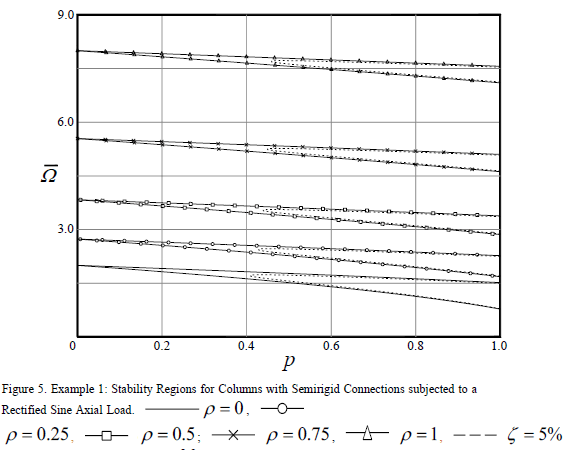
Example 1: Column with Semi-rigid Connections subjected to Rectified Sine Axial Load
Determine the stability regions for a damped column elastically connected at both ends, given that: 1) the fixity factor of the connections are: 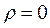 ,
, 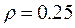 ,
,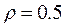 ,
, 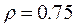 , and
, and 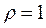 ; 2) the damping parameter is
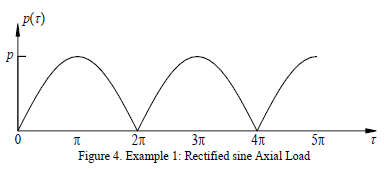
; 2) the damping parameter is 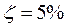 ; and 3) the applied axial load is given by a rectified sine wave as shown in Fig. 4.
; and 3) the applied axial load is given by a rectified sine wave as shown in Fig. 4.
Solution: The first necessary step to carry out the dynamic analysis of a slender column with semirigid connections is to determine the parameter 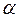 , which depends only of the fixity factor
, which depends only of the fixity factor 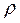 . By solving numerically Eq. 7b the values obtained are:
. By solving numerically Eq. 7b the values obtained are: 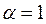 ,
,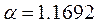 ,
, 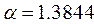 ,
, 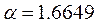 , and
, and 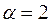 , for the respective values of the fixity factor. Now, to evaluate the instability regions the expansion in Fourier series for the given axial load must be known. The coefficients of the series are:
, for the respective values of the fixity factor. Now, to evaluate the instability regions the expansion in Fourier series for the given axial load must be known. The coefficients of the series are: 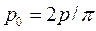 ,
, 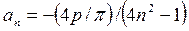 ,
, 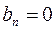 . Closed expressions for the two first regions of instability are obtained by substituting the values of
. Closed expressions for the two first regions of instability are obtained by substituting the values of 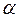 ,
, 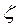 and the corresponding terms of the Fourier series into Eqs. (9) and (10) presented in the companion paper.
and the corresponding terms of the Fourier series into Eqs. (9) and (10) presented in the companion paper.
a) Solution with period 2T

b) Solution with period T
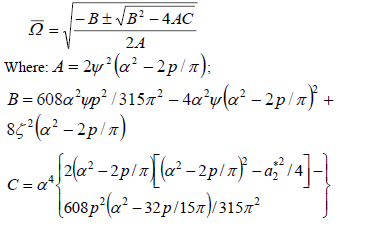
Fig. 5 shows the two first regions of instability for the prismatic column described above. Results indicate that under damping, regions of instability move horizontally showing that a minimal value of the magnitude of the applied axial load is necessary to make the system unstable. According as the fixity factor of the connections increases, the minimal value of the applied axial load also moves horizontally. As the connection becomes stiffer, results also show that the principal region becomes narrower.
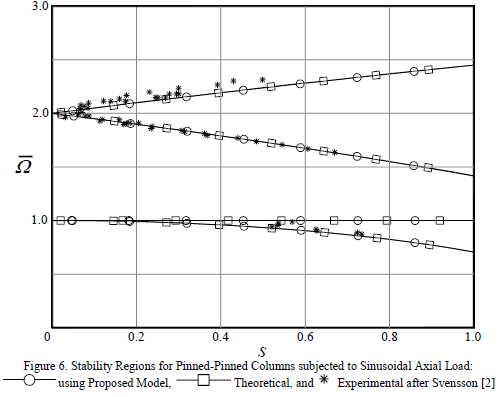
EXAMPLE 2: Dynamic stability regions of a hinged-hinged column under periodic loading
Determine the stability limits for a perfectly hinged-hinged steel column. Assume that: it has a 1mmx25mm rectangular cross section, L= 400 mm, and the applied axial load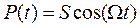 . Compare the results using the proposed method with those reported by Svensson [2]. Neglect the effects of damping.
. Compare the results using the proposed method with those reported by Svensson [2]. Neglect the effects of damping.
Solution: Note that the values of E, I, A, r, 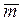 are known,
are known, 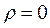 (hinged at both ends),
(hinged at both ends), 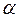 = 1 and
= 1 and 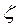 = 0 (damping effects are neglected).
= 0 (damping effects are neglected).
From step (4) the normalized function 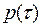 can be written as
can be written as 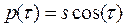 with
with 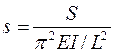 . Therefore for the expression
. Therefore for the expression 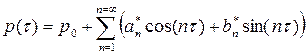 to be satisfied, then
to be satisfied, then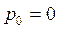 ,
, 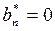 ,
, 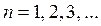 ,
, 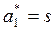 , and
, and 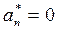 ,
, 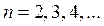
Closed expressions for the first two regions of instability are obtained by substituting p= 0,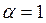 , and
, and 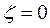 into Eqs. (12) and (13). Therefore:
into Eqs. (12) and (13). Therefore:
a) Solution with period 2T
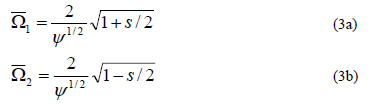
b) Solution with period T
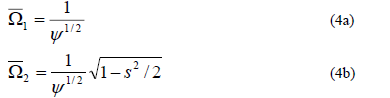
The first two stability regions can be found simply by increasing the values of s from zero to 1 and plotting the four roots obtained from Eqs. (3) and (4). Fig. 6 shows these regions and the results are in accordance with those calculated and reported by Svensson [2]. His experimental results are also shown.
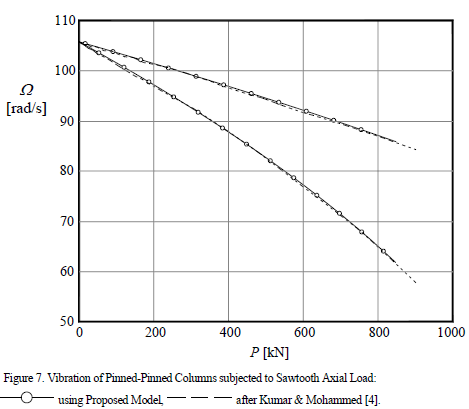
Example 3: Pinned-Pinned column subjected to saw-tooth Axial Load
A slender column subject to a saw-tooth periodic axial load described by Kumar and Mohammed [4] is considered. The periodic load is defined by case 4 listed in Table 1 of the companion paper. The corresponding Fourier coefficients are: 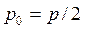 ,
, 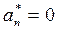 , and
, and 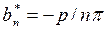 . Assume that: L= 7 m, E=2.1x1011 Pa and I=2.003x10-5m4.
. Assume that: L= 7 m, E=2.1x1011 Pa and I=2.003x10-5m4.
Notice that: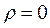 ,
, 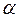 = 1,
= 1, 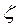 = 0 and
= 0 and 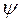 = 1 (since the effect of rotary inertia is neglected). Thus, the following equations for the two first regions of instability can be obtained:
= 1 (since the effect of rotary inertia is neglected). Thus, the following equations for the two first regions of instability can be obtained:
a) Solution with period 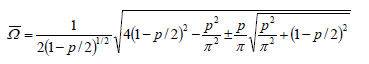
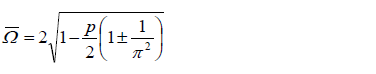
b) Solution with period 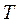
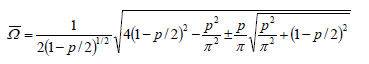
Fig. 7 shows the principal region of instability that corresponds to the solution with period 2T. It can be seen that the obtained results using the proposed method are practically identical to those reported by Kumar and Mohammed [4] obtained using the FEM
4. Summary and conclusions
Closed-form expressions that can be used to predict the dynamic instability regions of slender Euler-Bernoulli columns were developed in a companion paper using Floquet's theory. The proposed method is straightforward and the corresponding equations are relatively easy to use. The proposed closed-form equations enable the analyst to explicitly evaluate the effects of damping, semirigid connections, and rotary inertia on the nonlinear elastic response and lateral stability of slender prismatic columns with sidesway inhibited subject to static and dynamic axial loads. The proposed equations are not available in the technical literature. A sensitivity study and three examples are presented in detail that illustrate how to analyze the dynamic stability of slender prismatic columns with sidesway totally inhibited as the frequency and magnitude of the axial load varies.
Analytical results and sensitivity studies indicate that the second-order dynamic response of a slender Euler-Bernoulli column subject to periodic axial loads is affected by the rotary inertia, external damping, and the stiffness of the end connections. It was found that for slender columns the effects of rotary inertia are not as strong as those produced by damping and the stiffness of the end connections. Analytical results indicate that: 1) instability border lines move horizontally and acquire some curvature as the damping increases; 2) as the stiffness of the end connections increases, the frequencie of the applied axial load defining the instability border lines also increase; and 3) the column axial deflection in the instability regions decreases significantly as the fixity factor 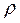 varies from zero (i.e. for perfectly pinned-pinned columns) to one (i.e. for perfectly clamped-clamped columns). These results are in accordance with those reported by other researchers.
varies from zero (i.e. for perfectly pinned-pinned columns) to one (i.e. for perfectly clamped-clamped columns). These results are in accordance with those reported by other researchers.
Acknowledgments
The authors wish to thank the Department of Civil Engineeering of the School of Mines of the National University of Colombia at Medellín and to COLCIENCIAS for their financial support.
Notation
The following symbols are used in both this paper and the companion paper:
A = area of the column cross section;
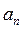 ,
, 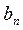 ,
, 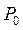 = coefficients of Fourier series utilized to describe the applied axial load;
= coefficients of Fourier series utilized to describe the applied axial load;
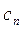 ,
, 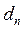 = constants;
= constants;
c = Damping coefficient;
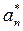 ,
, 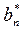 ,
, 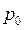 = dimensionless coefficients of Fourier series utilized to describe the applied axial load;
= dimensionless coefficients of Fourier series utilized to describe the applied axial load;
E = Young's modulus of the material;
f(t) = Amplification function for lateral deflection of the column;
I = Principal moment of inertia about its plane of bending of the column;
L = Column span;
M = Bending moment along the column;
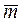 = Uniform mass per unit of length of the column (including any additional uniformly distributed mass);
= Uniform mass per unit of length of the column (including any additional uniformly distributed mass);
P(t) = Periodic axial load applied at the ends of the column;
p(t) = Dimensionless axial load;
r = Radius of gyration of the column cross section;
R = Slenderness parameter;
V = Shear force;
y(x, t) = Column lateral deflection;
a = Parameter used to describe the shape function of the column;
k = Stiffness of the rotational restraint at both ends of the column;
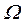 = Angular frequency of the applied axial load;
= Angular frequency of the applied axial load;
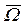 = Angular frequency of the applied axial load normalized with respect to
= Angular frequency of the applied axial load normalized with respect to 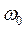 ;
;
r = Fixity factor at the ends A' and B' of the column;
q = Rotation of the cross section due to bending;
t = Dimensionless time parameter;
w0 = Natural frequency of lateral vibration of a simply supported beam without axial load;
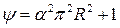 = Dimensionless parameter;
= Dimensionless parameter;
z = Dimensionless damping parameter.
References
[1] Giraldo-Londoño, O. and Aristizabal-Ochoa, J. D., Dynamic stability of slender columns with semi-rigid connections under periodic axial load: Theory, Revista DYNA, accepted for publication, 2013. [ Links ]
[2] Svensson, I., Dynamic Instability regions in a Damped System, J. of Sound and Vibration, 244 (5), pp. 779-793, 2001. [ Links ]
[3] Timoshenko S. P. and Gere, J. M., Theory of Elastic Stability, 2nd Ed., McGraw-Hill Book Inc., New York, N.Y, 1961 [ Links ]
[4] Kumar, T. H. and Mohammed A., Finite element analysis of dynamic stability of skeletal structures under periodic loading," J. of Zhejiang University SCIENCE A, Vol. 8 (2), 245-256, 2007. http://www.springerlink.com/content/e03352h0h1712153/ [ Links ]
Oliver Giraldo-Londoño received the BS in Civil Engineering in 2010 from Universidad Nacional de Colombia, Sede Medellin, and the MS in Structural Engineering in 2014 from Ohio University at Athens, OH, USA. From 2006-2009, he worked as undergraduate teacher assistant for the department of mathematics at Universidad Nacional de Colombia, Sede Medellin. From 2010-present, he has been working in the Structural Stability Research Group (GES) at Universidad Nacional de Colombia, Sede Medellin, under the supervision of Dr. J. Dario Aristizabal-Ochoa. From 2011-2012, he worked as instructor of statics of structures and numerical methods at Universidad de Antioquia. From 2012-present, he has been working as graduate assistant at Ohio University at Athens, OH, USA. He was awarded the Emilio Robledo award (Colombian Society of Engineers, 2009) and the Young Researcher award (COLCIENCIAS, 2010-2011). Also, he was COLFUTURO scholar (2012-2014). His research interests include analysis and design of steel and concrete structures, non-linear mechanics, finite element modeling, bridge engineering, earthquake engineering, and structural dynamics.
J. Dario Aristizabal-Ochoa, received the Bachelor degree in Civil Engineering in 1970 with honors from the National University of Colombia. Medellin, Colombia, the MS and PhD degrees in Structural Engineering in 1973 and 1976, respectively from the University of Illinois at Champaign–Urbana, USA. From 1977 to 1978, he worked for the Portland Cement Association, Skokie, Illinois, USA as Structural Researcher. From 1978-1981 he worked as Marketing Manager of Seismic Applications for MTS Systems at Eden Prairie, Minnessota, USA. From 1981-1995 as Professor for the Universities of Vanderbilt at Nashville, Tennessee and for the California State University at Fullerton California, USA. Currently, he is full Professor and director of the Structural Stability Research Group at the National University of Colombia at Medellin. He was awarded the "Engineering Foundation" grant in 1982 by the American Institute of Civil Engineers (ASCE), the Raymond Reese Structural award by the American Concrete Institute (ACI) in 1984, and two NSF research grants in 1988 and 1989. Currently, he is a Full Professor in Civil Engineering, School of Mines, and National University of Colombia at Medellin. He is an active editorial member and reviewer of several international Journals (ICE, ASCE, ACI, PCI, ELSEVIER, etc). His research interests include: steel, reinforced concrete structures, structural dynamics and stability, composite materials, analysis and design of bridges, nonlinear analysis, seismic design, soil-structural interaction. His research work is referenced by numerous textbooks and construction codes (ACI, AISC, ASSHTO) and technical papers.