Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.185 Medellín maio/jun. 2014
https://doi.org/10.15446/dyna.v81n185.37244
http://dx.doi.org/10.15446/dyna.v81n185.37244
Discrete Particle Swarm Optimization in the numerical solution of a system of linear Diophantine equations
Optimización por Enjambre de Partículas Discreto en la Solución Numérica de un Sistema de Ecuaciones Diofánticas Lineales
Iván Amaya a, Luis Gómez b & Rodrigo Correa c
a PhD( c), Universidad Industrial de Santander, Colombia. ivan.amaya2@correo.uis.edu.co
b BSc on Electronics Engineering, Physicist, Universidad Industrial de Santander, Colombia. luisgomezardila@gmail.com
c Professor, PhD School of Electric, Electronic and Telecommunication Engineerings, Universidad Industrial de Santander, Colombia. crcorrea@uis.edu.co
Received: February 25th, 2013. Received in revised form: January 31th, 2014. Accepted: April 3th, 2014.
Abstract
This article proposes the use of a discrete version of the well known Particle Swarm Optimization, DPSO, a metaheuristic optimization algorithm for numerically solving a system of linear Diophantine equations. Likewise, the transformation of this type of problem (i.e. solving a system of equations) into an optimization one is also shown. The current algorithm is able to find all the integer roots in a given search domain, at least for the examples shown. Simple problems are used to show its efficacy. Moreover, aspects related to the processing time, as well as to the effect of increasing the population and the search space, are discussed. It was found that the strategy shown herein represents a good approach when dealing with systems that have more unknowns than equations, or when it becomes of considerable size, since a big search domain is required.
Keywords: Linear Diophantine equations; objective function; optimization; particle swarm.
Resumen
El presente artículo propone utilizar una versión discreta del bien conocido algoritmo metaheurístico de optimización por enjambre de partículas, DPSO, para solucionar numéricamente un sistema de ecuaciones Diofánticas lineales. Así mismo, se muestra la transformación de este tipo de problema (es decir, la solución de un sistema de ecuaciones), en uno de optimización. El presente algoritmo es capaz de encontrar todas las raíces enteras en un dominio de búsqueda dado, al menos para los ejemplos mostrados. Se utilizan algunos problemas sencillos para verificar su eficacia. Además, se muestran algunos aspectos relacionados con el tiempo de procesamiento, así como con el efecto de incrementar la población y el dominio de búsqueda. Se encontró que la estrategia mostrada aquí representa una propuesta adecuada para trabajar con sistemas que tienen más incógnitas que ecuaciones, o cuando se tiene un tamaño considerable, debido a que se requiere un gran dominio de búsqueda.
Palabras clave: Ecuaciones Diofánticas lineales; enjambre de partículas; función objetivo; optimización.
1. Introduction
With each passing day is easier to see the boom that the modeling and description of systems have generated in science and engineering, especially through Diophantine equations. Areas such as cryptography, integer factorization, number theory, algebraic geometry, control theory, data dependence on supercomputers, communications, and so on, are some examples [1]. Moreover, there is a strong mathematical foundation for this type of equations and their solutions (both, at a fundamental and at an applied level). These vary from the fanciest and most systematic approaches, up to the most recursive ones, but it is evident that there is no unified solution process, nor a single alternative for doing so. Furthermore, some equations may have a single solution, while others may have an infinite number, or, possibly, may not even have a solution in the integer or rational domains. This also applies for linear systems with this kind of equations (i.e. Diophantine ones) [2]. Matiyasevich, during the early 90s, proved that it was not possible to have an analytic algorithm that allows to foresee if a given Diophantine equation has, an integer solution , or not [3]. This problem may have been one of the engines that have boosted the search for numerical alternatives.
In order to solve a system of linear Diophantine equations, a variable elimination method (which is quite similar to Gauss's) is a good approach for small systems, but it becomes demanding for bigger ones. The specialized literature report some methods like those based on the theory of modules over main ideal domains, which are somewhat more systematic when looking for all the solutions of a given system, but, likewise, become too complex when dealing with big systems of equations [4], [5]. Some authors have previously proposed the solution of a Diophantine equation through artificial intelligence algorithms [6], [7]. This article proposes to solve, in case the solution exists in the given search domain, a linear system of Diophantine equations. Initially, some basic and necessary related concepts are laid out, and then the viability of using the numeric strategy is shown through some examples.
2. Fundamentals
A linear Diophantine equation, with 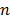 unknowns, is defined by eq. (1), where
unknowns, is defined by eq. (1), where 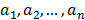 are known rational, or integer, numbers, and
are known rational, or integer, numbers, and 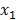 ,
,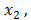 …,
…,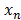 are unknowns, i.e., the numbers that should satisfy them, [8];
are unknowns, i.e., the numbers that should satisfy them, [8];  is a known integer. It is said that the integers
is a known integer. It is said that the integers 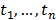 are a solution for eq. (1) if, and only if,
are a solution for eq. (1) if, and only if, 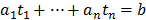 .
.
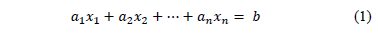
One of the basic results of number theory that can be applied to a linear Diophantine equation is the following theorem, which allows determining whether it has a solution or not (even if it is not able to calculate it):
Theorem 1. Let  be integers, where all
be integers, where all  not zeros, and let
not zeros, and let 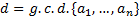 be the g.c.d. of the numbers
be the g.c.d. of the numbers 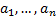 . Therefore,
. Therefore, 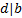 if, and only if, exist
if, and only if, exist 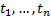 integers, such that
integers, such that 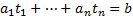 .
.
Thus, the problem of determining whether a linear Diophantine equation has a solution or not, is reduced to showing if the greatest common divisor of the 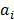 coefficients divide
coefficients divide  or not. Consider the case of two unknowns, for example, with an equation as the one shown by eq. (2), where
or not. Consider the case of two unknowns, for example, with an equation as the one shown by eq. (2), where 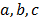 are known integers, and whose solution only exists if the g.c.d. of
are known integers, and whose solution only exists if the g.c.d. of 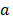 and
and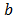 is a divisor of
is a divisor of 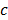 .
.
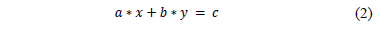
According to the previously mentioned theorem, this equation has integer solutions, and it can be shown that if 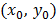 is a particular one, then all its solutions are given by eq. (3), where
is a particular one, then all its solutions are given by eq. (3), where 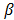 is an integer and
is an integer and 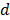 is an integer which represents the g.c.d.
is an integer which represents the g.c.d.
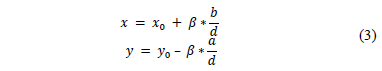
Therefore, if a linear Diophantine equation with two unknowns has a solution in the integers, then it has infinite solutions of this kind. Even so, the problem now transforms in finding a particular solution, which can be done using the following method.
Let  be a non-empty subset of
be a non-empty subset of 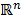 and consider eq. (4), where
and consider eq. (4), where 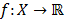 is a function.
is a function.
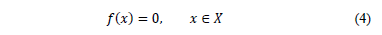
The problem of finding all the possible solutions for eq. (4) in the subset 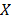 can be transformed into a global optimization problem over
can be transformed into a global optimization problem over 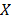 as follows:
as follows:
Let 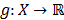 be defined by:
be defined by:
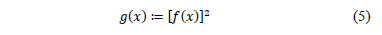
Then, for every 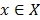 it holds that
it holds that 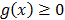 .
.
Theorem 2. Suppose that eq. (4) has a solution in 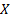 , and let
, and let 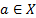 . Therefore,
. Therefore, 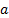 is a solution for eq. (4) if, and only if,
is a solution for eq. (4) if, and only if, 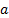 minimizes the function
minimizes the function 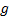 defined in (5).
defined in (5).
An immediate consequence of the previous theorem is that if eq. (4) has a solution in 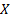 , then the global minimum of
, then the global minimum of 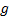 defined in (5) exists and is zero; even more, the following theorem exists:
defined in (5) exists and is zero; even more, the following theorem exists:
Theorem 3. If the function 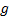 defined in (5) has a global minimum in
defined in (5) has a global minimum in 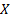 and this value is zero, then eq. (4) has a solution in
and this value is zero, then eq. (4) has a solution in 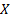 . Moreover, all global minimizers of
. Moreover, all global minimizers of 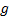 are solutions of eq. (4).
are solutions of eq. (4).
Then, if for 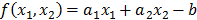 a region of the plane can be determined, where a global minimum of function
a region of the plane can be determined, where a global minimum of function 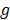 , defined by (5), and its value is zero, then any global minimizer with integer coordinates, should it exist, serves as a particular solution of eq. (2). Thus, the choice of the region is quite important to enclose, at least, a solution with integer coordinates.
, defined by (5), and its value is zero, then any global minimizer with integer coordinates, should it exist, serves as a particular solution of eq. (2). Thus, the choice of the region is quite important to enclose, at least, a solution with integer coordinates.
2.1. System of linear equations
Consider the following system of 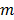 linear Diophantine equations, with unknowns
linear Diophantine equations, with unknowns 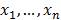 .
.
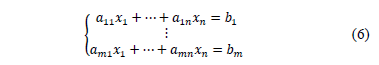
According to theorem 1, in order for the system (6) to have a solution, it is necessary, but not sufficient, that each of the 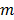 equations have a solution; this is equivalent to establishing if for each
equations have a solution; this is equivalent to establishing if for each 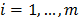 it holds that
it holds that 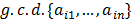 divides
divides 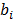 .
.
To see why this condition is not sufficient, consider the system of Diophantine equations defined by
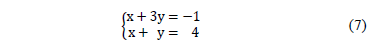
Each equation from this system has a solution in the integer domain, but the system does not have a solution as a whole. Then, and in the same way that with systems of equations in real variables, the fact that one of the equations of a system has a solution, does not imply that the whole system also has.
Even so, a method that generalizes finding all the roots (in case they exist) of a system of equations over a given set, is shown below.
Let 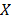 be a non-empty subset of
be a non-empty subset of 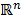 and consider the system of equations (8), where for each
and consider the system of equations (8), where for each 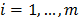 ,
, 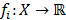 is a function.
is a function.
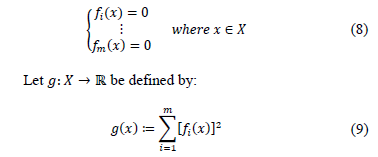
Then for all 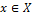 it holds that
it holds that 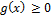 . The following result is achieved:
. The following result is achieved:
Theorem 4. Suppose that the system of equations (8) has a solution in 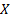 , and let
, and let 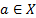 . Then,
. Then, 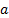 is a solution of the system (8) if, and only if,
is a solution of the system (8) if, and only if, 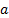 minimizes the function
minimizes the function 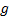 defined in (9).
defined in (9).
The general condition of the theorem 4 about the feasibility of solving the system (8) is important, since it is possible that the function 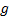 defined in (9) can be globally minimized but that the system (8) does not have a solution.
defined in (9) can be globally minimized but that the system (8) does not have a solution.
An immediate consequence of theorem 4 is that if the system (8) has a solution in 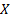 , then the global minimum of
, then the global minimum of 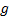 defined in (9) exists and it is zero; moreover, the following result exists:
defined in (9) exists and it is zero; moreover, the following result exists:
Theorem 5. If the function 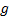 defined in (9) has a global minimum in
defined in (9) has a global minimum in 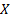 and this value is zero, then the system (8) has a solution in
and this value is zero, then the system (8) has a solution in 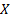 . Moreover, all global minimizers of
. Moreover, all global minimizers of 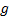 are solutions of the system (8).
are solutions of the system (8).
Therefore, for the function 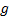 defined in (9), if there does not exist a global minimum in
defined in (9), if there does not exist a global minimum in 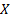 or if it exists but is different from zero, then the system of equations (8) does not have a solution in
or if it exists but is different from zero, then the system of equations (8) does not have a solution in 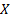 .
.
A basic result of the mathematical analysis of the algorithm establishes that if 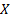 is a compact set (i.e. closed and bounded) and
is a compact set (i.e. closed and bounded) and 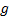 is continuous over
is continuous over 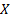 then the global minimum exists. Now, for
then the global minimum exists. Now, for 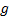 to be continuous in
to be continuous in 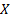 it is enough that each
it is enough that each 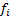 is continuous in
is continuous in 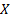 .
.
For the case of systems of Diophantine equations, unlike the particular case of an equation with two unknowns, the fact that a solution exists does not imply that others do, and even less that an infinite number exists.
For the search of possible solutions of a system of Diophantine equations, it must hold that the set 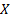 have points with integer coordinates, i.e. that
have points with integer coordinates, i.e. that 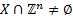 .
.
2.2. The algorithm
The implemented algorithm is built up from various interconnected blocks and is similar to the structure of traditional PSO (for real numbers), [9], [10]. A first stage is given by the random assignation of a swarm of user defined integers. Any size can be used here. Likewise, the definition of these values is subject to previous knowledge of the objective function (fitness), as well as to the presence of restrictions. Moreover, an initial speed of zero can be defined for the particles. After that, the algorithm evaluates, in the given search space, the objective function. With it, local and global best values are established, and both, speed and position, of each particle, are reevaluated as shown below. This procedure is iterative and is repeated until the convergence criteria are met, or until all solutions in the search domain are found.
An algorithm, considered as a variant of the traditional PSO, was used, [9]. In the same fashion as said PSO, its version for discrete solutions includes two vectors 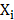 and
and 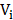 , related to the position and speed of each particle, for every iteration. The first one is a vector of random numbers, initially, in a valid solution interval. The second one can also be a random vector, but it can be assumed as zero for the first iteration, in order to keep it simple. When the problems become multidimensional, the vectors transform into a position and a speed matrices, since there is a value for each unknown, [9], [11]. Discrete PSO differs from its traditional version in which the new speed and position depend on both, an equation and a decision rule, which chooses among the local and global best values for the next iteration. Assuming there is a vector
, related to the position and speed of each particle, for every iteration. The first one is a vector of random numbers, initially, in a valid solution interval. The second one can also be a random vector, but it can be assumed as zero for the first iteration, in order to keep it simple. When the problems become multidimensional, the vectors transform into a position and a speed matrices, since there is a value for each unknown, [9], [11]. Discrete PSO differs from its traditional version in which the new speed and position depend on both, an equation and a decision rule, which chooses among the local and global best values for the next iteration. Assuming there is a vector 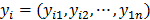 that allows the transition between continuous and discrete PSO, and which takes the value of (-1, 1, or, 0) according to eq. (10), where
that allows the transition between continuous and discrete PSO, and which takes the value of (-1, 1, or, 0) according to eq. (10), where 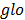 is the global optimum of the swarm, and
is the global optimum of the swarm, and 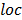 the local one, [9].
the local one, [9].
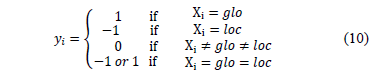
Afterwards, speed is updated according to eq. (11), where 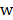 is known as the inertia factor, which is used to limit the speed of the particles;
is known as the inertia factor, which is used to limit the speed of the particles; 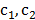 are constants which is usually are considered as equal to two; and
are constants which is usually are considered as equal to two; and 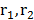 are random numbers between zero and one [10].
are random numbers between zero and one [10].
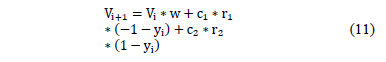
Then, the decision parameter, vector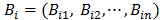 , is calculated according to eq. (12).
, is calculated according to eq. (12).
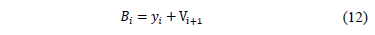
This parameter decides if the next position of the particle is chosen as the local or global best, or if it is chosen as a random number in the search domain. Thus, position update is done according to eq. (13), where 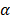 is a constant that defines the intensification (new position equal to the local or global bests) and the diversification (new position equal to a random number) [9].
is a constant that defines the intensification (new position equal to the local or global bests) and the diversification (new position equal to a random number) [9].
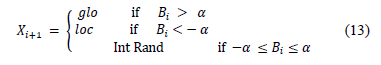
3. Results and Analysis
This section shows the results achieved after solving some systems of linear Diophantine equations, as an example of the method. A computer with an AMD Turion X2 Dual Core RM-72 processor, at 2.1 GHz, and with 4 GB of RAM memory, was used. During all the examples, the following parameters were used: w = 0.75, c1 = 0.8, c2 = 0.2, y, 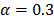 . These values were chosen based on some preliminary tests and on the information available in the literature [1], [9].
. These values were chosen based on some preliminary tests and on the information available in the literature [1], [9].
3.1. System of equations A
It is required to solve the system given by eq. (14), in the set of positive integers, which represents the amount of animals bought by a farmer and its cost. The full statement of the problem is as follows: "A farmer spent 10.000.000 COP, on 100 animals: chickens (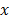 ), pigs (
), pigs (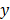 ) and cows (
) and cows (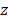 ). if he bought the chickens at 5.000 COP, pigs at 100.000 COP and cows at 500.000 COP, and if he acquired animals of all three classes, how many did he buy of each one?" [12].
). if he bought the chickens at 5.000 COP, pigs at 100.000 COP and cows at 500.000 COP, and if he acquired animals of all three classes, how many did he buy of each one?" [12].
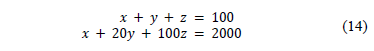
This system is equivalent, by Gaussian reduction, to the

Its general solution is given by: 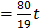 , y
, y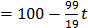 ,
, 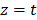 , which for
, which for 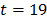 yields:
yields: 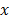 = 80;
= 80;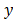 = 1;
= 1;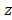 = 19. In order to solve this problem with the discrete PSO algorithm, the following objective function is created:
= 19. In order to solve this problem with the discrete PSO algorithm, the following objective function is created:
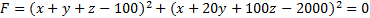
After 20 runs of the algorithm, with a swarm of 1000 particles, the same answer was always achieved. Their duration, however, varied from 1.186 s, with 204 iterations, and up to 474.043 s, with 66832 iterations. It can then be concluded that, for this system, the algorithm delivers an answer with excellent precision and accuracy, even though the number of iterations and the duration were variable. It was found that their relationship is quite close to linearity (R2=0.9955).
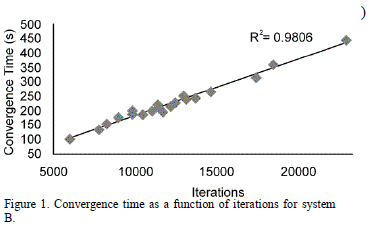
3.2. System of equations B
Afterwards, the system of seven linear Diophantine equations shown by (15) was solved, which represents a closed-loop control system, with unitary feedback, and where it is required to find the controller (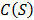 ), with six poles at
), with six poles at 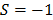 for the plant
for the plant 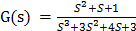 .
.
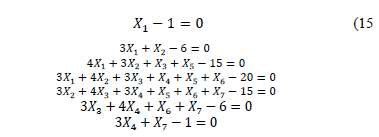
The solution of the system can be found to be:
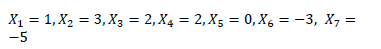
From the first equation, 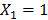 ; and from the second one,
; and from the second one, 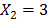 . The third equation yields
. The third equation yields  , while from the fifth and sixth equations,
, while from the fifth and sixth equations,  , which means that
, which means that 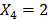 . Thus, the last equation provides
. Thus, the last equation provides 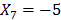 . Substracting the fourth and fifth equations,
. Substracting the fourth and fifth equations, 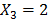 is obtained, which means that
is obtained, which means that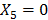 . Finally, the sixth equation yields
. Finally, the sixth equation yields 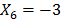 . In order to solve it through the algorithm, the following objective function was defined:
. In order to solve it through the algorithm, the following objective function was defined:
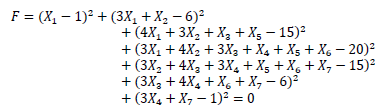
Once again, 1000 particles were used and the algorithm was run 20 times. As a result, the same answer is achieved, so it is important to remark the excellent quality of the results (in terms of accuracy and precision), as well as, the variability in time and iterations, when looking for all the solutions in the integer domain. When compared to the previous system, it can be seen that the convergence time increased, and an almost linear relation between iterations and time can be seen in Fig. 1.
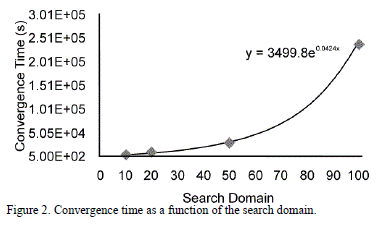
3.3. System of equations C
For this case a system of 12 linear Diophantine equations was selected:
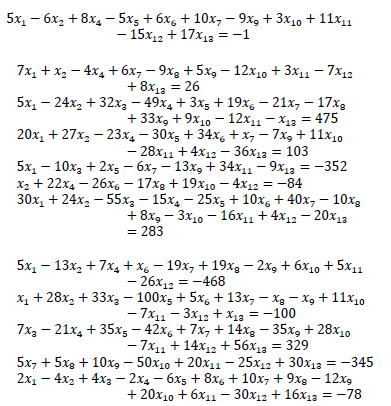
whose solution is:
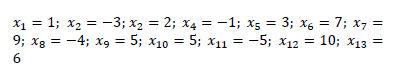
The objective function is, once again, built using the squared sum of each equation. A search space between -10 and 10 was defined, and 100 particles were used. On the same computer, an excellent quality answer (in terms of accuracy and precision) was found, but it required an average time of 129632 s (around 36 hours) and 1026435 iterations. It is worth mentioning that it was not possible to find these roots by using commercial software nor through traditional means. Fig. 2 shows the exponential increment in time, when expanding the search domain.
3.4. System of equations D
In order to further test the algorithm's effectiveness, some other Diophantine systems were used. However, in this case they do not have a solution in the set of integers, e.g. the system given by eq. (16), which has a range A = range (A ,C) = 2, and a g.c.d. (2,1,3) = g.c.d (8,-;5,-;3) = 1| { 7,11}.
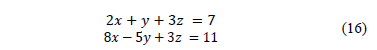
The discrete PSO algorithm reports that after 20 or more runs, for different swarm sizes and parameters, it was not possible to find an answer. It was also observed that if a system, e.g. the one given by eq. (17), has infinite solutions, a search domain must be defined, striving to locate solutions over this given set.
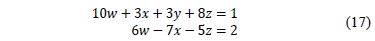
4. Conclusions
This research proved that it is possible to numerically solve a system of linear Diophantine equations through an optimization algorithm. Also, it was observed that it is possible to solve this optimization problem without using conventional approaches. It was shown, through some simple examples, that, at least for these systems, solutions with high precision and accuracy are achieved. Moreover, it was found that the convergence time and the number of iterations are random variables that mainly depend on factors such as the algorithm parameters, the initial swarm and the size of the system. Obviously, when solving a squared, small system, traditional approaches, including the ones found in most of the commercial mathematical software, are far quicker, even those that find all the roots of the system. However, in case that it is required to solve a system with more unknowns than equations, a typical situation, they are out of the question. Likewise, if the system is of a considerable size, the convergence time drastically increases, since a big search domain is required (a case found during the current research), so the numerical strategy proposed here gains importance as a possible solution alternative.
References
[1] Abraham, S., Sanyal, S., and Sanglikar, M., Particle Swarm Optimization Based Diophantine Equation Solver, ArXiv, pp.1–15, Mar. 2010. [ Links ]
[2] Bonilla E., M., Figueroa G., M., and Malabare, M., Solving the Diophantine Equation by State Space Inversion Techniques?: An Illustrative Example, Proceedings of the 2006 American Control Conference, pp.3731–3736, 2006. [ Links ]
[3] Matiyasevich, Y. V., Hilbert's Tenth Problem. MIT Press, , 1993. [ Links ]
[4] Wu - Shr-Hua. Time-varying feedback systems design via Diophantine equation order reduction, thesis (Ph.D. on Electrical Engineering), United States, The University of Texas at Arlington, 2007, pp. 1–140. [ Links ]
[5] Cohen, H., Number Theory, Vol. I: Tools and Diophantine Equations and Vol. II: Analytic and Modern Tools. Springer-Verlag, New York, 2007. [ Links ]
[6] Lugar, G., Artificial Intelligence: Structures and Strategies for Complex Problem Solving. Addison-Wesley, Boston, 2006. [ Links ]
[7] Abraham, S. and Sanglikar, M., Finding Numerical Solution to a Diophantine Equation: Simulated Annealing as a Viable Search Strategy, Proceedings of the International Conference on Mathematical Sciences, 2, pp.703–712, 2008. [ Links ]
[8] Contejean, E., An Efficient Incremental Algorithm for Solving Systems of Linear Diophantine Equations, Information and Computation, (113), pp.143–172, 1994. [ Links ]
[9] Jarboui, B., Damak, N., Siarry, P., and Rebai, A, A combinatorial particle swarm optimization for solving multi-mode resource-constrained project scheduling problems, Applied Mathematics and Computation, 195 (1), pp.299–308, Jan. 2008. [ Links ]
[10] Amaya, I., Cruz, J., and Correa, R., Real Roots of Nonlinear Systems of Equations Through a Metaheuristic Algorithm, Revista Dyna, 78 (170), pp.15–23, 2011. [ Links ]
[11] Amaya, I., Cruz, J., and Correa, R., Solution of the Mathematical Model of a Nonlinear Direct Current Circuit Using Particle Swarm Optimization, Revista Dyna, 79 (172), pp.77–84, 2012. [ Links ]
[12] Gonzáles - F. J. Ecuaciones Diofánticas, thesis (Apuntes de Matemática Discreta), Universidad de Cádiz, 2004, pp. 353–354. [ Links ]
I. Amaya, received his bachelor degree on Mechatronics Engineering from Universidad Autónoma de Bucaramanga, Bucaramanga, Santander (Colombia). Currently, he is with the School of Electrical, Electronic and Telecommunications Engineerings and is pursuing his PhD on Engineering at Universidad Industrial de Santander, Bucaramanga, Santander (Colombia). His research interests include global optimization and microwaves. ORCID: 0000-0002-8821-7137
L. Gómez, received his bachelor degree on Physics from Universidad Industrial de Santander Bucaramanga, Santander (Colombia), and also a bachelor degree on Electronics Engineering from the same University. His research interests include global optimization and Diophantine equations.
R. Correa, received his bachelor degree on Chemical Engineering from Universidad Nacional de Colombia, Bogotá, Cundinamarca (Colombia), and his master degree on Chemical Engineering from Lehigh University, Bethlehem, Pensilvania (USA) and from Universidad Industrial de Santander, Bucaramanga, Santander (Colombia). He received his PhD from Lehigh University on Polymer Science and Engineering and is currently a professor at Universidad Industrial de Santander. His research interests include microwave heating, global optimisation, heat transfer and polymers.