Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.187 Medellín set-/out. 2014
https://doi.org/10.15446/dyna.v81n186.46103
http://dx.doi.org/10.15446/dyna.v81n187.46103
Heuristic for production scheduling on job-shop plants considering preventive maintenance tasks
Heurística para la secuenciación de producción en plantas job-shop considerando tareas de mantenimiento preventivo
Ronald Díaz-Cazaña a, Yasel José Costa-Salas b & William Ariel Sarache-Castro c
a Facultad de Ingeniería Industrial y Turismo, Universidad Central "Marta Abreu" de Las Villas, Cuba. ronalddc@uclv.edu.cu
b Faculty of Economics, Universidad de Manizales, Colombia. yasel.costa@umanizales.edu.co
c Industrial Engineering Department, Universidad Nacional de Colombia Sede Manizales, Colombia. wasarachec@unal.edu.co
Received: May 28th, 2014.Received in revised form: August 25th, 2014.Accepted: September 10th, 2014
Abstract
The simultaneous analysis of production scheduling and preventive maintenance task attracts special attention of researchers due to its complexity and therefore the necessity to seek efficient methods for solving this kind of combinatorial problems. This paper presents a heuristic approach to solve this issue on job shop plants. The solution method includes a linear programming model, based on the Traveling Salesman Problem, where the setup time is considered as distance measure. The method's aim is to obtain a sequence of production orders and preventive maintenance tasks that reduce the idle time and the backlogs simultaneously, accomplishing the maintenance program. After finding an optimal solution for each machine a Correction Factor (CF) is determined as new distance measure. The CF considers the structure of the initial solution, the machine utilization and the product priorities. Then, the final solution is reached running the linear programming model using the distance updated values. Finally, the proposed heuristic is applied to real case study of the Cuban industry. The experimental results indicated a significant idle time reduction for the company under examination.
Keywords: simultaneous programming; production scheduling; preventive maintenance; linear programming model.
Resumen
El análisis simultáneo de la programación de la producción y las tareas de mantenimiento preventivo atrae especial atención en los investigadores debido a su gran complejidad y por ende la necesidad de encontrar métodos eficientes para resolver este tipo de problema combinatorio. Este artículo presenta un enfoque heurístico para resolver dicha problemática en plantas tipo job-shop. El método de solución incluye un modelo de programación lineal inspirado en el problema del Agente Vendedor, donde el tiempo de iniciación es considerado como métrica de distancia. El método persigue obtener una secuencia de las órdenes de producción y tareas de mantenimiento preventivo que reduzcan el tiempo ocioso y los retrasos simultáneamente, cumpliendo con el programa de mantenimiento. Luego de encontrar la solución óptima para cada máquina, un factor de corrección (CF) es determinado como la nueva medida de distancia. El factor CF considera la estructura inicial de solución, la utilización de las máquinas y las prioridades en los productos. De esta forma, la solución final es alcanzada solucionando el modelo de programación lineal usando los valores de distancia actualizados. Finalmente, la heurística propuesta es aplicada en un caso de estudio real de la Industria Cubana. Los resultados experimentales indicaron una reducción significativa del tiempo ocioso para la compañía objeto de estudio.
Palabras clave: programación simultánea; secuenciación de producción; mantenimiento preventivo; programación lineal.
1. Introduction
One of the elements for optimization, while establishing the manufacturing sequence, is the setup time reduction, due to its influence on equipment downtime. This topic has received a great deal of attention by several current researchers, since great savings are achieved when the setup times are included in the scheduling decisions [1]. In this context, the maintenance tasks programming are inserted, as well as the search for options which allow to generate production-maintenance integrated plans on this level [l-6].
According to [1] most of the researches considering setup times are aimed to flow shop scheduling, while job shop scheduling had been less studied. In the latter case, we stand out the researches carried out by [7] who proposed a heuristic method to minimize the makespan. Authors in [8] tackled this type of problem, in job shop scheduling, through a mixed integer linear programming, developing a heuristic method for its solution, having likewise as an objective, to minimize the makespan. In [9] this is approached considering features such as: release dates, due dates and transportation times. Also [10] developed a hybrid algorithm based on Genetic Algorithms (GAs) which prioritizes the orders according to the shorter processing time dispatching rule; the first operations for every machine are defined from GA, whereas the remaining operations are programmed through the referred dispatching rule, having as an objective the makespan minimization. Similar to the former evolutionary strategy, [11] proposes an elitist GA, which provides a Pareto solution set minimizing simultaneously the makespan and maintenance total cost.
On the other hand, [1] carried out a study applying four metaheuristics to solve a set of instances from the general scheduling problem (including preventive maintenance tasks), considering the machines setup time. Three preventive maintenance (PM) policies were taken into account: 1) PMat fixed predefined time intervals; 2) PM optimum period model, maximizing the machines' availability; 3) maintaining a minimum reliability threshold for a given period. This policies were included in the hybrid metaheuristics: GA-Shorter Processing Time Dispatching Rule (GA-SPT), Simulated Annealing (SA) -Shorter Processing Time Dispatching Rule (SA-SPT), GA adapted for production scheduling and preventive maintenance task simultaneously, from the one proposed by [10] (GA-Ch), and the Immune Algorithm (IA) introduced by [12] for job shop scheduling considering setup times (IA-YZ). After a performance analysis it was concluded that among the metaheuristics, the hybrid method GA-SPT gave the best results and there were no significant differences between the results obtained through SA-SPT and GA-Ch methods; in addition, the IA-YZ showed less solution quality and with the application of the dispatching rule SPT, separately, the worse result was obtained.
Despite the great amount of techniques developed for solving the production scheduling and preventive maintenance problem, including the exact methods [4], heuristics [5] and metaheuristics [13], it cannot be stated that an optimal option for its treatment has been found due to the disadvantages of all of these approximate proposals; for instance, the fact that being so sophisticated, great efforts for its codification and implementation are needed. In other cases the proposals developed lack generality. Many of these methods have specific characteristics, which are rarely applicable to extensions from the original problem.
The latter arguments demonstrate the complexity of the production scheduling and preventive maintenance task problem, considering one or several machines. Furthermore, there exist other real-life characteristics from corporate practice context that raising this complexity when taken into account. Underestimated the aforementioned elements may lead to design models which can give an inappropriate representation of the real problem and, therefore, the solutions would be quite ineffective.
Considering the above, in this paper a heuristic algorithm is proposed, which is aimed to obtain the effective production scheduling and preventive maintenance task in job shop process, minimizing the equipment downtime as a result from the setup time reduction, and thus, facilitating the accomplishment of products delivery due date, having as a premise the compliance of the established preventive maintenance program.
This paper is structured as follows: Section 2 is dedicated to the description of the optimization problem, considering specifically, the integration of the production order scheduling and the preventive maintenance tasks. It is also presented in this section, the mathematical formulation of the problem, as well as a detailed explanation of the steps for the proposed algorithm. In Section 3 the main experimental results from the application of the heuristic algorithm are presented. Afterwards, a discussion about the achieved results is addressed in Section 4. Finally, some conclusions of this research are presented in Section 5.
2. Problem formulation and algorithmic proposal
2.1. Description of the problem
The production environment is characterized by a set 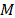 machines and
machines and 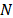 types of products. The manufacturing for each product requires its processing in all or some of the machines, according to its technological sequence. According to the delivery due date, the company defines the priority of each product. The processing time and the setup times for the machines are known. The time for the preventive maintenance task for each machine is known according to the maintenance program.
types of products. The manufacturing for each product requires its processing in all or some of the machines, according to its technological sequence. According to the delivery due date, the company defines the priority of each product. The processing time and the setup times for the machines are known. The time for the preventive maintenance task for each machine is known according to the maintenance program.
Correspondingly to the established manufacturing strategy in the company, the planning objectives in this level are aimed to achieve an optimal exploitation of the production capacity, as well as complying with the delivery due dates. These two decisions can be formulated according to the criteria of minimizing the machines setup time and, simultaneously, minimizing the delivery backlogs.
Thus, the proposed problem consists on establishing the production order sequence (batches of each type of product) and preventive maintenance task on every machine, which minimizes their setup time, accomplishing the product delivery dates and the preventive maintenance program established for each machine.
As a model premise, should be considered that: the manufacturing for a product batch must be not started if its execution time overcomes the remaining time to start the preventive maintenance task. Production interruptions are not acceptable once a batch processing has started, except for failures.
2.2. Heuristic algorithm proposed
The heuristic algorithm proposed in this paper consists of four general steps, which are described below:
Step 1.Initial solution search
It refers to the search of an initial sequence for jobs processing (product batches), independently, on each machines. This initial sequence will minimize the setup time and backlogs. Then, the algorithm is as follows:
For each machine
do:
P1.1Initialize
(Initial number of products)
P1.2 Implement the model as follows:
Parameters:
: Number of products (production orders) to be scheduled.
: Index referring to products.
: Index referring to preventive maintenance task.
: Total orders to be scheduled in the machine, including production and preventive maintenance task.
: Machine setup time between ending order
and beginning order
.
: Machine setup time between ending order
and beginning preventive maintenance task.
: Processing time of order
.
: Priority of order
.
: Priority of order
.
: Priority of order
.
: Time between preventive maintenance tasks.
:
-th component of the subcircuit or analyzed circuit.
: Length of a subcircuit or circuit.
Decision Variables:
: Binary variable, which indicates if the order
is processed {1} or not {0} after the order
.
: Binary variable, which indicates if the preventive maintenance task
will be scheduled {1} or not {0} in the sequence after the order
.
: Binary variable, which indicates if the order k will be the first {1} or not {0} in the production sequence.
: Slack variable.
Objective function:
To reduce the setup time (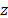 ) in the equipment,
) in the equipment,
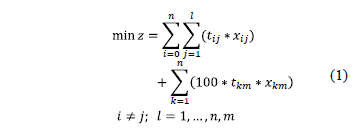
It was used the constant value of 100 in order to ensure that the model sequences the major quantity of orders until the moment for the preventive maintenance task occurs. This value was defined after some a priori values previously tested.
Constraints:
1) To ensure the accomplishment for the preventive maintenance program,
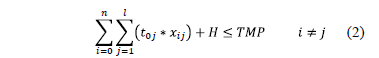
2) To ensure that one order can be preceded by one order only,
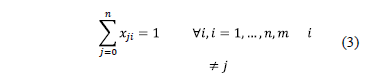
3) To ensure that from a node only comes out one arc (i.e. an order can be preceded by one order only),
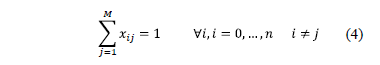
4) To avoid subcircuits and circuit. Specifically for all of the long subcircuits  ,
,  and circuit,
and circuit,
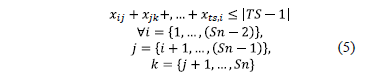
5) To ensure a logical sequence,
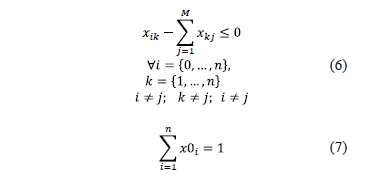
If 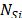 is lower than the number of products
is lower than the number of products 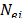 to be manufactured in the machine
to be manufactured in the machine 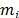 , repeat step P1.2 with the remaining products for sequencing; otherwise go to Step 2.
, repeat step P1.2 with the remaining products for sequencing; otherwise go to Step 2.
Step 2. Obtaining the relative importance for every machine
The relative importance (weight) for every machine can be computed based on various criteria. One of them, which is the one adopted in this paper, is the capacity utilization rate, which aims to favor the most loaded machines in the obtained final sequence. For the weight determination, any of the qualitative or quantitative current methods can be applied.
Step 3. Obtaining a corrected distance measure
With this new measure, it is attempted to correct the initial distance measure adopted in Step 1. To obtain it, a coefficient 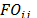 is proposed (order factor for product
is proposed (order factor for product 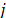 with respect to machine
with respect to machine 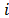 . This coefficient integrates three factors:
. This coefficient integrates three factors:
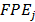 : Priority factor for product
: Priority factor for product 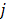 based on its delivery date. This factor is calculated only once for each product, regardless the machines.
based on its delivery date. This factor is calculated only once for each product, regardless the machines.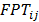 : Technological priority factor for product
: Technological priority factor for product 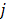 with respect to the machine
with respect to the machine 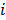 . It constitutes a proximity measure between the position of product
. It constitutes a proximity measure between the position of product 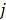 , according to the initial sequence, with respect to the machine
, according to the initial sequence, with respect to the machine 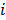 , and the weighted position of the product considering all the machines, also based on the initial sequence. This factor is calculated only once, for each product depending on every machine, using the information supplied by the initial sequence of every machine.
, and the weighted position of the product considering all the machines, also based on the initial sequence. This factor is calculated only once, for each product depending on every machine, using the information supplied by the initial sequence of every machine. 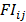 : Starting factor for product
: Starting factor for product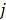 with respect to the machine
with respect to the machine 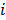 . It is a measure for the availability of the product
. It is a measure for the availability of the product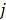 , in a specific moment, to start its processing in a machine
, in a specific moment, to start its processing in a machine 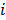 after being processed in the machine
after being processed in the machine 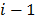 according to its operation sequence. The starting factor must be calculated for every machine as the machine is going to be sequenced. This factor ranges from
according to its operation sequence. The starting factor must be calculated for every machine as the machine is going to be sequenced. This factor ranges from 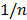 to
to 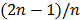 .
.
The proposed mathematical expressions to calculate these factors and the corrected distance are the following:
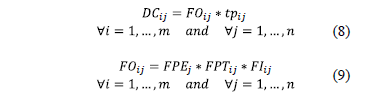
If it is assigned 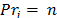 to the product with the highest priority,
to the product with the highest priority,
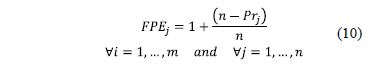
If it is assigned 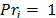 to the product with the highest priority,
to the product with the highest priority,
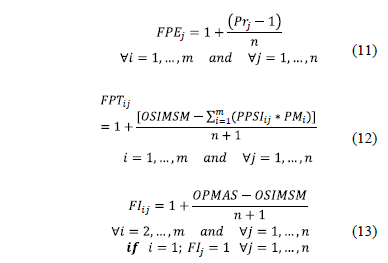
where:
: Corrected distance for the product
used for obtaining the final sequencing with respect to the machine
.
: Order factor for product
with respect to machine
.
: Setup time in the machine when product
is changed for product
according to the initial sequence.
: Position for product
according to the initial sequence of the machine
.
: Weight for the machine
.
: Number of products to be manufactured.
: Number of machines
: Priority order given to the product
according to its delivery date.
.
: Order in which the product would be processed in the previously sequenced machine to the one that is being sequenced at the present moment, according to the initial sequence.
: Order of the product in the initial sequence for the machine that is being sequenced at the present moment.
Step 4. Obtaining the final solution
For every machine
do:
P4.1 Initialize
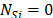
P4.2 Implement the proposed mathematical model in P1.2, but taking into account as a distance measure the corrected distances ().
If 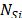 is lower than the number of products
is lower than the number of products 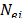 (products to be manufactured in the machine
(products to be manufactured in the machine 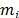 ) repeat P4.2 with the remaining products for sequencing; otherwise take the solution obtained for every machine as a final integrated sequence for production orders and preventive maintenance.
) repeat P4.2 with the remaining products for sequencing; otherwise take the solution obtained for every machine as a final integrated sequence for production orders and preventive maintenance.
3. Experimental results
Step 1. Implementation: Searching for an initial solution
The production environment is characterized by a set of five machines (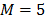 ): mechanical saw (
): mechanical saw (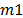 ), conventional lathe (
), conventional lathe (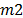 ), milling machine (
), milling machine (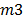 ), grinding machine (
), grinding machine (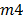 ), sharpening machine (
), sharpening machine (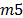 ); and a set N of six (6) types of products: punches (
); and a set N of six (6) types of products: punches (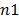 ), matrix (
), matrix (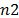 ), dies (
), dies ( ), pintles (
), pintles ( ), blades (
), blades ( ) and nozzles (
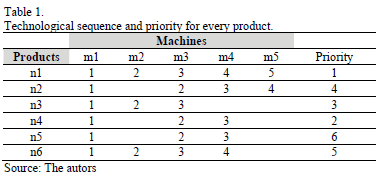
) and nozzles ( ). The processing sequence and priority for every product is shown in Table 1.
). The processing sequence and priority for every product is shown in Table 1.
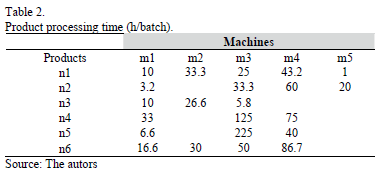
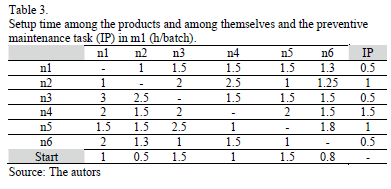
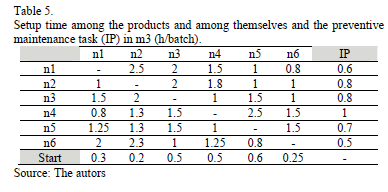
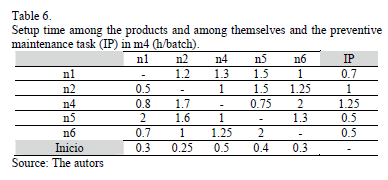
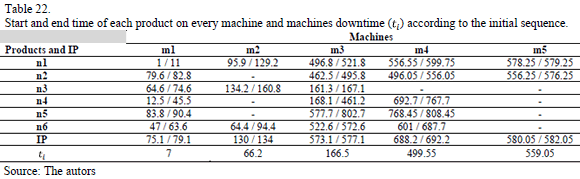
Table 2 contains the processing time of each product on every machine; whereas Tables 3, 4, 5, 6 y 7 show the setup time of every machine to change from one product to another, as well as the time between orders and preventive maintenance task.
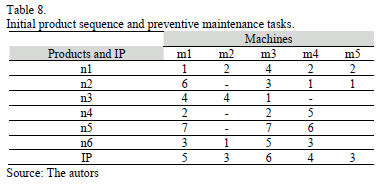
The preventive maintenance task, in every one of the five machines taken into account, must be done every 72, 72, 240, 192 y 24 operating hours, respectively. The initial sequence of production orders and preventive maintenance task (IP) for each one of the 5 machines is showed in Table 8.
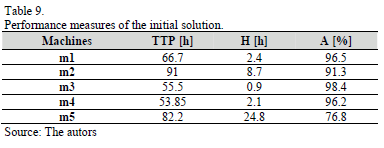
In Table 9 are presented possible performance measures for each one of the machines, based on the initial sequence obtained: the total setup time (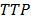 ),the idle time while waiting for the moment to start the maintenance task, given by the slack variable (
),the idle time while waiting for the moment to start the maintenance task, given by the slack variable (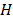 ) used in the mathematical model and, the corresponding capacity utilization rate (
) used in the mathematical model and, the corresponding capacity utilization rate (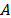 ),resulting from the latter measure (idle time).
),resulting from the latter measure (idle time).
Once all products in every machine have been sequenced, the Step 2 is applied.
Step 2. Implementation: Obtaining the relative importance of every machine
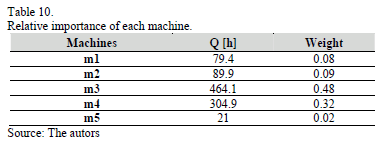
The relative importance (weight) of each machine is established according to its workload (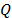 ) expressed in hours, so the most loaded machines obtain more weight. The results are shown in Table 10.
) expressed in hours, so the most loaded machines obtain more weight. The results are shown in Table 10.
Step 3. Implementation: Obtaining the corrected distance for each product on every machine
In Table 11 is presented priority factor for product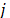 based on its delivery date (
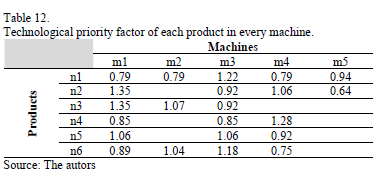
based on its delivery date (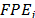 ). Then, in Table 12, is shown technological priority factor for product
). Then, in Table 12, is shown technological priority factor for product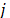 with respect to the machine
with respect to the machine 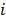 (
(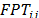 ).
).
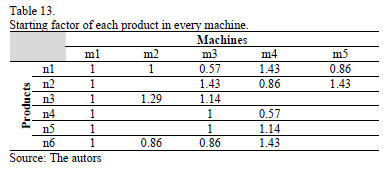
In Table 13 is shown the starting factor for product 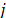 with respect to the machine
with respect to the machine 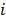 (
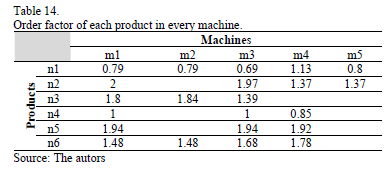
(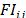 ). Thereafter, in Table 14, is shown the order factor for product
). Thereafter, in Table 14, is shown the order factor for product 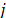 with respect to machine
with respect to machine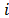 (
(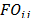 ).
).
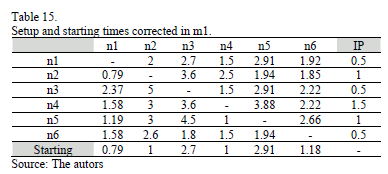
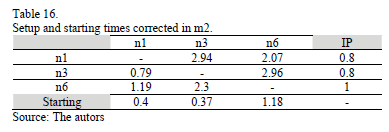
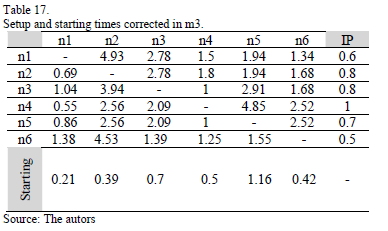
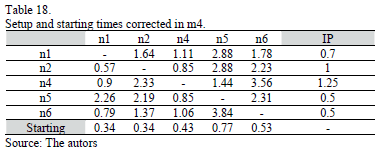
In Tables 15, 16, 17, 18 and 19 are shown the corrected representative distance measures of the setup times in each machine (in hours).
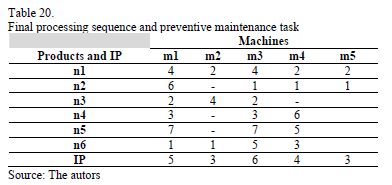
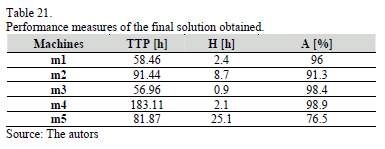
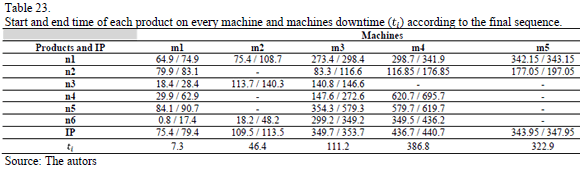
In Table 20 the final processing sequence and preventive maintenance tasks for every machine is shown. In Table 21 are shown the performance measures previously described.
In Tables 22 and 23 it is shown the moment where each product begins its processing in each one of the machines and the corresponding downtime of each one of these machines, obtained from the initial and final sequence, respectively. Considering that the processing starts at zero time and there are no other products in process, the initial solution reported a total downtime of 1298.3 hours.
According to Table 23 the total downtime is 874.6 hours. Therefore, the proposed heuristics achieves a reduction of 423.7 hours respecting to the initial solution, which corresponds to the generation of local optimum solutions in each one of the machines. The expression (14) allows quantifying the total weighted disruption time, based on the fact that one of the defined objectives is to achieve the maximum equipment utilization, giving a major priority to the most loaded machines.
Replacing the results of the initial solution in the expression (14), a total weighted disruption time of 257.5 h. is obtained. This performance measure, according to the final solution provided by the proposed method is reduced to188.4 h.

where:
: Total weighted downtime.
: Downtime of machine
.
: Weight of the machine
according to its utilization level (Table 10).
4. Discussion
Despite that the proposed method does not consider many of the situations that can occur when the production scheduling and preventive maintenance tasks are undertaken in an integrated manner, such as random failure events and their impact on manufacturing technology and even on the maintenance and production program obtained, a scheduling horizon definition which covers more than one preventive maintenance task, among others, is considered an efficient tool for scheduling within the treated study, being its extension possible to productive contexts with similar characteristics, where the machine setup time takes the significant values within the shift work. It is important to establish the objectives to the scheduling process, and the priority to achieve them, as one of the basic heuristic inputs, since the structure of the final solution obtained will depend greatly on it.
In the examined case study, since it was more important for the decision maker to minimize the downtime than complying with the delivery dates, it can be observed how the major priority products (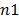 y
y 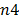 ) are not the first to be completed, which could be interpreted as an inconsistency in the proposed method; however, this result responds to the hierarchical structure which takes the branch and bound method used to solve the linear integer programming model. For subsequent papers it will be interesting to consider the variations that could be obtained in the solution structure if only one objective function was applied in the mathematical model, which could integrate the objectives that are expected to be optimized, assigning them different weights in the equation in order to model the hierarchical importance that the decision maker adopts for them, besides considering the possibility of assigning different weights to the components which conform the order factors used to obtain the corrected distance measure.
) are not the first to be completed, which could be interpreted as an inconsistency in the proposed method; however, this result responds to the hierarchical structure which takes the branch and bound method used to solve the linear integer programming model. For subsequent papers it will be interesting to consider the variations that could be obtained in the solution structure if only one objective function was applied in the mathematical model, which could integrate the objectives that are expected to be optimized, assigning them different weights in the equation in order to model the hierarchical importance that the decision maker adopts for them, besides considering the possibility of assigning different weights to the components which conform the order factors used to obtain the corrected distance measure.
5. Conclusions
In the literature, several proposals can be found focused on obtaining production order sequences and preventive maintenance tasks in an integrated manner, which include mathematical models and proper heuristic methods from the field of Artificial Intelligence, due to the complexity that this type of problem entails; however, it cannot be stated that an optimal option for its treatment has been found due to the disadvantages of all of these proposals, for instance, the fact that being so sophisticated, great efforts for its codification and implementation are needed and, in other cases, many of these methods have specific characteristics which are rarely applicable to branches from the origin problem.
The heuristic method proposed in this paper allows obtaining the optimal processing sequence and preventive maintenance tasks, so the equipment setup time is minimized and the downtime as well, contributing to achieve the delivery dates compliance for the products and the maintenance plan previously established is kept. It includes the design of a mathematical model based on the general scheme of the model used in the Traveling Salesman Problem, setting up certain constraints to consider the time between preventive maintenance tasks on the machines, besides avoiding circuits, which would conform an incoherent solution for the tackled problem.
The validation of the proposed method was carried out from its application in a productive context characterized by five machines and six types of products, considering a preventive maintenance task for every machine. This solution reported a reduction of 423.7 hours in the total downtime.
References
[1] Naderi, B., Zandieh, M. and Fatemi-Ghomi, S., A study on integrating sequence dependent setup time flexible flow lines and preventive maintenance scheduling, Journal of Intelligent Manufacturing, 20 (6), pp. 683-694, 2009. [ Links ]
[2] Low, C., Ji, M., Hsu, C-J. and Su, C-T., Minimizing the makespan in a single machine scheduling problems with flexible and periodic maintenance, Applied Mathematical Modelling, 34 (2), pp. 334-342, 2010. [ Links ]
[3] Xu, D., Sun, K. and Li, H., Parallel machine scheduling with almost periodic maintenance and non-preemptive jobs to minimize makespan, Computers & Operations Research, 35 (4), pp. 1344-1349, 2008. [ Links ]
[4] Wang, S. and Liu, M., A branch and bound algorithm for single-machine production scheduling integrated with preventive maintenance planning, International Journal of Production Research, 51 (3), pp. 847-868, 2012. [ Links ]
[5] Alaoui-Selsouli, M., Mohafid, A. and Najid, N.M., Lagrangian relaxation based heuristic for an integrated production and maintenance planning problem, International Journal of Production Research, 50(13), pp. 3630-3642, 2012. [ Links ]
[6] Machani, M. and Nourelfath, M., A variable neighborhood search for integrated production and preventive maintenance planning in multi-state systems, International Journal of Production Research, 50 (13), pp. 3643-3660, 2012. [ Links ]
[7] Chen, Z. and Egbelu, P.J., Scheduling in a manufacturing shop with sequence-dependent setups, Robotics and Computer-Integrated Manufacturing, 5 (1), pp. 73-81, 1989. [ Links ]
[8] Choi, I. and Korkmaz, O., Job shop scheduling with separable sequence-dependent setups, Annals Operational Research, 70 (0), pp. 155-170, 1997. [ Links ]
[9] Schutten, J., Practical job shop scheduling, Annals Operational Research, 83 (0), pp. 161-178, 1998. [ Links ]
[10] Cheung, W. and Zhou, H., Using genetic algorithms and heuristics for job shop scheduling with sequence-dependent setup times, Annals Operational Research, 107 (1-4), pp. 65-81, 2001. [ Links ]
[11] Ben-Ali, M., Sassi, M., Gossa, M. and Harrath, Y., Simultaneous scheduling of production and maintenance tasks in the job shop, International Journal of Production Research, 49 (13), pp. 3891-3918. [ Links ]
[12] Zhou, Y., Beizhi, L. and Jianguo, Y., Study on job shop scheduling with sequence-dependent setup times using biological immune algorithm, The International Journal of Advanced Manufacturing Technology, 30 (1-2), pp. 105-111, 2006. [ Links ]
[13] Wong, C.S., Chan, F.T.S. and Chung, S.H., A joint production scheduling approach considering multiple resources and preventive maintenance tasks, International Journal of Production Research, 51 (3), pp. 883-896, 2012. [ Links ]
R. Díaz-Cazaña, is an Industrial Engineer from the Universidad Central "Marta Abreu" de Las Villas, Cuba. He obtained the MSc. in 2008 in the aforementioned University. Production research, maintenance planning and human force planning highlighted within his main research areas. He works as Associate Professor in the Department of Industrial Engineering in the Universidad Central "Marta Abreu" de Las Villas, Cuba.
Y. J. Costa-Salas, is an Industrial Engineer from the Universidad Central "Marta Abreu" de Las Villas, Cuba. He received the Dr. in Engieneer in the prestigious German Institution Otto-von-Guericke University. His research interests cover several topics of Applied Mathematics in decision making: mathematical programming and approximate algorithms for hard combinatorial problems, bio-inspired algorithms, and supply chain optimization, among others. Prof. Costa belongs to the referee staff of many well-known international journals such as European Journal of Operational Research, Expert System with Application and Decision Science. He works as Associate Professor in the Faculty of Economics at Universidad de Manizales, Colombia.
W.A. Sarache-Castro, obtained his Industrial Engineer degree from the Universidad de Ibagué, Colombia. He received the PhD in the Universidad Central "Marta Abreu" de Las Villas, Cuba. His has many contributions in the research field of Logistics and Operation Management. His is Associate Professor of the Industrial Engineering Department at Universidad Nacional de Colombia, Sede Manizales, Colombia.