Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.191 Medellín May/June 2015
https://doi.org/10.15446/dyna.v82n191.51140
DOI: http://dx.doi.org/10.15446/dyna.v82n191.51140
A new synthesis procedure for TOPSIS based on AHP
Un nuevo procedimiento de síntesis para TOPSIS basado en AHP
Juan Aguarón-Joven a; María Teresa Escobar-Urmeneta b; Jorge Luis García-Alcaraz c; José María Moreno-Jiménez d * & Alberto Vega-Bonilla e
a Zaragoza Multicriteria Decision Making Group, Faculty of Economics and Business, University of Zaragoza. Spain. aguaron@unizar.es
b Zaragoza Multicriteria Decision Making Group, Faculty of Economics and Business, University of Zaragoza. Spain. mescobar@unizar.es
c Department of Industrial Engineering and Manufacturing, Autonomous University of Ciudad Juarez, Ciudad Juárez México. jorge.garcia@uacj.mx
d Zaragoza Multicriteria Decision Making Group, Faculty of Economics and Business, University of Zaragoza. Spain. moreno@unizar.es
e Department of Industrial Engineering and Manufacturing, Autonomous University of Ciudad Juarez, Ciudad Juárez México. albertovega18@gmail.com
Received: January 28th, 2015. Received in revised form: March 26th, 2015. Accepted: April 30th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
Vega et al. [1] analyzed the influence of the attributes' dependence when ranking a set of alternatives in a multicriteria decision making problem with TOPSIS. They also proposed the use of the Mahalanobis distance to incorporate the correlations among the attributes in TOPSIS. Even in those situations for which dependence among attributes is very slight, the results obtained for the Mahalanobis distance are significantly different from those obtained with the Euclidean distance, traditionally used in TOPSIS, and also from results obtained using any other distance of the Minkowsky family. This raises serious doubts regarding the selection of the distance that should be employed in each case. To deal with the problem of the attributes' dependence and the question of the selection of the most appropriate distance measure, this paper proposes to use a new method for synthesizing the distances to the ideal and the anti-ideal in TOPSIS. The new procedure is based on the Analytic Hierarchy Process and is able to capture the relative importance of both distances in the context given by the measure that is considered; it also provides rankings, which are closer to the distances employed in TOPSIS, regardless of the dependence among the attributes. The new technique has been applied to the illustrative example employed in Vega et al. [1].
Keywords: Multicriteria Decision Making, TOPSIS, AHP, Dependence, Synthesis.
Resumen
Vega et al. [1] analizan la influencia que tiene la dependencia entre atributos al ordenar con TOPSIS un conjunto de alternativas en un problema de decisión multicriterio. Asimismo, estos autores proponen utilizar la distancia de Mahalanobis en TOPSIS para incorporar las correlaciones entre los atributos. El problema es que, incluso en situaciones en las que la dependencia entre atributos es muy pequeña, los resultados obtenidos utilizando la distancia de Mahalanobis difieren significativamente de los obtenidos con la distancia euclídea tradicionalmente empleada en TOPSIS, así como de los obtenidos con cualquier otra distancia de la familia de Minkowsky. Este hecho provoca serias dudas a la hora de seleccionar la distancia que debe utilizarse en cada caso. Para abordar el problema de la dependencia entre atributos y el asociado con la selección de la distancia más apropiada, este trabajo propone utilizar una nueva forma de sintetizar las distancias al ideal y anti-ideal en TOPSIS. Este nuevo procedimiento, basado en el Proceso Analítico Jerárquico (AHP), permite capturar la importancia relativa de ambas distancias en el contexto delimitado por la medida considerada y proporciona ordenaciones más cercanas que las de la síntesis tradicional para las diferentes distancias empleadas con TOPSIS, independientemente de la existencia de dependencia entre atributos. El procedimiento propuesto ha sido aplicado al ejemplo seleccionado por Vega et al. [1].
Palabras clave: Decisión Multicriterio, TOPSIS, AHP, Dependencia, Síntesis.
1. Introduction
TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) is a multicriteria decision making technique used for ranking and selecting the best alternative from a discrete group (Ai, i=1,
,m) [2,3]. This technique is based on the minimization of geometric distances from the alternatives to the ideal (A+) and anti-ideal (A-) solutions. In order to calculate the relative proximity (Ri) from Ai to A+ and A-, traditional TOPSIS [2] uses the Euclidean distance, which implicitly assumes that the attributes contemplated for ordering alternatives are independent, and an indicator, or proximity index (Ri), which synthesizes (see Section 2.1.3) the information of both distances as a ratio (Ri=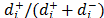 ).
).
Unfortunately, independence of attributes rarely occurs in the real-life cases to which the technique is applied [4]. Moreover, its study is especially complex and difficult. After analyzing the relevance of this topic, Vega et al. [1] adapted TOPSIS to the consideration of dependent attributes by means of the reformulation of Hwang and Yoon's initial proposal [3].
The modification comprised a new measurement of ideal and anti-ideal distances, based on the Mahalanobis distance [5, 6], which captures the correlation between the attributes [7] and eliminates the common problem of data normalization. This reformulation provides very different results to those obtained with the Euclidean distance even if the dependence among the attributes is very slight [1].
To deal with this conflicting point, this paper proposes a new method, based on the Analytic Hierarchy Process (AHP), for synthesizing the contribution of the two distances (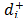 and
and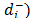 to the final ordering. The new synthesizing procedure allows the consideration of both aspects of different relative importance and without the difficulties associated with a quotient. The new relative importance index (Wi) for each alternative (see Section 3 for details), obtained as Wi = w+ w(
to the final ordering. The new synthesizing procedure allows the consideration of both aspects of different relative importance and without the difficulties associated with a quotient. The new relative importance index (Wi) for each alternative (see Section 3 for details), obtained as Wi = w+ w(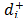 ) + w- w(
) + w- w(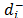 ), reduces the divergence between the rankings that result from the Euclidean and Mahalanobis distances.
), reduces the divergence between the rankings that result from the Euclidean and Mahalanobis distances.
The structure of the remainder of this paper is as follows: Section 2 briefly describes the multicriteria decision making techniques that use the minimization of distances as methodological support; Section 3 includes the proposal of Vega et al. [1] for dealing with the dependence among the attributes; Section 4 presents the new synthesis process, based on the Analytic Hierarchy Process, and proposed for TOPSIS, the section further includes an illustrative example; finally, Section 5 briefly details the most important conclusions of the work.
2. Background
2.1. Multicriteria decision making techniques based on minimization distances
Multicriteria Decision Making can be understood as a series of models, methods and techniques that allow a more effective and realistic solution to complex problems that contemplate multiple scenarios, actors and (tangible and intangible) criteria [8,9]. A variety of multicriteria decision approaches are mentioned in the scientific literature [10].
Despite the diversity of the techniques and the many arguments and discussions that have taken place regarding the different schools and approaches, there is no general agreement that a particular technique is superior to the others [11]. Moreover, in the last decade, debates between the different schools have been replaced by attempts to take advantage of the best elements of each approach in order to develop the most effective technique.
With respect to the multicriteria techniques based on distance minimization, the original and most commonly used is Compromise Programming [10,12-13]. This technique, with a priori information about the decision maker's preferences (norms and weights), simultaneously works with all the criteria and seeks a solution that minimizes the distance to the ideal point.
Let (1) be a multi-objective optimization problem where, without losing generality, it is supposed that all the q contemplated criteria are maximized:
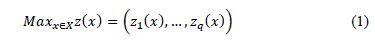
The compromise solution is obtained by resolving the optimization problem that minimizes the distance to the ideal point or vector 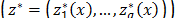 , where that distance is usually given by a Minkowski distance expression:
, where that distance is usually given by a Minkowski distance expression:
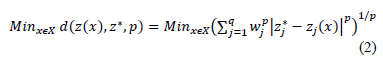
Given that 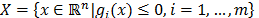 and
and 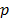 is the norm considered for distance
is the norm considered for distance 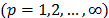 ,
, 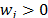 is the weight of
is the weight of 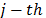 criterion and
criterion and 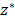 is the ideal vector where each component
is the ideal vector where each component 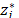 of the vector is the individualised optimum of the
of the vector is the individualised optimum of the 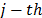 criteria
criteria 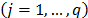 , we have:
, we have:

When 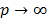 , the expression of the Minkowski distance is known as the Tchebycheff distance; in this case (2) it is:
, the expression of the Minkowski distance is known as the Tchebycheff distance; in this case (2) it is:
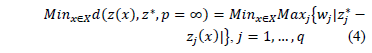
For reasons of operational functionality, the most commonly used Minkowski norms are: 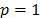 (Manhattan distance),
(Manhattan distance), 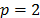 (Euclidean distance) and
(Euclidean distance) and 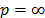 (Tchebycheff distance). In the first case, the optimization problem is linear, in the second it is quadratic and in the third case, the model can be easily transformed into a linear one.
(Tchebycheff distance). In the first case, the optimization problem is linear, in the second it is quadratic and in the third case, the model can be easily transformed into a linear one.
Other well-known multicriteria techniques based on the minimization of distances that have been widely used in discrete multicriteria decision-making are: Goal Programming [14], VIKOR [15] and TOPSIS.
2.1.1. Goal programming (GP)
GP is a multicriteria technique that uses the distance minimization concept, but is more focused on the concept of satisfaction, moving away from the traditional concept of optimization. GP integrates a set of constrains that represent some resource limitations or capacities, and can be represented according to (5):
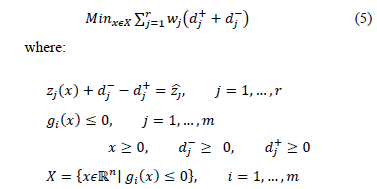
2.1.2. VIKOR technique
VIKOR (VIseKriterijumska Optimizacija I Kompromisno Resenje in Serbian) was originally proposed by Serafim Opricovic in his Ph. D. dissertation (1979) aimed at resolving complex decision problems with conflicting and non-commensurable criteria [15]. For the ranking of the alternatives and the selection of the best one, it uses an index that measures the proximity to the ideal solution. The distance employed for measuring the proximity belongs to the Lp-Minkowsky metric that is traditionally used in Compromise programing [12-13].
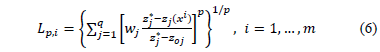
When seeking the integration of all the attributes in the ranking process, it is necessary to express them in dimensionless scales. The normalization mode used by VIKOR is utility normalization:
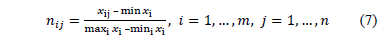
With dimensionless measures, the next step is to estimate the measurement of satisfaction 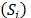 and regret (Ri):
and regret (Ri):
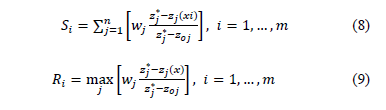
Using these values, VIKOR estimates a proximity index for every alternative:
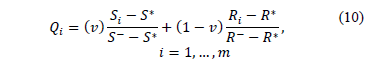
where:  = Mini
= Mini ,
,  = Maxi
= Maxi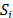 ,
, 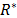 = Mini
= Mini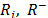 = Maxi
= Maxi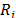 and
and 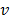 is the weight associated with the normalised difference from the best collective strategy (best solution with p=1) and
is the weight associated with the normalised difference from the best collective strategy (best solution with p=1) and 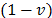 the weight associated with the normalised difference to the best individual rejection strategy (best solution with p=¥).
the weight associated with the normalised difference to the best individual rejection strategy (best solution with p=¥).
These weights take values in a range between 0 and 1. For example, for 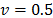 indicates consensus among decision makers. If
indicates consensus among decision makers. If 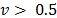 then majority have more weight in the decision process. But if
then majority have more weight in the decision process. But if 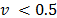 , the minority have more weight, producing a veto effect. The results for
, the minority have more weight, producing a veto effect. The results for 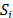 ,
, 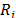 and
and 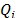 are three lists that allow the alternatives to be ranked in descending order.
are three lists that allow the alternatives to be ranked in descending order.
2.1.3. Traditional TOPSIS technique (TOPSIS-T)
Given a discrete multicriteria decision problem with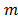 alternatives
alternatives 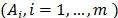 evaluated with respect to
evaluated with respect to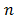 criteria
criteria 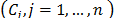 , each element
, each element 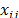 in Table 1 represents the value associated with alternative
in Table 1 represents the value associated with alternative 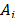 for the attribute or criterion
for the attribute or criterion 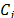 , of which the weight or importance is
, of which the weight or importance is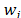 . Traditional TOPSIS (TOPSIS-T) contemplates each alternative or object as a point or vector of an-dimensional space (see decision matrix in Table 1).
. Traditional TOPSIS (TOPSIS-T) contemplates each alternative or object as a point or vector of an-dimensional space (see decision matrix in Table 1).
TOPSIS-T calculates the Euclidean distance between the normalized values (with the distributive mode) of the initial alternatives 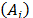 and those of two special alternatives: the ideal
and those of two special alternatives: the ideal 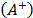 and the anti-ideal
and the anti-ideal 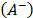 , on the understanding that the best alternatives are those which are closer to the ideal and further away from the anti-ideal. To apply this technique, the attributes' values should be numerical and have commensurable units.
, on the understanding that the best alternatives are those which are closer to the ideal and further away from the anti-ideal. To apply this technique, the attributes' values should be numerical and have commensurable units.
TOPSIS implicitly assumes that the contemplated attributes are independent [16,17]. Unfortunately, this rarely occurs in the real-life cases where the technique is applied. The procedure is better described in the following steps, as suggested by Hwang and Yoon [3] in their original proposal (traditional TOPSIS):
Step 1. Calculate the normalized decision matrix
As TOPSIS allows the evaluated criteria to be expressed in different measurement units, it is necessary to convert them into normalized values. The normalization process, like the metric used to calculate the ideal and anti-ideal distances, is the Euclidean one.
In this case, the normalization of element 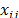 of the decision matrix (Euclidean normalisation mode,
of the decision matrix (Euclidean normalisation mode, 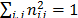 ) is calculated as:
) is calculated as:
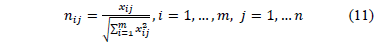
Step 2. Calculate the weighted normalized decision matrix
The weighted normalized value 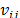 is calculated as:
is calculated as:
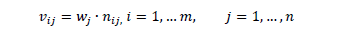
with 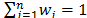 . The weights
. The weights 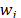 can be obtained by means of different procedures [10]: direct assignation, AHP, etc.
can be obtained by means of different procedures [10]: direct assignation, AHP, etc.
Step 3. Determine the "positive ideal" and "negative ideal" alternatives
Without losing generality and supposing that all the criteria are maximized, the ideal positive solution is given by 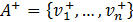 , where
, where 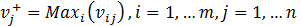 , and the ideal negative or anti-ideal solution is given by
, and the ideal negative or anti-ideal solution is given by 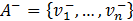 where
where 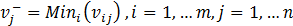 .
.
Step 4. Calculate the distances
The separation of each alternative 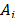 from the ideal solution
from the ideal solution 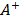 is calculated as
is calculated as 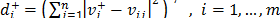 . In a similar way, the separation of each alternative
. In a similar way, the separation of each alternative 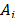 from the ant-ideal solution
from the ant-ideal solution 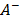 is calculated as
is calculated as 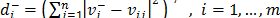 .
.
Step 5. Calculate the relative proximity to the ideal solution
The relative proximity from 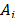 to
to 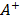 and
and 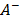 is given by:
is given by:
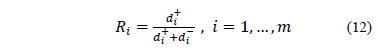
where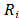 is named the proximity index and low values are better.
is named the proximity index and low values are better.
Step 6. Preference order
Finally, 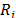 is used to rank the alternatives; the nearest the value of the proximity index
is used to rank the alternatives; the nearest the value of the proximity index 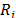 is to 0, the greater its proximity to the ideal, the higher its priority. In short, (Ai>Aj Û Ri<Rj).
is to 0, the greater its proximity to the ideal, the higher its priority. In short, (Ai>Aj Û Ri<Rj).
2.2. The Analytic Hierarchy Process (AHP)
The Analytic Hierarchy Process (AHP) is a multicriteria decision making methodology created by the mathematician Thomas Saaty in the 1970s. It deals with the multicriteria ranking and selection of a discrete set of alternatives in a context with multiple scenarios, actors and criteria (tangible and intangible).
The AHP methodology [18-19] comprises the following stages:
(i) Modeling the problem: the construction of a hierarchy, the identification of the mission, the relevant criteria to its execution, the sub-criteria for each criterion, the actors and the alternatives.
(ii) Valuation: the incorporation of the actors' preferences by means of pairwise comparisons between the elements of the hierarchy that hang from the same node; this process uses judgments from Saaty's fundamental scale (see Table 2) and the result is a square, reciprocal and positive pairwise comparison matrix that reflects the relative importance of two elements with respect to the common element in the higher level of the hierarchy.
(iii) Prioritization and synthesis: the determination of the local and global priorities for the elements of the hierarchy and the total priorities for the alternatives of the problem. Saaty's Eigen Vector method (EGV) and the Row Geometric Mean method (RGM) are the two most common prioritization procedures [18].
One of the characteristics which differentiates this methodology from other multicriteria approaches is that AHP measures the inconsistency of the actors when eliciting the judgments of the pairwise comparison matrices in a formal, elegant and intrinsic manner, linked to the mathematical prioritization procedure. Saaty`s Consistency Ratio (CR) and Aguarón & Moreno-Jiménez's Geometric Consistency Index (GCI) are the two inconsistency measures usually employed with the EGV and the RGM prioritization procedures, respectively [20].
3. Dependent attributes in TOPSIS. TOPSIS-M
It is well known that all multi-attribute techniques may be improved, depending on the theory on which they are based [21,22]. TOPSIS is no exception. One of its main limitations is the correlation between attributes; in other words, this technique assumes that all the attributes are independent and this is not always the case.
There are several ways for measuring the dependence among the attributes [23]. Some of the most widely used are: the scatterplots matrix, the correlation matrix, variance inflation factors, condition numbers [24,25] and the Gleason-Staelin indicator.
The scatterplots matrix is a visual tool that plots each attribute against the other in matrix form; this allows the observation of patterns or linear trends that helps to determine the dependence between attributes. The Correlation matrix, S = (sij), is a square (nxn) symmetrical matrix in which each entry sij is the correlation between attributes i and j (sijÎ[-1,1]). The Variance Inflation Factor (VIF) for the attribute j is given by VIFj= 1/(1-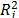 ), where
), where 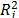 is the coefficient of determination of attribute
is the coefficient of determination of attribute 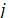 over others in a multiple linear regression. Values of VIF greater than 10 indicate strong dependence in the data [26]. The Condition Numbers are calculated [27] as nj = lmax/ lmin, where lmax and lmin are the maximum and minimum eigen-values of the XTX matrix. If any of the condition numbers calculated for the set of attributes is greater than 1000, it indicates that there is no independence between the attributes. The Gleason-Staelin redundancy measure (Phi) is given by [28]:
over others in a multiple linear regression. Values of VIF greater than 10 indicate strong dependence in the data [26]. The Condition Numbers are calculated [27] as nj = lmax/ lmin, where lmax and lmin are the maximum and minimum eigen-values of the XTX matrix. If any of the condition numbers calculated for the set of attributes is greater than 1000, it indicates that there is no independence between the attributes. The Gleason-Staelin redundancy measure (Phi) is given by [28]:
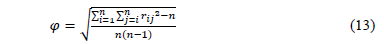
where the rij (i,j=1, ,n) are the correlations between the attributes. If this indicator is higher than 0.5, it is an indication of redundancy and dependence in the data.
To deal with the problem of dependence among the attributes, Vega et al. [1] proposed an extension of TOPSIS-T, named TOPSIS-M, which uses the Mahalanobis distance instead of the Euclidean distance in Step 4 of the previous algorithm.
TOPSIS-M solves two of the limitations of TOPSIS-T: (i) the redundancy provoked by the dependence when measuring the proximity with the Euclidean distance and (ii) the problem of selecting the appropriate mode for normalizing the data. Using the Mahalanobis distance is not necessary to normalize the initial data. The value of the Mahalanobis distance is the same, apart from the used normalization mode that is used. The value is also the same without normalization.
The Mahalanobis distance [5,6] determines the similarity between two multi-dimensional random variables as well as considering the existent correlation between them (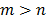 is required to obtain
is required to obtain 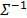 ). The Mahalanobis distance between two random variables with the same
). The Mahalanobis distance between two random variables with the same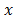 and
and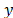 probability distribution and with S variance-covariance matrix is formally defined as:
probability distribution and with S variance-covariance matrix is formally defined as:
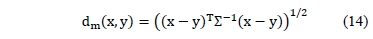
Where
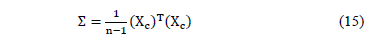
and X is the data matrix with m objects in rows and n columns, 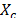 the centered matrix,
the centered matrix,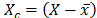 , and
, and 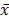 the arithmetic mean.
the arithmetic mean.
This value coincides with the Euclidean distance if the covariance matrix is the identity matrix, i.e. if all bivariate correlations between variables are zero. When there is some dependence among the attributes, even if it is very small (Gleason-Staelin's 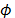 < 0.025), the rankings obtained with the Euclidean distance and those obtained with the Mahalanobis distance can be significantly different [1]. This is also true for the other distances of the Minkowsky family and it is especially notable with the Manhattan (p=1) and the Tchebycheff distances (p=¥) [1].
< 0.025), the rankings obtained with the Euclidean distance and those obtained with the Mahalanobis distance can be significantly different [1]. This is also true for the other distances of the Minkowsky family and it is especially notable with the Manhattan (p=1) and the Tchebycheff distances (p=¥) [1].
In order to deal with this contradiction, in the next section, we advance a new synthesis procedure (Step 5 of the TOPSIS algorithm), based on the Analytic Hierarchy Process (AHP), that allows the consideration of the relative importance of the distances from the ideal and anti-ideal alternatives and provides results that are closer for the distances employed than those obtained with the traditional TOPSIS approach, regardless of the normalization model used.
4. A new synthesis procedure for TOPSIS
4.1. New Proposal (TOPSIS-AHP)
The synthesis procedure followed in TOPSIS combines the distances from the ideal and the anti-ideal solutions using the ratio (12) (Ri = 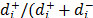 ). When the distance employed to measure proximity is the Euclidean (Step4), data are previously normalised using the Euclidean mode (11). If the distance employed is the Mahalanobis distance (14), then it is not necessary to normalize the original data (the results obtained when normalizing with any norm and not normalizing are the same).
). When the distance employed to measure proximity is the Euclidean (Step4), data are previously normalised using the Euclidean mode (11). If the distance employed is the Mahalanobis distance (14), then it is not necessary to normalize the original data (the results obtained when normalizing with any norm and not normalizing are the same).
As already mentioned, the results obtained for Ri, and therefore for the associated rankings, using both distances (Euclidean and Mahalanobis) can be clearly different if there is any dependence, even if it is very small. The new, AHP-based, procedure deals with this drawback, as well as the problem of selecting the method for normalizing the data; it further allows the assignation of a different relative importance for both distances. The rest of this section presents the new, AHP-based, procedure.
The Relative Importance Index (Wi) for alternative Ai i=1, ,m is given by:
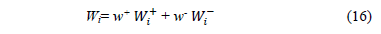
where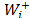 = w(
= w(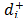 ) is the priority of
) is the priority of 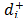 derived from the pairwise comparison matrix of the distances (
derived from the pairwise comparison matrix of the distances (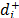 ) from alternative Ai to the ideal alternative A+ and w+ is the relative importance of the priorities of the distances to the ideal alternative. Analogously,
) from alternative Ai to the ideal alternative A+ and w+ is the relative importance of the priorities of the distances to the ideal alternative. Analogously, 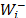 = w(
= w(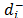 ) is the priority of
) is the priority of 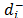 derived from the pairwise comparison matrix of the distances (
derived from the pairwise comparison matrix of the distances (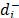 ) from alternative Ai to the anti-ideal alternative A- and w- is the relative importance of the priorities of the distances to the anti-ideal alternative.
) from alternative Ai to the anti-ideal alternative A- and w- is the relative importance of the priorities of the distances to the anti-ideal alternative.
In order to derive the priorities of the proximities to the ideal (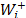 ) and to the anti-ideal (
) and to the anti-ideal (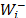 ) solutions for a particular distance (Euclidean, Mahalanobis etc.), the following pairwise comparison matrices should be constructed.
) solutions for a particular distance (Euclidean, Mahalanobis etc.), the following pairwise comparison matrices should be constructed.
a) In the first case (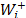 ), assuming that
), assuming that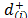 are the distances to the ideal solution (i)Î{1,
,m} in ascending order, the (r,s)-entry of the pairwise comparison matrix, from which the priorities (
are the distances to the ideal solution (i)Î{1,
,m} in ascending order, the (r,s)-entry of the pairwise comparison matrix, from which the priorities (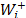 ) are derived, includes the judgment from Saaty's fundamental scale [18] that captures the intensity with which
) are derived, includes the judgment from Saaty's fundamental scale [18] that captures the intensity with which 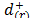 is preferred to
is preferred to 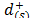 .
.
b) In the second case (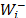 ), assuming that
), assuming that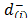 are the distances to the anti-ideal solution (i)Î{1,
,m} in descending order, the (r,s)-entry of the pairwise comparison matrix from which the priorities (
are the distances to the anti-ideal solution (i)Î{1,
,m} in descending order, the (r,s)-entry of the pairwise comparison matrix from which the priorities (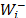 ) are derived includes the judgment from the Saaty's fundamental scale [18] that captures the intensity with which
) are derived includes the judgment from the Saaty's fundamental scale [18] that captures the intensity with which 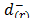 is preferred to
is preferred to 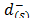 .
.
By means of any of the existing prioritization procedures (the Row Geometric Mean in this case), we derive for each alternative the priorities of its distances to the ideal and anti-ideal solutions (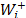 and
and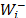 , respectively). Using these values and the relative importance or weight associated to the distances to the ideal and the anti-ideal solutions (w+ and w), the priority for each alternative is obtained (16) and used to rank them.
, respectively). Using these values and the relative importance or weight associated to the distances to the ideal and the anti-ideal solutions (w+ and w), the priority for each alternative is obtained (16) and used to rank them.
4.2. Case Study
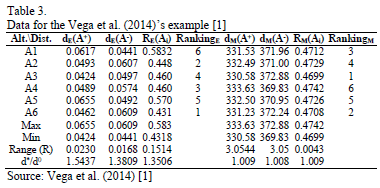
This procedure has been applied to the example (Profiles of Graduate Fellowship Applicants) used in Vega et al. [1]. The data corresponding to the distances to the ideal and the anti-ideal as well as the relative proximity (12) and the resulting rankings for the two distances (Euclidean and Mahalanobis) can be seen in Table 3.
It can be observed that the rankings obtained using TOPSIS-T (distance and Euclidean normalization) and TOPSIS-M (Mahalanobis distance and non-normalized data) are clearly different. This is also true for very small dependencies [1]. In our example, the value of the Gleason-Staelin measure of redundancy (Phi) is 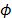 = 0.6736, which is higher than the 0.5 threshold necessary for the existence of dependence.
= 0.6736, which is higher than the 0.5 threshold necessary for the existence of dependence.
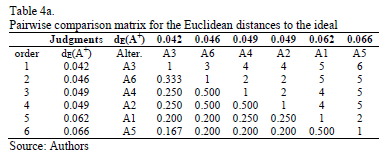
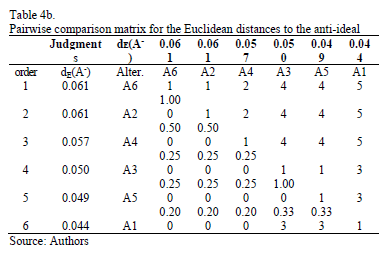
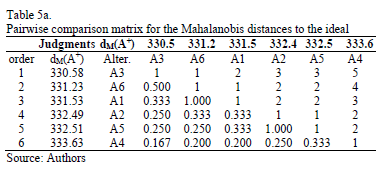
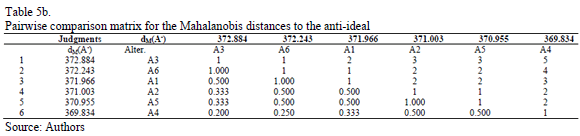
In order to deal with this conflict and after ranking the distances to the ideal and the anti-ideal from the minimum to the maximum, we ask the decision maker to evaluate the relative importance of the distances (Euclidean and Mahalanobis) to the ideal and the anti-ideal solutions. The pairwise comparisons matrices provided by the decision maker are given in Tables 4a and 4b for the Euclidean distance and in Tables 5a and 5b for the Mahalanobis distance.
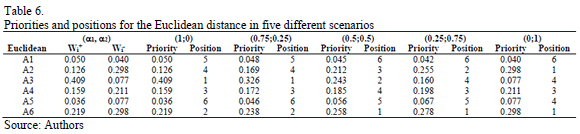
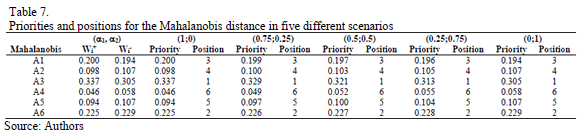
Using the Row Geometric Mean method as the prioritization procedure, the local priorities for the two distances (Euclidean and Mahalanobis) are obtained in five different scenarios, which depend on the weights assigned to the priorities of the distances to the ideal and the anti-ideal (see Tables 6 and 7).
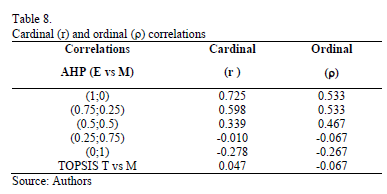
As can be noted in Tables 6 and 7, the Relative Importance Index (Wi) and rankings obtained for the two distances (Euclidean and Mahalanobis) with the new synthesis procedure (TOPSIS-AHP-E and TOPSIS-AHP-M) differ in the five considered scenarios, which depend on the weights given to the distances from the ideal and the anti-ideal. But both the cardinal (r) and ordinal (Spearman's r) correlations between them (TOPSIS-AHP-E and TOPSIS-AHP-M) are greater than those obtained for the TOPSIS-T and TOPSIS-M (see Table 8), except for the linear correlation in the (a1,a2) = (0.25; 0.75) situation.
It can also be verified that the cardinal and ordinal correlations between the values obtained with TOPSIS-T and with TOPSIS-AHP-E are greater than 90% in situation (a1,a2) = (0.25; 0.75). On the other hand, the greatest values for the correlations between TOPSIS-M and TOPSIS-AHP-M are reached for the situation (a1,a2) = (0; 1), with values closer to a 100%.
With respect to the judgment of Saaty's fundamental scale assigned by the decision maker to each comparison of distances, it should be mentioned that these judgments capture the holistic vision of the reality and are given in accordance with the decision maker's experience and culture.
It is not easy to assign these judgments in a systematic way because of the diversity of the distances for both metrics.
For the values of our example, we can suggest the following practical procedure, which depends on the values of the Range of the distances (R = d*-d0) and the ratio d*/d0, where d* = Maxi di and d0= Mini di with i=1. .m.
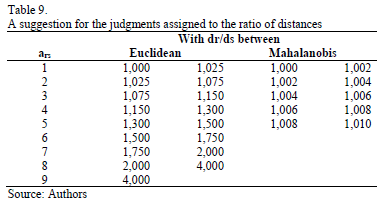
Let dr and ds be the two compared distances (dr³ ds) and assuming that the criterion for the comparisons is the higher the better, the judgment (ars) associated to the comparison between dr and ds for the Euclidean distance (d*/d0 =1.544 to the ideal and 1.381 to the anti-ideal) and the Mahalanobis distance are given in the scales included in Table 9.
Obviously, as it has already been mentioned, this suggestion depends on the considered distances (d*-d0 and d*/d0) and a more detailed study would be necessary in order to establish a systematic rule.
5. Conclusions
One of the limitations of TOPSIS in its initial proposal (Euclidean distance and normalization), known as traditional TOPSIS (TOPSIS-T), is the problem of dependence among the attributes. In order to solve this problem and capture the dependence among the attributes, [1] proposed the use of the Mahalanobis distance (no need to normalize the data) instead of the Euclidean. This extension of TOPSIS-T, known as TOPSIS-M, provides rankings for the alternatives being compared which can be significantly different, even for small degrees of dependence.
To deal with this problem, this paper proposes a new synthesis procedure for the distances of the alternatives from the ideal and the anti-ideal ones. The new Relative Importance Index integrates the relative importance of the distances to these two points and provides results for the Euclidean and the Mahalanobis distances that are closer than those obtained with TOPSIS-T and TOPSIS-M.
The new proposal aims to be a stepping-stone in the process of obtaining a synthesis procedure for the distances to the ideal and the anti-ideal that allows us to reduce the gap between the results obtained with dependent and independent attributes. The results, that appear to be justified by the relative importance captured by the AHP, should be tested with some other examples.
Acknowledgments
This work was partially financed by:
- Project "Industrial Optimization Processes Thematic Network", supported by the Mexican National Council for Science and Technology by agreement number 242104.
- Project "Social Cognocracy Network" (Ref. ECO2011-24181), supported by the Spanish Ministry of Science and Innovation. The authors also would like to acknowledge the work of English translation professional David Jones in preparing the final text.
References
[1] Vega, A., Aguarón, J., García-Alcaraz, J. and Moreno-Jiménez, J.M., Notes on dependent attributes in TOPSIS. Procedia Computer Science, 31, pp. 308-317. 2014. DOI: 10.1016/j.procs.2014.05.273 [ Links ]
[2] Behzadian, M., Otaghsara, S.K., Yazdani, M. and Ignatius, J.A State-of the-art survey of TOPSIS applications. Expert Systems with Applications, 39, pp. 13051-13069. 2012. DOI: 10.1016/j.eswa.2012.05.056 [ Links ]
[3] Hwang, C.L. and Yoon, K.P., Multiple attribute decision making: methods and applications survey. New York. NY: Springer-Verlag. 1981. DOI: 10.1007/978-3-642-48318-9 [ Links ]
[4] Kiang, M.Y., A Comparative assessment of classification methods. Decision Support Systems, 35, pp. 441-454, 2003. DOI: 10.1016/S0167-9236(02)00110-0 [ Links ]
[5] De Maesschalck, R., Jouan-Rimbaud, D. and Massart, D.L., The Mahalanobis distance. Chemo AC. Pharmaceutical Institute. Department of Pharmacology and Biomedical Analysis, 50, pp. 1-18. 2000. [ Links ]
[6] Mahalanobis, P.C., On the generalised distance in statistics. Proceedings National Institute of Science, 2 (1), pp. 49-55. 1936. [ Links ]
[7] Kovács, P., Petres, T. and Tóth, L., A. new measure of multicollinearity in linear regression models. International Statistical Review, 73 (3), pp. 405-412. 2005. DOI: 10.1111/j.1751-5823.2005.tb00156.x [ Links ]
[8] Moreno-Jiménez, J.M., El proceso analítico jerárquico. fundamentos. metodología y aplicaciones. RECT@ Revista Electrónica de Comunicaciones y Trabajos de ASEPUMA - Serie Monografías, 1, 35. 2002. [ Links ]
[9] Garza-Ríos, R. and González-Sánchez, C., Apply multicriteria methods for critical alternative selection. DYNA, 81 (188), pp. 125-130. 2014. DOI: 10.15446/dyna.v81n188.41220 [ Links ]
[10] Zeleny, M., Multiple criteria decision making. New York. NY. USA: Penguin Books. 1982. [ Links ]
[11] Belton, V. and Steward, J., Multiple criteria decision analysis - an integrated approach. Bolton: KluwerAcademic Pres. 2002. DOI: 10.1007/978-1-4615-1495-4 [ Links ]
[12] Yu, P.L. and Leitmann, G., Compromise solutions domination structures and Salukvadze's solution. Journal of Optimization Theory and Applications, 13, pp. 362-378. 1974. DOI: 10.1007/BF00934871 [ Links ]
[13] Zeleny, M., Compromise programming. In Multicriteria Decision Making. ed. by J.L. Cochrane and M. Zeleny, South Carolina. USA: University of Columbia Press. 1973. [ Links ]
[14] Charnes, A., Cooper, W.W. and Ferguson, R., Optimal estimation of excutive compensation by linear programming. Management Science, 1, pp. 138-151. 1955. DOI: 10.1287/mnsc.1.2.138 [ Links ]
[15] Opricovic, S. and Tzeng, G., Multicriteria planning of post-earthquake sustainable reconstruction. Computer-Aided Civil and Infrastructure Engineering, 17, pp. 211-220. 2002. DOI: 10.1111/1467-8667.00269 [ Links ]
[16] Chen, S.J. and Hwang, C.L., Fuzzy multiple attribute decision making: Methods and applications. Berlin: Springer-Verlag. 1992. DOI: 10.1007/978-3-642-46768-4 [ Links ]
[17] Yoon, K.P. and Hwang, C.L., Multiple attribute decision making. Thousand Oaks. CA: Sage Publication. 1995. [ Links ]
[18] Saaty. T.L., The analytic hierarchy process. McGraw-Hill. New York. 1980. [ Links ]
[19] Saaty. T.L., Fundamentals of decision making and priority theory with the analytic hierarchy process. RWS Publications. Pittsburgh. PA. 1994. [ Links ]
[20] Aguarón, J. and Moreno-Jiménez, J.M., The geometric consistency index: Approximated thresholds. European Journal of Operational Research, 147 (1), pp. 137-145. 2003. DOI: 10.1016/S0377-2217(02)00255-2 [ Links ]
[21] Bilbao-Terol, A., Arenas-Parra, M., Cañal-Fernández, V. and Antomil-Ibias, J., Using topsis for assessing the sustainability of government bond funds. Omega, 49, pp. 1-17. 2014. DOI: 10.1016/j.omega.2014.04.005 [ Links ]
[22] Lima, F.R., Osiro, L. and Ribeiro, L.C., A comparison between Fuzzy AHP and Fuzzy TOPSIS methods to supplier selection. Applied Soft Computing, 21, pp. 194-209. 2014. DOI: 10.1016/j.asoc.2014.03.014 [ Links ]
[23] Wang, J.W., Cheng, C.H. and Huang, K.C., Fuzzy hierarchical TOPSIS for supplier selection. Applied Soft Computing, 9, pp. 377-386. 2009. DOI: 10.1016/j.asoc.2008.04.014 [ Links ]
[24] Lipovetsky, S. and Michael Conklin, W., Multiobjective regression modifications for collinearity. Computers & Operations Research, 28, pp. 1333-1345. 2001. DOI: 10.1016/S0305-0548(00)00043-5 [ Links ]
[25] Pasini, A., A Bound for the collinearity graph of certain locally polar geometries. Journal of Combinatorial Theory. Series A, 58, pp. 127-130. 1991. DOI: 10.1016/0097-3165(91)90077-T [ Links ]
[26] Liu, R.X., Kuang, J., Gong, Q. and Hou, X.L., Principal component regression analysis with Spss. Computer Methods and Programs in Biomedicine, 71, pp. 141-17. 2003. DOI: 10.1016/S0169-2607(02)00058-5 [ Links ]
[27] Li, B., Morris, A.J. and Martin, E.B., Generalized partial least squares regression based on the penalized minimum norm projection. Chemometrics and Intelligent Laboratory Systems, 72, pp. 21-26. 2004. DOI: 10.1016/j.chemolab.2004.01.026 [ Links ]
[28] Jackson, J., A User's guide to principal components. New York: John Wiley &Sons. 1991. DOI: 10.1002/0471725331 [ Links ]
J. Aguarón-Joven is an Associate Professor of Statistics and Operations Research at the Business and Economics Faculty of the University of Zaragoza, Spain. He holds a PhD in Mathematics by the University of Zaragoza, Spain and belongs to the Multicriteria Decision Making Group at this same University. His main research interests are Multicriteria Decision Making, Decision Support Systems and Information Systems. He has published several papers in journals such as the European Journal of Operational Research, Group Decision and Negotiation, or Annals of Operations Research, as well as many book chapters and proceedings. ORCID: 0000-0003-3138-7597.
M.T. Escobar-Urmeneta is an Associate Professor of Statistics and Operations Research at the Business and Economics Faculty of the University of Zaragoza, Spain. She holds a PhD in Mathematics by the University of Zaragoza, Spain. She belongs to the Multicriteria Decision Making Group at this same University (http://gdmz.unizar.es), and her main research interests are Multicriteria Decision Making, especially with the Analytic Hierarchy Process (AHP) and its application to several fields such as Logistics, Environment, E-Government, etc. She has published several papers in journals such as the European Journal of Operational Research, Omega, Group Decision and Negotiation, Computers and Human Behavior or Annals of Operations Research, as well as many book chapters and proceedings. ORCID: 0000-0003-4419-1905.
J.L. García-Alcaraz is currently a full professor in the department of Industrial and Manufacturing Engineering at the Autonomous University of Ciudad Juarez, Mexico. He is a founding member of the Mexican Society of Operations Research, active member of the Mexican Academy of Industrial Engineering and honorary member of the Mexican Association of Logistics and Supply Chain. Dr. Garcia is recognized as researcher level I by the National Council of Science and Technology of Mexico (CONACYT). He received a Master's Degree in Industrial Engineering Sciences from the Technological Institute of Colima, Mexico, a Ph.D. in Industrial Engineering Sciences from the Technological Institute of Ciudad Juarez, Mexico and a Post-Doctorate at the University of La Rioja, Spain. His main researches areas are related to the modeling production processes and multi-criteria decision-making applied supply chain. He is author-coauthor of over 100 articles published in journals, conferences and congresses. ORCID: 0000-0002-7092-6963.
J.M. Moreno-Jiménez completed degrees in mathematics and economics as well as a PhD. degree in applied mathematics from the University of Zaragoza, Spain. He is a Full Professor of Operations Research and Multicriteria Decision Making in the Faculty of Economics and Business of the University of Zaragoza, Spain. He is also the Chair of the Zaragoza Multicriteria Decision Making Group (http://gdmz.unizar.es), a research group attached to the Aragon Institute of Engineering Research (I3A), the Coordinator of the Spanish Multicriteria Decision Making Group and the President of the International Society on Applied Economics ASEPELT. His main fields of interest are multicriteria decision-making, environmental selection, strategic planning, knowledge management, evaluation of systems, logistics, and public decision making (e-government, e-participation, e-democracy and e-cognocracy). He has published more than 200 papers in scientific books (LNCS, LNAI, CCIS, Advances in Soft Computing ) and journals such as Operations Research, European Journal of Operational Research, Omega, Group Decision and Negotiation, Annals of Operations Research, Computer, Standards and Interface, Mathematical and Computer Modeling, Computers in Human Behavior, International Journal of Production Research, Journal of Multi-Criteria Analysis, Int. J. Social and Humanistic Computing, Production Planning & Control, Government Information Quaterly, EPIO (Argentina), Pesquisa Operativa (Brasil), Revista Eletrônica de Sistemas de Informação (Brasil), TOP (España), Estudios de Economía Aplicada (España), and Computación y Sistemas (Méjico), among others. He is a member of the Editorial Board of two national (Spanish) journals (EEA y CAE) and five international ones (IJAHP, IJKSR, RIJSISEM, JMOMR, ITOR). ORCID: 0000-0002-5037-6976.
A. Vega-Bonilla is a Master of Science in Industrial Engineering by Autonomous University of Ciudad Juárez, Mexico and Bachelor of Science in Mechatronics Engineering by Monterrey Institute of Technology and Higher Education campus Chihuahua, Mexico. He had also a research fellowship by the National Council for Science and Technology (CONACyT), during his Master degree studies. Vega-Bonilla has work experience in the manufacturing, logistics and transportation fields. He has served as a volunteer in the New Mexico International Business Accelerator (USA government association) organizing the main conference "NAFTA Institute / Supplier meet the Buyer" in 2011. He was also General Coordinator in organizing the 3rd. International Engineering Congress with the theme "Green Engineering and Sustainable Development" and he was Member of Mechatronics Engineering Student Society SAIMT 09-10. His research has ranged over multicriteria decision making theory and industrial environment philosophy.