Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.191 Medellín May/June 2015
DOI: http://dx.doi.org/10.15446/dyna.v82n191.51147
Short-term generation planning by primal and dual decomposition techniques
Planeación de la generación a corto plazo mediante técnicas de descomposición primal y dual
José Antonio Marmolejo-Saucedo a & Román Rodríguez-Aguilar b
a Facultad de Ingeniería, Universidad Anáhuac México Norte, Mexico, D.F., México. jose.marmolejo@anahuac.mx
b Escuela Superior de Economía, Instituto Politécnico Nacional, Mexico, D.F., México. roman.rodriguez@ipn.mx
Received: January 28th, 2015. Received in revised form: March 26th, 2015. Accepted: April 30th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
This paper addresses the short-term generation planning (STGP) through thermoelectric units. The mathematical model is presented as a Mixed Integer Non Linear Problem (MINLP). Several works on the state of art of the problem have revealed that the computational effort of this problem grows exponentially with the number of time periods and number of thermoelectric units. Therefore, we present two alternatives to solve a STGP based on Benders' partitioning algorithm and Lagrangian relaxation in order to reduce the computational effort. The proposal is to apply primal and dual decomposition techniques, which exploit the structure of the problem to reduce solution time by decomposing the STGP into a master problem and a subproblem. For Benders' algorithm, the master problem is a Mixed Integer Problem (MIP) and for the subproblem, it is a Non Linear Problem (NLP). For Lagrangian relaxation, the master problem and the subproblem are MINLP. The computational experiments show the performance of both decomposition techniques applied to the STGP. These techniques allow us to save computation time when compared to some high performance commercial solvers.
Keywords: Benders' algorithm; Lagrangian relaxation; subgradient; decomposition techniques; power generation.
Resumen
En este trabajo se aborda la planeación de la generación a corto plazo (STGP) a través de las unidades termoeléctricas. El modelo matemático se presenta como un problema no lineal entero mixto (MINLP). Varios trabajos del estado del arte del problema han revelado que el esfuerzo computacional de este problema crece exponencialmente con el número de períodos de tiempo y número de unidades termoeléctricas. Por lo tanto, presentamos dos alternativas para resolver la planeación de la generación a corto plazo (STGP) basadas en el algoritmo de partición Benders y relajación lagrangiana con la finalidad de reducir el esfuerzo computacional. La propuesta consiste en aplicar técnicas de descomposición primal y dual que explotan la estructura del problema para reducir el tiempo de solución mediante la descomposición de la planeación de la generación a corto plazo (STGP) en un problema maestro y un subproblema. Para el algoritmo de Benders el problema maestro es un problema entero mixto (MIP) y para el subproblema es un problema no lineal (NLP). Para la relajación lagrangeana, el problema maestro y el subproblema son MINLP. Los experimentos computacionales muestran el rendimiento de ambas técnicas de descomposición aplicadas a la planeación de la generación a corto plazo (STGP). Estas técnicas permiten ahorrar tiempo de cálculo en comparación con algunos optimizadores comerciales de alto rendimiento.
Palabras clave: Algoritmo de Benders; relajación lagrangiana; subgradiente; técnicas de descomposición; generación eléctrica.
1. Short-term generation planning
The efficient short term generation planning of available energy resources for satisfying load demand has become an important task in modern power systems [14,17].
A definition of short-term generation planning (Unit commitment) is the operation of generation facilities to produce energy at the lowest cost to reliably serve consumers, recognizing any operational limits of generation facilities. The problem consists of deciding which units must be used over a given planning horizon, usually 24 time periods.
In the typical Unit Commitment [5], the transmission network is not considered, so for this case we considered network constraints, and the problem consists of determining the mix of generators and their estimated output level to meet the expected demand of electricity over a given time horizon (a day or a week), while satisfying the load demand, spinning reserve requirement and transmission network constraints. An electric network consists of many generation nodes with various generating capacities and cost functions, lines of transmission and nodes of power demand [7,9,12].
Over the past few years, several studies have been conducted to define appropriate models and algorithms in order to obtain the optimal solution of the STGP. There are many optimization techniques for solving this problem, the major solution approaches are decomposition techniques, branch-and-bound techniques, and metaheuristics [15,16].
Since the Short Term Generation Scheduling (STGS) with network constraints is a NP-hard Mixed Integer Non Linear Problem, for large power systems, exact methods proved to be inefficient [10]. Because of this, we present an alternative to generating quality bounds in short computing time based on primal and dual decomposition.
2 The Model

The problem STGP is defined as follows:
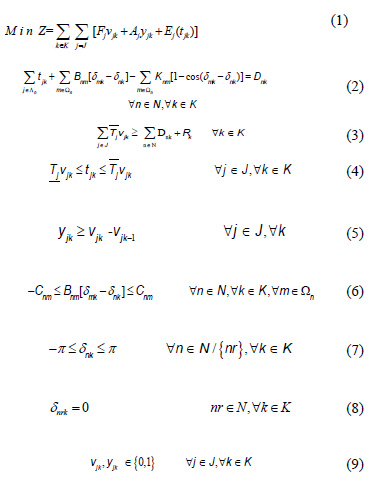
The objective eq. (1) minimizes the start up cost 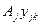 and operating cost of each plant. The operating cost of each plant
and operating cost of each plant. The operating cost of each plant  is included a fixed cost
is included a fixed cost  and a variable cost
and a variable cost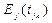 .
.
There is a power balance constraint eq. (2) per node and time period. In each period, the production has to satisfy the demand and losses in each node. Power line losses are modeled through cosine approximation and it is assumed that the demand for electric energy is known and is discretized into t periods. There are many approximations to model power line losses, some of them are linear and non-linear approximations. Further details of the cosine approximation can be found in [1].
Spinning reserve requirements are modeled in eq. (3). In each period the running units have to be able to satisfy the demand and the prespecified spinning reserve.
In eq. (4), each unit has a technical lower and upper bound for the power production. Transmission capacity limits of lines eq. (5) avoid dynamic stability system problems. The constraint eq. (6) holds the logic of running, start-up and shut-down of the units.
A running unit cannot be started-up. Finally, angle in all buses has a lower and upper bound eq. (7).
3. Benders' Decomposition
Benders Decomposition has been successfully applied to take advantage of underlying problem structures for various optimization problems, such as planning of power systems. The basic idea of this method is the generation, at each iteration, of an upper bound and lower bound on the sought solution of the problem. The upper bound results from the primal subproblem, while the lower bound results from the master problem [1].
Benders' Master Problem:
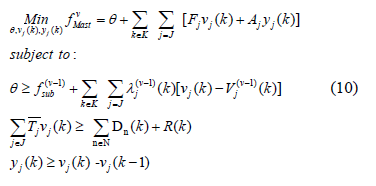
Benders Subproblem:
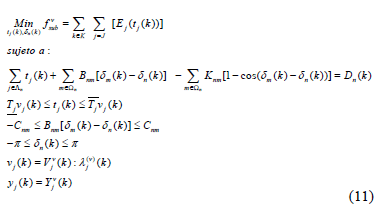
4. Lagrangian Relaxation
Lagrangian relaxation [2,8,11] decomposes the STGP into a master problem and makes it easier to solve subproblems separately. The subproblems are linked by Lagrange Multipliers that are added to the master problem to yield a dual problem. The dual problem has lower dimensions than the primal problem and is easier to solve. The multipliers are updated through different methods, usually a subgradient method. The major difficulty of this method is associated with obtaining solution feasibility because of the dual nature of the algorithm.
Dual Master Problem:
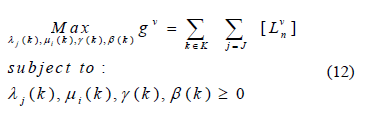
Dual Subproblem:
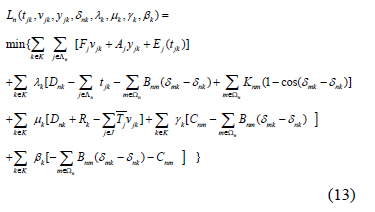
Subject to eq. (4, 5, 7, 8, 9)
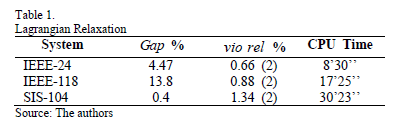
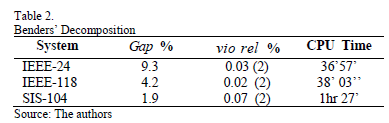
5. Computational experimentation
Three test systems are presented to evaluate the performance of the proposed AGS algorithm.
- The IEEE 24 bus test system with 24 nodes, 24 thermal units and 38 transmission lines [3,6].
- A portion of bus electric energy system of Mainland Spain with 104 nodes, 62 thermal units and 160 transmission lines [1].
- The IEEE 118 bus test system with 118 nodes, 54 thermal units and 186 transmission lines [13].
For Lagrangian relaxation, the mathematical model of STGP were implemented in GAMS [4] using the DICOPT solver for solving the MINLP problems (dual subproblems). CONOPT for solving the NLP problems (primal subproblems) and CPLEX for MIP problems (master primal problem).
All the models have been solved on an AMD Phenom II N970 Quad-Core with a 2.2 GHz processor and 8 GB RAM.
NLP and MINLP solvers were tuned to obtain solutions with a tolerance of 10% optimality. Therefore, the master and subproblems solutions obtained from the solvers are almost feasible and good solutions.
The iterative procedure continues until some stopping criterion is reached. For this case, the stopping criterion was 0.1 % of optimality of the MINLP solver.
Conclusions
We evaluated the performance of primal and dual decomposition techniques in order to compare the quality of the solutions they provide Three test systems are presented to evaluate the performance of the proposed solution methods. Although for the MINLPs' problems global optimality is not guaranteed, the proposed strategies show good convergence properties and provide better results than those obtained solving the problem using other methods. Thus, this application can be extended to large scale problems.
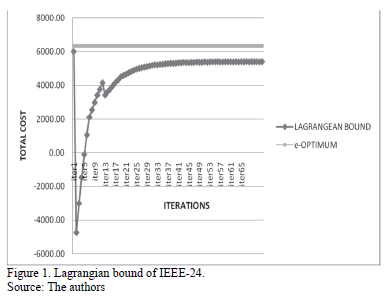
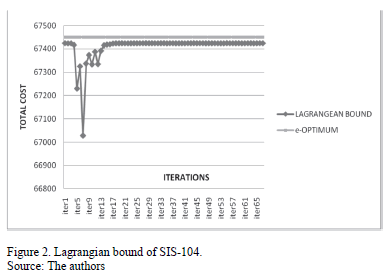
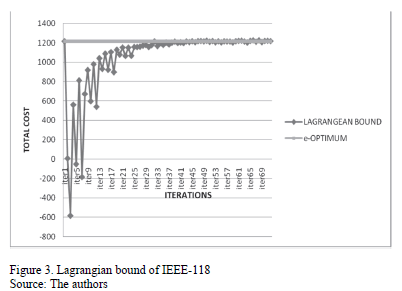
Through the results, we see a decrease in computational time by Lagrangian relaxation of the problem, as well as lower Gap. See Figs.1, 2 and 3.
However, the percentage of  increases due to relaxation of system constraints. The solution obtained by Lagrangian relaxation is sometimes infeasible to the original problem, so to achieve the feasibility of the problem we propose using lower thermal plants cost as part of the vector of solutions that would provide electricity generation to meet demand requirements in all periods.
increases due to relaxation of system constraints. The solution obtained by Lagrangian relaxation is sometimes infeasible to the original problem, so to achieve the feasibility of the problem we propose using lower thermal plants cost as part of the vector of solutions that would provide electricity generation to meet demand requirements in all periods.
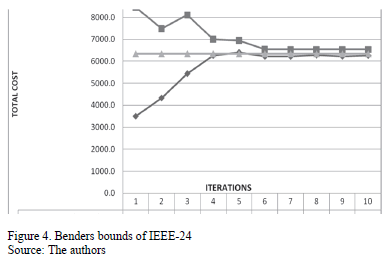
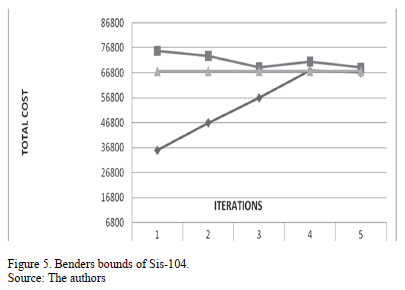
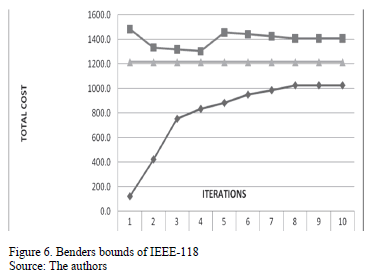
By contrast, in Benders' decomposition, there is no feasibility loss because the problem retains the same set of constraints. However, through experimentation, we observed a small percentage of relative deviation attributable to the optimizer. See Figs. 4, 5, 6.
References
[1] Alguacil, N. and Conejo, A,. Multiperiod optimal power flow using benders decomposition. IEEE Transactions on power systems,15 (1), pp 196-201, 2000. DOI: 10.1109/59.852121 [ Links ]
[2] Guignard, M., Lagrangean relaxation. Top,11 (2), pp 151-228, 2003. DOI: 10.1007/BF02579036 [ Links ]
[3] Charman, P.F., Bhavaraju, M.P., Billington, R. et al., IEEE reliability test system. IEEE Transactions on power apparatus and systems, 98 (6), pp 2047-2054, 1979. [ Links ]
[4] Brooke, A. and Kendrick, D., GAMS-The solver manuals. GAMS/COIN. GAMS Development Corporation. Washington, 2007. [ Links ]
[5] Wood, A.J. and Wollenberg, B., Power generation operation and control, New York: John Wiley and Sons, Inc,1996. [ Links ]
[6] Grigg, C., Whong, P., Albretch, P., Allan, R. et al., The IEEE reliability test system-1996. IEEE Transactions on power systems, 14 (3), pp 1010-1020, 1999. DOI: 10.1109/59.780914 [ Links ]
[7] Granada, M., Rider, M., Mantovani, J. and Shahidehpour, M., Multi-areas optimal reactive power flow. In Transmission and Distribution Conference and Exposition: Latin America, 2008 IEEE/PES, pp 1-6, 2008. [ Links ]
[8] Ruzic, S. and Rajakovic, N., A new approach for solving extended unit commitment problem. Power Systems, IEEE Transactions on, 6 (1), pp 269-277, 1991. [ Links ]
[9] Guo, S., Guan, X. and Zhai, Q., The necessary and sufficient conditions for determining feasible solutions to unit commitment problems with ramping constraints. In Power Engineering Society General Meeting, 2005. IEEE, 1, pp 344-349, 2005. [ Links ]
[10] Sheble, G. and Fahd, G., Unit commitment literature synopsis. IEEE Transactions on Power Systems, 9 (1), pp 128-135, 1994. DOI: 0.1109/59.317549 [ Links ]
[11] Salam, M.S., Nor, K. and Hamdam, A.R., Hydrothermal scheduling based lagrangian relaxation approach to hydrothermal coordination. IEEE Transactions on Power Systems, 13 (1), pp 226-235, 1998. DOI: 10.1109/59.651640 [ Links ]
[12] Carpentier, J., Optimal power flows. Int. J. Elect. Power Energy Syst., 1 (1). pp 3-15, 1979. DOI: 10.1016/0142-0615(79)90026-7 [ Links ]
[13] Marmolejo, J.A. and Rodríguez, R., Fat tail model for simulating test systems in multiperiod unit commitment, Mathematical Problems in Egineering, in press, 2015. DOI: 10.1155/2015/738215 [ Links ]
[14] Ortiz-Pimiento, N.R. and Diaz-Serna, F.J., Validación de soluciones obtenidas para el problema del despacho hidrotérmico de mínimo costo empleando la programación lineal binaria mixta. DYNA [Online]. 75 (156), pp. 43-54. 2008, [date of reference november 30th of 2014]. Available at: http://www.scielo.org.co/scielo.php?script=sci_arttext&pid=s0012-73532008000300004&lng=en&nrm=iso. issn 0012-7353. [ Links ]
[15] Gallego-Vega, L.E. and Duarte-Velasco, O.G.. Modeling of bidding prices in power markets using clustering and fuzzy association rules. DYNA [Online], 78 (166), pp. 108-117, 2011. [date of reference: november 30th of 2014]. Available at: http://www.redalyc.org/articulo.oa?id=49622365014. issn 0012-7353 [ Links ]
[16] Medina, M.A., Ramirez, J.M., Coello, C.A., and Das, S., Use of a multi-objective teaching-learning algorithm for reduction of power losses in a power test system, DYNA [Online], 81 (185), pp. 196-203, 2014. [date of reference: november 30th of 2014]. Available at: http://www.redalyc.org/articulo.oa?id=49631031029. issn 0012-7353 [ Links ]
[17] Gimenez-Alvarez, J.M., Schweickardt, G. and Gómez-Targarona, J.C., An overview of wind energy, taking into consideration several important issues including an analysis of regulatory requirements for the connection of wind generation into the power system. DYNA [Online], 79 (172), pp. 108-117, 2012. [date of reference: november 30th of 2014]. Available at: http://www.redalyc.org/articulo.oa?id=49623221013. issn 0012-7353 [ Links ]
J.A. Marmolejo, is a professor in the Faculty of Engineering at Universidad Anahuac Mexico Norte, Mexico. He has a PhD. in Engineering specializing in Operations Research from the National Autonomous University of Mexico and is currently a member of the National System of Researchers of the National Council of Science and Technology (CONACYT) of Mexico. He is on the Board of the Mexican Society of Operations Research. His areas of interest are large scale optimization and mathematical modeling in power systems and logistical problems in the supply chain.
R. Rodriguez, has a PhD. in Economics specializing in mathematical finance obtained from the School of Economics at the National Polytechnic Institute, a MSc. degree in Engineering and Statistics from the National Autonomous University of Mexico, a MSc. degree in Public Policy from the Institute of Technology and Research superiors of Monterrey. Dr. Rodriguez is a member of the Mexican Mathematical Society, the National Association of Economists and Economic Modeling Network EcoMod. His areas of interest are stochastic optimization, mathematical finance and econometrics.