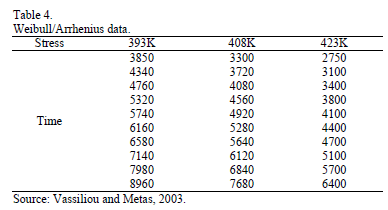Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.191 Medellín May/June 2015
https://doi.org/10.15446/dyna.v82n191.43533
DOI: http://dx.doi.org/10.15446/dyna.v82n191.43533
Weibull accelerated life testing analysis with several variables using multiple linear regression
Análisis de pruebas de vida acelerada Weibull con varias variables utilizando regresión lineal múltiple
Manuel R. Piña-Monarrez a, Carlos A. Ávila-Chávez b & Carlos D. Márquez-Luévano c
a Industrial and Manufacturing department of the IIT Institute, Universidad Autónoma de Ciudad Juárez, Chihuahua , México. manuel.pina@uacj.mx
b Industrial and manufacturing deparment of the IIT Institute, Universidad Autónoma de Ciudad Juárez, Chihuahua , México. carlos.avila@uacj.mx
c Reliability Engineering Department at Stoneridge Electronics North America. carlos.marquez@stoneridge.com
Received: May 16th, 2014. Received in revised form: February 24th, 2015. Accepted: March 04th, 2015
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
In Weibull accelerated life test analysis (ALT) with two or more variables  , we estimated, in joint form, the parameters of the life stress model
, we estimated, in joint form, the parameters of the life stress model  and one shape parameter
and one shape parameter 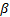 . These were then used to extrapolate the conclusions to the operational level. However, these conclusions are biased because in the experiment design (DOE) used, each combination of the variables presents its own Weibull family
. These were then used to extrapolate the conclusions to the operational level. However, these conclusions are biased because in the experiment design (DOE) used, each combination of the variables presents its own Weibull family 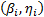 . Thus the estimated
. Thus the estimated 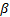 is not representative. On the other hand, since
is not representative. On the other hand, since 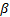 is determined by the variance of the logarithm of the lifetime data
is determined by the variance of the logarithm of the lifetime data 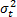 , the response variance
, the response variance 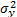 and the correlation coefficient
and the correlation coefficient 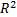 , which increases when variables are added to the analysis,
, which increases when variables are added to the analysis, 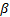 is always overestimated. In this paper, the problem is statistically addressed and based on the Weibull families
is always overestimated. In this paper, the problem is statistically addressed and based on the Weibull families 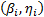 a vector
a vector 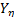 is estimated and used to determine the parameters of
is estimated and used to determine the parameters of 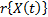 . Finally, based on the variance
. Finally, based on the variance 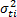 of each level, the variance of the operational level
of each level, the variance of the operational level 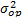 is estimated and used to determine the operational shape parameter
is estimated and used to determine the operational shape parameter 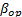 . The efficiency of the proposed method is shown by numerical applications and by comparing its results with those of the maximum likelihood method (ML).
. The efficiency of the proposed method is shown by numerical applications and by comparing its results with those of the maximum likelihood method (ML).
Keywords: ALT analysis; Weibull analysis; multiple linear regression; experiment design.
Resumen
En el análisis de pruebas de vida acelerada Weibull con dos o más variables aceleradas 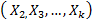 , estimamos en forma conjunta los parámetros del modelo de relación vida esfuerzo
, estimamos en forma conjunta los parámetros del modelo de relación vida esfuerzo 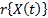 y un parámetro de forma
y un parámetro de forma 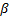 . Después estos parámetros son utilizados para extrapolar las conclusiones al nivel operacional. Como sea, estas conclusiones están sesgadas debido a que dentro del diseño de experimentos (DOE) utilizado, cada combinación de las variables presenta su propia familia Weibull
. Después estos parámetros son utilizados para extrapolar las conclusiones al nivel operacional. Como sea, estas conclusiones están sesgadas debido a que dentro del diseño de experimentos (DOE) utilizado, cada combinación de las variables presenta su propia familia Weibull 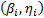 . De esa forma la
. De esa forma la 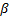 estimada no es representativa. Por otro lado, dado que
estimada no es representativa. Por otro lado, dado que 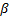 está determinada por la varianza del logaritmo de los tiempos de vida
está determinada por la varianza del logaritmo de los tiempos de vida 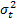 , por la varianza de la respuesta
, por la varianza de la respuesta 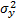 y por el coeficiente de correlación
y por el coeficiente de correlación 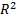 , el cual crece cuando se agregan variables al análisis,
, el cual crece cuando se agregan variables al análisis, 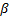 es siempre sobre estimada. En éste artículo, el problema es estadísticamente identificado y basado sobre las familias Weibull
es siempre sobre estimada. En éste artículo, el problema es estadísticamente identificado y basado sobre las familias Weibull 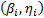 un vector
un vector 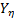 es estimado y utilizado para determinar los parámetros de
es estimado y utilizado para determinar los parámetros de 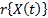 . Finalmente, basado en la varianza
. Finalmente, basado en la varianza 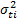 de cada nivel, la varianza del nivel operacional
de cada nivel, la varianza del nivel operacional 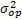 es estimada y utilizada para determinar el parámetro de forma
es estimada y utilizada para determinar el parámetro de forma 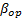 del nivel operacional. La eficiencia del método propuesto es mostrada a través de aplicaciones numéricas y por la comparación de sus resultados con los del método de máxima verosimilitud (ML).
del nivel operacional. La eficiencia del método propuesto es mostrada a través de aplicaciones numéricas y por la comparación de sus resultados con los del método de máxima verosimilitud (ML).
Palabras clave: ALT análisis; análisis Weibull; regresión lineal múltiple; diseño de experimentos.
1. Introduction
In Accelerated Life Testing analysis (ALT) with constant over time and interval-valued variables 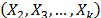 , the standard approach of the analysis consists in using higher levels of the stress variables and a life-stress model
, the standard approach of the analysis consists in using higher levels of the stress variables and a life-stress model 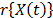 , the lifetime data are obtained as quickly as possible [6]. In this approach, the function
, the lifetime data are obtained as quickly as possible [6]. In this approach, the function 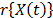 , which relates the lifetime data to the stress variables, is parametrized as
, which relates the lifetime data to the stress variables, is parametrized as
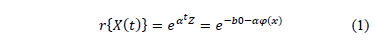
Where 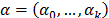 is a vector of unknown parameters, and
is a vector of unknown parameters, and 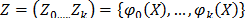 is a vector of specified functions
is a vector of specified functions 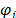 with
with 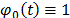 . Among the most common models of
. Among the most common models of 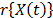 we have the generalized Eyring model, the temperature-humidity model (T-H), the temperature-non-thermal model, the proportional hazard model and the generalized log-linear model [9] and [13]. On the other hand, in ALT Weibull analysis no matter which model we use, all of them are used to estimate the scale parameter
we have the generalized Eyring model, the temperature-humidity model (T-H), the temperature-non-thermal model, the proportional hazard model and the generalized log-linear model [9] and [13]. On the other hand, in ALT Weibull analysis no matter which model we use, all of them are used to estimate the scale parameter 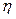 under different levels of the significant variables. For example if the (T-H) model is used, then in the Weibull probability density function (pdf) ([19] and [16] Chapter 1), given by
under different levels of the significant variables. For example if the (T-H) model is used, then in the Weibull probability density function (pdf) ([19] and [16] Chapter 1), given by
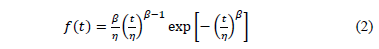
by replacing 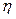 with the
with the 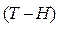 model the Weibull/(T-H) pdf is given by
model the Weibull/(T-H) pdf is given by
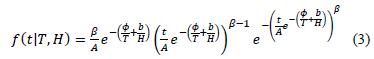
Unfortunately, since in (3) only one shape parameter 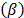 is estimated and used to represent all the level combinations of the variables, and because the maximum likelihood (ML) or multiple linear regression (MLR) methods perform the estimation as linear combination of
is estimated and used to represent all the level combinations of the variables, and because the maximum likelihood (ML) or multiple linear regression (MLR) methods perform the estimation as linear combination of  with the coefficients of the vector
with the coefficients of the vector 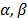 is always overestimated. As a consequence, the related reliability
is always overestimated. As a consequence, the related reliability 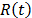 is overestimated too. In order to show this problem, in section 2 the generalities of ALT analysis are given. Section 3 presents the problem statement. In section 4 the problem is statistically addressed. Section five details the proposed method and, finally, in section 6 the conclusions are presented.
is overestimated too. In order to show this problem, in section 2 the generalities of ALT analysis are given. Section 3 presents the problem statement. In section 4 the problem is statistically addressed. Section five details the proposed method and, finally, in section 6 the conclusions are presented.
2. Generalities of Weibull ALT analysis
In ALT analysis, the objective is to obtain life data as quickly as possible. Data are obtained by observing a set of n units functioning under various levels of the explanatory variables 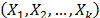 . These levels are chosen to be higher than the normal one. With these life data, we draw conclusions and then, the conclusions are extrapolated to the normal level. Models used to perform the extrapolation are known as life-stress models
. These levels are chosen to be higher than the normal one. With these life data, we draw conclusions and then, the conclusions are extrapolated to the normal level. Models used to perform the extrapolation are known as life-stress models 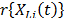 . Among the most common
. Among the most common 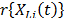 models we have the parametric accelerated failure time models (AFT) (e.g. Arrhenius model) [8], and the proportional hazard model (PH) (e.g. Weibull proportional hazard model) [5] and [1]. On the other hand, in the analysis, the lifetime data T is a nonnegative and absolute continuous random variable. Thus, the survival function is
models we have the parametric accelerated failure time models (AFT) (e.g. Arrhenius model) [8], and the proportional hazard model (PH) (e.g. Weibull proportional hazard model) [5] and [1]. On the other hand, in the analysis, the lifetime data T is a nonnegative and absolute continuous random variable. Thus, the survival function is 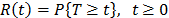 . And based on this, the corresponding probability density function is
. And based on this, the corresponding probability density function is 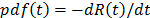 and the hazard rate function is
and the hazard rate function is 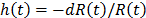 . Additionally, it is important to note that in ALT, the effect that the covariates
. Additionally, it is important to note that in ALT, the effect that the covariates 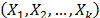 have over T, is modeled by
have over T, is modeled by 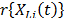 , which as in (3) is included in
, which as in (3) is included in 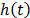 . On the other hand, for constant over time and interval valued variables, the cumulative risk function is
. On the other hand, for constant over time and interval valued variables, the cumulative risk function is 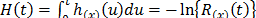 with
with 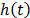 parametrized as
parametrized as 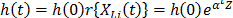 where
where 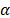 and Z are as they were defined in (1), and
and Z are as they were defined in (1), and 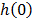 represents the base risk when all the covariates are zero
represents the base risk when all the covariates are zero 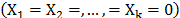 . For example, based on this formulation and on the physical principle of Sedyakin [1], pp. 20), the survival function for two different levels of the variables
. For example, based on this formulation and on the physical principle of Sedyakin [1], pp. 20), the survival function for two different levels of the variables 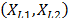 is related by
is related by 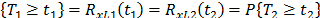 . Implying that
. Implying that 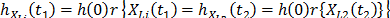 which in terms of
which in terms of 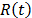 mean that
mean that 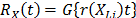 , and since the survival function
, and since the survival function 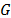 does not depend on
does not depend on 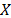 , then the random variable
, then the random variable 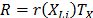 does not depend on X either. In particular observe that, since the expected value of
does not depend on X either. In particular observe that, since the expected value of 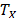 is
is 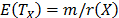 and its variance is
and its variance is 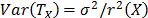 , then its variation coefficient
, then its variation coefficient 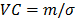 does not depend on
does not depend on 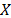 either. Thus, for any two stress levels (or variables combination), the distribution is the same, implying that only the scale changes (see [1] sec. 2.3). Observe the fact that the scale only changing in the Weibull analysis implies that
either. Thus, for any two stress levels (or variables combination), the distribution is the same, implying that only the scale changes (see [1] sec. 2.3). Observe the fact that the scale only changing in the Weibull analysis implies that
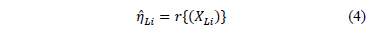
On the other hand, R(t) under any two levels 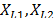 is related by
is related by 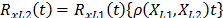 where
where
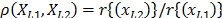 and that it is called the acceleration factor. Finally, it is important to note that by setting
and that it is called the acceleration factor. Finally, it is important to note that by setting 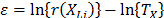 or
or 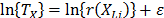 , and because
, and because 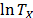 and
and 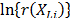 do not depend on
do not depend on 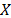 , then as in (5), the variance of
, then as in (5), the variance of 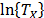 does not depend on
does not depend on 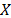 either.
either.
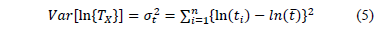
Despite of this, because in the estimation of the Weibull life-stress relationship as in (3), we estimate only one  value as a linear combination of the variables
value as a linear combination of the variables 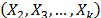 ,
,  is always overestimated as in the following section.
is always overestimated as in the following section.
3. Problem statement
Statement 1: Because in ALT failure time data is obtained by increasing the level of the variables 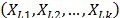 , the variance of the logarithm of the lifetimes
, the variance of the logarithm of the lifetimes 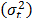 defined in (5) is diminished (the time to failure is shorted) and as a consequence,
defined in (5) is diminished (the time to failure is shorted) and as a consequence,  is overestimated.
is overestimated.
Statement 2: In multivariate ALT analysis, when significant variables 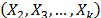 are added into
are added into 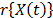 , the relation between the logarithm of the scale parameter
, the relation between the logarithm of the scale parameter 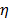 and
and 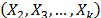 tends to be one, thus the corresponding sum square error is diminished increasing
tends to be one, thus the corresponding sum square error is diminished increasing 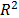 , and as a consequence,
, and as a consequence,  is overestimated.
is overestimated.
Considering these statements, firstly note that  is intrinsically related to the strength characteristics of the product; thus, if the levels of the significant variables
is intrinsically related to the strength characteristics of the product; thus, if the levels of the significant variables 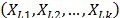 are selected in such that, for their higher effect combination, they do not generate a foolish failure mode (the effect of the level combinations is lower than the effect that reaches the destructive limits),
are selected in such that, for their higher effect combination, they do not generate a foolish failure mode (the effect of the level combinations is lower than the effect that reaches the destructive limits),  must be constant, and its value must represent the variance of the strength characteristic
must be constant, and its value must represent the variance of the strength characteristic 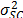 which in the estimation processes with constant over time and interval-valued variables is not used (or measured). And second, we can observe that in the estimation process, the shape parameter
which in the estimation processes with constant over time and interval-valued variables is not used (or measured). And second, we can observe that in the estimation process, the shape parameter  is determined by the variance of the logarithm of the lifetime data
is determined by the variance of the logarithm of the lifetime data 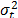 , the response variance
, the response variance 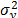 and the correlation coefficient
and the correlation coefficient 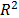 , and that neither of them represent
, and that neither of them represent 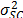 . Thus, due to the dependence of
. Thus, due to the dependence of  on
on 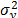 ,
, 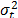 and
and 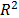 , adding significant variables (increases R2) and/or overstressing their levels (diminishes
, adding significant variables (increases R2) and/or overstressing their levels (diminishes 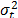 ) always overestimates
) always overestimates  as in the following section.
as in the following section.
4. Statistical analysis
Let us first show that  is completely determined by
is completely determined by 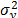 ,
, 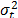 and
and 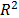 . To see this, let us use the Weibull reliability function given by
. To see this, let us use the Weibull reliability function given by
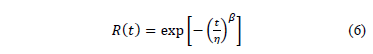
Which in linear form is given by
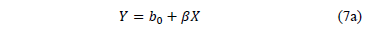
Where 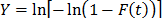 ,
, 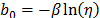 ,
, 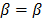 ,
, 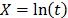 , and
, and 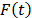 is the cumulative failure function of t given by
is the cumulative failure function of t given by 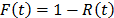 .
. 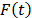 based on the median rank approach is estimated as [14].
based on the median rank approach is estimated as [14].
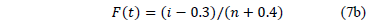
For another possible approximation of F(t), see [3], [4] and [21]. On the other hand, observe from (7a) that  is a critical parameter (see [10] and [16] sec. 2.3) and thus, the analysis depends on the accuracy by which it is estimated. Also, observe that (7b) is in function of the sample size n and that for
is a critical parameter (see [10] and [16] sec. 2.3) and thus, the analysis depends on the accuracy by which it is estimated. Also, observe that (7b) is in function of the sample size n and that for 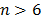 the F(t) percentile is greater than 90% [2]. Regardless of this, note that
the F(t) percentile is greater than 90% [2]. Regardless of this, note that 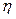 represents the 0.367879 reliability percentile which corresponds to
represents the 0.367879 reliability percentile which corresponds to 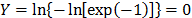 implying from (7a) that for center response Y
implying from (7a) that for center response Y
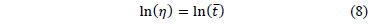
Thus, under multiple linear regression the coefficients of (7a) are estimated as
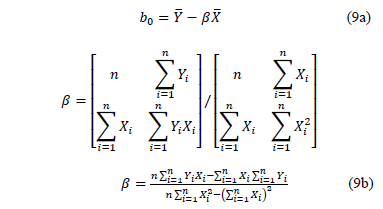
From (9b) observe that its denominator is the variance of the logarithm of the lifetime data defined in (5), which in terms of the covariates is given by.
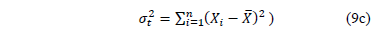
On the other hand, the goodness of fit of the polynomial given in (7a) is performed by the anova analysis where its sources of variation are
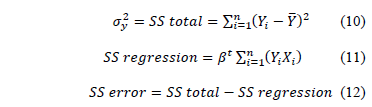
The goodness of fit index is given by
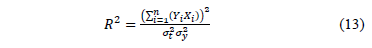
Finally from (9c), (10), (11) and (13),  is given by
is given by
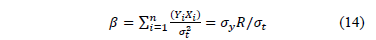
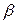 On the other hand, to see that increasing (or decreasing)
On the other hand, to see that increasing (or decreasing) 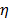 affects
affects  as in Statement1, note from (8) that increasing (or decreasing)
as in Statement1, note from (8) that increasing (or decreasing) 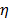 is equivalent to increasing (or decreasing)
is equivalent to increasing (or decreasing) 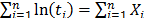 in (9b). That is to say, shortening the time in which the lifetime occurs, decreases their variance
in (9b). That is to say, shortening the time in which the lifetime occurs, decreases their variance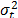 and thus, according to (14), is overestimated.
and thus, according to (14), is overestimated.
In the case of Statement 2, from (11) to (14), it is clear that although the levels of the variables are not stressed, by adding significant variables, since 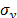 and
and 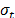 , are fixed as in (5), then in (14)
, are fixed as in (5), then in (14) 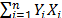 is increased, and as a consequence,
is increased, and as a consequence,  is always overestimated.
is always overestimated.
5. Proposed Method
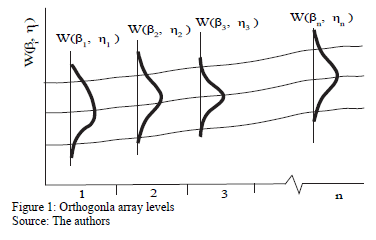
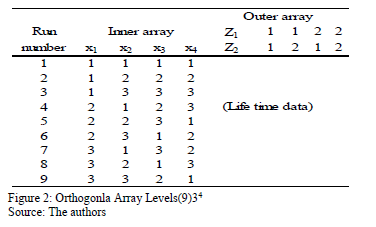
To see numerically that  is overestimated as in section 4, first note that each combination of the variables, as in Fig. 1, presents its own Weibull family, and that data are gathered by using a replicated experiment design DOE as presented in Fig. 2 (see [15] and [20] Chapter 13).
is overestimated as in section 4, first note that each combination of the variables, as in Fig. 1, presents its own Weibull family, and that data are gathered by using a replicated experiment design DOE as presented in Fig. 2 (see [15] and [20] Chapter 13).
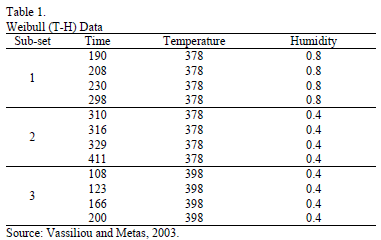
Second, to illustrate this, let us use the DOE data from Table 1, which corresponds to twelve electronic devices. Data were published by [17] p.11.
From these data, the Weibull/(T-H) parameters defined in (3), by using ML are 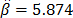 ,
, 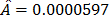 ,
, 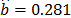 and
and 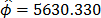 (the ALTA Pro software was used). In addition, observe that although in Table 1 there are three level combinations among the variables, which as a consequence lead to three Weibull families in this DOE, regardless of this, in the standard approach [eq. (3)], only one shape parameter
(the ALTA Pro software was used). In addition, observe that although in Table 1 there are three level combinations among the variables, which as a consequence lead to three Weibull families in this DOE, regardless of this, in the standard approach [eq. (3)], only one shape parameter 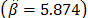 was estimated.
was estimated.
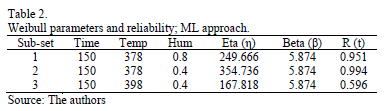
Thus, it is not representative of the whole set of data. To see this, in Table 2, the scale and shape parameters 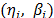 , estimated by ML, and their associated reliability
, estimated by ML, and their associated reliability 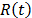 for t=150 are given.
for t=150 are given.
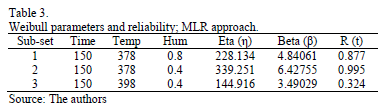
In order to compare the standard results of Table 2, with those found in the DOE, Table 3 presents the Weibull family and R(t) for each DOE combination, using (8) and (9b) with centered response (Y).
By comparing these results, we observe that the estimated 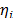 in Table 2, in contrast to the estimated
in Table 2, in contrast to the estimated 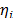 from Table 3, does not represent the expected 0.367879 percentile as defined in (8). And that
from Table 3, does not represent the expected 0.367879 percentile as defined in (8). And that 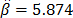 does not represent the shape parameter of the levels found in the DOE. Thus the proposed method to avoid this issue, using MLR, is as in the following section.
does not represent the shape parameter of the levels found in the DOE. Thus the proposed method to avoid this issue, using MLR, is as in the following section.
5.1. Regression approach for statement 1.
In ALT with one interval valued and constant over time variables, as is the case of Weibull/Arrhenius, Weibull/Inverse power law and Weibull/Eyring, it is possible to estimate their parameters by applying (8), (9a) and (9b) by following the next steps.
Step 1. For each replicated level of the stress variable (We must have almost 4 replicates, although 10 are recommended), determine the corresponding  and
and 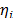 parameters by using (7a), (8), (9a) y (9b). (In this one variable approach,
parameters by using (7a), (8), (9a) y (9b). (In this one variable approach,  is generally constant). If
is generally constant). If  is not constant, proceed as in section 5.2.
is not constant, proceed as in section 5.2.
Step 2. Take the effect of the corresponding linear transformation (see next section) of the time/stress model 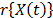 defined in (1) as
defined in (1) as 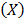 (e.g. in Arrhenius
(e.g. in Arrhenius 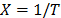 ) and the corresponding logarithm of the scale parameter
) and the corresponding logarithm of the scale parameter 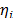 of the i-th level of the variable estimated in step 1 as
of the i-th level of the variable estimated in step 1 as 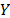
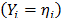 .
.
Step 3. Using (9a) and (9b), estimate by regression between the variables 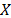 and
and 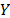 defined in step 2, the parameters of the life/stress model
defined in step 2, the parameters of the life/stress model 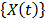 .
.
Note: In the Eyring case, do not forget to subtract the logarithm of the reciprocal of the temperature 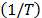 from the logarithm of
from the logarithm of 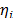 before you perform the regression.
before you perform the regression.
Step 4. Using the regression parameters of 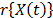 estimated in step 3, estimate the logarithm of
estimated in step 3, estimate the logarithm of 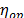 for the operational (or desired) level (see next section). Finally, form the Weibull family of the operational (or desired) level W(
for the operational (or desired) level (see next section). Finally, form the Weibull family of the operational (or desired) level W(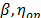 ) with the shape parameters estimated in step1 and the scale parameter estimated in this step. And with these Weibull parameters, determine the desired reliability indexes.
) with the shape parameters estimated in step1 and the scale parameter estimated in this step. And with these Weibull parameters, determine the desired reliability indexes.
5.1.1 Let us exemplify the above methodology, through the Weibull/Arrhenius and Weibull/Eyring relationship, which are parametrized as in (1). In the case of Arrhenius, the infinitesimal characteristic (see [18]) is given by 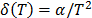 , thus the primitive (integral)
, thus the primitive (integral) 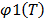 of
of 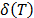 , is given by
, is given by 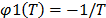 . Since
. Since 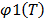 shows the form in which the variable affects the time, in the Arrhenius model the effect is
shows the form in which the variable affects the time, in the Arrhenius model the effect is 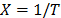 (see step 2 of section 5.1). Thus from (1) and (4), the Arrhenius model is given by: (for details see [1], Chapter 5).
(see step 2 of section 5.1). Thus from (1) and (4), the Arrhenius model is given by: (for details see [1], Chapter 5).

In (15a), 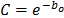 and
and 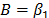 are the parameters to be estimated, and T is the absolute temperature (Kelvin). The linear form of (15a) is given by
are the parameters to be estimated, and T is the absolute temperature (Kelvin). The linear form of (15a) is given by
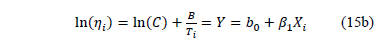
Using (15a) the Weibull/Arrhenius pdf is given by
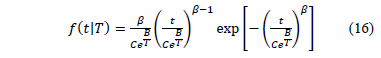
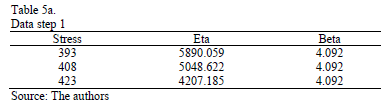
As a numerical application, consider the data in Table 4. Data were published by [17]. The Weibull parameters of step 1 are given in Table 5a. The effect for step 2, 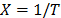 and
and 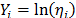 are given in Table 5b.
are given in Table 5b.
The Weibull/Arrhenius parameters of step 3 using Minitab® and data of Table 5b, are 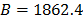 and
and 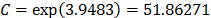 with
with 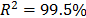 . Finally, by using these parameters, the Weibull family mentioned in step 4, for a level of 323K is
. Finally, by using these parameters, the Weibull family mentioned in step 4, for a level of 323K is 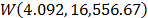 .
.
5.1.2 In the case of the Weibull/Eyring relationship the infinitesimal characteristic is given by 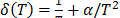 , with primitive
, with primitive 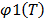 of
of 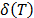 , given by
, given by 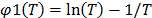 , thus
, thus 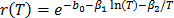 . This formulation with
. This formulation with 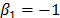 is used in the Eyring model when the temperature is used. The Eyring model is given by:
is used in the Eyring model when the temperature is used. The Eyring model is given by:
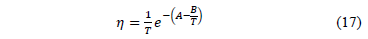
In (17), 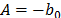 and
and 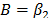 are parameters to be estimated and T is the absolute temperature. The linear relationship of (17) is
are parameters to be estimated and T is the absolute temperature. The linear relationship of (17) is
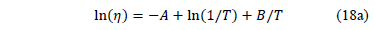
And the linear relationship used to estimate the parameters is given by
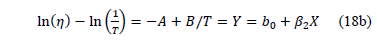
The Weibull/Eyring pdf using (17) is
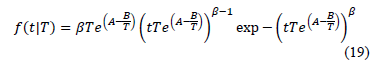
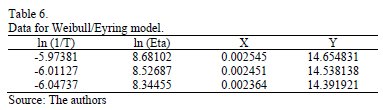
Using data of Table 4, the Weibull/Eyring parameters of step 3 using Minitab® with data of Table 6, are 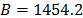 and
and 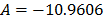 with
with 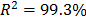 . By using these parameters the Weibull family mentioned in step 4, for a level of 323K is
. By using these parameters the Weibull family mentioned in step 4, for a level of 323K is 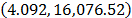 .
.
Finally, for the one variable case, when the shape parameter is not constant for all the stress levels proceed as in the multivariate case of the following section.
5.2. Regression approach for statement 2.
For the multivariate ALT analysis, as in Fig. 1, each covariate combination presents its own Weibull family. Thus, because in the standard ALT analysis, the estimated  value does not represent the whole set of data, in MLR, we propose to estimate the Weibull/life/stress parameters through the following steps.
value does not represent the whole set of data, in MLR, we propose to estimate the Weibull/life/stress parameters through the following steps.
Step 1. For each replicated combination level of the stress variables (We must have almost 4 replicates; 10 is recommended; see comment below eq. (7b)), determine the corresponding Weibull family 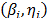 . This could be performed by ML, but MLR is recommended. (ML is a biased estimator and n is small).
. This could be performed by ML, but MLR is recommended. (ML is a biased estimator and n is small).
Step 2. Take the effect of the corresponding linear transformation of the variables as the independent variables 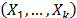 and the corresponding logarithm of the scale parameter
and the corresponding logarithm of the scale parameter 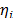 of the i-th Weibull family of step1 as the dependent variable
of the i-th Weibull family of step1 as the dependent variable 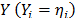 .
.
Step 3. Estimate the parameters of the life/stress model 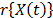 by regression between the set of variables
by regression between the set of variables 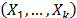 and
and 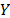 defined in step 2. If there are not enough degrees of freedom to perform the analysis, proceed as follows.
defined in step 2. If there are not enough degrees of freedom to perform the analysis, proceed as follows.
a) Estimate a vector 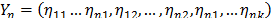 by reordering (7a) as
by reordering (7a) as
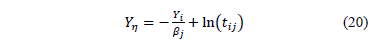
Estimate the parameters of 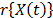 by performing a regression between
by performing a regression between 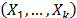 and
and 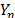 . In (20),
. In (20), 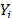 is as in (7b), and
is as in (7b), and 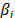 and
and 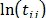 are the shape parameter and the logarithm of the lifetime data of the i-th Weibull families of step 1.
are the shape parameter and the logarithm of the lifetime data of the i-th Weibull families of step 1.
b) Based on (5) and on the fact that 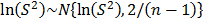 where
where 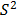 is the sample variance of the lifetime data, form the logarithm vector
is the sample variance of the lifetime data, form the logarithm vector
 where
where 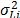 is the variance of the i-th level defined in (9c) and n is the number of replicates of the i-th level of step1.
is the variance of the i-th level defined in (9c) and n is the number of replicates of the i-th level of step1.
c) Take the inverse of the effect of the covariates of step 2, as the independent variables 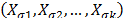 and
and 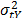 as the response variable and perform a regression between
as the response variable and perform a regression between 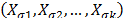 and
and 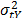 .
.
Observe that 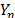 and
and 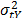 are vectors for the complete DOE data (or families).
are vectors for the complete DOE data (or families).
Step 4. Using the regression parameters of 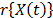 estimated in step 3-a), estimate the scale parameter
estimated in step 3-a), estimate the scale parameter 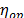 for the operational level by applying (4). By using the regression parameters of step 3-b), estimate the value of
for the operational level by applying (4). By using the regression parameters of step 3-b), estimate the value of 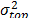 of the operational level, and by applying (14), with
of the operational level, and by applying (14), with 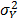 of step 1 and a desired
of step 1 and a desired 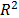 index, estimate the corresponding
index, estimate the corresponding 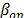 value.
value. 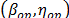 are the parameters of the Weibull family of the desired stress level and they could be used to determine any desired reliability index. Observe that the estimation of
are the parameters of the Weibull family of the desired stress level and they could be used to determine any desired reliability index. Observe that the estimation of 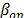 using (14) is robust (almost insensible) to the selected
using (14) is robust (almost insensible) to the selected 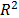 index.
index.
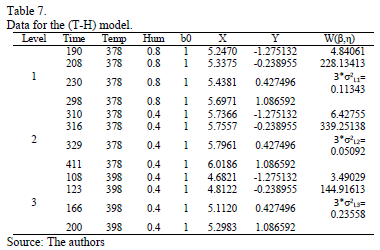
As a numerical application consider the data in Table 7. Data were published in [17].
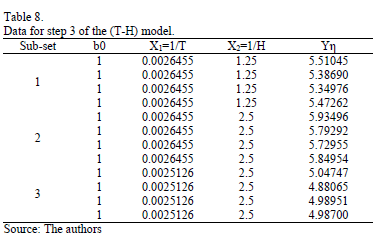
On the other hand, data of step 3 using (20) are given in Table 8. By using Minitab, the parameters of W(T-H) model by regression between 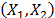 and
and 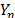 are
are 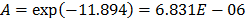 ,
, 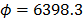 , and
, and 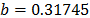 with
with 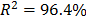 . The parameters of the regression between
. The parameters of the regression between 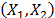 and
and 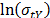 are
are 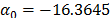 ,
, 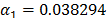 and
and 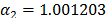 with
with 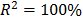 . To show the method, suppose that the operational level is
. To show the method, suppose that the operational level is 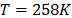 with
with 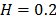 , then, by using the above parameters as in step 4,
, then, by using the above parameters as in step 4, 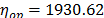 , and by taking
, and by taking 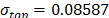 ,
, 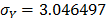 and
and 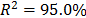 ,
, 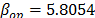 . Thus, the operational Weibull family is
. Thus, the operational Weibull family is 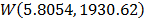 .
.
On the other hand, the ML parameters using the ALTA routine are 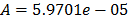 ,
, 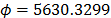 ,
, 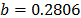 with
with 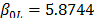 and
and 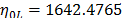 . With operational Weibull Family given by
. With operational Weibull Family given by 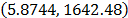 . A comparison of the Weibull parameters and reliability index of the ML and the proposed Method is given in Table 9.
. A comparison of the Weibull parameters and reliability index of the ML and the proposed Method is given in Table 9.
In Table 9, we can see that the shape parameter is not representative of the observed Weibull families as it is in the proposed method. The same occurs with the estimated reliability. In particular, it is important to note that the proposed method is based on the observed variance and thus it is directly related to the operational factors of the process.
6. Conclusions
In Weibull multivariate ALT analysis, each combination of the significant variables presents its own behavior, thus the standard approach of estimating only one shape parameter to represent all the Weibull families is suboptimal. Since  depends on
depends on 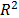 , which increases when variables are added to the analysis, in the multivariate case
, which increases when variables are added to the analysis, in the multivariate case  is always overestimated. Clearly, since the change in the scale parameter
is always overestimated. Clearly, since the change in the scale parameter 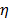 is reflected in
is reflected in 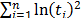 , thus the proposed method could easily be generalized to the right censured case by reflecting the censured data on
, thus the proposed method could easily be generalized to the right censured case by reflecting the censured data on 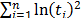 and by substituting
and by substituting 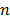 for
for 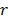 in (9b) where
in (9b) where 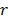 is the number of failure. Although the proposed method depends greatly on the accuracy in which
is the number of failure. Although the proposed method depends greatly on the accuracy in which 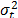 is estimated, because
is estimated, because 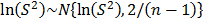 stabilize the variance as defined in step 3-b, the proposed method could be considered robust for this issue. It is important to mention that
stabilize the variance as defined in step 3-b, the proposed method could be considered robust for this issue. It is important to mention that  in (14) is not highly sensitive to the selected
in (14) is not highly sensitive to the selected 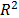 index. Knowing (14), it seems to be possible to generalize the proposed method to the ML approach by formulating a log-likelihood function based on the b values of the Weibull families, but more research must be undertaken. Since the shape parameter
index. Knowing (14), it seems to be possible to generalize the proposed method to the ML approach by formulating a log-likelihood function based on the b values of the Weibull families, but more research must be undertaken. Since the shape parameter  is inversely related to
is inversely related to 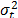 , and because
, and because 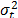 is the standard deviation of the lognormal distribution, which presents a flexible behavior and similar analysis to the Weibull distribution [11], it seems to be possible to extend the present method to the lognormal analysis. On the other hand, although the proposed method is practical and its application could easily be performed by using a standard software routine, as Minitab does, a more detailed method could be proposed by using a copula to modeling in joint form the Weibull families behavior, but because the Weibull distribution is determined by an non-homogeneous Poison processes [7] and its convolutions do not have a closed form [12], more research must be undertaken.
is the standard deviation of the lognormal distribution, which presents a flexible behavior and similar analysis to the Weibull distribution [11], it seems to be possible to extend the present method to the lognormal analysis. On the other hand, although the proposed method is practical and its application could easily be performed by using a standard software routine, as Minitab does, a more detailed method could be proposed by using a copula to modeling in joint form the Weibull families behavior, but because the Weibull distribution is determined by an non-homogeneous Poison processes [7] and its convolutions do not have a closed form [12], more research must be undertaken.
References
[1] Bagdonaviĉius, V. and Nikulin, M., Accelerated life models, modeling and statistical analysis, Florida: Chapman and Hall/CRC, 2002. [ Links ]
[2] Bertsche, B., Reliability and automotive and mechanical engineering, Berlin: Springer, 2008. [ Links ]
[3] Cook, N. J., Comments on plotting positions in extreme value analysis. J. Appl. Meteor., 50 (1), pp. 255-266, 2011. DOI: 10.1175/2010JAMC2316.1. [ Links ]
[4] Cook, N. J., Rebuttal of problems in the extreme value analysis. Structural Safety., 34 (1), pp. 418-423, 2012. DOI: 10.1016/j.strusafe.2011.08.002. [ Links ]
[5] Cox, D.R. and Oakes, D., Analysis of survival data, Florida: Chapman and Hall/CRC, 1984. [ Links ]
[6] Escobar, L.A. and Meeker, W.Q., A review of accelerated test models. Statistical Science, 21 (4), pp. 552-577, 2006. DOI: 10.1214/088342306000000321. [ Links ]
[7] Jun-Wu, Y., Guo-Liang, T. and Man-Lai, T., Predictive analysis for nonhomogeneous poisson process with power law using Bayesian approach. Computational Statistics and Data Analysis., 51, pp. 4254-4268, 2007. DOI: 10.1016/j.csda.2006.05.010. [ Links ]
[8] Nelson, W.B., Applied life data analysis, New York: John Wiley & Sons, 1985. [ Links ]
[9] Nelson, W.B., Accelerated testing statistical models, test plans and data analysis, New York: John Wiley & Sons, 2004. [ Links ]
[10] Nicholls, D. and Lein, P., Weibayes testing: What is the impact if assumed beta is incorrect? Reliability and Maintainability Symposium, RAMS Annual, 2009. pp. 37-42. DOI: 10.1109/RAMS.2009.4914646 [ Links ]
[11] Manotas, E., Yañez, S., Lopera, C. and Jaramillo, M., Estudio del efecto de la dependencia en la estimación de la confiabilidad de un sistema con dos modos de falla concurrentes. DYNA, 75 (154), pp. 29-38, 2007. [ Links ]
[12] McShane, B., Adrian, M., Bradlow, E. and Fader, P., Count models based on Weibull interarrival times. Journal of Business and Economic Statistics, 26 (3), pp. 369-378, 2008. DOI: 10.1198/073500107000000278. [ Links ]
[13] Meeker, W.Q. and Escobar, L.A., Statistical methods for reliability data. New York: John Wiley & Sons, 2014. [ Links ]
[14] Mischke, C.R., A distribution-independent plotting rule for ordered failures. Journal of Mechanical Design, 104 (3), pp. 593-597, 1979. DOI: 10.1115/1.3256391. [ Links ]
[15] Montgomery, D.C., Diseño y análisis de experimentos. México, D.F.: Limusa Wiley, 2004. [ Links ]
[16] Rinne, H., The Weibull distribution a handbook. Florida: CRC press, 2009. [ Links ]
[17] Vassiliou, P. and Metas, A., Application of Quantitative Accelerated Life Models on Load Sharing Redundancy. Reliability and Maintainability, 2004 Annual Symposium - RAMS, pp. 293-296, DOI: 10.1109/RAMS.2004.1285463 [ Links ]
[18] Viertl, R., Statistical methods in accelerated life testing. Göttingen: Vandenhoeck & Ruprecht, 1988. [ Links ]
[19] Weibull, W., A statistical theory of the strength of materials. Stockholm: Generalstabens litografiska anstalts förlag. 1939. [ Links ]
[20] Yang, K. and El-Haik, B., Design for six sigma: a roadmap for product development. New York: McGraw-Hill. 2003. [ Links ]
[21] Yu, G.H. and Huang, C.C., A distribution free plotting position. Stochastic environmental research and risk assessment, 15 (6), pp. 462-476, 2001. DOI: 10.1007/s004770100083. [ Links ]
M.R. Piña-Monarrez, is a Researcher-Professor at the Autonomous University of Ciudad Juarez, Mexico. He completed his PhD degree in Science in Industrial Engineering in 2006 at the Technological Institute of Ciudad Juarez, Mexico. He had conducted research on system design methods including robust design, design of experiments, linear regression, reliability and multivariate process control. He is member of the National Research System (SNI-1), of the National Council of Science and Technology (CONACYT) in Mexico.
C.A. Ávila-Chavez, is a PhD student on the Science in Engineering Doctoral Program (DOCI), at the Autonomous University of Ciudad Juarez, Mexico. He completed his MSc. degree in Science in Industrial Engineering in 2011 at the Technological Institute of Ciudad Juarez, Mexico. His research is based on Accelerated lifetime and Weibull analysis.
C.D. Márquez-Luevano, is a reliability engineering at the Stoneridge Electronics North America El Paso Texas, USA. He completed his MSc. degree in Industrial Engineering in 2013 at the Autonomous University of Ciudad Juarez, Mexico. His research studies on reliability focus on random vibration and Weibull analysis.