Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.192 Medellín July/Aug. 2015
https://doi.org/10.15446/dyna.v82n192.48569
DOI: http://dx.doi.org/10.15446/dyna.v82n192.48569
Voltage regulation in a power inverter using a quasi-sliding control technique
Regulación de tensión en un inversor de potencia usando técnica de control cuasi deslizante
Nicolás Toro-García a, Yeison Alberto Garcés-Gómez b & Fredy Edimer Hoyos-Velasco c
a, b Facultad de Ingeniería y Arquitectura, Universidad Nacional de Colombia, Manizales, Colombia. ntoroga@unal.edu.co, yagarsesg@unal.edu.co
c Escuela de Física, Universidad Nacional de Colombia, Medellín, Colombia. fehoyosve@unal.edu.co
Received: October 07th, 2014. Received in revised form: February 12th, 2015. Accepted: July 02nd, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
This paper shows the behavior of a three-phase power converter with resistive load using a quasi-sliding and a chaos control techniques for output voltage regulation. Controller is designed using Zero Average Dynamic (ZAD) and Fixed Point Inducting Control (FPIC) techniques. Designs have been tested in a Rapid Control Prototyping (RCP) system based on Digital Signal Processing (DSP) for dSPACE platform. Bifurcation diagrams show the robustness of the system. Chaos detection is a signal processing method in the time domain, and has power quality phenomena detection applications. Results show that the phase voltage in the load has sinusoidal performance when it is controlled with these techniques. When delay effects are considered, experimental and numerical results match in both of stable and transition to chaos zones.
Keywords: Power measurement, Power quality, Power electronics, Complexity theory, Chaos, Power Inverter.
Resumen
Este documento presenta el desempeño de un inversor de potencia con carga resistiva usando una técnica de control cuasi deslizante y una técnica de control de caos para la regulación de la tensión de salida. El controlador se diseño usando técnicas de Dinámica de Promedio Cero (ZAD) y Punto Fijo de Control de Inducción (FPIC). Los diseños han sido probados en un sistema de Prototipado Rápido de Control (RCP) basado en un Procesador Digital de Señales (DSP) para la plataforma dSPACE. Los diagramas de bifurcaciones muestran la solides del sistema. La detección de caos se realiza por un método de procesamiento de señales en el dominio del tiempo, y tiene aplicaciones en detección de fenómenos de calidad de la potencia. Los resultados muestran que la tensión de fase de la carga tiene desempeño sinusoidal cuando se controla con las técnicas mencionadas. Cuando se consideran los efectos de retraso, los resultados simulados y experimentales coinciden en ambos casos en zonas estables y de transición a caos.
Palabras clave: Medida de potencia, Calidad de la Potencia, Electrónica de Potencia, Teoría Compleja, Caos, Inversor de Potencia.
1. Introduction
The study of variable structure systems uses bifurcation theory in order to determine the conditions in parameter values which generate stability changes, periodicity and chaotic dynamics in the system, and which allow us to define safe and stable operation zones. Knowledge of these operation ranges let us avoid the presence of non-desired phenomena such as auto-sustained oscillations, chaos, and evolution to other operation regimes, among others.
Control action required for three-phase loads is implemented usually by power electronic circuits based on switches. For this reason, controlled commuted system with three-phase-load (Resistive) becomes a variable structure system defined by non-smooth differential equations in which a complete theoretical framework does not exist yet allows its study [1] since its theoretical and numerical analysis represents an extremely difficult problem [3]. In this sense, non-smooth transitions occur when a cycle interacts with a boundary of discontinuity in the phase space in a non-generic way, causing periodic additions or sudden chaos transitions [4]. One of the most relevant aspects in the bifurcation analysis of non-smooth systems is the absence of the double periodic sequences that are observed in smooth systems [3]. Due to characteristic behavior of non-smooth systems, in many cases, it is not possible to apply analysis techniques for smooth systems without modifications or adequate adjustments [1].
Converters use power electronics for efficient transformation and rational use of electricity from the generation sources to its industrial and commercial use. It has been estimated that 90% of electrical energy is processed through power converters before the final use [5]. Power converters must provide a certain level of output voltage, either in task regulation or tracking, and they must be able to reject changes in load and primary supply voltage levels. A complete and detailed analysis of the operation and configuration of different power converters can be found in [6, 7]. One of the most desirable qualities in these devices is efficiency in the performance by using switching devices generating the desired output with low power consumption.
In general, the deterioration of power quality is due to non-stationary disturbances (voltage sags, voltage swells, impulses, among others) and also due to stationary disturbances (harmonic distortion, unbalance and flicker) [8-11]. In addition, the chaotic dynamics in the system under study generate non-periodic solution currents that are reflected on the source side, affecting other sensitive loads connected to the point of common coupling.
Controller designed in this work combines Zero Average Dynamics (ZAD) and Fixed Point Inducting Controller (FPIC) strategies, which have been reported in [18]. Design corresponds to a three-phase low power inverter (1500 W) with a three phase resistive load using a dSPACE platform for the control. Numerical and experimental bifurcations are obtained for the ZAD-FPIC-controller [22-24], by changing the parameter values. Obtained numerical and experimental bifurcation diagrams match. Development and application of the FPIC control technique are presented in [14,15,17,18]. This technique allows the stabilization of unstable orbits in a simple way.
This paper is organized as follows. Section 2 describes the proposed system. Section 3 describes the mathematical model of the system. Section 4 describes the control techniques. Section 5 presents the obtained results, and finally, section 6 presents the conclusion.
2. Proposed system
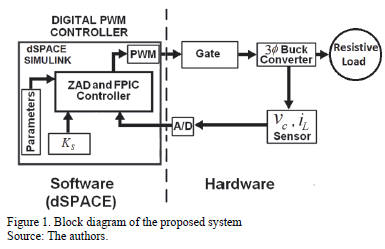
Fig. 1 shows the block diagram of the system under study. This system is divided into two major subgroups, hardware and software. Hardware includes electrical circuits and electronic devices, and software includes signals acquisition and implementation of control techniques. The software is implemented in a dSPACE platform.
Hardware is composed of a Three-phase power converter with resistive load, which is rated to 1500W, 600 V DC and 20 A DC. For the measure of variables, 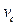 (capacitor voltage), a series resistance was used and for the measurement of
(capacitor voltage), a series resistance was used and for the measurement of 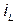 (inductor currents) HX10P/SP2 current sensors were used. Converter switches were driven by PWM outputs of the controller card; these signals are coupled via fast optocouplers (6N137).
(inductor currents) HX10P/SP2 current sensors were used. Converter switches were driven by PWM outputs of the controller card; these signals are coupled via fast optocouplers (6N137).
Software is developed using the control and development card dSPACE DS1104, where ZAD and FPIC control techniques are implemented. The sampling rate for all variables is set to 4 kHz. The state variables 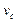 and
and 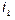 are stored at 12 bits; the duty cycle (d) is handled at 10 bits. Parameters of buck converter (
are stored at 12 bits; the duty cycle (d) is handled at 10 bits. Parameters of buck converter (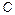 ,
,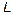 ,
,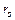 ,
,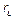 ) and ZAD-FPIC-controller (
) and ZAD-FPIC-controller (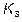 ,
,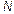 ,
,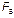 ,
,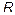 ) are entered to the control block by the user, as constant parameters.
) are entered to the control block by the user, as constant parameters. 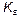 is the bifurcation parameter. For each sample the controller calculates in real time the duty cycle and the equivalent PWM signal to control the gate.
is the bifurcation parameter. For each sample the controller calculates in real time the duty cycle and the equivalent PWM signal to control the gate.
3. Mathematical model
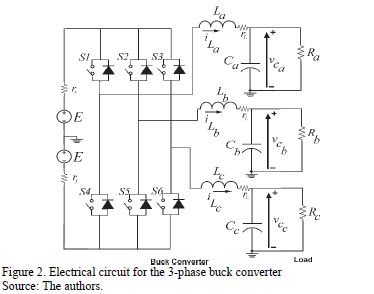
Fig. 2 shows a basic diagram of the system. Buck power converter is used to feed the resistive load. Eq. (1) is obtained for the system model.
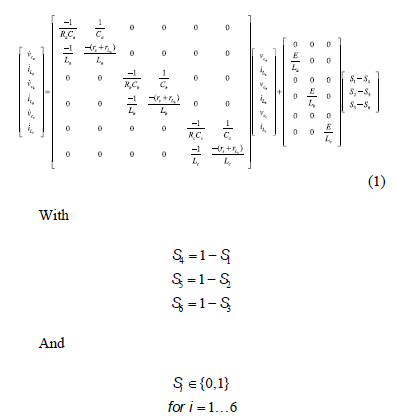
This equation can be expressed in a compact form as:

where the state variables are:
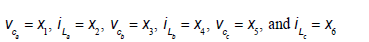
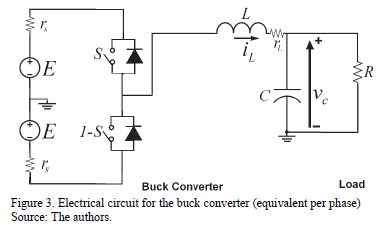
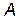 is a block diagonal matrix, so that the system consists of three uncoupled subsystems that may be treated independently. Fig. 3 shows the equivalent circuit per phase.
is a block diagonal matrix, so that the system consists of three uncoupled subsystems that may be treated independently. Fig. 3 shows the equivalent circuit per phase.
3.1. Derivation of the discrete time iterative map of the converter
The inherent piecewise switched operation converters implies a multi-topological mode in which one particular circuit topology describes the system for a particular interval of time. The first step in the analysis of multi-topological circuit is to write down the state equations, which describes the individual switched circuits. For converters operating in the continuous conduction mode, two switched circuits can be identified. When the switch is ON, it is described by Eq. (3); when the switch is OFF, it is described by Eq. (4).
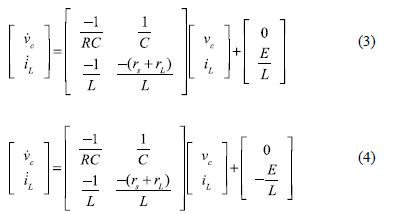
State variables are the capacitor voltage (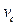 ) and the inductor current (
) and the inductor current (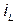 ). These equations can be expressed in a compact form as
). These equations can be expressed in a compact form as 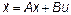 with
with 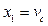 and
and 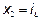 .
. 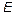 Denotes the converter power supply and depending on the control pulse voltage
Denotes the converter power supply and depending on the control pulse voltage 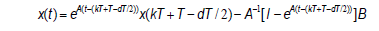 or
or 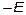 is injected to the system through a PWM signal.
is injected to the system through a PWM signal.
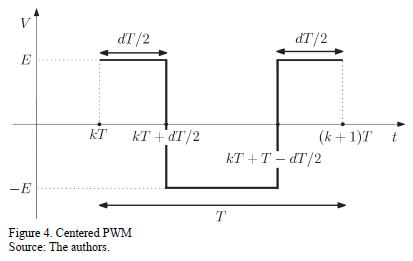
By considering continuous conduction mode (CCM) and according to centered PWM (Fig. 4), the control signal is defined as follows:
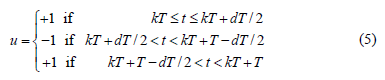
Solution of the system (3) for 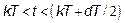 is given by:
is given by:
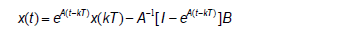
Solution of the system (4) for 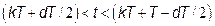 is given by:
is given by:
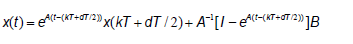
where
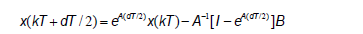
The solution of the system (3) for 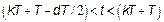 is given by:
is given by:
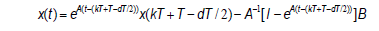
where
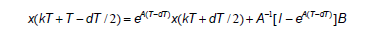
General solution of the system for 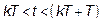 is given by:
is given by:
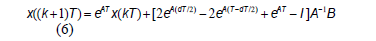
where 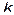 represents the
represents the 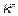 iteration,
iteration, 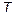 is the sampling period and
is the sampling period and 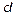 is the duty cycle Eq. (6) is the discrete-time state equation for the buck converter. In much of the literature, the terms iterative map, iterative function and Poincaré map have been used synonymically with discrete-time state equation.
is the duty cycle Eq. (6) is the discrete-time state equation for the buck converter. In much of the literature, the terms iterative map, iterative function and Poincaré map have been used synonymically with discrete-time state equation.
4. Control strategies
The control strategies presented in this section are developed for the per phase equivalent circuit. So for the three phase system the control must be applied for each phase independently, taking into account that the reference voltage will be phase shifted according to the corresponding circuit phase.
4.1. Derivation of the discrete time iterative map of the converter
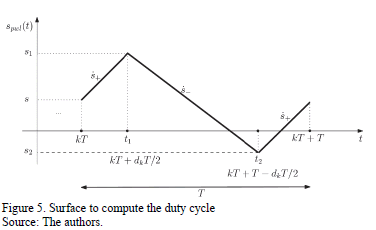
As reported in [19-[21], one of the possibilities for computing the duty cycle is to define a surface and to force it to be zero in each iteration. The surface per phase is defined as a piecewise-linear function as (Fig. 5) given by:
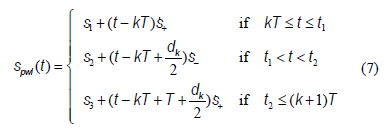
where the variables are described in (8) with 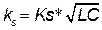 a positive constant.
a positive constant.
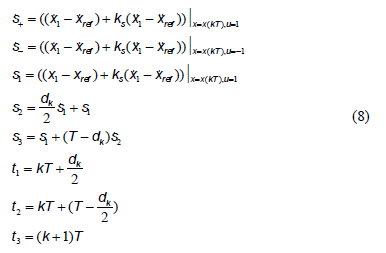
The 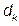 satisfying zero average requirements is:
satisfying zero average requirements is:

From (3), (4) and (8) we obtain:
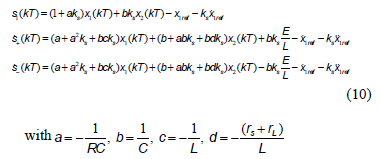
The duty cycle is given by (11).
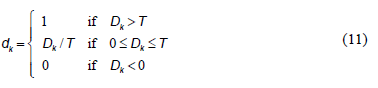
We have experimentally measured and noticed that there is a period of delay in the control action. In this case, the control action is taken from the data acquired in the past sampling time, and then we compute the duty cycle as:
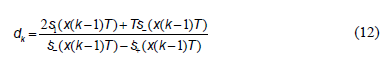
To apply this technique we need to measure the states at the beginning of each sampling time. To do this, we carry out a synchronization between the measured signals and the start of the PWM. This synchronization is performed using a trigger signal obtained from the PWM, which gives the command to the ADC converter for reading 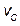 and
and 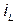 . On the other hand, we need to know the values of the parameters
. On the other hand, we need to know the values of the parameters 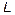 ,
, 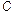 ,
, 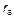 ,
, 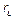 . In this case, we suppose that these parameters will be constant and measurable. The load
. In this case, we suppose that these parameters will be constant and measurable. The load 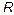 may be unknown and in this case must be estimated.
may be unknown and in this case must be estimated.
Taking into account the strategies FPIC and ZAD [22, 23], the new duty cycle is calculated as follow:

Where 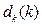 is calculated as (12) and
is calculated as (12) and 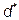 is the duty cycle calculated in steady state
is the duty cycle calculated in steady state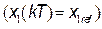 . From (9) we have:
. From (9) we have:
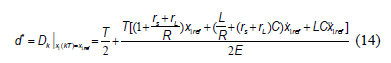
5. Numerical and experimental results
In this section numerical and experimental results are shown using 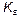 and
and 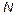 as bifurcation parameters, in addition the system behavior under frequency and voltage amplitude variations are illustrated graphically. Parameter values used in simulations and experiments are listed in Table 1; initially the reference voltage has a peak of 32V and 40Hz of frequency. For the simulation in SIMULINK model the fixed step size (fundamental sample time) in the configuration parameter was setting in
as bifurcation parameters, in addition the system behavior under frequency and voltage amplitude variations are illustrated graphically. Parameter values used in simulations and experiments are listed in Table 1; initially the reference voltage has a peak of 32V and 40Hz of frequency. For the simulation in SIMULINK model the fixed step size (fundamental sample time) in the configuration parameter was setting in 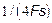 .
.
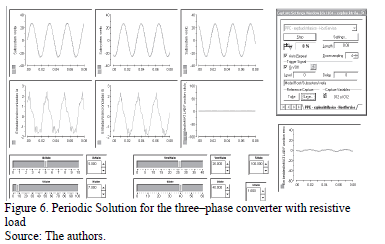
Figs. 6 and 7 show the experimental behavior for the Three-phase power converter, using the same parameters and controller, but with different initial conditions. Reference Voltages for phases a, b, c (upper signals); phase voltages (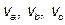 ) and phase currents (
) and phase currents (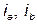 ) (middle signals) are shown in these Figures.
) (middle signals) are shown in these Figures.
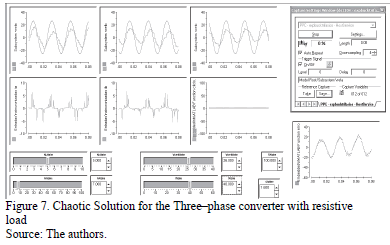
In Fig. 6 the system exhibits a periodic solution and in Fig.7 a chaotic solution. This fact shows the coexistence of attractors or solutions in the system. When the solution is periodic, the controlled voltage follows the voltage reference by the control action unlike the chaotic solution, where the output voltage is lower than the reference and it has an irregular fashion, in this regime the phase currents have a higher peak. Sometimes the system toggles between two solutions while it is running, this happens when the solution is near to the border of two regions of attraction.
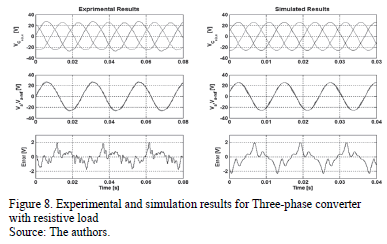
Results obtained in simulation and experiments for periodic solutions are shown in Fig. 8. The simulation was executed taking into account a 3T (0,75ms) delay in the duty cycle application. Under this condition simulation and experimental results match. Controlled voltage 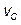 follows reference voltage for all phases with a maximum error of 2V.
follows reference voltage for all phases with a maximum error of 2V.
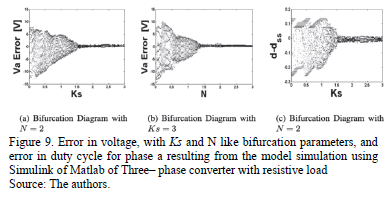
Fig. 9 shows the bifurcation diagrams for the output error and duty cycle of controlled system with KS and N like bifurcation parameters, obtained via model simulation using Simulink of Matlab. For 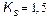 with
with 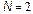 and
and 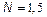 with
with 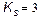 the system presents a qualitative behavior change. Before
the system presents a qualitative behavior change. Before 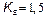 and
and 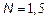 the system is in chaotic regime and after it is in stable regime. For constructing these diagrams, the simulation was running for 3 periods of reference voltage and the last 15 samples of output error are taken with initial conditions equal to zero; also a delay in duty cycle application of 3T.
the system is in chaotic regime and after it is in stable regime. For constructing these diagrams, the simulation was running for 3 periods of reference voltage and the last 15 samples of output error are taken with initial conditions equal to zero; also a delay in duty cycle application of 3T.
In the following the results of experiments are shown for buck power converter behavior when the voltage reference and voltage level vary.
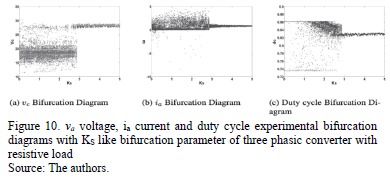
Fig.10 shows the bifurcation diagrams for the output error and duty cycle of the controlled system with 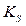 and N as bifurcation parameters, obtained experimentally. For
and N as bifurcation parameters, obtained experimentally. For 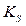 = 3 the system presents a qualitative behavior change. Before
= 3 the system presents a qualitative behavior change. Before 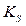 = 3 the system is in chaotic regime and after it is in stable regime. For constructing these diagrams, the experiment was run for 2 seconds for each value of
= 3 the system is in chaotic regime and after it is in stable regime. For constructing these diagrams, the experiment was run for 2 seconds for each value of 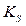 and samples were acquired every 50 milliseconds.
and samples were acquired every 50 milliseconds.
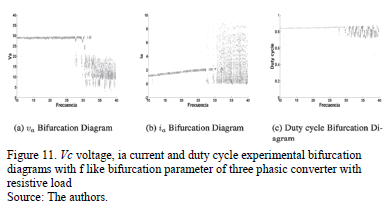
Fig. 11 shows the bifurcation diagrams for the 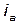 current,
current, 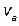 voltage and duty cycle of controlled system with f (frequency of voltage reference) like bifurcation parameter, obtained experimentally. For
voltage and duty cycle of controlled system with f (frequency of voltage reference) like bifurcation parameter, obtained experimentally. For 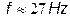 the system presents a qualitative behavior change. After
the system presents a qualitative behavior change. After 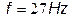 the system is in chaotic regime before its stable regime. For constructing these diagrams, the experiment was run for 2 seconds for each value of f and samples were acquired every 50 milliseconds. The phenomenon shown in Fig. 11 is caused by saturation of the inductor core in the LC filter; due to the fact that the core saturation and magnetic hysteresis not were simulated these phenomena are not present in simulations.
the system is in chaotic regime before its stable regime. For constructing these diagrams, the experiment was run for 2 seconds for each value of f and samples were acquired every 50 milliseconds. The phenomenon shown in Fig. 11 is caused by saturation of the inductor core in the LC filter; due to the fact that the core saturation and magnetic hysteresis not were simulated these phenomena are not present in simulations.
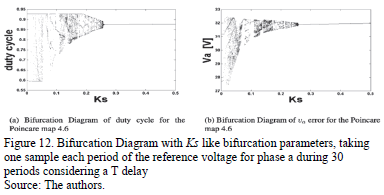
Fig. 12(a) shows the bifurcation diagram of duty cycle and Fig. 12(b) shows the bifurcation diagram of va for the Poincare map (6), both of which are numerical. Bifurcation diagrams were constructed taking the last 30 samples, each one for every period of reference voltage for phase a from the model (6) simulation using Matlab, while the system was running during 35 periods. The simulation was executed taking into account a single period (1T) of delay in the duty cycle application. In these Figures various regimes of operation can be appreciated: periodic windows, Chaos and periodic solutions.
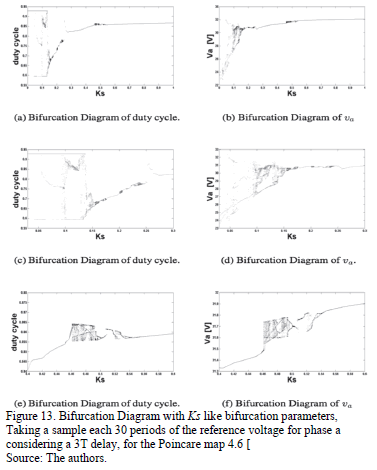
Fig. 13 shows the bifurcation diagram when 3T of delay is considered. Bifurcation diagrams are quite different for different delay.
Before analysis shows the effects of the delay time in the signal control applied to the power converter. Many complex phenomena arise as shown in Figs. 13(e) and 13(f) some of these are not smooth bifurcations, double period bifurcations, chaos and 1-periodic orbits.
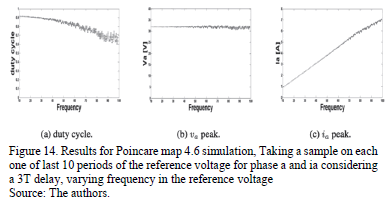
In order to analyze the effect of the variation of frequency and voltage level in the reference voltage, a simulation was carried out.
Results obtained varying the frequency of reference voltage are shown in Fig. 14. The Figs. 14(a), 14(b), 14(c) show the behavior of duty cycle, peak voltage and peak current in C and L respectively when the frequency voltage reference is varied in the Poincare map simulation. The amplitude of the output voltage does not drop significantly with the variation of frequency, but the current peak has a linear growth with frequency, showing a predominant capacitive effect. In this case the delay does not have a significant impact.
5. Conclusion
Control strategy ZAD-FPIC was designed and applied to a three-phase buck converter with resistive load. For this system, simulations and experiments were performed. The stability of the closed loop system was analyzed using bifurcation diagrams; stability and transitions to chaos were observed. It was demonstrated in an experimental way, that the delay effects have high importance in the ZAD strategy. Simulations and experiments match when delay effects were included and improve the quality of the waves with ZAD control. Thus, in the chaos zone, a power quality deterioration by non-periodical current and voltage waveforms was observed, but, when the control is performed the non-periodicity is eliminated.
Acknowledgments
This work was supported in part by the Universidad Nacional de Colombia, Manizales Branch, the Universidad Autonoma de Manizales and the Instituto Tecnológico de Antioquia.
The authors would like to thank the DIMA (Dirección de Investigaciones de la Sede Manizales) for their support throughout the projects "HERMES-19210 (Prototipo de controlador unificado de calidad de la energía con funciones de generación distribuida) y HERMES-19190 (Diseño y construcción de controladores de cargas y generadores para el laboratorio de energías renovables)."
References
[1] DiBernardo M. et al, Bifurcatios in nonsmooth dynamical systems,AMS Subject Classifications: 34A36, 34D08, 37D45, 37G15, 37N05, 37N20, May. 2006. [ Links ]
[2] DiBernardo M. et al, Piecewise-smooth dynamical systems: Theory and applications, Springer, New York, 2007. [ Links ]
[3] Zhusubaliyev, Z.T. and Mosekilde, E., Bifurcations and chaos in piecewise-smooth dynamical systems, World Scientific, series on Nonlinear sciencE, A, vol. 44, London. 2003. [ Links ]
[4] Kowalczyk, P. et al, Two-Parameter discontinuity-induced bifurcations of cycles: Classification and open problems, International Journal of Bifurcation and Chaos., 16 (3), PP. 601-6292006. DOI: 10.1142/S0218127406015015 [ Links ]
[5] Banerjee, S. and Verghese, G.C., Nonlinear phenomena in power electronics, IEEE Press. Piscataway, 2001. DOI: 10.1109/9780470545393 [ Links ]
[6] Mohan, N., Undeland, T. and Robbins, W., Power Electronics: Converters. Aplications and design, J. Wiley., 1995. [ Links ]
[7] Mohan, N., First Course on Power Electronics and drives, Mnpere, USA., 2003. [ Links ]
[8] Lin, T. and Domijan, A., On power quality indices and real time measurement, IEEE Trans. Power Del., 20 (4), pp. 2552-2562, 2005. DOI: 10.1109/TPWRD.2005.852333 [ Links ]
[9] Ferrero, A., Measuring electric power quality: Problems and perspectives, Measurement, 41 (2), pp.121-129, 2008, DOI: 10.1016/j.measurement.2006.03.004. DOI: 10.1016/j.measurement.2006.03.004 [ Links ]
[10] Salmerón, P., Herrera, R.S., Pérez, A. and Prieto, J., New distortion and unbalance indices based on power quality analyzer measurements, IEEE Trans. Power Del., 24 (2), 2009. [ Links ]
[11] Shin, Y.J., Powers, E.J., Grady, M. and Arapostathis, A., Power quality indices for transient disturbances, IEEE Trans. Power Del., 21 (1), 2006. [ Links ]
[12] Fossas, E. and Griñó, R. and Biel, D., Quasi-sliding control based on pulse width modulation. zero averaged dynamics and the L2 norm, advances in variable structure systems. Analysis. Integration and Applications (6th International Workshop on Variable Structure Systems (VSS'2000)., pp. 335-344, 2000. [ Links ]
[13] Angulo, F., Olivar, G. and Taborda, J.A., Continuation of periodic orbits in a ZAD-strategy controlled buck converter, Chaos. Solitons and Fractals., 38, pp. 348-363, 2008. DOI: 10.1016/j.chaos.2007.04.023 [ Links ]
[14] Angulo, F., Fossas, E. and Olivar, G., Transition from periodicity to chaos in a PWM controlled buck converter with ZAD strategy, Int. Journal of Bifurcations and Chaos., 15, pp. 3245-3264, 2005. DOI: 10.1142/S0218127405014015 [ Links ]
[15] Angulo., F., Análisis de la dinámica de convertidores electrónicos de potencia usando PWM basado en promediado cero de la dinámica del error (ZAD), Tesis, Universidad Politécnica de Cataluña, Cataluña., 2004. [ Links ]
[16] Taborda, J., Análisis de bifurcaciones en sistemas de segundo orden usando pwm y promediado cero de la dinámica del error, Tesis, Universidad Nacional de Colombia - Sede Manizales., Colombia, 2006. [ Links ]
[17] Angulo, F., Burgos J.E. and Olivar, G, Chaos stabilization with TDAS and FPIC in a buck converter controlled by lateral PWM and ZAD, In Proceedings: Mediterranean Conference on Control and Automation., July 2007. [ Links ]
[18] Angulo, F., Olivar, G., Taborda, J. and Hoyos, F., Nonsmooth dynamics and FPIC chaos control in a DC-DC ZAD-strategy power converter, EUROMECH Nonlinear Dynamics Conference., Saint Petersburg, RUSSIA, July 2008. [ Links ]
[19] Angulo, F., Olivar, G. and Taborda, J., Continuation of periodic orbits in a zad-strategy con- trolled buck converter, Chaos. Solitons and Fractals, 38, pp. 348-363, 2008. DOI: 10.1016/j.chaos.2007.04.023 [ Links ]
[20] Angulo, F., Análisis de la dinámica de convertidores electrónicos de potencia usando PWM basado en promediado cero de la dinámica del error (ZAD), PhD. Tesis, Universidad Politécnica de Cataluña, Cataluña, España, 2004. [ Links ]
[21] Taborda, J., Análisis de bifurcaciones en sistemas de segundo orden usando PWM y promediado cero de la dinámica del error, MSc. Tesis, Universidad Nacional de Colombia - Sede Manizales, Colombia, Mayo 2006. [ Links ]
[22] Hoyos, F.E., Toro, N. and Angulo, F., Rapid control prototyping of a permanent magnet DC motor using non-linear sliding control ZAD and FPIC, 3rd IEEE Latin American Symposium on Circuits and Systems (LASCAS 2012), Playa del Carmen, Mexico, de Febrero 29 a Marzo 2 de 2012. [ Links ]
[23] Hoyos, F.E., Rincón, A., Taborda, J.A., Toro, N. and Angulo, F., Adaptive quasi-sliding mode control for permanent magnet DC motor, Mathematical Problems in Engineering, Article ID 693685, 12 P, 2013. DOI: 10.1155/2013/693685. [ Links ]
[24] F.E. Hoyos, D. Burbano, F. Angulo, G. Olivar, J. Taborda, and N. Toro, Effects of quantization, delay and internal resistances in digitally ZAD-controlled buck converter. International Journal of Bifurcation and Chaos. 22 (10), 9 P, 2012. DOI: 10.1142/S0218127412502458. [ Links ]
N. Toro-García, received the BSc. degree in Electrical Engineering and the PhD. degree in Automatics from Universidad Nacional de Colombia, Manizales, in 1983 and 2012 respectively; the MSc. degree in Production Automatic Systems from Universidad Tecnológica de Pereira, Colombia, in 2000. He is currently an associate professor in the Department of Electrical Engineering, Electronics and Computer Science, at the Universidad Nacional de Colombia, sede de Manizales. His research interests include nonlinear dynamics of nonsmooth systems, and applications for switched inverters.
Y.A. Garces-Gomez, was born in Manzanares-Caldas, Colombia, in 1983. He received the BSc. Engineering degree in 2009 from the Universidad Nacional de Colombia, Manizales, in Electronic Engineering. Between 2009 and 2011 had a "Colciencias" scholarship for postgraduate studies in engineering - industrial automation at the Universidad Nacional de Colombia. He is currently working for a PhD degree in Engineering at the Universidad Nacional de Colombia. His research interests include power definitions under nonsinusoidal conditions, power quality analysis, and power electronic applications.
F.E. Hoyos-Velasco, received the BSc. degree in Electrical Engineering, the MSc. degree in automatics, and the PhD. degree in automatics from the Universidad Nacional de Colombia, Manizales, Colombia, in 2006, 2009, and 2012, respectively. He is currently professor in the School of Physics, Universidad Nacional de Colombia Sede Medellín. His research interests include nonlinear control, nonlinear dynamics of nonsmooth systems, and applications to dc-dc converters. He is a member of the Scientific and Industrial Instrumentation Research Group, at the Universidad Nacional de Colombia.