Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.192 Medellín July/Aug. 2015
https://doi.org/10.15446/dyna.v82n192.48611
DOI: http://dx.doi.org/10.15446/dyna.v82n192.48611
Design and construction of a reduced scale model to measure lightning induced voltages over inclined terrain
Diseño y construcción de un modelo a escala reducida para medición de tensiones inducidas en un terreno inclinado
Edison Soto-Ríos a, Ernesto Pérez-González b & Javier Herrera-Murcia c
a Facultad de Ingeniería y Arquitectura, Universidad Nacional de Colombia, Manizales, Colombia. easotor@unal.edu.co
b Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia. eperezg@unal.edu.co
c Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia. jherreram@unal.edu.co
Received: October 7th, 2014. Received in revised form: February 11th, 2015. Accepted: July 17th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
In this paper the design and construction of a reduced scale model indented to be used for measuring lightning induced voltages on overhead lines placed over inclined terrain is presented. The paper includes details about the voltage impulse source developed and used in obtaining fast front current surges along the reduced scale lightning channel. The experiment, although, it is only a first approximation of the phenomenon, is useful to validate exact expressions and simulation results obtained from several numerical methods. Additionally, several simulations are made by means of the FDTD method, which have the aim of showing the expected measurements of the reduced scale model.
Keywords: induced voltage, reduce scale model, electromagnetic, lightning, non-flat terrain, overhead lines, distribution lines.
Resumen
En este artículo se presenta el diseño y la construcción de un modelo a escala para medir tensiones inducidas en líneas aéreas ubicadas sobre terrenos inclinados. En este artículo se muestra los detalles de desarrollo de la fuente de tensión creada para producir impulsos rápidos que representen un rayo. El experimento, aunque, es una primera aproximación del fenómeno es útil para validar métodos numéricos que son más flexibles para desarrollar configuraciones más complejas. Adicionalmente se presentan las simulaciones hechas por medio de la metodología de Diferencias finitas para mostrar los resultados esperados por el modelo a escala.
Palabras clave: tensiones inducidas, modelo a escala, electromagnetismo, rayo, descargas eléctricas atmosféricas, terreno no plano, líneas aéreas, líneas de distribución.
1. Introduction
The lightning electromagnetic field causes and important effect on exposed transmission and distribution lines, phone lines and other electrical systems that are close by [1-3]. There is an important influence of the electromagnetic field in the amplitude and wave shape of the lightning induced voltages. In general, lightning electromagnetic fields have usually been calculated when considering only flat terrains [1,3-5]. Nevertheless, many of these lines are placed on mountainous regions such as the Andean and the Alps regions, which are surrounded by mountains and where the flat terrain approximation is not reasonable.
For this reason, it is important to calculate and to measure lightning electric fields and induced voltages over non-flat terrains.
Lightning electromagnetic pulse (LEMP) has been studied worldwide and many theoretical studies have been undertaken. One of the most classical approaches has been made using analytical expressions based on dipole technique [6-8], considering lightning as a straight vertical antenna over a perfectly conducting ground plane. In order to include the ground conductivity it is possible to use the so-called Sommerfeld integrals [9,10]. However do to its complexity, some other approaches have been made such as Cooray-Rubinstein [11-13] who derived a formula for calculating the horizontal electric field over non-perfect soil. Nevertheless, these approaches, in general use a flat terrain.
Several numerical approaches have been used to solve Maxwell equations and include more complex configurations with non-homogeneous propagation media. For example, for LEMP calculations Finite Element Method (FEM) [14,15], method of moments [2,16], and the Finite Difference have been used. The Time Domain method (FDTD) [17-21] will be used in this paper.
The FDTD for solving Maxwell equations, was introduced by Yee [22,23] and has become popular for calculating electromagnetic fields [24]. Several applications from this method have been presented to calculate lightning electromagnetic fields [17-20], in general, all considering flat terrain.
In the case of lighting induced voltages calculation, both analytical equations in Uman et al. [8] or solutions based on numerical methods [1-4,25] have been considered the existence of flat terrain.
Although numerical or analytical approximations can be useful in many cases, a few models have been developed to calculate electromagnetic fields and lightning induced voltages over non-flat terrains. [26,27]. For this reason, some measurements need to be done in order to obtain real behavior of the phenomena. In this paper, we measure those fields and induced voltages by means of a reduced scale model, based on the experience of construction of scale models by authors like Yokoyama [28], Paolone [29], Piantini [30] and Boaventura [31]. Although those experiments were made considering flat terrain, they were adapted to the measurement of lightning electric fields above a flat and non-flat terrain configuration, over a perfect soil. The performance of the reduced scale model is simulated by means of the FDTD-3D method linked with the Agrawal et al. coupling model [32].
The knowledge generated in this work, allows for the improvement of overhead line indirect lightning performance and lightning location systems, which are both related to the improvement of power quality.
2. Reduced Scale Model
A reduced scale model is important for a) the validation of numerical codes that calculate induced voltages produced by lightning electromagnetic pulse (LEMP) and b) the prediction of the Lightning-induced voltages for those cases which, due to their extreme complexity, cannot be simulated with the existing version of these codes [30]. The scale factors can be derived by applying Maxwell's equations to the real system and the reduced-scale model and, and then, by relating the quantities of interest in both systems [30]. The scale factors obtained when the medium is air are shown in Table 1, where p is the ratio between the quantities in the model and in the full-scale system and a is the relation between electric and magnetic fields in the model and in the full scale system.
The choice of length scale factor depends on the available space and the minimal wave front that can be generated and measured [30,31]. The scale factor achieved for this case was p=a=1:200. The reduced scale model was composed by the following components [30,31].
2.1. Ground Plane
The ground plane consisted in a rectangular plane 3x10  was composed of interconnected aluminum plates (corresponding to 600x2000
was composed of interconnected aluminum plates (corresponding to 600x2000  in the full-scale system). Due to scale factor of conductivity shown in Table 1, the aluminum plates can be considered as perfect electric conductors in the full-scale model. The aluminum plates were placed over an iron structure 0.8 m in height. The metallic structure was inclined at a suitable angle to verify the influence of the inclined terrain on lightning induced voltages calculation.
in the full-scale system). Due to scale factor of conductivity shown in Table 1, the aluminum plates can be considered as perfect electric conductors in the full-scale model. The aluminum plates were placed over an iron structure 0.8 m in height. The metallic structure was inclined at a suitable angle to verify the influence of the inclined terrain on lightning induced voltages calculation.
2.2. Return Stroke Channel
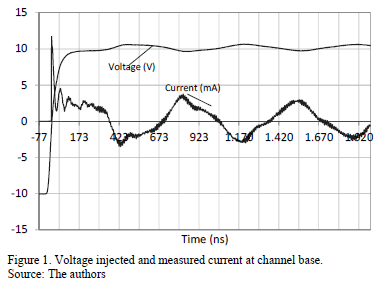
The return stroke channel consists of a cooper coil with a 1.5 cm diameter with a PVC core to give mechanical strength. The copper conductor has a 0.5mm radius. The height of the total rod is 6 m, although due to local restrictions, it was limited to 5m. The injection of a step voltage at rod base has a current response as Fig. 1 shows.
According to Fig. 1, the travel time of the wave from the bottom of the channel and back again is approximately 400 ns. The return stroke velocity is equal to:
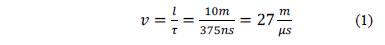
The velocity measured along the channel is approximately 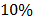 of that of the speed of light in free space. The surge impedance can be obtained dividing the voltage and the current measured in the first 400 ns.
of that of the speed of light in free space. The surge impedance can be obtained dividing the voltage and the current measured in the first 400 ns.
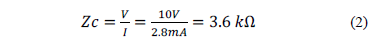
2.3. Impulse Current Generator
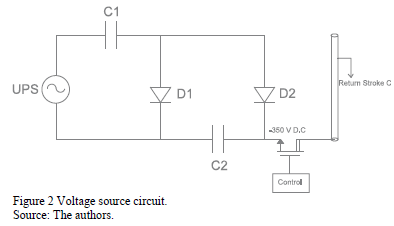
The current is generated when a voltage source is injected into the base of the lightning channel. The voltage source circuit is shown in Fig. 2. It is composed by an alternating voltage source through an uninterruptible power supply (UPS), and a voltage multiplier circuit of 2 steps that generates a total voltage of -350 V D.C. (The negative polarity value does not affect the measurements made of lightning induced voltages). The stored voltage in capacitors is discharged to the lightning channel by means of a very fast switching electronic device (MOSFET STD2NK100Z). A control circuit of the MOSFET is composed by an oscillator 555 that generates a pulsed voltage with a frequency of 1 Hz and a width pulse of 4ms (enough time for the expected duration of measurements -approximately 200ns). The discharge is repetitive and has the aim of reducing noise in measurements. The constructed voltage source is shown in Fig. 3.
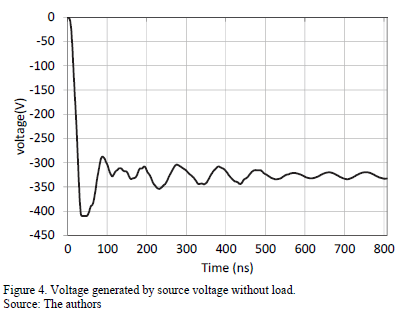
The voltage generated by the source without load is shown in Fig. 4. It is possible to see an approximately front time of 40 ns, equivalent to 8 us in a full-scale system.
2.4. Overhead distribution line
The line is a copper conductor, 5m long, 5 cm high and with a radius of 0.46 mm. The line at full-scale will be equivalent to a 1km line, 10 m height and 80 mm radius.
2.5. Measuring System
The electric field is measured by means of a ring, concentric with the return stroke channel. The measured voltage at this ring is proportional to electric field [30]. The induced voltage is measured at the beginning and at the end of the line by means of an oscilloscope Tektronix with a bandwidth of 100 MHz, 1GS/s and 1 mV/div.
3. Methodology for calculating lightning electromagnetic fields and lightning induced voltages
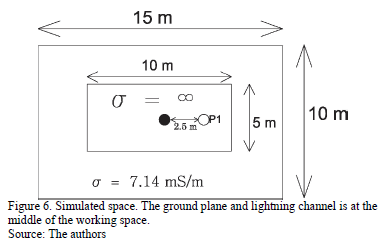
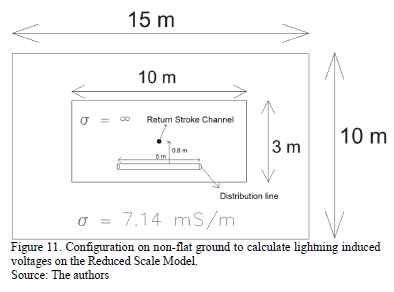
In order to simulate the reduced scale model, the finite difference time domain method (FDTD) was employed in the 3-D Cartesian coordinates system [23]. It was simulated by using a metallic plate 3 x 10 m2 with a very high conductivity (s=1e8), which was surrounded by a concrete space (corresponding to the soccer field where the model was placed, see Fig. 5). The concrete conductivity was assumed to be s=7.14 mS/m.
The grid dimensions were 15 (in x) ' 10 (in y) ' 6 (in z) m3 (see Fig. 6) and the space step was set as 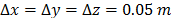 , due to the available computational capability. The inclined terrains were represented by staircases in 3D [23].
, due to the available computational capability. The inclined terrains were represented by staircases in 3D [23].
A lightning channel was simulated with a base current, characterized by a peak value of 170 mA and a front time of 20 ns, corresponding approximately to the initial estimated values of the channel base current obtained from the reduced scale model measurements. It can be represented by a Heidler function [19], with the following parameters: 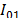 =160 mA,
=160 mA, 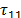 = 4.47 ns,
= 4.47 ns,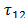 =200 ns. The lightning channel was placed at the middle of the working space. For simplicity, a TL model was used to represent the return stroke current along the channel [8,33]. The height of the constructed channel (5 m) was simulated, and the return stroke velocity was measured (30 m/
=200 ns. The lightning channel was placed at the middle of the working space. For simplicity, a TL model was used to represent the return stroke current along the channel [8,33]. The height of the constructed channel (5 m) was simulated, and the return stroke velocity was measured (30 m/ s) at this channel (See Section 0).
s) at this channel (See Section 0).
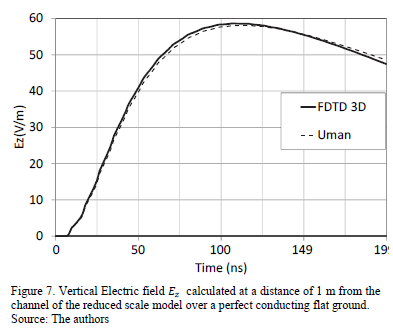
The electromagnetic field obtained by FDTD code [22] was validated by comparing the electric field calculated by the 3D-FDTD methodology with the analytical expressions derived by Uman [8] for LEMP calculation. The vertical electric field is calculated at a distance of 1 m from the lightning channel at ground level over perfectly conducting flat terrain, as shown in Fig. 7. It is possible to see good agreement between the two methods.
The Agrawal et al. coupling model [32] will be used throughout this paper in order to calculate the lightning induced voltages on overhead lines. This model is implemented in the YalukDraw software [34,35], that was developed by the first two authors. It is software that allows the lightning performance of overhead distribution networks to be calculated, and it is based in a previous piece of software called Yaluk, linked with ATP by means of foreign MODELS. This was done thanks to the collaboration of the Power Systems research group from the University of Bologna. For non-flat terrain, the Yaluk Draw has been modified to be used as input for the electric fields, calculated by means of the 3D-FDTD method. Due to the fact that the TEM approximation is used (derived of the transmission line theory), the electric and magnetic fields can be related and it is not necessary get the magnetic field into the program.
In order to fulfill the conditions of the coupling model for evaluating the lightning induced voltages, it is necessary to make some considerations regarding the horizontal and vertical electric fields calculated on the FDTD grid. In all cases, the electric field parallel to the line El, and the average vertical electric field Ev perpendicular to the terrain were obtained [36] at the beginning and at the end of line end, as shown in the Fig. 4. Although, for flat terrain the vertical electric field is approximately constant below the line, the vertical electric field in the soil can be considered as an input parameter for the coupling model. For non-flat terrain there is a great variability on the fields below the line, and for this reason it is preferable to calculate the average vertical electric field.
4. Simulated Electric fields on the reduced scale model
Two configurations are simulated according to the arrangements to be implemented in the reduced scale model, as shown below:
4.1. Flat ground
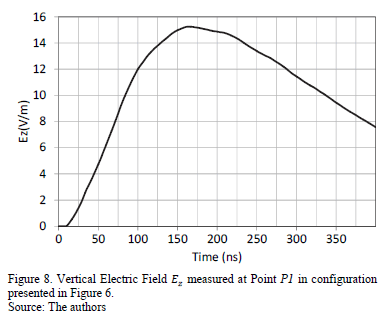
The first is the configuration described in Fig. 6, where a ground plane is placed in the middle of a working volume with a soil of concrete. The vertical electric field  , measured at point P1 is seen in Fig. 8.
, measured at point P1 is seen in Fig. 8.
4.2. Inclined terrain
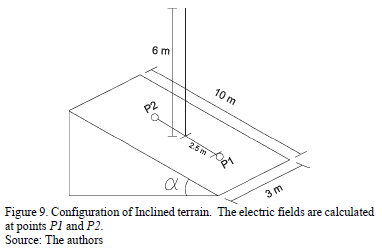
The second configuration is the result of inclining the ground plane of the previous configuration, at an angle a of 30° as shown in Fig. 9. With the aim of being able to make a comparison, The normal component of the electric field Ep was calculated in each simulation (for flat terrain the perpendicular electric field  is equal to vertical electric field
is equal to vertical electric field  ).
).
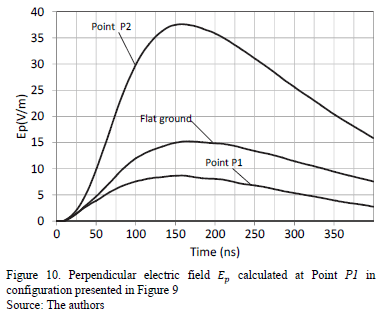
In Fig. 10 the perpendicular electric field  , obtained at points P1 and P2 compared with the vertical electric field for flat terrain is presented. The electric field at Point P2 is enhanced in magnitude compared with the case of flat terrain. This is explained by the closeness between the lightning channel and measurement point P2. The perpendicular electric field
, obtained at points P1 and P2 compared with the vertical electric field for flat terrain is presented. The electric field at Point P2 is enhanced in magnitude compared with the case of flat terrain. This is explained by the closeness between the lightning channel and measurement point P2. The perpendicular electric field  at point P1 is decreased in magnitude compared with the case of flat terrain. This can be explained due to that fact that the lightning channel is farther from the measurement point P1. The tendency of the results presented previously in Fig. 10, match the inclined lightning channel studies previously published [16,37] It is explained because according to the method of images, an inclined lightning channel is equivalent to vertical lightning that strikes inclined terrain [25].
at point P1 is decreased in magnitude compared with the case of flat terrain. This can be explained due to that fact that the lightning channel is farther from the measurement point P1. The tendency of the results presented previously in Fig. 10, match the inclined lightning channel studies previously published [16,37] It is explained because according to the method of images, an inclined lightning channel is equivalent to vertical lightning that strikes inclined terrain [25].
The trend presented above is applicable to points located aside lightning channels (according to other simulations not here presented). It implies that a line placed over inclined terrain has a vertical electric profile highly variable from that obtained for flat terrain (due symmetry of the fields). For this reason, a different magnitude and wave-shape of lightning induced voltages are expected.
5. Simulated induced Voltages on the reduced scale model
In order to obtain the expected measurements of induced voltages on the reduced scale model, the previous configurations were slightly modified with the aim to adapt the results found in the reduced scale model constructed. In this case the simulated peak current was 88 mA with a front time of 40 ns. The current was represented by a Heidler function [19] with the following parameters: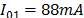 ,
, 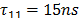
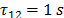
5.1. Flat ground
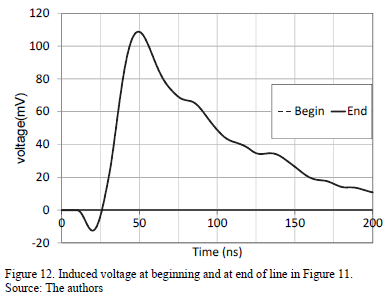
The distribution line simulated in flat terrain is shown in Fig. 11. It is 5m long, 5cm high and is located 0.8 m from the return stroke channel, as described in Section 0. The induced voltages calculated at both extremities of the line are shown in Fig. 12. Some reflections and a double polarity are seen as the result of the presence of the concrete terrain that surrounds the experimental setup.
5.2. Inclined terrain
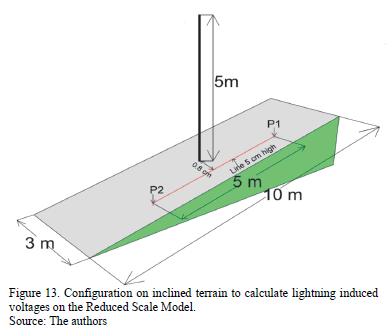
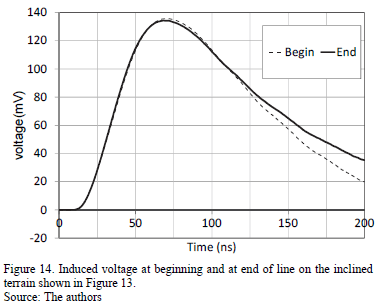
The configuration of inclined terrain to be simulated is shown in Fig. 13. Essentially, it is the result of rotating the system shown in Fig. 11 at an angle of 30°. The distribution line is 5m long, placed parallel to the terrain. The induced voltage calculated at both extremities of the line is shown in Fig. 14. It is possible to see a slight increment of the induced voltage compared with the flat terrain case. Following the tendency of the electric field, the induced voltage is increased at point P2 (end of line), while it is decreased at Point P1 (beginning of line).
6. Conclusions
The design of a reduced scale model to measure the electric field over an inclined terrain has been presented. The results of this experiment serve as validation of numerical codes previously developed to determine the influence of the orography on lightning electromagnetic fields. This knowledge is useful for the improvement of lightning location systems and lightning induced voltages calculation.
A modeling of the reduced scale model has been presented. The model was composed by a highly conductive ground plane inclined a degrees with respect to a flat ground surface. The lightning channel was modeled by means of a vertical antenna excited by a voltage impulse source developed from an electronic voltage multiplier system. Measurements of the normal component of the electric field and of induced voltages on an overhead line were taken from the experimental setup and then compared to simulation results obtained from a FDTD representation of the measurement scenario.
The electric field above an inclined terrain results show a significant difference with respect to the case of flat terrain. The electric field calculated at point P1 decreases its value with respect the flat terrain case, because the farness of the point to the lightning channel, while at point P2 the electric field increase its magnitude as a result of the closeness with the lightning channel.
The induced voltages calculated on the reduced scale model show a little increase when compared to the flat terrain case and the same tendency of the electric fields.
It is expected that the results obtained by using the Finite Difference time domain method in 3-D Cartesian coordinates system could be validated by the constructed reduced scale model, so as the reliable and real data could be used to improve the performance of distribution networks placed over non-flat terrain.
Acknowledgments
he authors would like to thank to the Colombian Administrative Department of Science and Technology - COLCIENCIAS for their support of this research, and the Universidad de Antioquia for their support with the measurement devices used in this experiment.
References
[1] Nucci, C.A., Rachidi, F. and Ianoz, M.V., Lightning induced voltages on overhead lines, IEEE Trans Electromagn Compat, 35 (1), pp. 75-86, 1993. DOI: 10.1109/15.249398 [ Links ]
[2] Baba, Y. and Rakov, V.A., Voltages induced on an overhead wire by lightning strikes to a nearby tall grounded object, IEEE Trans Electromagn Compat, 48 (1), pp. 212-224, 2006. DOI: 10.1109/TEMC.2006.870807 [ Links ]
[3] Cooray, V. and Scuka, V., Lightning-Induced overvoltages in power lines: Validity of various approximations made in overvoltage calculations, IEEE Trans Electromagn Compat, 40, pp. 355-363, 1998. DOI: 10.1109/15.736222 [ Links ]
[4] Borghetti, A., Nucci, C.A. and Paolone, M., An improved procedure for the assessment of overhead line indirect lightning performance and its comparison with the IEEE Std. 1410 Method, IEEE Trans. Power Deliv., 22 (1), pp. 684-692, 2007. DOI: 10.1109/TPWRD.2006.881463 [ Links ]
[5] Yutthagowith, P., Ametani, A., Nagaoka, N. and Yoshihiro, B., Lightning-Induced voltage over lossy ground by a hybrid electromagnetic circuit model method with Cooray - Rubinstein formula, 51, pp. 975-985, 2009. [ Links ]
[6] Master, M.J. and Uman, M.A., Transient electric and magnetic fields associated with establishing a finite electrostatic dipole, Am. J. Phys., 51 pp. 118-126, 1983. DOI: 10.1119/1.13310 [ Links ]
[7] Rubinstein, M., Methods for calculating electromagnetic fields from a known source distribution: Application to lightning, IEEE Trans. Electromagn. Compat., 31 (2), pp. 183-189, 1989. DOI: 10.1109/15.18788 [ Links ]
[8] Uman, M.A. and Krider, E.P., The electromagnetic radiation from a finite antenna, Am. J. Phys., 43, pp. 33-38, 1975. DOI: 10.1119/1.10027 [ Links ]
[9] Sommerfeld, A., Uber die ausbreitung der wellen in der drahtlosen telegraphie, Ann. Phys., 4 (28), pp. 665-736, 1909. DOI: 10.1002/andp.19093330402 [ Links ]
[10] Delfino, F., Procopio, R. and Rossi, M., Lightning return stroke current radiation in presence of a conducting ground: 1. Theory and numerical evaluation of the electromagnetic fields, J. Geophys. Res. Atmospheres, 113 (D5), pp. 1-10, 2008. DOI: 10.1029/2007JD008553. [ Links ]
[11] Cooray, V., Horizontal field generated by return strokes, Radio Sci., 27 (5), pp. 529-537, 1992. DOI: 10.1029/91RS02918 [ Links ]
[12] Rubinstein, M., An approximate formula for the calculation of the horizontal electric field from lightning at close, intermediate, and long range, IEEE Trans. Electromagn. Compat., 38 (3), pp. 531-535, 1996. DOI: 10.1109/15.536087 [ Links ]
[13] Cooray, V., Some considerations on the 'Cooray-Rubinstein' approximation used in deriving the horizontal electric field over finitely conducting ground, IEEE Trans. Electromagn. Compat., 44 (4), pp. 560-566, 2002. DOI: 10.1109/TEMC.2002.804774 [ Links ]
[14] Jin, D.J.R.J.M., Finite element analysis of antenna and arrays , 2009. John Wiley & Sons In, Hoboken, 2009. [ Links ]
[15] Napolitano, F., Borghetti, A., Nucci, C., Rachidi, F. and Paolone, M., Use of the full-wave finite element method for the numerical electromagnetic analysis of LEMP and its coupling to overhead lines, Proc. of the 7th Asia-Pacific International Conference on Lightning, Nov. 1-4, 2011, Chengdu, China. DOI: 10.1109/apl.2011.6110132 DOI: 10.1016/j.epsr.2012.05.002 [ Links ]
[16] Moini, R., Sadeghi, S.H.H., Kordi, B. and Rachidi, F., An antenna-theory approach for modeling inclined lightning return stroke channels, Electr. Power Syst. Res., 76 (1), pp. 945-952, 2006. DOI: 10.1016/j.epsr.2005.10.016 [ Links ]
[17] Cardoso, J.R. and Sartori, C.A.F., An analytical-FDTD method for near LEMP calculation, IEEE Trans. Magn., 36 (4), pp. 1631-1634, 2000. DOI: 10.1109/20.877754 [ Links ]
[18] Yang, C. and Zhou, B., Calculation methods of electromagnetic fields very close to lightning, IEEE Trans. Electromagn. Compat., 46 (1), pp. 133-141, 2004. DOI: 10.1109/TEMC.2004.823626 [ Links ]
[19] Heidler, F., Cvetic, J. and Stanic, B.V., Calculation of lightning current parameters, IEEE Trans. Electromagn. Compat., 14 (2), pp. 399-404, 1999. DOI: 10.1109/61.754080 [ Links ]
[20] Mimouni, A., Rachidi, F. and Azzouz, Z., Electromagnetic environment in the inmediate vicinity of a lightning return stroke, J. Light. Res., 2, pp. 64-75, 2007. [ Links ]
[21] Baba, Y. and Rakov, V.A., Influence of strike object grounding on close lightning electric fields, J. Geophys. Res., 113 (D12), pp. n/a. 2008. DOI: 10.1029/2008JD009811. [ Links ]
[22] Yee, K.S., Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media, IEEE Trans. Antennas Propag., Ap-14, pp. 302-307, 1966. [ Links ]
[23] Taflove, A. and Hagness, S.C., Computational Electrodynamics: the finite-difference time-domain method, 3rd edition. Artech House, 2005. [ Links ]
[24] Wilson, On some determinations of the sign and magnitude of electric discharges in lightning flashes, Proc Roy Soc, pp. 555-574, 1916. [ Links ]
[25] De Conti, A., Perez, E., Soto, E., Silveira, F.H., Visacro, S. and Torres, H., Calculation of lightning-induced voltages on overhead distribution lines including insulation breakdown, IEEE Trans. Power Deliv., 25 (4), pp. 3078-3084, 2010. DOI: 10.1109/TPWRD.2010.2059050 [ Links ]
[26] Soto, E., Perez, E. and Herrera, J., Electromagnetic field due to lightning striking on top of a cone-shaped mountain using the FDTD, IEEE Trans. Electromagn. Compat., 56 (5), pp. 1112-1120, 2014. DOI: 10.1109/TEMC.2014.2301138 [ Links ]
[27] Soto, E., Perez, E. and Younes, C., Influence of non-flat terrain on lightning induced voltages on distribution networks, Electr. Power Syst. Res., 113, pp. 115-120, 2014. DOI: 10.1016/j.epsr.2014.02.034 [ Links ]
[28] Yokoyama, S., Calculation of lightning induced voltages on overhead multiconductor lines, IEEE Trans. Power Appar. Syst., 103 (1), pp. 100-108, 1984. DOI: 10.1109/TPAS.1984.318583 [ Links ]
[29] Paolone, M., Nucci, C.A. and Petrache, E., Mitigation of lightning-induced overvoltages in medium voltage distribution lines by means of periodical grounding of shielding wires and of surge arresters: Modeling and experimental validation, 19 (1), pp. 423-431, 2004. [ Links ]
[30] Piantini, A., Member, S., Janiszewski, J.M., Borghetti, A., Nucci, C.A. and Paolone, M., A scale model for the study of the LEMP response of complex power distribution networks, IEEE Trans Power Deliv., 22 (1), pp. 710-720, 2007. DOI: 10.1109/TPWRD.2006.881410 [ Links ]
[31] Boaventura, W. do C., Estudo da tensão induzida ém lihnas aéreas por descargas atmosféricas utilizando técnicas de modelo reduzido, 1990. [ Links ]
[32] Agrawal, A., Price, H. and Gurbaxani, S., Transient response of multiconductor transmission lines excited by a nonuniform electromagnetic field, IEEE Trans. Electromagn. Compat., 22 (2), pp. 119-129, 1980. DOI: 10.1109/TEMC.1980.303824 [ Links ]
[33] Uman, M.A. and Mclain, D., Calculations of lightning return stroke models, J. Geophys. Res., 85, pp. 1571 -1583, 1985. [ Links ]
[34] Perez, E. y Torres, H., Modelado y experimentación de tensiones Arquitectura, Universidad Nacional de Colombia, 2010. [ Links ]
[35] Perez, E. y Soto, E., Yaluk draw: Software especializado para análisis del desempeño de líneas de distribución ante impacto de rayos, Avances en Ingeniería Eléctrica, 4 (1), pp. 1-8, 2013. [ Links ]
[36] Soto, E., Perez, E. and Herrera, J., Electromagnetic field due to lightning striking on top of a cone-shaped mountain using the FDTD, IEEE Trans. Electromagn. Compat., 73, [Online], 2014. [ Links ]
[37] Rameli, N., Kadir, M.Z.A.A., Izadi, M., Gomes, C. and Jasni, J., On the influence of inclined lightning channel on lightning induced voltage evaluation evaluation of coupling, in: International Conference on Lightning Protection (ICLP), Vienna, Austria, 2012. DOI: 10.1109/ICLP.2012.6344250 [ Links ]
E. Soto-Ríos, was born in Manizales, Colombia, South America on April 29th, 1986. He received his BSc. in 2008 and MSc. in 2011 in Electrical Engineering, both from the Universidad Nacional de Colombia. At present he is a PhD. Electrical Engineering Student at the Universidad Nacional de Colombia, Manizales, Colombia. His areas of interest are electromagnetic compatibility, lightning protection and lightning induced voltages.
E. Perez-González, was born in Bogota, Colombia, South America on November 21st, 1976. He received his BSc. in 1999, MSc. in 2002 and PhD. in 2006 all of them from the Universidad Nacional de Colombia in Electrical Engineering and High Voltage Studies. He worked for one year with the Power System research group at the University of Bologna - Italy, working on lightning induced voltage. He has been working with the research group PAAS-UN in Colombia since 1998. He is has been an associate professor since 2006 in the Universidad Nacional de Colombia, Medellin, Colombia. His special fields of interest include lightning phenomena analysis and power system protection.
J. Herrera-Murcia, was born in Bogota, Colombia, on July 28, 1976. He received his BSc. in 1999, MSc. in 2002 and PhD. in 2006, all of them from the Universidad Nacional de Colombia in Electrical Engineering and High Voltage Studies. He has been involved with lightning protection systems and power systems transients with emphasis on lightning-induced voltages. He has been an associate professor since 2006 in the Universidad Nacional de Colombia, Medellin, Colombia.