DOI: http://dx.doi.org/10.15446/dyna.v83n195.45396

A multiobjective approach for non-discretionary variables in data envelopment analysis

Un enfoque multiobjetivo para variables no discrecionales en análisis envolvente de datos

 

Lidia Angulo-Meza ^a, João Carlos Correia Baptista Soares-de Mello ^b & Silvio Figueiredo-Gomes-Júnior ^c

 

^a Departamento de Engenharia de Produção, Universidade Federal Fluminense, Fluminense, Brasil. lidia_a_meza@pq.cnpq.br
^b Departamento de Engenharia de Produção, Universidade Federal Fluminense, Fluminense, Brasil. jcsmello@producao.uff.br
^c Departamento de Engenharia de Produção, Universidade Estadual da Zona Oeste, Rio de Janeiro, Brasil. silviogomes@uezo.rj.gov.br

 

Received: September 3^rd, 2014. Received in revised form: July 29^th, 2015. Accepted: August 18^th, 2015.

 

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

---

Abstract
Data Envelopment Analysis is a non-parametrical approach for efficiency evaluation of so-called DMUs (Decision Making Units) and takes into account multiple inputs and outputs. For each inefficient DMU, a target is provided which is constituted by the inputs or outputs levels that are to be attained for the inefficient DMU to become efficient. However, multiobjective models, known as MORO (Multiobjective Model for Ratio Optimization) provide a set of targets for inefficient DMU, which provides alternatives among which the decision-maker can choose. In this paper, we proposed an extension of the MORO models to take into account non-discretionary variables, i.e., variables that cannot be controlled. We present a numerical example to illustrate the proposed multiobjective model. We also discuss the characteristics of this model, as well as the advantages of offering a set of targets for the inefficient DMUs when there are non-discretionary variables in the data set.

Keywords: Data Envelopment Analysis; Multi-objective model; Non-discretionary variables; non-radial models.

Resumen
El Análisis Envolvente de Datos es un enfoque no paramétrico para la evaluación de la eficiencia de las llamadas DMUs - Unidades Tomadores de Decisión, teniendo en cuenta múltiples entradas y salidas. Para cada DMU ineficiente, se proporciona una meta que está constituida por los niveles de entradas o salidas que deben ser alcanzados para que la DMU ineficiente se vuelva eficiente. Sin embargo, los modelos multiobjetivo, llamados modelos MORO (del ingles Multiobjective model for Ratio Optimization) proporcionan un conjunto de metas para DMU ineficientes, lo que ofrece alternativas de las cuales el decisor puede elegir. En este trabajo se ha propuesto una extensión de los modelos MORO para tener en cuenta las variables no-discrecionales, es decir, variables que no se pueden controlar. Se presenta un ejemplo numérico para ilustrar el modelo multiobjetivo propuesto. También se discuten las características de este modelo, así como las ventajas de ofrecer un conjunto de metas para la DMU ineficientes cuando hay variables no discrecionales en el conjunto de datos.

Palabras clave: Análisis Envolvente de Datos; Modelos Multiobjetivo; Variables no-discrecionales; modelos no-radiales.

---

 

1. Introduction

Data Envelopment Analysis - DEA [1] is a non-parametric approach for efficiency evaluation of units called DMUs (Decision Making Unit) that use the same inputs to produce the same outputs. An efficiency index is provided for every DMU and for inefficient DMUs, a target is also provided among other information. This target gives the input or output levels for an inefficient DMU to become efficient. In contrast to this non parametric technique, there are a number of parametric techniques used for instance by [2] to measure efficiency.

However, there may be problems in reaching the one target provided for the DEA model as it may not be viable from a managerial or operational point of view. Therefore, models have been presented that seek other targets taking into account decision-makers' preferences [3,4]. The MORO models [5,6] were presented as a way of proving a set of targets instead of a single target for each inefficient, giving the decision-maker flexibility to choose the viable target.

On the other hand, in classical DEA models, analyses can be output oriented or input oriented. That is, we assume that all outputs or all inputs can be modified, or controlled. In real cases, this may not be possible. Some variables are non-controllable due to external or internal factors, yet at the same time, the DEA analysis has to be performed dealing with this fact. The variables that cannot be changed at discretion are called non-discretionary variables. Some authors have presented methods that deal with these situations: first, Banker and Morey [7], then Golany and Roll [8], Camanho et al. [9] and Estelle et al. [10], among others. All these models provide one target for each inefficient DMU.

In this paper, we present an extension of the MORO models to determine a set of targets for inefficient DMUs when there are non-discretionary variables in the analysis. We therefore take advantage of the results of the multiobjective model providing the decision-maker with flexibility, and we take into account non-discretionary variables that are part of the evaluation. To help the decision-maker to choose a target, we also provide a non-radial efficiency index for each target.

We applied this model to a simple and didactic numerical example to show the simplicity of the approach.

This paper is organized as follows. In Section 2, we present the models for non-discretionary variables and the multiobjective models for determining a set of targets in DEA, the MORO models. The proposed multiobjective model with non-discretionary variables is presented in Section 3. After that, in Section 4, we present a numerical example. We present some final comments in Section 5.

 

2. DEA non-discretionary and MOLP-DEA models

DEA classical models, CCR [1] and BCC [11] use multiple input and multiple outputs to evaluate DMUs. This is carried out by reducing inputs or increasing outputs equiproportionally, known as radial efficiency.

Nonetheless, the radial efficiency, suitable in many cases, may not be appropriate for many real cases. As a result, models that deal with different situations have been presented. The one situation relevant for this study is the existence of non-discretionary variables. They cannot vary at the discretion of the decision-maker. As part of the analysis they have to be taken into account.

On the other hand, for inefficient DMUs, one target is radially determined. In some cases, the unique target determined for inefficient DMUs may not be feasible due to operational or managerial characteristics. Therefore, models have been developed to present alternative targets [3,4]. The multiobjective DEA model called the MORO model [5,6] was introduced as an alternative to determine a set of targets instead of a single target determined by the DEA mono objective models.

In this section, we present a brief review of non-discretionary DEA models as well as one of the models. We also present the MORO model that will be used in this study.

2.1. Non-Discretionary models in DEA

As mentioned previously, in some real cases, DEA classical models do not take into account variables that cannot be controlled or modified due to fixed production factors or external ones. There are some uncontrollable factors that affect efficiency but do not belong to the production process itself. These variables are commonly called environmental variables and they are not included explicitly in the DEA model. To deal with those variables often requires the use of the so-called multistage DEA model.

In this paper, we are not concerned with those kinds of variables. Rather, we are concerned with the variable that belongs to the production process but cannot be modified according to the decision-maker discretion. In other words, they are fixed for each DMU. For example: when evaluating public schools or public hospitals in Brazil, the number of employees can be one of the inputs. What happens is that by law, they cannot be fired. So, in an input oriented approach, the number of employees variable must be treated as fixed, i.e., a non-discretionary variable as defined in the previous paragraph. We will review papers that deal with the kind of non-discretionary variables as we have defined and we will briefly mention papers dealing with other kinds of non-discretionary or environmental variables. For a more detailed explanation about differences between these two kinds of non-discretionary variables see Camanho et al. [9].

The first model was introduced by Banker and Morey [7] and the input oriented variable returns to scale model is presented in (1).

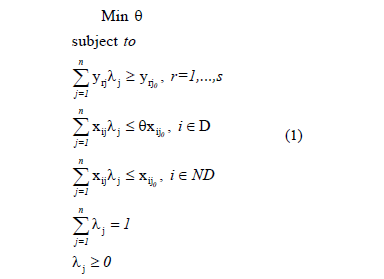
In this model, we can see that inputs are divided into two sets: discretionary (D), that can be controlled, and non-discretionary (ND), or non-controllable. The equiproportional reduction applies only to the discretionary inputs (set D). Therefore, the only difference between this model and the standard variable returns to scale DEA model [11] is the removal of factor q from the right-hand side of the non-discretionary inputs. This model provides an efficiency index and a unique target for each inefficient DMU, and it has been widely used, for instance, in Fonseca et al. [12] and Soares de Mello et al. [13].

Banker and Morey [7] also provided the output oriented variable returns to scale DEA model for non-discretionary variables. Analogous to model (1), in the output oriented version, outputs are divided into two groups and then the factor is only multiplied to the controllable outputs.

The constant returns to scale version of this model can be easily formulated with the exclusion of the convexity constraint [14,15]. Another version of this model was introduced by the same authors, Banker and Morey [7].

Golany and Roll [8] extended Banker and Morey's constant returns to scale model to account for non-discretionary variables in both inputs and outputs. Cooper et al. [14] also presented a model for the same problem, which takes into account the existence of non-controllable variables in both the input and output sets.

Concerning the non-discretionary external factors that affect the production process, also known as environmental variables, (see for instance Fried [16,17]), Daraio and Simar [18,19], Muniz [20], Gomes et al. [21], Lima et al. [22] among others.

2.2. The MORO models

In many cases, the single target provided by the DEA classical models may not be feasible, due to operational or managerial problems, or simply because we have additional information about the variables. Some alternative models have been presented by Thanassoulis and Dyson [3] and Zhu [4]. These models require the decision-maker to establish the importance of each input (output) reduction (increase) factor. For each set of value judgments, a single target is determined.

On the other hand, the MORO models [5,6] provide a non-singular set of targets for each DMU and the decision-maker's information is required a posteriori. So, it is not necessary to run the model with every change in the decision-maker's value judgments. Moreover, as we will see in section 3, adapting the MORO models to account for non-discretionary variables requires only a modification in one subset of restrictions.

The most common MORO model is the MORO-D-CRS, presented in (2).

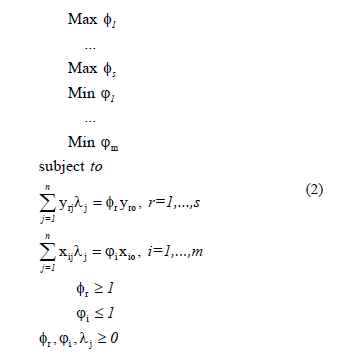
This model is very similar to the envelopment version of the CCR model. This model allows each variable to change independently, and not in a radial way as the classical DEA models. The f_r factor is the variation for the output r, j_i factor is the variation for the input i. We have one objective function for each factor, and we try to maximize the factor for the outputs and minimize the factors for the inputs. The restrictions ensure that we will find projections in the efficient frontier, since the variations of inputs and outputs are independent we replace the inequalities by equalities [5,6]. The last two restrictions guarantee that the outputs will maintain their levels or increase and the inputs will maintain their levels or decrease. In this way we will obtain targets that dominate the DMU o under evaluation, in an approach similar to the Thanassoulis and Dyson mono-objective model [3]. Therefore this model is called MORO with dominance, constant returns to scale, or MORO-D-CRS.

In an approach similar to the Zhu mono-objective model [4], the last two restrictions could be removed. In doing that, any point in the efficient frontier can be a feasible target for the inefficient DMU,. This model is called MORO CRS without dominance, or MORO-CRS.

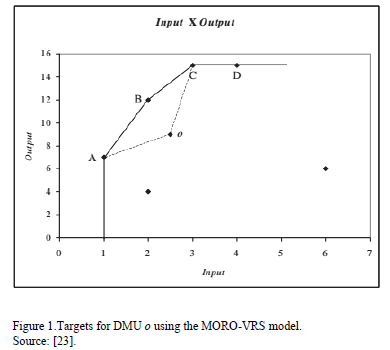
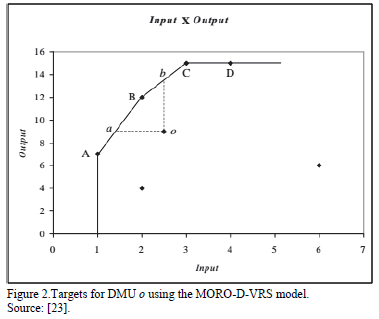
To illustrate these situations, we present Figs. 1 and 2 from Soares de Mello et al. [23]. In both figures a variable returns to scale frontier is shown. In Fig. 1, possible targets for DMU o using the MORO-VRS model are shows. In Fig. 2, the MORO-D-VRS is used to determine the targets for DMU o. To obtain the variable returns to scale we introduce the convexity restriction (3) in the model. Such a model would be called MORO-VRS or MORO-D-VRS depending whether we consider dominance or not, as in the aforementioned Figures.

We have to point out that it is not only the extreme points that are targets for the inefficient DMU, but also the linear combinations of these points that lie in the efficient frontier can be possible targets. This will happene depending on the method used for solving the multiobjective problem. For example, in Fig. 2, for DMU o, the extreme points or targets, are a, B and b. Also, any point in segments aB and Bb are possible targets for DMU o. Therefore, in theory, we will have an infinite set of targets depending on the method used for solving the multiobjective problem [23].

According to Clímaco et al. [24], the MORO models can be classified into the group that uses multiobjective models to solve problems in DEA. Also, according to the same authors the MORO models may be seen as a formalization of the Golany [25] algorithm.

An efficient DMU is on the Pareto efficient frontier and thus 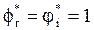, " r, i, as the equality restrictions of the model require nil value slacks. If this is not the case, the targets for the outputs are given by (4) and the targets for the inputs are given by (5).

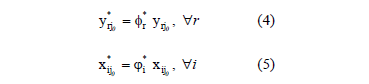
Therefore, the final value 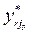and 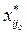depends on the target chosen by the decision-maker and thus we define the values for 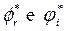among the solutions of the MORO model chosen. In this way, alternative targets can be obtained based on the preferences of the decision-maker.

 

3. MORO model with non-discretionary variables

As seen previously, the MORO models determine a set of targets for each inefficient DMU. We assume that all variables may change their levels in order to be efficient. In some cases, one of the set's targets may change the level of one variable at a time. Unfortunately, there is no guarantee that the set of targets will always contain a target for any specific non-discretionary variable. Also, the MORO models allow different degrees of change in input and output levels. Thus, to account for non-discretionary variables, we present an extension of the MORO models. The resulting model is in (6) and is called MORO-D-ND, the MORO model with dominance and inequality restrictions with non-discretionary variables, or simply MORO-ND.

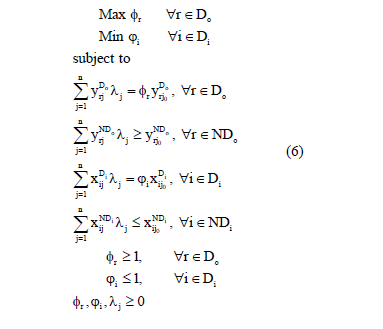
In this model, we have a factor for every discretionary input (D_i) and output (D_o), so the number of objective functions is the number of discretionary variables. We have divided the restrictions of the inputs and outputs in two groups, one that deals with discretionary variables (D_o for outputs and D_i for inputs) and one that deal with non-discretionary variables (ND_o for outputs and D_i for inputs). For the first group, as the variables are allowed to change independently, we have a set of equalities, in a similar approach as the MORO models (2). For the second one, in which variables cannot be changed, we set inequalities similar to the envelopment model, in an approach similar to the Banker and Morey's model presented in (2). The last two restrictions of this model are the dominance restrictions, so for the output, we can increase or maintain the level and for the input we can reduce or maintain the level.

As for the other MORO models, we can obtain a set of targets taking into account the variables that are fixed, for any reason, in the analysis. Obviously, the added advantage is that we do not have to specify an orientation (input or output) for the model, because it is a non-radial model.

We can also account for the variable returns to scale introducing the convexity restriction (7).

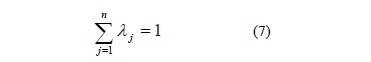
Also, we can find targets without dominance by eliminating the two last restrictions in model (6).

We can also identify an efficient DMU when 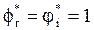, " r, i, as the equality restrictions of the model require nil value slacks. If this is not the case, the targets for the variables are given by equations (8) and (9).

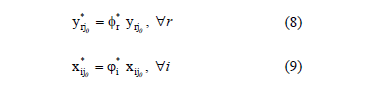
In this case, the non-discretionary variables will maintain their levels. Once again, the alternative targets can be obtained based on the preferences of the decision-maker.

 

4. Numerical example

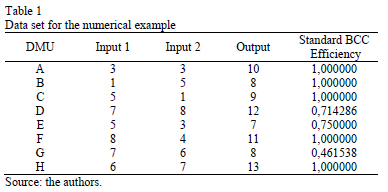
In this section, we present an illustrative example with 2 inputs and 1 output. Table 1 presents the data set for the numerical example and the standard BCC efficiency index calculated by the SIAD software [26].

Using the BCC model, DMUs A, B, C, F and H are efficient. Now we turn our attention to the targets for inefficient DMUs. To obtain a set of targets for each inefficient DMU, instead of only one target, we use the MORO-D-ND model in (6) with restriction (7).

For DMU D the model is formulated as in model (10).

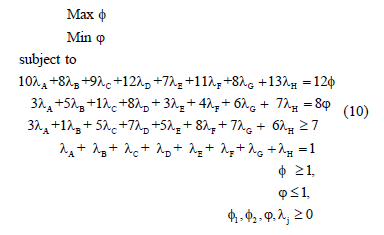
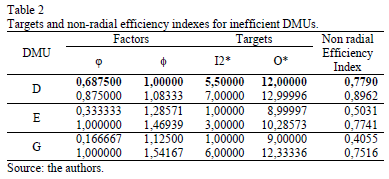
In Table 2 we show set of targets for all inefficient DMUs, Input 1 being the non-discretionary variable. We use TRIMAP [27, 28] to solve the multiobjective model, so we have obtained only basic solutions. We also show an efficiency index using the model developed by Gomes Junior et al. [29] .

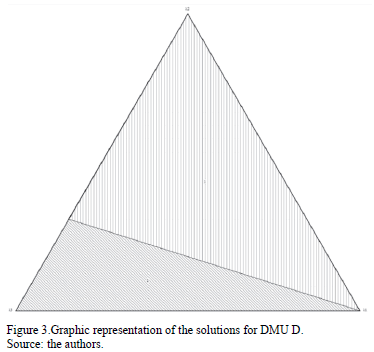
The targets obtained by f =1 are the same targets provided by the Banker and Morey model (1). Such targets are shown in bold. We shall note that for DMUs E and G, the Banker and Morey target is not present in the set of targets. This is due to the fact that the set of targets found by TRIMAP are limited to the extreme points. We can use other types of software to find other targets in the efficient frontier. For DMU D, the TRIMAP graphic solution is shown in Fig. 3. For a complete interpretation of TRIMAP graphic results with DEA models see Soares de Mello et al. [30].

This Fig. 3 shows the graphic representation of the indifference regions for each basic solution. All solutions contain l₁ vertex, due to the fact that this vertex corresponds to the non-discretionary variable, which cannot be changed.

We have to point out that the set of targets found by TRIMAP are limited to the extreme point. To obtain Banker and Morey's model results, we have solved their model for DMUs E and G. For DMU E, the model is presented in (11).

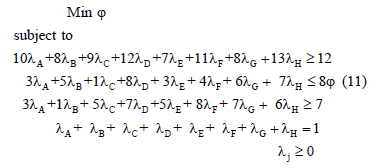
For DMUs E and G, the results are in Table 3.

To obtain the same results using model MORO-D-ND (model (6) with restriction (7)), we would have to introduce the restriction f=1. This clearly shows that the Morey and Banker solutions are dominated by one of the solutions obtained using TRIMAP.

 

5. Final comments

In this paper, we have presented a multiobjective approach to DEA models with non-discretionary variables. For efficient DMUs, all objective functions equal 1. For inefficient DMUs, we have obtained a set of targets instead of a single target.

We used the TRIMAP to find the results for the multiobjective models, as this method only finds extreme-efficient solutions. For other targets, other methods can be used, such as interactive methods [31,32] to find a suitable solution for the DMU.

However, the use of non-discretionary variables provides more realistic targets for the inefficient DMUs. As each inefficient DMU has more than one target, decision-makers may choose the the most suitable target among them.

Another advantage of the model proposed in this paper when compared with the Banker and Morey model is that, due to the multiobjective approach of the formulation, in our model the targets are also Pareto efficient.

 

Acknowledgements

We would like to thank CNPq and FAPERJ for their financial support.

 

References

[1] Charnes, A., Cooper, W.W. and Rhodes, E., Measuring the efficiency of decision-making units, European Journal of Operational Research, 2, pp. 429-444, 1978. DOI: 10.1016/0377-2217(78)90138-8        [ Links ]

[2] Patricia, G. and Pellicer, E., Organizational eficiency of consulting engineering firms: Proposal of a performance indicator, DYNA, 76(160), pp. 17-26, 2009.         [ Links ]

[3] Thanassoulis, E. and Dyson, R.G., Estimating preferred target input-output levels using Data Envelopment Analysis, European Journal of Operational Research, 56, pp. 80-97, 1992. DOI: 10.1016/0377-2217(92)90294-J        [ Links ]

[4] Zhu, J., Data envelopment analysis with preference structure, Journal of the Operational Research Society, 47, pp. 136-150, 1996. DOI: 10.2307/2584258, DOI: 10.1057/jors.1996.12        [ Links ]

[5] Lins, M.P.E., Angulo-Meza, L., and Moreira-da Silva, A.C., A multi-objective approach to determine alternative targets in data envelopment analysis, Journal of the Operational Research Society, 55, pp. 1090-1101, 2004. DOI: 10.1057/palgrave.jors.2601788        [ Links ]

[6] Quariguasi-Frota Neto, J. and Angulo-Meza, L., Alternative targets for data envelopment analysis through multi-objective linear programming: Rio de Janeiro Odontological Public Health System Case Study, Journal of the Operational Research Society, 58, pp. 865-873, 2007. DOI: 10.1057/palgrave.jors.2602216        [ Links ]

[7] Banker, R.D. and Morey, R.C., Efficiency analysis for exogenously fixed inputs and outputs, Operations Research, 34, pp. 513-521, 1986. DOI: 10.1287/opre.34.4.513        [ Links ]

[8] Golany, B. and Roll, Y., Some extensions of techniques to handle non-discretionary factors in data envelopment analysis, Journal of Productivity Analysis, 4, pp. 419-432, 1993. DOI: 10.1007/BF01073549        [ Links ]

[9] Camanho, A.S., Portela, M.C. and Vaz, C.B., Efficiency analysis accounting for internal and external non-discretionary factors, Computers and Operations Research, 36, pp. 1591-1601, 2009. DOI: 10.1016/j.cor.2008.03.002        [ Links ]

[10] Estelle, S.M., Johnson, A.L. and Ruggiero, J., Three-stage DEA models for incorporating exogenous inputs, Computers and Operations Research, 37, pp. 1087-1090, 2010. DOI: 10.1016/j.cor.2009.09.015        [ Links ]

[11] Banker, R.D., Charnes, A. and Cooper, W.W., Some models for estimating technical scale inefficiencies in data envelopment analysis, Management Science, 30, pp. 1078-1092, 1984. DOI: 10.1287/mnsc.30.9.1078        [ Links ]

[12] Fonseca, A.B.d.M., Soares-de Mello, J.C.C.B., Gomes, E.G. and Angulo-Meza, L., Uniformization of frontiers in non-radial ZSG-DEA models: An application to airport revenues, Pesquisa Operacional, 30, pp. 175-193, 2010. DOI: 10.1590/S0101-74382010000100009        [ Links ]

[13] Soares-de Mello, J.C.C.B., Angulo-Meza, L. and Lacerda, F.G., A DEA model with a non discritionary variable for Olympic evaluation, Pesquisa Operacional, 32, pp. 21-29, 2012. DOI: 10.1590/S0101-74382012005000004        [ Links ]

[14] Cooper, W. W., Seiford, L., and Tone, K., Introduction to data envelopment analysis and its uses: with DEA-solver software and references. USA: Springer Science, 2006.         [ Links ]

[15] Syrjänen, M.J., Non-discretionary and discretionary factors and scale in data envelopment analysis, European Journal of Operational Research, 158, pp. 20-33, 2004. DOI: 10.1016/S0377-2217(03)00362-X        [ Links ]

[16] Fried, H.O., Schmidt, S.L. and Yaisawarng, S., Incorporating the operating environment into a nonparametric measure of technical efficiency, Journal of Productivity Analysis, 12, pp. 249-267, 1999. DOI: 10.1023/A:1007800306752        [ Links ]

[17] Fried, H.O., Lovell, C.A.K., Schmidt, S.L. and Yaisawarng, S., Accounting for environmental effects and statistical noise in data envelopment analysis, Journal of Productivity Analysis, 17, pp. 157-174, 2002. DOI: 10.1023/A:1013548723393        [ Links ]

[18] Daraio, C. and Simar, L., Introducing environmental variables in nonparametric frontier models: A probabilistic approach, Journal of Productivity Analysis, 24, pp. 93-121, 2005. DOI: 10.1007/s11123-005-3042-8        [ Links ]

[19] Daraio, C. and Simar, L., Advanced robust and nonparametric methods in efficiency analysis. Methodologies and Applications. New York: Springer, 2007.         [ Links ]

[20] Muñiz, M., Paradi, J., Ruggiero, J. and Yang, Z., Evaluating alternative DEA models used to control for non-discretionary inputs, Computers and Operations Research, 33, pp. 1173-1183, 2006. DOI: 10.1016/j.cor.2004.09.007        [ Links ]

[21] Gomes, E.G., Soares-de Mello, J.C.C.B., E Souza, G.D.S., Angulo Meza, L. and Mangabeira, J.A.D.C., Efficiency and sustainability assessment for a group of farmers in the Brazilian Amazon, Annals of Operations Research, 169, pp. 167-181, 2009. DOI: 10.1007/s10479-008-0390-6        [ Links ]

[22] Lima, V.S., Soares-de Mello, J.C.C.B. and Angulo-Meza, L., Cost-benefit analysis in selected air trips using a non parametric method, African Journal of Business Management, 5, pp. 9678-9685, 2011.         [ Links ]

[23] Soares-de Mello, J.C.C.B., Angulo-Meza, L., Gomes, E.G., Serapião, B.P. and Lins, M.P.E., Análise de envoltória de dados no estudo da eficiência e dos benchmarks para companhias aéreas brasileiras, Pesquisa Operacional, 23, pp. 325-345, 2003.         [ Links ]

[24] Clímaco, J.C.N., Soares-de Mello, J.C.C.B. and Angulo-Meza, L., Performance measurement - from DEA to MOLP, in Encyclopedia of Decision Making and Decision Support Technologies, Adam, F. and Humphreys, P., Eds., ed Pennsylvania: IGI Global, 2008.         [ Links ]

[25] Golany, B., An interactive MOLP procedure for the extension of DEA to Effectiveness Analysis, Journal of the Operational Research Society, 39, pp. 725-734, 1988. DOI: 10.2307/2583767, DOI: 10.1057/jors.1988.127        [ Links ]

[26] Angulo-Meza, L., Biondi-Neto, L., Soares-de Mello, J.C.C.B., Gomes, E.G. and Coelho, P.H.G., Free software for decision analysis a software package for data envelopment models, in ICEIS 2005 - Proceedings of the 7^th International Conference on Enterprise Information Systems, Miami, 2005, pp. 207-212.         [ Links ]

[27] Clímaco, J.C.N. and Antunes, C.H., TRIMAP - an interactive tricriteria linear programming package, Foundations of Control Engineering, 12, pp. 101-119, 1987.         [ Links ]

[28] Clímaco, J.C.N. and Antunes, C.H., Implementation of an user friendly software package - a guided tour of TRIMAP, Mathematical and Computer Modelling, 12, pp. 1299-1309, 1989. DOI: 10.1016/0895-7177(89)90369-5        [ Links ]

[29] Gomes Junior, S. F., Soares de Mello, J. C. C. B., and Angulo-Meza, L., "DEA nonradial efficiency based on vector properties," International Transactions in Operational Research, vol. 20, pp. 341-364, 2013".. DOI: 10.1111/itor.12000        [ Links ]

[30] Soares-de Mello, J.C.C.B., Clímaco, J.C.N. and Angulo-Meza, L., Efficiency evaluation of a small number of DMUS: An approach based on Li and Reeves's model, Pesquisa Operacional, 29, pp. 97-110, 2009. DOI: 10.1590/S0101-74382009000100005        [ Links ]

[31] Korhonen, P. and Wallenius, J., A Pareto race, Naval Research Logistics, 35, pp. 615-623, 1988. DOI: 10.1002/1520-6750(198812)35:6<615::AID-NAV3220350608>3.0.CO;2-K        [ Links ]

[32] Alves, M.J. and Climaco, J.C.N., A review of interactive methods for multiobjective integer and mixed-integer programming, European Journal of Operational Research, 180, pp. 99-115, 2007. DOI: 10.1016/j.ejor.2006.02.033        [ Links ]

 

L. Angulo-Meza, holds a degree in Operations Research Operational Investigación - Universidad Nacional Mayor de San Marcos (1996), a MSc. degree in Production Engineering from COPPE, Federal University of Rio de Janeiro, COPPE/UFRJ (1998) and a PhD. in Industrial Engineering from COPPE Federal University of Rio de Janeiro COPPE/UFRJ (2002). She is currently an associate professor at the Federal Fluminense University (UFF), Department of Production Engineering, Metallurgical Industrial School in Volta Redonda. She has a fellowship from the CNPq and FAPERJ's Young Scientist Program. She has conducted a post-doctoral internship at the Instituto Superior Técnico, Technical University of Lisbon. She has served as the head of the Production Engineering Department of Volta Redonda (VEP), and has experience in Production Engineering, with emphasis in Operations Research, acting on the following topics: Data envelopment analysis (DEA - Data Envelopment Analysis), Multiobjective Linear Programming, Neural Networks, Computational Implementations and Educational Evaluation. ORCID: 0000-0003-4557-0210

J.C.C.B. Soares-de Mello, is graduated in Mechanical Engineering from the Federal Fluminense University, Brazil (1981), MSc. in Mathematics from the Federal Fluminense University, Brazil (1987), and PhD. in Production Engineering from the Federal University of Rio de Janeiro, Brazil (2002). He has conducted post-doctoral internship at the Faculty of Economics, University of Coimbra in 2006 and senior internship at Instituto Superior Técnico, Technical University of Lisbon in 2012. He is currently an associate professor at the Universidade Federal Fluminense, Brazil. In the administrative area, he has served as department head at the UFF of Applied Mathematics, coordinator of the basic cycle of courses in engineering, and operations coordinator of the vestibular commission department. He is currently the deputy coordinator of the post-graduate program in Production Engineering. He has experience in Production Engineering, with emphasis in Data Envelopment Analysis, acting on the following topics: data envelopment analysis (DEA), multicriteria, educational assessment, air transport and sports evaluation. ORCID: 0000-0002-6507-2721

S.F. Gomes-Jr. holds a PhD. (2010) and Msc. (2006) in Production Engineering from Universidade Federal Fluminense, Brazil graduated in Civil Engineering from Universidade Federal Fluminense, Brazil (1995) and a degree in Mathematics from the Center for Distance Education of the State of Rio de Janeiro, Brazil (2005). He is currently an associate professor, State University Center-West Zone UEZO and a professor at Redeemer College. He has experience in production engineering, with emphasis in operations research, acting on the following subjects: mathematics, multicriteria, data envelopment analysis and education. ORCID: 0000-0002-8159-3965