Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.83 no.195 Medellín Jan./Feb. 2016
https://doi.org/10.15446/dyna.v83n195.46652
DOI: http://dx.doi.org/10.15446/dyna.v83n195.46652
Simultaneous dual true random numbers generator
Generador dual simultáneo de números verdaderamente aleatorios
Josué Aarón López-Leyva a & Arturo Arvizu-Mondragón b
a Departamento de Ingeniería, CETYS Universidad México, Ciudad de Ensenada, México. josue.lopez@cetys.mx
b División de física aplicada, Centro de Investigación Científica y de Educación Superior de Ensenada (CICESE) Ensenada, Baja California, México. arvizu@cicese.mx
Received: October 21th, 2014. Received in revised form: March 13th, 2015. Accepted: December 10th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
This paper details the design and implementation of a simultaneous dual true random numbers generator using only one laser and a digital signal processing system with a DE0 Nano FPGA. We implemented the random generator in such a way that a vacuum optical field will exist in our system. Taking advantage of the inherently random nature of the field, simultaneously quadrature components are measured in order to generate a truly random voltage signal. Also, we used a dynamical system of statistical analysis to eliminate any residual component of direct current on output voltage signal due to an (unavoidable) optical power imbalance in the optical system that was implemented. Finally, were measured the parameters of the auto-correlation and bias probability with values of 0.00010, 0002, respectively, which means that our system can be considered as a true random sequence generator capable of producing two sequences in an independent manner with a bit rate of up to 25 MHz.
Keywords: random sequences; vacuum states; quantum noise.
Resumen
Se presenta el diseño e implementación de un generador dual simultáneo de números verdaderamente aleatorios usando solamente un láser y un sistema de procesamiento digital de señales con FPGA Nano DE0. Implementamos el generador aleatorio de manera que exista un campo óptico de vacío en el sistema; aprovechando la naturaleza inherentemente aleatoria del campo, se miden simultáneamente sus componentes en cuadratura para generar una señal de voltaje verdaderamente aleatoria. Usamos un sistema dinámico de análisis estadístico cuyo objetivo es eliminar cualquier componente residual de corriente continua en la señal de voltaje, ocasionado por un (inevitable) desequilibrio de potencia óptica en el sistema óptico implementado. Se obtuvieron valores de los parámetros de la auto-correlación y el offset de probabilidad de 0,0001 y 0,0002, respectivamente, concluyendo que el sistema puede ser considerado como un verdadero generador de dos secuencias independientes aleatorias a una velocidad de transmisión de hasta 25 MHz.
Palabras clave: secuencias aleatorias; estados del vacío; ruido cuántico.
1. Introduction
Currently, it is very useful to have systems capable of generating random signals and random numbers for diverse fields of knowledge. There are numerous applications that require a Random Number Generator (RNG), such as cryptographic systems, wireless communication simulations, sweepstakes, statistical simulations, etc. Usually, the RNG systems require the configuration of a computer system (or digital control systems) to generate a final "random" digital sequence based on a complex mathematical function [1-4], like those used in various programming languages such as Java, PHP, Matlab, etc. Formally, these kinds of generators are called Pseudo Random Number Generators (PRNG) because they do not produce completely random sequences. Other generators are called True Random Number Generators (TRNG), also known as Hardware Random Number Generators (HRNG), which use a natural noisy signal that exists on the same system or may come from other systems as the noise is obtained from a particular electronic device (hardware) such as resistor, Zener diode, avalanche diode, etc. These generators use various noises present in the systems in order to obtain random sequences and random numbers. Another version of the same RNG systems is called Free Running Oscillator Random Number Generator (FRO-RNG), in which a random oscillatory signal serves as a source of truly random continuous values from which a final random binary signal will be obtained. Furthermore, there are also systems that generate truly random numbers by means of quantum noise and/or using the phase measurement of an optical signal; these systems fall into the following categories TRNG, PRNG- RNG and FRO-RNG [5]. However, there are some important considerations that must be taken into account in the generators mentioned above, for example the systems that use the Johnson noise as an excitation source are affected by temperature changes; different temperature values produce noisy signals with different amplitudes, therefore an accurate temperature control is required. In the case of the optical systems used to generate random sequences and signals, a control system for the optical intensity (i.e. the number of photons per observation time) is required as this information will be used in the photoreceiver stage [6-9]. If the optical intensity is not controlled it would be required to design and implement other schemes on the photoreceiver side in order to be able to work with a different number of photons. Furthermore, commonly in the TRNG systems only one sequence is generated; therefore, if two or more different random sequences are required, it is necessary to choose one or more of the following options:
- The more obvious alternative (and maybe the more expensive one) is to use two or more (as required) independent TRNG systems.
- Use an electronic demultiplexer (DEMUX) in combination with one TRNG system to generate as many sequences as desired; however, there is a trade-off between the rate and the number of sequences to be generated.
- Obtain the data from a randomized single input stream and store them in a large memory. After this a digital system should be used, such as a high speed FPGA (Field Programmable Gate Array), in order to generate as many independent random sequences, which are required through the different available ports on the FPGA. Obviously, the number of possible sequences generated will depend on the number of available ports and on the processing speed on the FPGA.
When optical systems are used in order to generate random sequences by means of their respective optical noises (such as the phase noise, the amplitude noise and/or the quantum noise), in combination with the optical coherent detection (specifically, the Balanced Homodyne Detection (BHD)), the optical power balance on the different paths of the BHD system is very important (although usually hard to get). This is because an inappropriate optical power balance may produce a saturation of its output signal. It is also necessary to control the DC component of the output voltage signal. In some cases, such control is undertaken by means of a capacitor, although this technique may produce a slight distortion over the output signal [10]. It is important to mention that the obvious way of detecting quantum noise is to directly input the light in a single photodetector and then to analyze the resulting photocurrent using an electronic spectrum analyzer. However, there are limitations such as electronic noise, AC response, efficiencies, power saturation, and saturation of the amplifiers etc. [11]. Because of this we have chosen an alternative: a simultaneous dual true random numbers generator based on the use of the simultaneous detection of the optical vacuum state quadratures that uses balanced homodyne detection. This technique takes advantage of the random nature of the vacuum fluctuations, and at the same time avoids and/or reduces the limitations previously mentioned. The complete system that is described in this paper has a dynamic statistical analysis system implemented in a FPGA DE0 Nano in order to control the DC component that appears because of a (hard to avoid in the practice) inadequate optical power balance. It should be noted that some preliminary results of this hybrid technique in the context of quantum cryptography systems with continuous variables (CV-QKD) has been previously reported on [15]; however, in the present paper we additionally present a detailed mathematical description of its operation as well as more general and conclusive results.
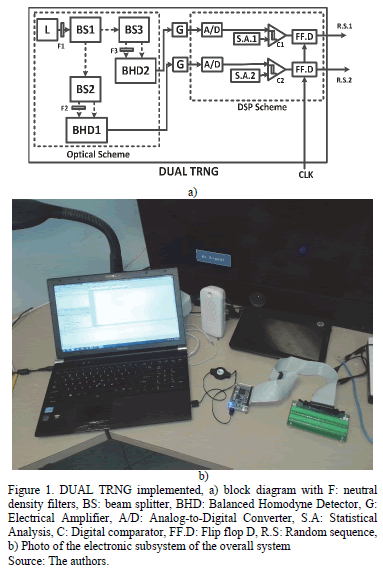
2. Generator implemented
The generator that was used consists of two fundamental stages: the optical subsystem and the digital signal processing subsystem that will be described below in more detail.
2.1. Optical subsystem
The generator that was used is shown in Fig. 1a) and 1b). It consists of a laser source and neutral density filters (F1) to adjust the variance of the detected quantum noise using shot noise units (because these units give us information about the quantum noise of the optical state) and to work in an optical power range acceptable for the BHDs. The laser produces an optical coherent state 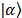 that is described by the following equation:
that is described by the following equation:

where 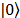 represents the vacuum state and
represents the vacuum state and 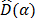 the displacement operator in order to generate the coherent state from the vacuum state. Roughly speaking, the vacuum state has a probability function that is described by the equation:
the displacement operator in order to generate the coherent state from the vacuum state. Roughly speaking, the vacuum state has a probability function that is described by the equation:
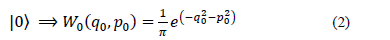
where 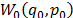 represents the Wigner function of the vacuum state in both quadrature components
represents the Wigner function of the vacuum state in both quadrature components 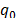 and
and 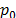 . Therefore, the probability function of the coherent state is:
. Therefore, the probability function of the coherent state is:
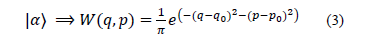
where 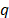 and
and 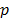 gives the average value of the number of photons.
gives the average value of the number of photons. 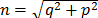 The optical power beam splitter 50/50 (BS1) is then used to produce the two signals (4) and (5) from which the two truly independent random binary sequences are generated.
The optical power beam splitter 50/50 (BS1) is then used to produce the two signals (4) and (5) from which the two truly independent random binary sequences are generated.
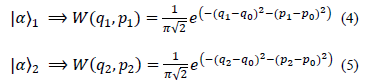
Then the beam splitters (BS2 50/50) and (BS3 50/50) produce two optical signals "balanced", due to the different optical path (fiber length) and optical devices; by adjusting a variable attenuator in one of the optical paths improves optical balance. In this way the marginal distribution functions (6) and (7) are obtained in each quadrature component:

Thus, the BHD1 and BHD2 generate two electrical output signals (8) and (9) that represent the quantum noise of the vacuum state in both quadrature components due to the unused port of the beam splitters according to the 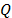 function of the optical quantum state [12].
function of the optical quantum state [12].


These electrical fluctuations are truly random and its bandwidth is determined by the BHDs bandwidth (5MHz for the BHDs used). Therefore, by using the quantum noise, two truly random signals are obtained.
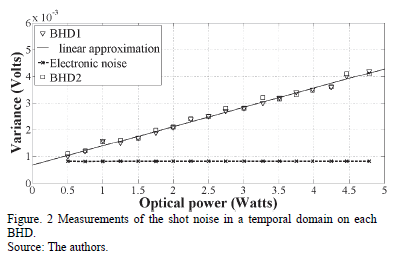
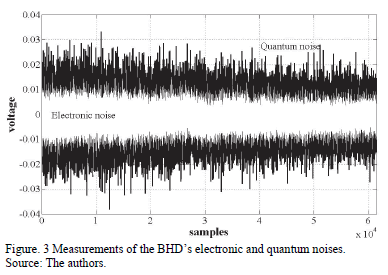
In order to know if the measured noise is really of a quantum nature (which is truly random), we must first determine if the implemented scheme is operating within the standard quantum limit (SQL, Standard Quantum Limit). One way of being sure of this is checking that the variance of the error signal holds a linear relation with the optical power of the laser; additionally it should be above the other noises. If the system is not working in the SQL, the BHDs measure other noises that are not necessarily of a random nature [5]. Fig. 2 shows the measures of the electronics and quantum noises in a time domain, where is possible determinate if the variance of the quantum noise is greater than the electronic noise. Fig. 3 shows the different variances of the quantum noise for different optical power.
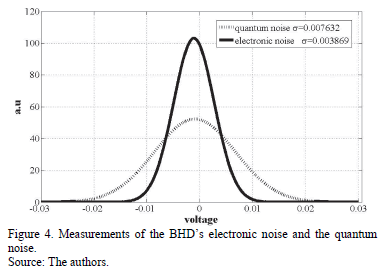
These signals are amplified (in our case, each BHD has a maximum gain of 30,000 V / V), and with this gain the noise values shown in Fig 3 and 4 were measured.
2.2. DSP subsystem
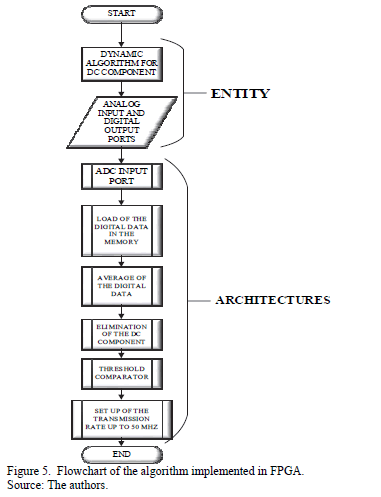
A Digital Signal Processing (DSP) subsystem based on the use of a DE0 Nano FPGA is used in order to digitize the electrical signal by means of an analog-to-digital 8-bits converter (ADC). An algorithm for dynamic statistical analysis that determines the average value of the analog random signal (due to a slight and hard to avoid optical imbalance) was implemented in VHDL. By using this analysis the reference signal (the threshold decision) is determined and used in order to generate a true random binary sequence. Furthermore a flip-flop D block (in VHDL) is used in order to vary the bit rate of the final binary sequence from 1 to 10 Mbps. This bit rate is determined by the FPGA clock (up to 50 MHz in our case). The algorithm flowchart is shown in Fig. 5. First, the programs set all the inputs and outputs variables in the entity of the VHDL. Next, many architectures are used in the same program to perform different tasks such as: a) ADC input ports (this stage converts the analog data into digital data for the next digital signal processing), b) Digital data load in the memory, (here the converted data are loaded in the internal memory of the FPGA), c) Digital data average, (in order to obtain the average value of the digital data that corresponds to the DC component), d) Threshold comparator, (in order to generate the final random binary sequence), and e) Setting of the transmission rate, (in order to change the bit rate of the final random binary sequence). Roughly speaking, a VHDL program was designed for a frequency divider in order to obtain a different transmission rate for the final sequence.
3. Test and measurement of the performance
As mentioned above for an adequate performance of our scheme, the measurement of the quantum noise is very important. One way to measure the quantum noise in such systems is through the variance of the photoelectric signal in the BHDs. The BS2 and BS3 send classical noise onto both BHD detectors and, thus, the photocurrents are correlated to each other. For quantum noise the effect of the beam splitter is different, i.e. the two resulting photocurrents are not correlated [11-13]. Fig. 3 presents the electronic noise measurements (white trace) and quantum noise (black trace) in the temporal domain in which is possible to distinguish the different variance values between them. However, because the setting of an adequate optical power is required, it will be necessary to change the optical power; the variance of the quantum noise also must also be modified. The probability function of the noises measured was shown in the Fig. 4. As can be seen in the figure, the variance (or standard deviation) of the quantum noise is greater than the variance of the electronic noise, which ensures that the experiment is working in the Standard Quantum Limit. In Fig. 2 we present the measurements for the quantum noise variance for different optical powers, and as expected, there is a linear dependence of the latter with the optical power. In this case, we used a laser with an average optical power of 5 mW. Thus, it was determined that the experiment was working at the standard quantum limit 18 dB above of the electronic noise. Measurements of quantum noise variance were performed by means of an oscilloscope with 50,000 samples at 4x109 samples/sec. The above behavior may be modeled using the following function, 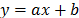 , where
, where 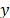 is the total noise in Volts (V),
is the total noise in Volts (V), 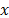 is the optical power of the local oscillator in watts (W),
is the optical power of the local oscillator in watts (W),  is a factor associated with the conversion factor of the photodetectors (in our case
is a factor associated with the conversion factor of the photodetectors (in our case  =0.66 V/mW),
=0.66 V/mW), 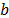 =0.8 mV is related to the electrical noise present in Volts. Thus, for an optical power of the local oscillator of 5 mW the r.m.s voltage is 4.35 mV. It is important to mention that the r.m.s voltage in a Gaussian density function with zero expected mean is equal to its variance. Therefore, an optical power of 5 mW in the local oscillator corresponds to a variance of 4.35 mV.
=0.8 mV is related to the electrical noise present in Volts. Thus, for an optical power of the local oscillator of 5 mW the r.m.s voltage is 4.35 mV. It is important to mention that the r.m.s voltage in a Gaussian density function with zero expected mean is equal to its variance. Therefore, an optical power of 5 mW in the local oscillator corresponds to a variance of 4.35 mV.
Regarding the performance of the system, there are fundamentally two parameters: the probability bias (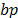 ) and the auto-correlation of the binary sequences generated. Sometimes, due to imperfections in measurement and hardware, the bits generated by an RNG system will contain a non-zero value of auto-correlation and probability bias, which may be minimized using the Von Neumann method [14]. Thus, the probability bias (
) and the auto-correlation of the binary sequences generated. Sometimes, due to imperfections in measurement and hardware, the bits generated by an RNG system will contain a non-zero value of auto-correlation and probability bias, which may be minimized using the Von Neumann method [14]. Thus, the probability bias (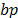 ) is defined as
) is defined as 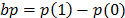 where
where 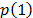 and
and 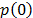 represent the probability of the binary values, 1 and 0, respectively, after having stored a large amount of bits. The best value would be bp=0 which means that the binary values are equiprobable; however, we must be sure that the value of autocorrelation is close to zero to ensure randomness [8]. The results obtained with our scheme show a value of
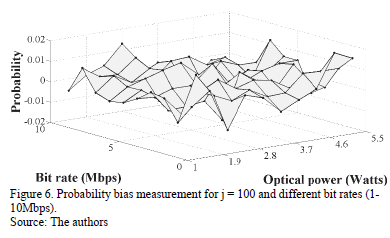
represent the probability of the binary values, 1 and 0, respectively, after having stored a large amount of bits. The best value would be bp=0 which means that the binary values are equiprobable; however, we must be sure that the value of autocorrelation is close to zero to ensure randomness [8]. The results obtained with our scheme show a value of 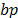 =0.0002. The Fig 6 shows the performance of
=0.0002. The Fig 6 shows the performance of 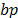 in a considerable observation time. As mentioned above, this value may be improved using the von Neumann method; however, in this case we considered that because we have obtained a very low value, an improvement was not required. Regarding the measurement of the discrete-time autocorrelation
in a considerable observation time. As mentioned above, this value may be improved using the von Neumann method; however, in this case we considered that because we have obtained a very low value, an improvement was not required. Regarding the measurement of the discrete-time autocorrelation 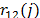 of the binary sequence, we used the equation (10) in which
of the binary sequence, we used the equation (10) in which 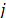 is the lag between the sequences
is the lag between the sequences 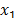 and
and 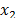 that are analyzed with a length
that are analyzed with a length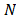 . Thus
. Thus 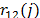 is defined as:
is defined as:
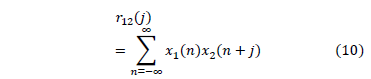
Then, the equation (10) is normalized and we obtain the equation:
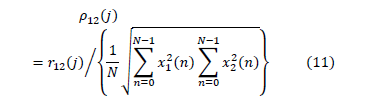
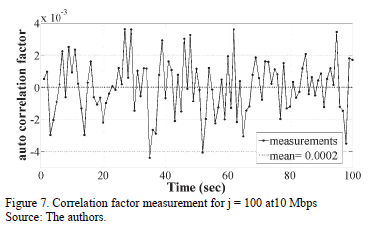
The overall system performance may be obtained through the probability bias and autocorrelation values. In order to do this we performed measurements of up to 10 Mbps with different optical powers. By varying the optical power it is possible to show that the system of statistical analysis is capable of working adequately even if the variance of the quantum noise has variations. The Figs. 6 and 7 show that the values of probability bias and autocorrelation are 0.0002 and 0.0001 respectively to measure ranges from 1 to 5 mW and from 1 to 10 Mbps.
3. Conclusions
This work presents a mathematical description, and the design and implementation of a True Random Numbers Generator based on a system that simultaneously measures both quadrature components of an optical field (the vacuum state) and also uses a dynamic statistical analysis. As mentioned above, some preliminary results of this hybrid technique in the context of quantum cryptography systems with continuous variables (CV-QKD) have previously been reported on [15]. However, in this paper we have presented more general and conclusive results in terms of the mathematical model and the development of a generator suitable to be used in different applications such as cryptographic systems (already mentioned), simulations, sweepstakes, etc., using the concepts of modern photonics [16]. In the system developed, the transmission rate of the final sequences may be independently configured for different simultaneous applications. In our experimental set-up we were able to get adequate values (to assure the randomness of the signals generated) of probability bias (0.0002) and autocorrelation (0.0001) for a bit rate of up to 10 Mbps. The bit rate obtained depends on the bandwidth of the BHDs and DSP subsystem used. Therefore, implementing a system with a higher rate is possible by means of changing such subsystems ( there are currently BHDs capable of operating on the order of the GHz as well as FPGAs and DSPs that have very high processing speeds).
Acknowledgments
The authors wish to thank the support they were given from CETYS University and CICESE Research Center. This work was supported by a CONACYT Basic Science Grant.
References
[1] Blaner, B., Abali, B. Bass, B.M., Chari, S., Kalla, R., Kunkel, S., Lauricella, K., Leavens, R., Reilly, J.J. and Sandon, P.A., IBM POWER7+ processor on-chip accelerators for cryptography and active memory expansion, IBM Journal of Research and Development, 57(6), pp.1-16, 2013. DOI: 10.1147/JRD.2013.2280090 [ Links ]
[2] Francillon, A. and Castelluccia, C., TinyRNG. A cryptographic random number generator for wireless sensors network nodes. 5th International Symposium on Modeling and Optimization in Mobile, Ad Hoc and Wireless Networks and Workshops, [Online]. pp. 1-7. Limassol. 2007. Available at: DOI: 10.1109/WIOPT.2007.4480051 [ Links ]
[3] Yang M., Guo, Q. and Wang, Z., A random number generator based software channel simulator for land mobile satellite channel. International Conference on Wireless Communications, Networking and Mobile Computing. pp. 1095-1098 Shanghai. 2007. DOI: 10.1109/WICOM.2007.280 [ Links ]
[4] Chen, I,-T., Tsai, J.-M. and Tzeng, J., Audio random number generator and its application. International Conference on Machine Learning and Cybernetics (ICMLC), pp.1678-1683. Guilin. 2011. DOI: 10.1109/ICMLC.2011.6017002 [ Links ]
[5] Stipcevic, M., Quantum random number generators and their use in cryptography, MIPRO Proceedings of the 34th International Convention, [Online]. pp. 1474-1479, 2011. Available at: http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=1354136 [ Links ]
[6] Zhu, Y., He, G. and Zeng, G,. Unbiased quantum random generator based on squeezed vacuum state. Int. J. Quantum Inform., [Online]. 10(1), pp. 1-13, 2012. Available at: http://www.worldscientific.com/doi/abs/10.1142/S0219749912500128 [ Links ]
[7] Stipčevića, M. and Medved-Rogina, B., Quantum random number generator based on photonic emission in semiconductors, Review of scientific instrument, [Online]. 78, pp. 1-7, 2007. Available at: http://scitation.aip.org/content/aip/journal/rsi/78/4/10.1063/1.2720728 [ Links ]
[8] Fürst, H., Weier, H., Nauerth, S., Marangon, D.G., Kurtsiefer, C. and Weinfurter, H., High speed optical quantum random number generation, Optics Express. 18(12), pp. 13029-13037. 2010. DOI: 10.1364/OE.18.013029 [ Links ]
[9] Wayne, M.A. and Kwiat, P.G., Low-bias high-speed quantum random number generator via shaped optical pulses, Optics Express, 18(8), pp. 9351-9357, 2010. DOI: 10.1364/OE.18.009351 [ Links ]
[10] Sanford-Williams C.R., Optoelectronic experiments on random bit generators and coupled dynamical systems. PhD thesis. Department of Physics, University of Maryland, USA, 2013. [ Links ]
[11] Bachor, H.A. and Ralph, T.C., A guide to experiments in quantum optics. Wiley VCH., [Online] Chapter 8, 2004. Available at: http://onlinelibrary.wiley.com/book/10.1002/9783527619238 [ Links ]
[12] E. Ip, et al., Coherent detection in optical fiber systems, Optics Express, 16(2), pp. 753-791, 2008. DOI: 10.1364/OE.16.000753 [ Links ]
[13] Yuen, H.P. and Chan, V.W.S., Noise in homodyne and heterodyne detection. Optics letters. 8(3), pp.177-179, 1983. DOI: 10.1364/OL.8.000177 [ Links ]
[14] Abbott, A.A. and Calude, C.S., Von Neumann normalisation of a quantum random number generator, Journal of Computability, [Online]. 1(1), pp. 59-83, 2012. Available at: http://content.iospress.com/articles/computability/com001 [ Links ]
[15] Lopez, J.A., Dual quantum random number generator using a FPGA for QKD-CV systems: Preliminary results. International Journal of Emerging Research in Management &Technology, [Online]. 3(6), pp. 6-8.2014. Available at: http://www.ermt.net/docs/papers/Volume_3/6_June2014/V3N6-138.pdf [ Links ]
[16] Martin-Pereda, J.A., La fotónica: Ayer y mañana. Revista Dyna Ingeniería e Industria, 89, pp.501-503. 2015. DOI: 10.6036/7116 [ Links ]
J.A. Lopez-Leyva, obtained his BSc. degree with an emphasis on Telecommunications from the Superior Technology Institute of Cajeme (ITESCA) in Sonora Mexico. From 2006 to 2008 he worked on Networking and Telephony projects. Finally, he obtained his PhD. in quantum communication using satellites and quantum cryptography at the CICESE Research Center in Baja California, Mexico. His current research interests include free space optical communications, Coherent optical communications, optical networks, statistical signal processing and quantum cryptography systems. ORCID-ID: 0000-0002-3004-5686
Arturo Arvizu-Mondragón, received his BSc. and MSc. degrees in Electronics in 1985 and 1990, respectively, from the Universidad Nacional Autónoma de México, Mexico and his PhD. in Telecommunications in 2000, from the CICESE Research Center, Ensenada, BC, Mexico. In 1987 he joined the Institute of Electrical Research, Cuernavaca, Morelos, México, working on projects relating to the optical and optoelectronics communications systems that are applied in power generation systems, and laboratories to test, measure and characterize electrical systems. In 1992 he joined the CICESE Research Center where he currently works in the fields of quantum communications, optical fiber and optical wireless communications with coherent detection. In 2000 and 2001 worked in a post-doctoral position in the telecommunications department at the École nationale supérieure des télécommunications, Paris, France. ORCID-ID: 0000-0001-6926-2197