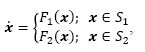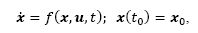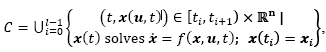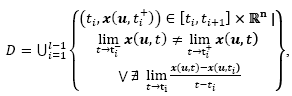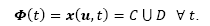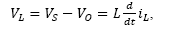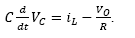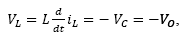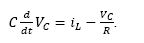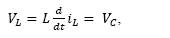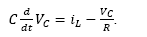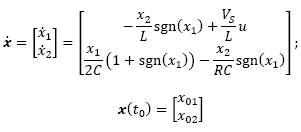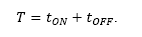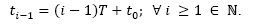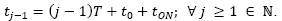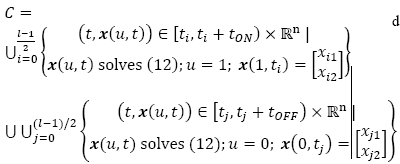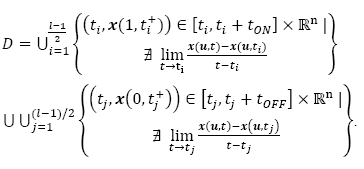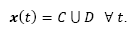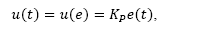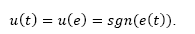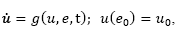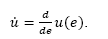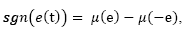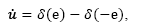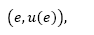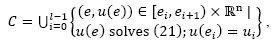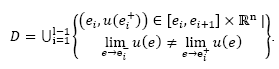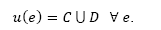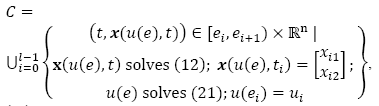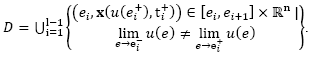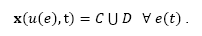1. Introduction
Dynamical systems when thought as operating under realistic conditions are usually constrained to evolve inside delimited zones of the state-space, as a natural consequence of physical limitations appearing by implementations, such as the saturation of actuation components and the boundaries of motion trajectories. Moreover, different operational modes of the system define particular regions in the solution space and therefore, a conditioned representation of the dynamics. Such interaction of continuous behavior and discrete transition-rules between operation modes is defined in terms of the so-called Hybrid Dynamical Systems (HDS).
An HDS can be stated as one with solution trajectories composed of continuous paths linked by discontinuous transitions obeying a discrete rule [1]. Hybrid models can be employed as simplified representations of complex systems [2-4] by taking advantage of the information reduction provided by discrete domains (e.g. the bouncing-ball system). Then, an HDS is the best way to describe the coupling between the continuous nature of physical systems and the discrete fashion of computations; i.e. a Cyber-Physical System (CPS), as topic of current research interest for development of intelligent computational systems interacting with nature [5,6]. On the other hand, it is necessary to design more efficient engineering systems in terms of energy consumption, as consequence of an increasing power demand under limited resources [2,7,8]. In particular, for the case of electrical systems it is well known the role of a power converter circuit for delivering to the load, in an efficient manner, the energy stored in a power supply (i.e. with a minimum loss) [9,10]. The operation of a power converter circuit is determined by the commutation pattern of the switching devices in the corresponding circuit topology. Pulse-width modulated signals (PWM) are often employed to accomplish this task. In a PWM-generation block the input is a continuous signal corresponding to the duty cycle, and the output is a discrete signal with only two possible values: ON or OFF [11,12]. Such a feature imposes a discrete change over the continuous nature of an electric circuit, allowing to model the power converter as a hybrid system [1,12]. To model a power converter is, in general, a complicated task given the discontinuities induced by switching devices [13,14]. Nevertheless, there are several works in the literature proposing isolated models for the converter and the control laws [15-18]. This paper shows a general definition for the hybrid system in terms of a set of continuous and discrete components, being applied to link the power converter and a simple control law, in an attempt to model and to explain the behavior of the controlled circuit, as an HDS. The contents of the paper are organized as follows: Section 2 introduces the hybrid dynamical systems and a set-based formulation for modelling its dynamics; Section 3 uses the proposed approach to model a power converter circuit; in Section 4 the hybrid modelling is extended to an On-Off controller being, furthermore, linked to the converter circuit; finally, Section 5 presents numerical validation of the models and discussion of results, with general conclusions given in section 6.
2. Hybrid Dynamical Systems HDS
Hybrid Dynamical Systems (HDS) have been a subject of increasing interest from the earlier developments in the Eastern literature till nowadays. In particular, new methodologies and techniques for analysis and control tasks appeared in an attempt to deal with the impossibility to apply the well-developed classical theory of smooth-dynamical systems. Interested readers are referred to [19] for a deeper review on some developments concerning piecewise-smooth dynamical systems (including hybrid systems) and applications.
As a representative example, let us consider the dynamical system described by:
with F1 and F2 representing two different modes of operation across the discontinuity boundary Σ in Fig. 1 (where the solution space S has been partitioned into S1 and S2), generating respectively the flow paths (1 and (2 .
Then in order to solve (1) for an arbitrary time t > 0, we must be able to detect accurately the crossing instants of the system flow through the boundary Σ for an appropriate commutation of the vector fields F. In general, it is not straightforward to find closed-form analytical solutions for these kinds of trajectory, moreover, when the boundary conditions may include discontinuities in the resulting flow. As a valid resource, numerical approximations of the trajectories are considered by appropriate formulations of automata resembling conditionals and transitions between discrete and continuous states. Synthesis and conditioning of numerical methods are then of remarkable importance in the analysis of hybrid dynamics. See [20] and references therein for a detailed description of event-driven simulators applied to systems with discontinuous flows.
2.1. A set-based formulation for the hybrid automaton
In general, a dynamical system given by:
where x is the state-vector of n state-variables, ƒ (.) is a continuous function (non-necessarily linear) of the states, u is a vector of allowed inputs and x 0 is a set of initial conditions; can be solved as a trajectory in the state space Φ(t) = x(t).
In an HDS such flow path Φ(t) can be described in terms of a combination of continuous sets of points, linked to discrete conditions between them; i.e. by considering the ordered pair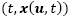 , each point of the state-space for the solution path Φ(t) belongs exclusively to any of both, a continuous set C defined by:
, each point of the state-space for the solution path Φ(t) belongs exclusively to any of both, a continuous set C defined by:
where 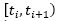 represents the
ith
interval of the domain where x(t) is smooth for l continuous trajectories; or the discrete set D:
represents the
ith
interval of the domain where x(t) is smooth for l continuous trajectories; or the discrete set D:
where 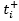 and
and 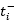 stand respectively for the infinitesimals of time just after and before the discrete transition at
ti
.
stand respectively for the infinitesimals of time just after and before the discrete transition at
ti
.
Hence, the total hybrid trajectory can be stated as:
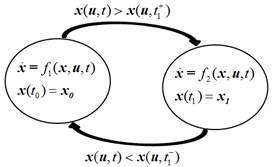
Such a result is illustrated in Fig. 2 for n = 2. Notice that it graphically explains, by an automaton, the situation depicted previously in Fig. 1. Then, the system jumps from the descriptions of the vector fields 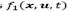 and
and 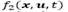 depending on the event occurring at;
depending on the event occurring at; 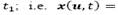 .
. 
The mathematical representation of HDS introduced here, will be employed in the following to describe the dynamic behavior of a power converter circuit.
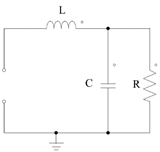
3. A Buck type power converter circuit
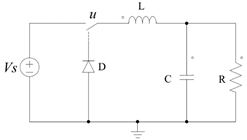
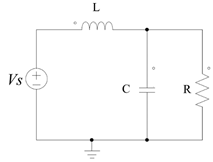
Fig. 3, shows the general circuit describing a buck DC-DC power converter. The operation of the system can be split in two modes depending on the conduction state of the MOSFET transistor which operates as a switch. Let us first consider the operational mode of conduction (u = 1).
The equivalent circuit is depicted in Fig. 4. As it can be seen, the source applies the power input to the load. Equations (6) and (7) describe respectively, the Kirchhoff's Voltage (KVL) and Current (KCL) laws applied to the circuit, where V 0 represents the output voltage in the load and VL , VC the corresponding to inductor and capacitor devices.
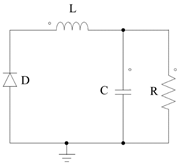
In the second mode, the switch is open (u =0) and then the energy stored in the capacitor and the inductor should supply the load temporarily until the next conduction mode occurs. Nevertheless, it is necessary to take into account the influence of the diode into the circuit. Hence, Fig. 5 shows the equivalent circuit when the diode is forward-biased ( iL >0), with eq. (8)-(9) representing its KVL and KCL equations.
On the other hand, Fig. 6 shows the non-conduction mode when the diode is reverse-biased. eq. (10)-(11) represent the KVL and KCL equations for the corresponding circuit.
Then, after defining as state variables the current of the coil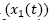 and the voltage of the load
and the voltage of the load 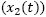 , it is possible to formulate a state-space representation of the circuit according to (2) by combining expressions (6)-(11) in the following matrix representation:
, it is possible to formulate a state-space representation of the circuit according to (2) by combining expressions (6)-(11) in the following matrix representation:
where 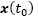 is the set of initial conditions.
is the set of initial conditions.
Notice that the signum function sgn(.) includes the discontinuity to the system flow and, therefore, an HDS representation of the model can be achieved easily, shown as follows.
3.1. A set-based formulation for the Buck circuit
The dynamics of the Buck-type power converter circuit depend on the pattern of the PWM signal, given that it provides the time instants where the command input u changes among its binary values.
In a more precise manner, each period T of the PWM signal is composed of an activation interval tON (for u = 1) followed by a gap of inactivity tOOF (for u = 0) i.e.
Hence, by starting from t =t0, the ith conduction instant can be defined as:
Also, the jth inactivity event can be stated by:
In accordance, the continuous set C describing the solution trajectory can be formulated as:
and equivalently, the discrete events are defined by:
In this way, it is possible to express the system flow, or solution trajectory, for the Buck-type converter circuit in eq. (12) by:
4. On-Off controller as a hybrid system
It is well known, that a proportional control action, defined by:
where e (t) represents the output error and KP constitutes the loop gain, is the most basic governing law that can be stated in a feedback control system. Moreover, if KP = 1 we have a unit gain negative feedback created naturally after closing the loop.
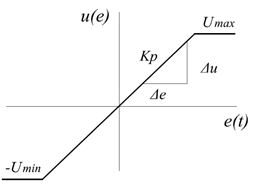
If KP is increased, the disturbance effects start to vanish and steady-state errors become diminished. In practice, however, the maximum value for this loop gain is constrained by saturation boundaries (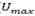 and
and 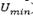 ) of signal levels as depicted in Fig. 7.
) of signal levels as depicted in Fig. 7.
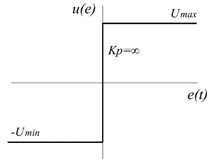
In spite of this, for higher values of the loop gain KP, the controller responses are strong enough to annihilate the error, with a limiting theoretical value of 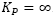 . The latter is the special case usually termed On-Off controller, a situation illustrated in Fig. 8 and described mathematically by:
. The latter is the special case usually termed On-Off controller, a situation illustrated in Fig. 8 and described mathematically by:
An On-Off controller delivers as control action, the maximum energy in a minimum time. There are several examples of practical applications for this kind of controller, including heat and cooling systems, level control and end-position control, among others.
As can be seen from (20), the controller has a discontinuous fashion that can be modelled as an HDS.
4.1. A set-based formulation for the On-Off controller
In accordance with (2), the dynamical representation of an On-Off controller of the form (20) can be stated as:
for 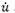 representing the rate of the control signal
representing the rate of the control signal 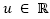 in terms of variations in
in terms of variations in 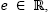 i.e.
i.e.
Then, by considering that a sgn(.) function can be expressed as the following sum of step functions µ(.):
equations (20), (22) and (23) can be combined to give:
by using the fact that the derivative of a step function µ(.) is a Dirac delta function δ(.).
Then, if dynamics of the On-Off controller (21) can be solved in terms of the ordered pair:
the continuous set C describing the flow path of the system is:
and the corresponding discrete events D are given by:
Therefore, the solution trajectory describing the On-Off control action can be stated as:
4.2. Hybrid formulation of the Buck circuit On-Off controlled
The sets proposed in section 2.1 for the continuous paths and discrete events composing the solution trajectory of hybrid systems, further applied in sections 3.1 and 4.1 to describe dynamics of a Buck-type power converter circuit and an On-Off controller, can be merged here to define the hybrid controlled circuit.
In essence, the two models can be coupled by considering that the time instants governing the commutation changes in the circuit, coincide with the zero crossing of the error signal, i.e. by combining equations (16) and (26), the continuous set C describing the flow path of the controlled circuit is:
and equivalently, by combining (17) and (26) the discrete events are defined by:
Finally, the flow-path of the controlled system can be stated by:
5. Numerical verification of the hybrid models and discussion
The analytic results shown in previous sections have been tested by comparing numerical evaluation of the proposed sets, with results of the commercial circuit simulation package OrCAD-Cadence®.
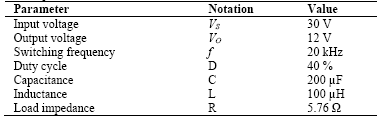
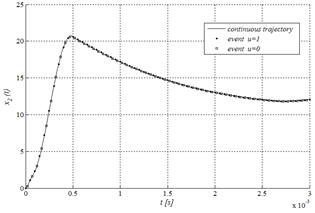
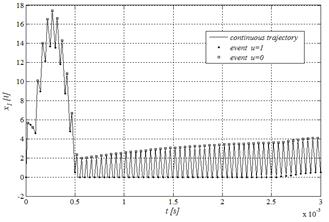
Figs. 9, 11 show the numerical evaluation in MATLAB® of the data sets given by eq. (18), as solution trajectories of the Buck-type converter circuit, for the parameter values listed in Table 1.
Source: Authors
Figure 9 Output voltage of a Buck-type power converter reproduced by numerical evaluation in MATLAB® of the hybrid model.
Source: Authors
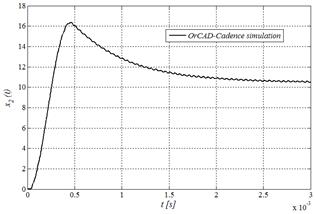
Figure 10 Output voltage of a Buck-type power converter reproduced by numerical simulation in OrCAD-Cadence®.
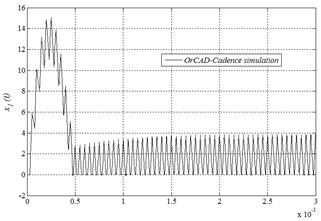
In comparison, Figs. 10, 12 reproduce equivalent results by employing OrCAD-Cadence®.
As can be noticed, the qualitative behavior of the voltage and current signals is replicated in both simulation environments. In particular, a smooth shape for the capacitor voltage is achieved with a peak time around 0.5[s] and a falling slope reaching a steady state regime close to the expected value of 12 [V] near to 3 [ms].
In contrast, the behavior of the inductor current is characterized by a discontinuous shape with an initial lobe followed by a stable average of around 2 [A] starting close to 0.5 [s].
However, there are also qualitative disagreements in the results that can be explained by special features added to the commercial circuit simulator (e.g. temperature dependence, non-idealization of circuit elements), not considered in our simple approach. Nevertheless, the agreement achieved is good enough to validate the correctness of the proposed scheme to model the dynamic behavior of the Buck-type power converter circuit as an HDS.
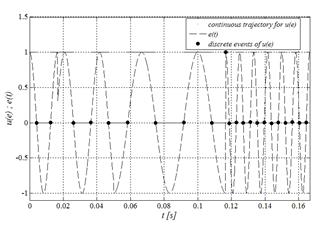
Now, in order to verify the hybrid model of the On-Off controller, Fig. 13 shows the synthesis in MATLAB® of a control signal u(t) = u(e), obtained by applying a predefined error waveform e(t) to the system.
Source: Authors
Figure 11 Inductor current of a Buck-type power converter reproduced by numerical evaluation in MATLAB® of the hybrid model.
Source: Authors
Figure 12 Inductor current of a Buck-type power converter reproduced by numerical simulation in OrCAD-Cadence®.
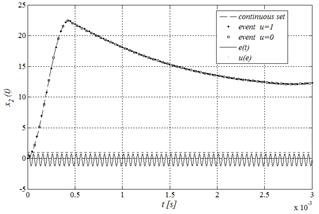
The same principle is employed in Fig. 14 to reproduce artificially in MATLAB® the output voltage signal of Fig. 9, by numerical evaluation of the data sets given by eq. (31), as solution trajectories of the Buck-type converter circuit when controlled by the hybrid On-Off action.
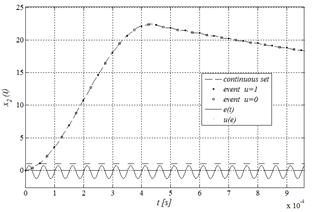
In such a case, the error signal applied to the controller as input, has a constant frequency and duty cycle values in accordance to the nominal values illustrated in Table 1. A detail of the waveform generated is illustrated in Fig. 15.
6. Conclusions
An HDS can be represented in terms of a trajectory composed of continuous paths linked by discrete events. Those continuous and discrete intervals have been defined by sets including all the possible points in the state-space which, belonging to the system-flow solutions, can be classified as part of one of the hybrid components.
Source: Authors
Figure 13 Input-output relationship of On-Off hybrid controller reproduced numerically in MATLAB®.
Source: Authors
Figure 14 Output voltage of Buck-type converter synthetized by numerical evaluation in MATLAB® of the hybrid model proposed for the controlled circuit.
Source: Authors
Figure 15 Detail for the output voltage of Buck-type converter synthetized in MATLAB® for the hybrid model proposed.
A Buck-type power converter circuit has been shown as an example of HDS in terms of the proposed set-based formulation. Numerical evaluation of the hybrid scheme allowed to verify the agreement for capturing the main dynamical features of the system responses compared with a reference framework given by a commercial circuit simulator package.
The proposed set-based approach has been further employed to define an On-Off controller as HDS. In such a case, the dynamics of the control signal at the output of the system was described in terms of variations on the error signal.
An approximation for the On-Off controlled Buck-type power converter circuit was then performed by merging the individual representations. As a result, the time instants corresponding to the events where the continuous flow of the circuit solution jumps discontinuously to the next continuous interval, correspond with the zero crossings of the error signal applied as input of the controller.
The numerical results obtained with the commercial circuit simulator were replicated by evaluating the set-based formulation of the controlled circuit, constituting a valuable tool in the path to understand the dynamical behavior of discontinuous systems.
It is interesting to notice the way it was possible to express the behavior of the controlled system, as the union of sets describing individually the circuit and the controller dynamics. This can be understood as a new framework that complements existing approaches, such as finite state machines, Petri nets and Markovian models, by defining formal rules scalable onto more complex systems. The potential of the proposed approach can be exploited by exploring the wide possibilities offered by sets theory in order to describe and to formalize continuous and discrete formulations and interactions in between.
A natural evolution for the application case considered is the study of more complex topologies of power conversion systems, including more than a simple converter with more than a simple controller. This is part of the current ongoing work on which the proposed approach is being applied as a way to model hybrid dynamic behavior.