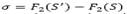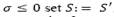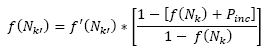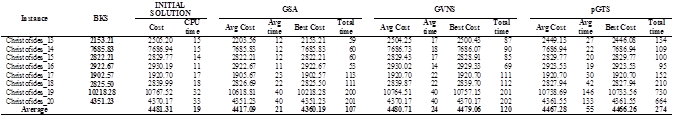1. Introduction
Long and short-term logistic operations consider Combinatorial Optimization Problems (COP). One of the most well studied decisions within the COP is the Traveling Salesman Problem (TSP), in which an agent should visit several cities and go back to its initial position in an optimal way minimizing the travelled distance and by considering that each city must visited only once. The problem could be represented by an undirected graph; where the vertex correspond to the cities and the arcs to the distances to be traveled satisfying the corresponding demand of cities [1]. The TSP is classified as NP-Hard problem, being computationally intractable with the number of nodes is increased [2,3].
The well-known Vehicle Routing Problem (VRP), is based on the principles of the TSP. Different variants of the Vehicle Routing Problem have been studied deeply in the fields of the Operations Research and Combinatorial Optimization, during the last fifty years. The variants include divided demand, time windows, different fleet, etc. The VRP could be depicted as a problem of designing routes from one depot to a set of customers by satisfying constrains of demand and of capacity of the vehicles. A variant of the VRP by considering several depots, from which is possible to satisfy the demand of the customers, each one of them having different fixed cost and different capacity, is a prominent research area [4,5]. This extension of the VRP is called Location-Routing Problems (LRP). The Location-Routing Problem considers two types of problems, which have been studied independently (the Multi Depot Vehicle Routing Problem - MDVRP and the Facility Location Problem - FLP). However, recent research results showed that the integration of both decisions allows obtaining a major efficiency of the design of the supply chain [6-8]. The FLP is associated with decisions of opening depots and assigning customers to the open depots. On the other hand, the MDVRP corresponds to the development of a set of routes to be performed by minimizing the total travelled distance. The LRPH is considered NP-hard, since it is a generalization of two well-known sub-problems: The Facility Location Problem (FLP) and the Multi-Depot Vehicle Routing Problem with Heterogeneous Fleet (MDHVRP) [4].
Exact algorithms for the LRP are proposed in [9]. In this work, Bender’s decomposition for splitting a LRP problem into two sub-problems (location-assignment and routing) is proposed. The drawback of linear programming approaches appears when dealing with real-life problems due to the cardinality of the scenario. Therefore, heuristic approaches are commonly used.
The heuristics algorithms for the LRP can be classified [6,7] into groups (sequential, iterative, nested) regarding to the way to deal with the FLP and the MDVRP. In the sequential approach, an algorithm for the MDVRP is performed after the FLP has been solved and, hence, there is no feedback between the two approaches. The iterative algorithm tries to take this drawback into account by iterating on the process. The nested algorithms compute the MDVRP for each solution obtained in the FLP. In general terms, sequential approaches tend to be faster than iterative and nested ones regarding the number of iterations to be performed.
One example of a sequential algorithm is the two-phase algorithm introduced in [10]. In the first phase, the FLP is solved by considering the length of the tours (routes) as a variable cost. In the second phase, a multilevel heuristic is used to solve the corresponding MDVRP. The proposed method in [11] is similar to the approach proposed by [10]. The main difference is that using a combined approach between a tabu search approach and a simulated annealing scheme solves the two phases. Another sequential algorithm based on four levels is considered in [12]. In this work, a combined problem by considering inventory decisions with a heterogeneous fleet is solved exactly by a mathematical model. Finally, a problem of transfer products from hubs to customers by considering a heterogeneous fleet is introduced in [13].
Typically, the LRP problems have considered an unlimited fleet of homogeneous vehicles. Although some considerations of heterogeneous fleet for the LRPH are proposed by [9-13], the literature regarding to location routing problems by considering heterogeneous fleet is scarce. Thus, this work is focused on the comparison of granular-based heuristic algorithm for solving the Location Routing Problem with Heterogeneous Fleet (LRPH). Indeed, the only work related to the LRPH has been introduced by Linfati et al [4]. In this paper, a modified granular tabu search for the LRPH has been proposed. The proposed algorithm is executed on instances adapted from the literature and the results are compared with a relaxed version of the proposed mathematical model for the LRPH. A remarkable fact of this algorithm is the use of the granularity concept introduced by [14], which is, in fact, a key for reducing the computational cost of the tabu search while conserving the quality of the solution. This paper aims to apply this idea to other heuristic algorithms in order to reduce the search space.
A work related to a similar problem of LRPH is presented in [15]. This paper considers a mathematical formulation and a Variable Neighborhood scheme for the Multi-Depot Vehicle Routing Problem with Heterogeneous Fleet (MDHVRP). Unlike the LRPH, the MDHVRP not considers decisions related to the depots to be opened.
In this work, we perform a computational comparison of three trajectory heuristics by using the granular concept introduced in [14] for the LRPH. The former algorithms consider the same initial solution obtained by a hybrid procedure and the same neighborhood structures. The first algorithm, called Granular Simulated Annealing approach (GSA), considers a Simulated Annealing (SA) method, with a ”granular” search space, to improve the initial solution S 0 [5]. The second algorithm, called Granular Variable Neighborhood Search (GVNS), considers a Variable Neighborhood Search (VNS) procedure to enhance the quality of solution S 0. Finally, the third algorithm, called Granular Tabu Search (pGTS), consider a Probabilistic Granular Tabu Search scheme for the LRPH.
The main contribution of the paper is the comparison of effective algorithms for the solution of the LRPH. The proposed algorithms are novel metaheuristic approach, which combine different local based procedures with a granular search space for getting good results within short computing times. The paper is structured as follows. Section 2 introduces the general framework used by the considered algorithms. A detailed description of the three approaches is given in Section 3. The comparative study on adapted benchmark instances from the literature is provided in Section 4. Finally, Section 5 contains concluding remarks.
2. General framework
2.1. Mathematical formulation
The LRPH could be represented by the following undirected graph problem: Let 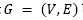 be a complete undirected graph, where
be a complete undirected graph, where 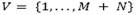 is the set of vertices representing customers and potential depots, and
is the set of vertices representing customers and potential depots, and 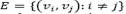 is the set of edges. Vertices
is the set of edges. Vertices 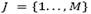 correspond to set of customers each with known positive demand di, and vertices
correspond to set of customers each with known positive demand di, and vertices 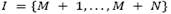 correspond to the potential depots, each with capacity wi and opening costs oi. With each edge
correspond to the potential depots, each with capacity wi and opening costs oi. With each edge 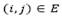 is associated a non-negative traveling cost
cij
. At each potential depot
is associated a non-negative traveling cost
cij
. At each potential depot 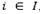 , a set of K heterogeneous vehicles is located, each with a vehicle capacity qk. Furthermore, any vehicle that performs a route generates a fixed cos vkt. The goal of LRPH is to determine the depots to be opened, the customers to be assigned to each open depot, and the routes to be performed to fulfill the demand of the customers by considering a heterogeneous fleet. Indeed, the LRPH integrates a strategic decision (depots to be used) and an operational decision (the routes to be developed by considering a heterogeneous fleet).
, a set of K heterogeneous vehicles is located, each with a vehicle capacity qk. Furthermore, any vehicle that performs a route generates a fixed cos vkt. The goal of LRPH is to determine the depots to be opened, the customers to be assigned to each open depot, and the routes to be performed to fulfill the demand of the customers by considering a heterogeneous fleet. Indeed, the LRPH integrates a strategic decision (depots to be used) and an operational decision (the routes to be developed by considering a heterogeneous fleet).
The objective function of LRPH considers the minimization of the sum of the fixed cost of the depots, of the costs of the used vehicles, and of the costs related with the distance traveled by the vehicles [4]. Any LRPH solution is feasible, if the following constraints are satisfied: (i) Each route starts and finishes at the same depot, (ii) each customer must visited exactly once by one vehicle, (iii) the sum of the demand of the customers served by a vehicle 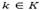 must not exceed its corresponding vehicle capacity
qk
, (iv) the sum of the demand of the customers assigned to an open depot
must not exceed its corresponding vehicle capacity
qk
, (iv) the sum of the demand of the customers assigned to an open depot 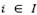 must not exceed its corresponding depot capacity
wi
, and (v) the flow of products between depots is not allowed.
must not exceed its corresponding depot capacity
wi
, and (v) the flow of products between depots is not allowed.
2.2. Concept of granular search space
The granular search conception (Toth and Vigo [14]), is predicated on the employment of a sparse graph (incomplete graph) containing the edges incident to the depots, the edges belonging to the best feasible solutions found so far, and the edges whose cost is smaller than a granularity threshold 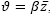 , where
, where 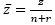 is the average cost of the edges belonging to the best solution found so far, and β is a dynamic sparsification factor which is updated during the search ([4-5] and [14]). In particular, the search starts by initializing β to a small value β
0. After
is the average cost of the edges belonging to the best solution found so far, and β is a dynamic sparsification factor which is updated during the search ([4-5] and [14]). In particular, the search starts by initializing β to a small value β
0. After 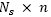 iterations the value of β is increased to the value
βn
, and / additional iterations are performed by considering as current solution the best feasible solution found so far [7]. Conclusively, the sparsification factor
β is reset to its previous value β
0 and the search continues. β
0, β
n, N
s, and N
r are given parameters. The main idea of the granularity is to obtain high quality solutions in based-trajectory heuristics within short computing times [6,7].
iterations the value of β is increased to the value
βn
, and / additional iterations are performed by considering as current solution the best feasible solution found so far [7]. Conclusively, the sparsification factor
β is reset to its previous value β
0 and the search continues. β
0, β
n, N
s, and N
r are given parameters. The main idea of the granularity is to obtain high quality solutions in based-trajectory heuristics within short computing times [6,7].
2.3. Neighborhood structures
The former heuristics use well-known intra-route (moves performed in a performed route) and well-known inter-route (moves performed between two routes assigned to the same depot or to different depots) moves corresponding to five neighborhood structures 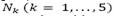 : Insertion, Swap, Two-opt, Double-Insertion, and Double-Swap [4-7]. A move is performed only if all the new inserted edges in the solution belonging to the sparse graph (granular search space).
: Insertion, Swap, Two-opt, Double-Insertion, and Double-Swap [4-7]. A move is performed only if all the new inserted edges in the solution belonging to the sparse graph (granular search space).
Some of the proposed approaches allow infeasible solutions respect to the depot and vehicle capacity constraints. For any feasible solution S, we calculate its objective function value 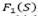 as the sum of the fixed cost of the depots, of the used vehicles and of the cost of the edges traveled by the performed routes. On the other hand, if the solution S is infeasible, we calculate its objective function value
as the sum of the fixed cost of the depots, of the used vehicles and of the cost of the edges traveled by the performed routes. On the other hand, if the solution S is infeasible, we calculate its objective function value 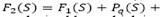
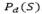 , where
, where 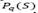 is a penalty term obtained by multiplying the global over vehicle capacity of the solution S times a dynamically updated penalty factor
is a penalty term obtained by multiplying the global over vehicle capacity of the solution S times a dynamically updated penalty factor 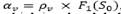 , and
, and 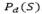 is a penalty term obtained by multiplying the global over depot capacity 𝑆 times a dynamically updated penalty factor
is a penalty term obtained by multiplying the global over depot capacity 𝑆 times a dynamically updated penalty factor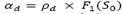 . In particular,
. In particular, 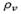 and
and 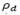 are adjusted parameters during the search, and
are adjusted parameters during the search, and 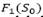 is the objective function value of the initial solution S
0
. If infeasible solutions with respect to the depot capacity have been not found over N
fact
iterations, then the value of
is the objective function value of the initial solution S
0
. If infeasible solutions with respect to the depot capacity have been not found over N
fact
iterations, then the value of 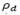 is set to
is set to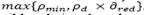 , where
, where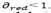 . On the other hand, if feasible solutions have been not found during N
fact
iterations, then the value of
. On the other hand, if feasible solutions have been not found during N
fact
iterations, then the value of 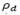 is set to,
is set to, 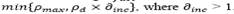 . A similar procedure is applied to update the value of
. A similar procedure is applied to update the value of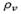 . Note if the current solution S is feasible,
. Note if the current solution S is feasible,  (for further details see [6-7]).
(for further details see [6-7]).
2.3. Initial Solution
Utilizing a hybrid heuristic based on a cluster approach, a good feasible initial solution 𝑆 0 is generated within short computing times. The following steps are executed until all the customers are assigned to one route and one depot:
Firstly, a giant TSP tour containing all the customers (without the consideration of the depots) is constructed by using the well-known Lin-Kernighan heuristic (LKH) ([16] and [17]). Secondly, starting from any initial customer 𝑗 ⋆ , divide the built giant TSP tour into several clusters composed of consecutive customers so that, for each cluster the vehicle capacity constraint is satisfied. In particular, we have assigned the large vehicles firstly.
Thirdly, for each depot 𝑖 and each cluster g, a TSP tour is obtained using procedure LKH to evaluate the traveling cost of the route performed starting from i and visiting all the customers belonging to g (keeping the sequence obtained by the giant TSP). Finally, the depots are assigned to the clusters by solving an ILP model for the Single Source Capacitated Facility Location problem. This step determines the depots to be opened and the clusters to be assigned to the open depots (for further details see [18] and [19]).
3. Description of the considered algorithms
3.1. The Granular Simulated Annealing heuristic algorithm (GSA)
The former algorithm considers a standard implementation of the Simulated Annealing metaheuristic (SA) by using a granular search space (reduced graph). We have assumed the same notation used on similar problems such as LRP [4]. Let S* be the best feasible solution found so far, S the current solution (feasible or infeasible), S’a random solution obtained from the neighborhood solutions of the current solution S, α the cooling factor, and 𝑇 the current temperature. Initially, we set 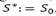 , and
, and 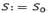 . In addition, we set the initial temperature T0 and the number of iterations
. In addition, we set the initial temperature T0 and the number of iterations 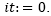 . The proposed algorithm performs the following steps until the number of iterations is reached:
. The proposed algorithm performs the following steps until the number of iterations is reached:
Decrease the current temperature every Ncool iterations (where Ncool is a given parameter) by using the following function 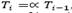 , where 0 < α < 1; and also increase the number of iterations
, where 0 < α < 1; and also increase the number of iterations 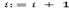 .
.
Construct a random solution S’ obtained by considering all the neighborhood structures 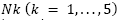 from the current solution S described in section 2.3.
from the current solution S described in section 2.3.
Generate a random number 𝑟 in the range [0, 1];
If  , set S: = S’; otherwise, keep S.
, set S: = S’; otherwise, keep S.
Finally, the best feasible solution found so far S* is kept. The pseudocode algorithm of GSA is presented as follows:

In particular, the GSA approach requires less computing effort performing more iterations respect to the other proposed approaches.
3.2. The Granular Variable Neighborhood Search approach (GVNS)
The GVNS algorithm brings together the potentiality of the systematic changes of neighborhood structures proposed by the well-known Variable Neighborhood Search (VNS) [20], and the efficient Granular Search Space introduced by [14] and improved by [5-7]. According to [20], the VNS applies a search strategy based on the systematic change of the neighborhoods structures to elude local optima. Three main concepts are applied on a VNS: (1) All the local minimum obtained by different neighborhood structures are not necessarily equals; (2) The best local minimum (respect to the objective function) obtained from all possible neighborhood structures (described in section 2.3) is called global minimum; (3) The different local minima obtained from the neighborhood structures should be relatively close each other.
Once the initial solution is performed (S0), the VNS approach iterates through different neighborhood structures to amend the best feasible solution (S*) found so far, until a the number of iterations is reached. The algorithm starts by setting 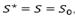 , where S is the current solution.
, where S is the current solution.
The Variable Neighborhood Search considers two steps: (1) selecting a random solution from the first neighborhood and (2) applying a Granular Search Space by the same exchange operator until there is no more improvement. Then, the algorithm selects another neighborhood and the search continues.
The pseudocode algorithm of GVNS is presented as follows:

Finally, the best feasible solution found so far S* is kept.
3.3. A probabilistic Granular Tabu Search heuristic algorithm (pGTS)
The proposed algorithm is an extension of the proposed idea by [21] for the DCVRP. After the construction of the initial solution So, the pGTS algorithm iterates through different neighborhood structures (described in Section 2.3) by using a discrete probabilistic function to improve the best feasible solution (S*) found so far, until the number of iterations is reached. The algorithm starts by setting 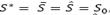 , where
, where 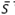 is the current solution (feasible or infeasible), and
is the current solution (feasible or infeasible), and 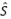 is the current feasible solution. The following steps then are repeated sequently. First, the former algorithm selects a neighborhood from the neighborhoods structures
is the current feasible solution. The following steps then are repeated sequently. First, the former algorithm selects a neighborhood from the neighborhoods structures 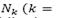
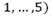 described in Section 2.3 by using the following function of probability
described in Section 2.3 by using the following function of probability 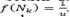 , where u is the total number of neighborhoods. Second, we apply a granular tabu search (GTS) based on the idea proposed by [14] in the selected neighborhood
, where u is the total number of neighborhoods. Second, we apply a granular tabu search (GTS) based on the idea proposed by [14] in the selected neighborhood 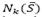 until a local minimum S’ is found. Depending on the solution, the following choices are possible:
until a local minimum S’ is found. Depending on the solution, the following choices are possible:
Increase the probability of selecting the current neighborhood (Nk) by a given factor Pinc as follow
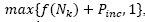 , only if any of three cases occurs: (1) S’is infeasible and
, only if any of three cases occurs: (1) S’is infeasible and 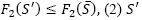 is feasible and
is feasible and 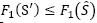 , and (3) S’ is feasible and
, and (3) S’ is feasible and 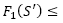
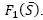 . If (1) is performed, then
. If (1) is performed, then 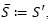 , if (2) is found, set
, if (2) is found, set 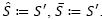 . Finally, if (3) occurs, set
. Finally, if (3) occurs, set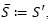 .
.Otherwise, decrease the probability of selecting the current neighborhood (Nk) by a factor Pdec as follow:
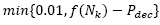 .
.
In order to preserve the probability function properties after decreasing or increasing a certain neighborhood, the values of the probability to select other neighborhoods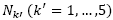 , where
, where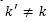 , must be adjusted [21]. If the probability to select the neighborhood Nk is decreased in a Pdec value, the remaining value
, must be adjusted [21]. If the probability to select the neighborhood Nk is decreased in a Pdec value, the remaining value 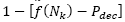 is distributed for the remaining neighborhoods according to their current (probability) [21]. Therefore, the new probability
is distributed for the remaining neighborhoods according to their current (probability) [21]. Therefore, the new probability  to select the remaining neighborhoods (
to select the remaining neighborhoods (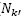 ) is calculated as follows:
) is calculated as follows:
where 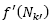 is the previous probability of the corresponding remaining neighborhood (
is the previous probability of the corresponding remaining neighborhood (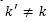 ). If the probability to select the neighborhood N
k
is increased in a P
inc
value, the remaining value
). If the probability to select the neighborhood N
k
is increased in a P
inc
value, the remaining value 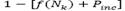 is distributed for the remaining neighborhoods according to their current (probability). Therefore, the new probability
is distributed for the remaining neighborhoods according to their current (probability). Therefore, the new probability 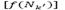 to select the remaining neighborhoods (
to select the remaining neighborhoods (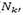 ) is calculated as:
) is calculated as:
Finally, the best feasible solution found so far S* is kept. The algorithm explores the solution space by moving at each iteration, from a solution  to the best solution in the neighborhood
to the best solution in the neighborhood 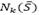 , even if it is infeasible. The selected move is declared as tabu. The tabu tenure is defined as a random integer value in the range
, even if it is infeasible. The selected move is declared as tabu. The tabu tenure is defined as a random integer value in the range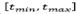 , where t
min
and t
max
are given parameters [21].
, where t
min
and t
max
are given parameters [21].
The pseudocode algorithm of pGTS is the following:
The pseudocode of the pGTS shows a brief summary of the performance of the proposed algorithm according to the discrete probability function and the replacement of the solutions depending of the characteristics of the solution found by the neighborhood S’.


4. Computational experiments
Fixing a maximum CPU time as stopping criterion has performed the comparison of the effects of the initial solution on the performance of the algorithms GSA, GVNS and pGTS. Finally, the best performance of the algorithms has been considered by executing 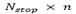 iterations (where
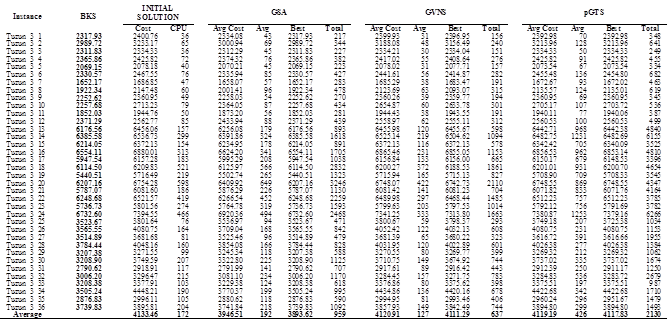
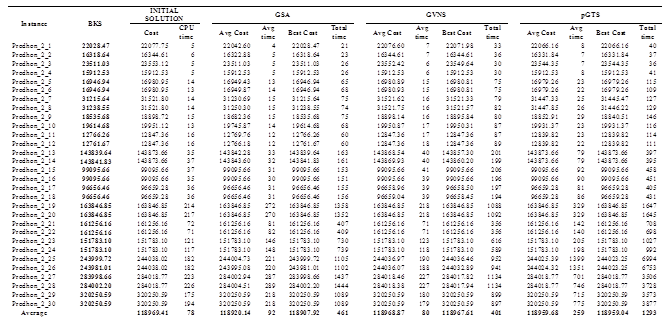
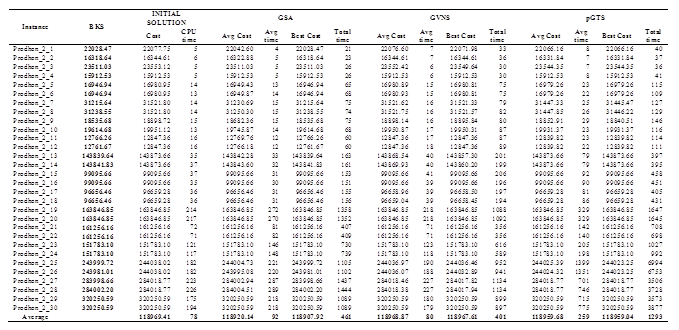
iterations (where 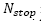 is a given parameter) for each instance. For each considered instance, the proposed approaches have been executed five times with different random generator seeds. The results reported in Tables 2 to 5 correspond for each instance to the best solution value obtained over the five runs with its corresponding total running time and the average results found within its corresponding computing time.
is a given parameter) for each instance. For each considered instance, the proposed approaches have been executed five times with different random generator seeds. The results reported in Tables 2 to 5 correspond for each instance to the best solution value obtained over the five runs with its corresponding total running time and the average results found within its corresponding computing time.
The three former algorithms have been coded in C++, and the computational experiments have been performed on an Intel Core Duo (only one core is used) CPU (2.00 GHz) under Linux Ubuntu 12.1 with 2 GB of memory RAM. The proposed algorithms have been tested on four benchmarking sets of instances adapted from the literature. The set of instances are available in https://github.com/maxbernal/LRPH. In all the sets, points in the plane represent the customers and the depot. Therefore, the traveling cost for an edge is calculated as the Euclidian distance between vertices.
The first three sets of instances are adapted from benchmarking instances for the CLRP proposed by [23], [24] and [25] for the CLRP respectively. In particular, for these sets of instances, the characteristics of the vehicles (fixed cost and capacities) have been modified in order to consider heterogeneous fleet for a location-routing problem. The first data subset was adapted from [23], and contains 36 instances with uncapacitated depots. The number of customers for each instance is n = 100, 150 or 200. The number of potential depots is either 10 or 20. The second data subset was adapted from [24], and considers 30 instances with capacity constraints on routes and depots. The number of customers for each instance is n = 20, 50, 100 or 200. The number of potential depots is either 5 or 10. Finally, the third data subset was adapted from [25], and considers 13 instances also with capacity constraints on depots and routes. The number of customers ranges from 21 to 150, and the number of potential depots from 5 to 10.
The fourth set is adapted from [26]. Originally, the instances from [26] are proposed for the HFVRP. In the HFVRP, all the depots are considered as opened in order to determine the routes to be performed. On the other hand, for the LRPH all the depots are considered as “potential”. Therefore, it is mandatory to select the depots to be opened and the customers to be assigned to each open depot.
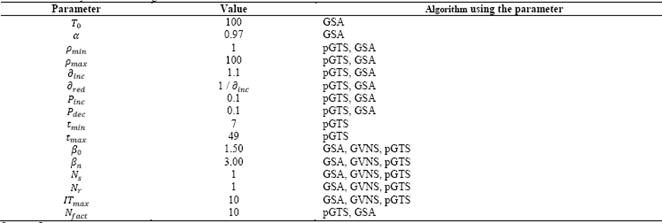
4.1. Setting of parameters
A suitable set of parameters, whose values are based on extensive computational tests on the benchmark instances, was selected for each algorithm. The parameters and values are presented in Table 1.
These values have been utilized for the comparison of the solutions obtained by the described algorithms.
The calibration of the value of each parameter was performed by a multi-objective optimization approach (considering the minimization of the objective function and the computing time). Values coming from previous works with similar algorithms ([4,5-7,21]) are used. The next step is to select a parameter and search for the given value the best result. This search is executed applying 1D function minimization. The process is carried out for each considered value. Since this process is iterative, it can be refined using more repetitions.
4.2. Comparison of the three described algorithms
For each instance, the proposed algorithms are executed 5 times due to their random calculations. Tables 2 - 5 provide the detailed results of the three proposed algorithms on the four data sets respectively. The algorithms are compared based on their best and average objective function for each instance; and the CPU for obtaining the best result and the CPU time to process the five runs of each instance. As expected, the GSA algorithm is faster, in the most of the cases, than the other algorithms since a solution is selected randomly and then evaluated; while GVNS performs local search on the selected solution, and pGTS explores the granular search space. A remarkable fact of the three algorithms is that although using random numbers, the objective function value tends to converge (see Tables 2 - 5).
The results clearly show that algorithm GSA outperforms the other two algorithms for what concerns both the CPU time and the quality of the answers found. Indeed, for all the data sets, the average costs, and the values of the best results for GSA are better than the corresponding values of algorithms GVNS and pGTS. Therefore algorithm GSA is the best performing of the three described algorithms, and, it could be compared with the most effective heuristics will publish in the literature.
5. Final remarks and future research
In this paper, a comparison of trajectory granular based algorithms for the Location Routing Problem with Heterogeneous Fleet (LRPH) is performed. All the proposed approaches use a granular search space based on the idea of using a sparse graph instead of the complete graph. Three algorithms have been proposed: Granular Simulated Annealing (GSA), Granular Variable Neighborhood Search (GVNS) and a probabilistic Granular Tabu Search (pGTS).
The computational experiments show that algorithm GSA generally obtains better results in terms of average and best results than those obtained by algorithms GVNS and pGTS. The results emphasize the importance of the granular search approach for the proposed algorithms, by showing that it significantly improves the performance and the computing time of the proposed approaches. We have compared the proposed approaches for the LRPH on four set of benchmarking instances adapted from the literature. The results show the effectiveness of GSA, imposing several best-known results within short computing times.