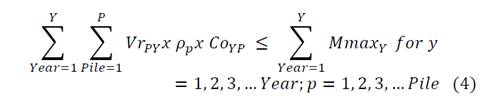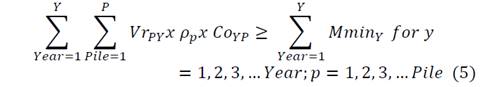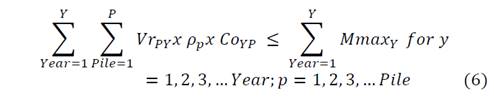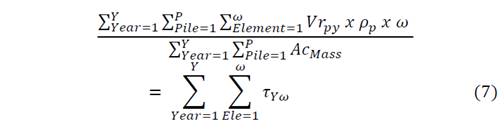1. Introduction
Usually, mine planning objectives are to develop a production scheduling that leads to an ore block selection that ensures the delivery of budget tones and grade quality to the processing plant according to the desired period [1]. There are minimum quality requirements for the ore delivered to the plant, and defining a mixture ratio and a technical control methodology is important to reach this quality target [20] [17]. The ideal operation should provide a uniform feed, since grade and tonnage variations are related to a trend in increasing operational costs [12]. The classic proposition, developed by Johnson [8], to calculate the net present value implies that costs affect the adequate time period to process a mining unit, and processing and rehandling costs will vary depending on mineralogy and ore type. Traditionally, blending algorithms only target quality and tonnage goals to provide results.
In most cases, the blending objective is the same: to ensure constant feed volume and ore quality in order to guarantee low operational costs. Each operation applies different techniques, but the main objectives are similar. The formulation of the blending scheduling problem through the classical linear approach is limited, since the objective function has only one goal. Linear programing presents difficulties on converging results with an increasing amount of constraints and variables [6]. An important characteristic of goal programing used in this formulation is related to deviations of the objective function, which is allowed but requires assigning a penalty to it. Loosening the objective function may lead to a non-optimal result, but the best possible result considering the modeled constraints [11].
The Direct Stockpile Scheduling is a mathematical formulation able to consider quality and mass constraints from the processing plant, and also the time impact required by mine planning related to costs and to proper discount factors. The relaxation of the objective function considers a possibility of a non-optimum solution to schedule the best feasible solution.
2. Ore blending and mine production scheduling
Ore blending is the process responsible for combining ore with various grades and contaminants in a systematic process. The importance of this process is directly related to the natural lithotype variability of the deposit [13]. Blending must combine different materials along time to reach an ideal product, uniform and homogeneous. The blending activity shows even more importance in cases of inhomogeneous ore deposits and rigorous quality control of the commodity [2]. Production mine planning should consider plant design, environmental factors and market demand. A brief description of these important factors is provided below:
Processing plant design: The processing plant is planned and built considering specific ratios between elements and mineralogy. Blending must attempt to estipulate the minimum and maximum limits to be accepted by the processing plant during the whole mine life [2]. Under or over utilization of material may lead to product losses due to this specific range.
Environmental factors: In some cases, there may be limited areas to be used by the stockpiles due to environmental restrictions. Thus, the environmental restrictions, mine scheduling, stockpile scheduling and plant must be aligned.
Market demand: Market agreements are developed based on ore quality and quantity. In order to ensure the product quality, it is important to provide a uniform feed for the processing plant, and this requires combining all productive units scheduling [12].
There is a kind of gap between the planned stockpile for long and short terms. A long term pile is scheduled based on interpolations provided by block models with less detailed information when compared to a short term one. After being mined, generally piles are sampled and apply adequate estimation techniques to provide an increase of information confidence [16]. Due to this increasing knowledge, the short term stockpile planning is more effective and hence more acceptable than long term planning.
A qualified stockpile planning must satisfy material quality, mass and operational cost targets. The main aspects considered in short term planning are:
Predictability: The scheduling must consider the current plant constraints and others likely to occur in the subsequent periods. The planning must attempt to ensure ore quality, the targeted mass and costs.
Floatability: The scheduling of ore piles based on nonlinear programing may present fluctuations when the system can’t reach a desired target, due to strategies used to provide the nearest possible approximated solution [4]. If the deviations are foreseen during the mine planning, the plan may be analyzed in an attempt to overcome these fluctuations.
Regionalization: The block model must be the most accurate possible, since knowledge of the actual stockpile material and the run of mine are directly related to the quality of this information. Inaccurate block model estimation may lead to ore feed oscillations and thus turning unfeasible the use of stockpiles for quality control.
Stockpile control is an important tool to avoid selective mining, since blending different materials may maximize the reserve exploitation [18]. The stockpile control aims to minimize mining costs and increase ore production. Increase of ore reserves are expected as a natural consequence of stockpile blending: non-complying material with the quality standards, below the cutoff grade or with higher concentration of contaminants, which were initially considered as waste may be processed with material complying with the quality standards to blend and become acceptable to the processing plant [13].
3. Ideal stockpile formulation
One function of the mining complex is to supply ore blending to the plant according to the processing requirements. The first stage consists in mining the non-homogeneous material provided by the deposit. The second stage aims to blend different materials considering the processing plant requirements and finally process it [16]. For a given processing and operation path, it is possible to consider multiple alternatives. For example: a block can be mined and processed in the initial period or stocked to be blended later. Various processing routes may be chosen and all of them should result in material complying with the processing plant’s ore quality requirements [18].
The classical blending process considers the blend opportunity after deciding whether the block should be mined or not [10]. Ideally, this decision of whether the block will be mined or not should take the blending opportunity into account, for example: A high grade block with undesirable contaminant rates is likely to not be mined, however, if the system is able to consider the blending opportunities, it can find an ideal proportion to maximize the utilization of this marginal block [12].
4. Goal programing
Goal programming, as linear programming, is a mathematical linear model but with several differences. Linear programming aims to solve problems modelled by linear one-dimensional equation. Profit maximization and cost minimization problem may sometimes be solved by linear programming. Real mine operations commonly require multiple objectives to reach an operational solution. Joining different objectives on a single objective function may be impossible. Goal programming solve this demand by allowing problem models constituted by multiples objectives [9].
Linear programming techniques regularly consider the constrains as inviolable, named hard constraints. Goal programing face this modelling limitation differently, at least one constraint is transgressed to reach a possible solution [7]. The constrains are named soft constrains.
Mining operations formulation commonly are correctly formulated on decision model by goal programming on a huge amount of problems. This operation is maximized or minimized by a group of constraints incompatible between equations [5]. The algorithm must be able to choose the constrain to be violated in order to reach a feasible solution.
Goal programming can be divided on the following components: Decision variables (real variables optimized by model), constraints (group of linear restrictions of objective functions), deviation variables (positive or negative deviation related of objective function) and objective function (mathematical relationship of decision variables representing the objective of model) [15].
5. Process description
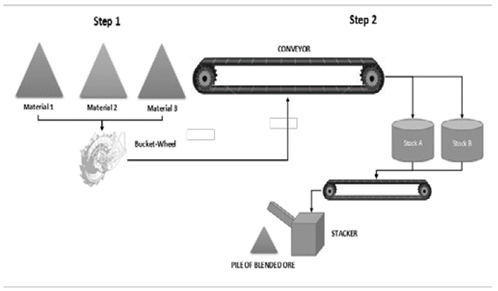
Generally the ore blending process is executed in 2 steps. First, different stockpiles are disposed in the field according specific proprieties. In this initial stage, the different stockpiles must be homogenized and sampled to determine their proprieties [20]. This step is important to split the different lithotypes and determine proprieties. Second, a bucket-wheel excavator and transport conveyor direct the different materials to temporary silos. The silos store the materials for the ensuing blending operations. The silos feed a transportation system to supply a stacker, by which the blended ores are stacked on the blending yard for the subsequent process [18]. Each silo discharges the ore at a specific flow speed according to the blending ratio determined to reach the aimed proprieties. The process occurs simultaneously, the two steps working at same time [2]. The process starts the ore preparation during stage 1 by bucket-wheel and finishes at the stacker. The silos allow the creation of a kind of intermediate buffer of pile blending ore, due to operational restrictions such as weather, for example, that can interrupt the process. Operational problems on main equipment can still stop the process. If any silo runs out of ore and the bucket-wheel can’t move to a certain pile on time to excavate or to refill it, the whole process has to pause [2,9]. Fig. 1 shows an example of blending process to build the ore stockpiles.
6. Formulation of direct pile scheduling
The classic strategy to solve blending problems is based on linear programing, due to the facility of its implementation and formulation building. A classical formulation is able to mix a number of components according to a specific requirement group. There are several variations of the blending problem formulation using linear programing as reported by [1]. Since [4] published in 1963 one of the main books on linear programing, several formulations have been raised to solve these formulations. Johnson [8] published a formulation to solve the scheduling problem based on linear programing, but due to computational restrictions, this methodology was abandoned during the 90’s. Nowadays these formulations are refined using a relaxing mechanism and heuristic techniques.
In some cases, the ore pile does not have sufficient material to fulfill a specific requirement. Then, a technique must be used that is able to determine the best scenario possible with the present material [20]. Goal programing is not a new technique, but a formulation considering minimization of the operational costs, quality requirements, correct discount factor and opportunity cost in the same formulation can be an interesting alternative.
-
Objective Function: Goal programing is a kind of multi objective optimization which permits a multi-criteria goal decision. Applied in formulations with needs to attempt and satisfy more than one objective function [8] [19]. The present formulation must attempt a minimal operational cost eq. (1) and minimum quality deviation eq. (2).
Vr YP = Material volume recovered of especific year(y) related to each feed pile(p);
𝜌 𝑃 = Feed pile density;
𝑂𝑐 𝑌𝑃 = Operational cost of especific year(y) related to each feed pile(p);
??𝑜 𝑌𝑃 = Oportunity cost analysis factor represented by a binary variable;
𝐷𝑓 𝑃 = Economic discount factor for each period(p);
𝛿𝑙 − = Lower negative deviation for volume;
𝛿𝑙 + = Lower positive deviation for volume;
𝛿𝑢 − = Upper negative deviation for volume;
𝛿𝑢 + = Upper positive deviation for volume;
-
Maximum Permitted Distance: To obtain an operational result, it is important to consider the distance between the feed piles. This distances are function of equipment and field size. This control is based on linear restriction as proposed by Romero [15]. Control distance is an alternative to blend closer material and ensure efficiency of operational activity.
𝐷 𝑌𝑃 = Distance between the piles of the year;
NP = Number of piles used of the period;
𝑃𝐷 𝑦 = Maximum distance permitted in the period(y);
-
Operational and Quality restrictions: Operational restrictions are related to operational plant restrictions. There are upper and lower boundary restrictions to control the capacity. Each period can present different restrictions according to the mine planning.
Mmin 𝒀 = Minimum mass in year;
𝑴𝒎𝒂𝒙 𝒀 = Maximum mass in year;
Mass must be limited by upper limit manly due a difficulty in keeping a huge, uniform pile; the lower limit is related to operational cost [11].There is an opportunity cost analyzed by the 𝐶𝑜 𝑌𝑃 binary variable. This variable permits the algorithm to determine if recovery of the pile is important to reach the quality and minimize the costs [20]. The algorithm can decide not to recover the pile due to blend options for obtaining the objectives.
7. Method
To implement the theory described in items 3, 4, 5 and 6 was used the concepts of "Goal programing" applied the Python language. Was developed an algorithm based on linear optimization able to access Optimization Gurobi tools to solve the problem. The algorithm is able to access a database that represents a block model to determine the best mixture of ores in order to reach the demand of the plant. First the algorithm was tested on experimental database. After math and technical validation of the results was implemented in a real project. The operation has 10 waste supplies that should be adjusted to feed the plant. Operational constraints and characteristics of the processing plant was supplied to set the algorithm constrains. The results of this test are presented in the following items.
8. Tests and results
The proposed formulation must be tested on a real system to verify the target attempt ability of the algorithm. The database used corresponds to an iron ore deposit formed on Pre-Cambrian inside the "Quadrilátero Ferrífero". This formation is a typical amount of the greenstone belt, formed by Meta volcanic rocks and Meta sediment [3].
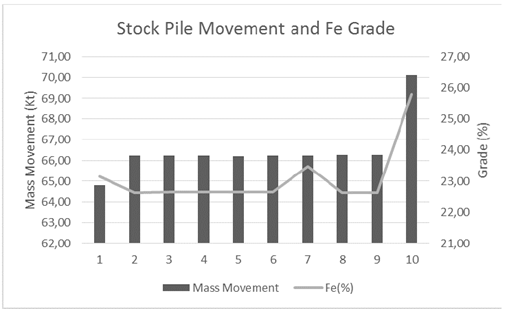
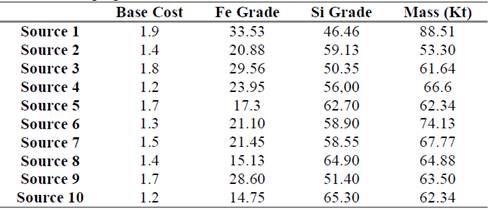
Cost was composed by base cost and an increment cost, due to a distance between the sources feeds. Figure 2 shows the proprieties of source with will compound the desired solution and targets shown in Table 1.
The movement of mass attempting to fulfill the restrictions is a problem of hard convergence as expected, due to a double objective function and the input restrictions. The solution strategy does not forbid a result for the objectives, due to the formulation construction applying a penalty in order to converge to desired solution, if it cannot converge exactly [6].
Table 1 shows the quality of all ore sources, there are 6 sources with quality below the plant feed requirements. According to plant restrictions these 6 sources cannot feed the process. It is possible to observe the results of stockpile optimization on Figure 2 and Figure 3. All the ore with quality below the limits was adjusted, because the overall quality in all years is greater than 22.5% Fe and smaller than 57.35% of Si. The resource was increased due to the ability to choose the restriction to be violated [9]. The ore movement restriction is out of parameter, less than 66.20 Kt on the first year one and greater than 66.20 Kt on year 12.
Initial reserves able to feed the plant was 280.25 Kt, and after goal programing optimization it increased to 665.01 Kt. This represents an increase of 237 percent of material that initially was conducted to waste dump. After the optimization the mine cut-off was decreased turning a huge amount of material profitable.
9. Conclusion
Blending is an important issue in mine planning because the quality is important to produce adequate products. Correct targets related to quality and mass can make a project to become feasible. Adequate use of information about the stock is important to keep the plant working as planned and increase the feasible reserve. The proposed formulation aims to use the feed piles to create stockpiles to be used on plant considering the targets and restrictions. The results point to violate the mass restriction because respecting the grade constraint ensures the possibility of processing this material. Material below quality requirements is taken as waste, which is a huge impact. Violating stockpile grade means the material cannot be processed, and violating the production mass constrain reflects on an opportunity cost problem related to profit. Therefore, the production mass target problem doesn’t affect the reserve, and it is better to keep the grade restrictions rather than the production mass ones.
The small amount of ore on the first year is related to cost, the formulation set an objective to minimize the operational costs. On initial years the best alternative is to use the low cost and lower quality stock piles, but respecting the ore quality. Results show ability to create a feasible blending scenario when the targets cannot be reached exactly. Relaxing the problem allows the system to obtain a feasible solution to the problem. According Rendu [14] the lack or surplus of ore mass can generate an opportunity cost. A lack of ore causes equipment otiosity, a surplus of material can force the system to process the low grade ore fist. Process low grade ore first causes a an income decrease for the company. The linear programing largely used cannot find a scenario from the objective constraints. The present scenario reached the targets for a majority of the periods, demonstrating a feasible result with low cost. The algorithm was able to determine a viable solution in a difficult solution. In the future you can apply heuristic mechanisms, in order to incorporate more operational restrictions.