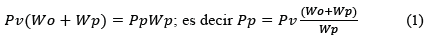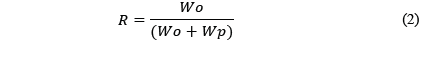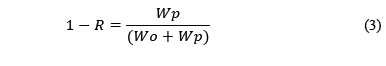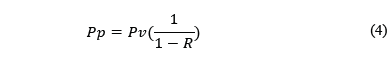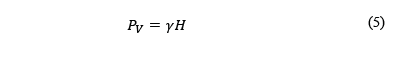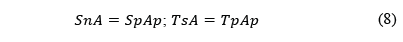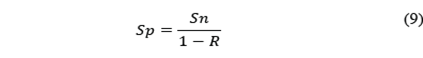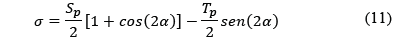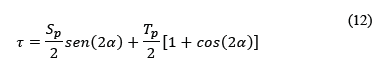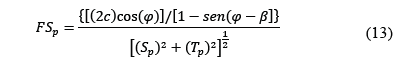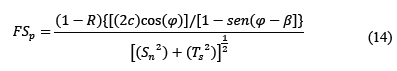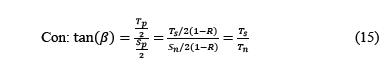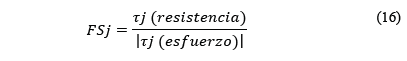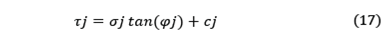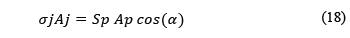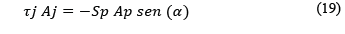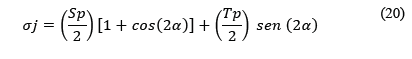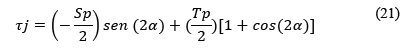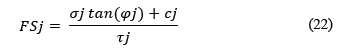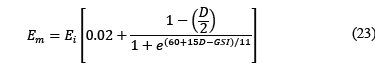1. Aspectos sobre el diseño de pilares en minería
Los métodos de explotación que involucran cámaras y pilares se basan en lograr que los campos de desplazamientos inducidos por las excavaciones tanto en el campo cercano como lejano, estén restringidos a órdenes de magnitud elásticos. La energía elástica de deformación se almacena en forma de concentración de tensiones en los pilares y en el macizo rocoso que conforma el campo cercano. El objetivo es asegurar que no se produzca un aumento repentino de la tensión sobre los pilares.
Geológicamente las vetas auríferas en Colombia se caracterizan por el emplazamiento de filones hidrotermales en intrusiones de plutones dioríticos o graníticos. Este tipo de yacimientos son emblemáticos por su importancia histórica y económica; según [1], algunos de este tipo son los de Segovia, Remedios, Zaragoza, El Bagre (Antioquia), Serranía de San Lucas (Bolívar), Marmato (Caldas), Santacruz y La Llanada (Nariño), en los cuales se desarrolla pequeña y mediana minería caracterizada por la aplicación de variaciones del método de explotación de cámaras y pilares, en los cuales los pilares de rocas son estructuras portantes fundamentales.
1.1. Definición de pilar minero
En [2] Coates define un pilar como "…la roca in situ situada entre dos o más excavaciones subterráneas"; sin embargo, una definición funcional puede ser de mayor claridad, pues un pilar es un elemento estructural natural, temporal o permanente, compuesto por mena o roca estéril, encargado de recibir y soportar las presiones del terreno con el fin de evitar el colapso de las excavaciones.
1.2. Uso de pilares en minería de vetas auríferas angostas
Las motivaciones de uso de los pilares son variadas, así como su denominación. Los pilares aislados son estructuras remanentes después de procesos de explotación desde su perímetro, por lo cual definen unidades independientes. Los pilares de corona son usados para la protección de vías principales, conocidos coloquialmente en Colombia como “machones” o “pilares corridos” (chain pillar); son estructuras con la dimensión en el rumbo de la veta mucho mayor que las otras dos dimensiones, se establecen con el fin de definir y proteger vías de preparación excavadas en las vetas de valor. Comúnmente estos pilares permanecen con sus dimensiones iniciales durante el tiempo que estas vías sean necesarias, Este tipo de pilares están en condición de carga biaxial debido a la roca circundante.
Los pilares barrera son estructuras con la función de disminuir la transferencia de cargas de forma a proteger las vías principales o la infraestructura de importancia, delimitando paneles o bloques, estos pilares ayudan a que cada sector se desarrolle de forma independiente, están en condición de carga biaxial y su dimensión en la dirección del buzamiento de la veta es mayor que las otras dos dimensiones. Es de anotar que el núcleo de cualquier tipo de pilar puede considerarse en estado de confinamiento triaxial.
1.3. Métodos de diseño de pilares mineros
Los métodos de diseño de pilares más utilizados para trabajos subterráneos en minas pueden ser clasificados en analíticos, empíricos, geológicos, de observación y de cumplimiento [2].
Métodos analíticos: utilizan los análisis de esfuerzos y deformaciones alrededor de las aperturas; incluyen técnicas como las soluciones de forma cerrada y las simulaciones con métodos numéricos. Métodos empíricos: evalúan la estabilidad de las aperturas mineras por el uso de sistemas de clasificación ingenieriles del macizo rocoso, los cuales proporcionan predicciones simples y económicas de la seguridad de techos, hastiales y demás requerimientos de soportes; entre éstos, los métodos de clasificaciones de macizos rocosos más usados son NGI-Q y RMR. Métodos geológicos: básicamente buscan identificar las estructuras geológicas y otros rasgos que afectan la estabilidad. Métodos de observación: Se fundamentan en el monitoreo actual o retrospectivo del movimiento del subsuelo durante la excavación para detectar la inestabilidad que pueda ser medida, y en el de la interacción subsuelo-estructura de soporte; este método incluye el Método Austriaco de Túneles (NATM) y el método de Convergencia-Confinamiento. Métodos de cumplimiento: se fundamentan en cumplir con los requerimientos mineros de rentabilidad, ventilación, transporte, etc.
Adicionalmente, la experiencia minera en distintas áreas contribuye al desarrollo de técnicas de aplicación de base experimental que suelen cumplir los objetivos bases de estabilidad y seguridad [3,4]. Por otro lado, es importante poner de manifiesto que el éxito del diseño de una explotación por cámaras y pilares radica no sólo en el hecho de que los pilares sean estables, sino que se deberá a su vez comprobar que las cámaras mineras no presenten problemas de estabilidad de los techos [5].
2. Esfuerzos en pilares
La carga actuante sobre un pilar obedece en primer lugar al estado de esfuerzos presente en el subsuelo y en segundo lugar a la localización y dimensiones del mismo pilar, por lo tanto, las condiciones semejantes locales tanto de los esfuerzos como de sus efectos sobre las rocas pueden aportar información valiosa que pude ser obtenida con la observación, obviando en parte el difícil proceso de medición de esfuerzos.
El método tradicional de cuantificar la carga sobre el pilar es conocido como Teoría del Área Tributaria; sin embargo, métodos rigurosos de diseño deberían provenir de la medición de los esfuerzos in situ. Otros modelos de cuantificar las cargas, como la teoría del arco de presiones, la bóveda de carga de Terzaghi o modelos numéricos pueden ser aplicadas.
2.1. Teoría del área tributaria
Este método supone que el esfuerzo sobre el pilar es determinado por el peso de la columna de roca situada sobre dicho pilar, adicionado de la columna situada sobre las excavaciones de forma proporcional a sus tamaños. En la Fig. 1 se representa este concepto para pilares horizontales, donde Wp es la longitud del pilar, b es el ancho del pilar, Wo es el ancho de cámara, Pv es el esfuerzo vertical y Pp es el esfuerzo axial medio sobre el pilar.
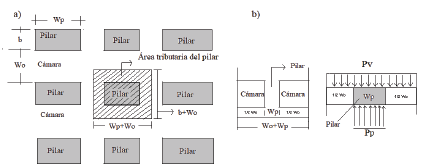
Fuente: [6].
Figura 1 Diagrama de cámaras y pilares con fuerzas en planta y en sección transversal unitaria: a) área tributaria del pilar b) fuerzas en pilar, en sección transversal al rumbo de la veta; las cargas sobre el pilar corresponden con el peso de la columna de roca del área tributaria que lo suprayace hasta superficie.
De acuerdo con la Fig. 1, el equilibrio bajo fuerzas internas conduce a la ecuación:
Por otro lado, si se expresa la razón de extracción (R) como la cantidad de mineral extraído con relación a la cantidad disponible, el aumento de la extracción aumentará el esfuerzo promedio en el pilar:
es decir
Reemplazando la ecuación (3) en la (1) se tiene que:
La ecuación (4) muestra que el máximo vaor que puede alcanzar R es 100%, en cuyo caso teóricamente el esfuerzo en el pilar, con dimensiones cero, tiende a infinito [6].
En el caso de pilares inclinados, el diagrama de fuerzas se representa en la Fig. 2, donde γ es el peso unitario de la roca, H es la profundidad de localización del pilar hasta superficie, k es la relación de esfuerzos in situ horizontal a vertical, β es la inclinación de la pared del pilar, Wp es el ancho del pilar y Wo es el ancho explotado.
Si se consideran sólo los esfuerzos litostáticos iniciales verticales
y
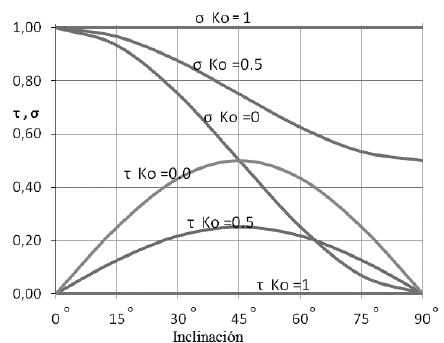
se tiene que tanto Ko como la magnitud de los esfuerzos producen modificación de las componentes normal o cortante según el ángulo de inclinación del pilar, esto se representa en la Fig. 3.
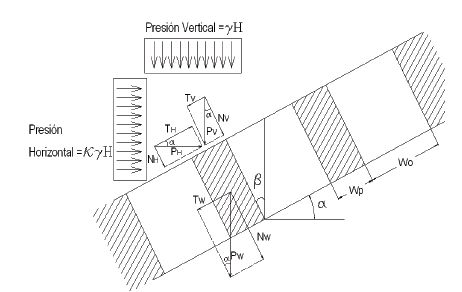
Fuente: Los Autores.
Figura 2 Diagrama de fuerzas sobre un pilar en una veta con inclinación α, se muestran: presión horizontal PH y presión vertical PV, sus componentes normales NH, NV y tangenciales TH y TV. El pilar tiene un peso PW y sus componentes son NW y TW.
Fuente: Modificado de [6].
Figura 3 Variación de los esfuerzos normales y cortantes normalizados sobre el pilar según el ángulo de inclinación y la relación de esfuerzo horizontal a vertical ko. Las componentes normales disminuyen con la inclinación, pero las componentes cortantes aumentan hasta un máximo en 45°.
El análisis anterior se ha hecho sin considerar los esfuerzos debidos al peso del pilar; esto tiene importancia pues, como se observa en la Fig. 3, para inclinaciones mayores de 45° la componente cortante del esfuerzo empieza a disminuir, pero el peso del pilar genera esfuerzos cortantes que pueden conducir a su deslizamiento, por lo cual deben ser considerados.
3. Resistencia de pilares bajo esfuerzos de compresión
Si considerada una definición de resistencia como la capacidad de carga última por unidad de área, el desempeño mecánico de los macizos rocosos con función portante está determinado inicialmente por sus dimensiones y por el campo de esfuerzos actuantes, el cual es modificado por las excavaciones y volúmenes cercanos. El campo de esfuerzos es caracterizado estáticamente por un tensor compuesto de magnitud, dirección y plano de acción, sin embargo, el conocimiento de este campo tampoco es suficiente para evaluar el desempeño mecánico de un pilar real, pues este es un elemento tridimensional natural que presenta estructuras que modifican la disposición interna de los esfuerzos, lo cual puede influenciar la estabilidad de manera definitiva.
De todas formas, es usual en el diseño de pilares utilizar el concepto de Factor de Seguridad (FS), que es el cociente entre la resistencia última del pilar y un determinado esfuerzo actuante. Según [7] la resistencia de los pilares depende de las dimensiones del pilar, de la relación ancho/altura del pilar (W/H) y del ancho de la cámara excavada. El objetivo del diseño consistirá entonces en determinar unas dimensiones que garanticen la integridad mecánica del pilar como elemento de soporte y maximicen la extracción del mineral de valor.
En [8] también se expone que la resistencia de los pilares depende de: a) el tamaño o efecto volumen del pilar, b) efecto de la geometría del pilar, y c) las propiedades del material del pilar. Sin embargo, es claro que el desempeño del pilar como elemento portante depende también de otros aspectos, para citar algunos: la resistencia mecánica y orientación de las discontinuidades existentes en el macizo que compone el pilar. El método de excavación, pues las voladuras afectan el macizo remanente en mayor grado que los métodos mecánicos o manuales. La interacción techo-pilar-piso, especialmente las diferencias de rigidez. La influencia de los procesos de debilitamiento de la roca, tales como alteraciones físico-químicas, y procesos esfuerzo-deformación dependiente del tiempo como el creep o fluencia y la relajación. La dinámica de los esfuerzos y otros factores más también afectan el desempeño.
Estos factores son de difícil inclusión en los modelos de diseño, por lo cual, para definir la resistencia de los pilares generalmente se acude a técnicas experimentales, numéricas y empíricas, entre las cuales:
Medidas en laboratorio de varios especímenes de rocas y extrapolación de propiedades a escalas reales, sin embargo, las mediciones de resistencia en probetas tienen deficiencias en representar la heterogeneidad, anisotropía y discontinuidad de los macizos rocosos.
Medición de esfuerzos, son realizadas muy pocas veces debido a sus costos y complejidad.
Retroanálisis por observación y monitoreo de pilares fallados, son factibles de realizar por personal entrenado y resultan viables en lo técnico y en lo económico.
Diseño por modelos numéricos en medios continuos o discontinuos, requieren de información representativa y confiable que debe ser obtenida en un proceso metódico y de cierto costo económico.
La bibliografía sobre el tema indica que las pruebas de laboratorio e investigaciones in-situ han sido realizadas con el objetivo de estimar la resistencia de pilares de minas produciendo formulaciones que se han centrado principalmente en describir el efecto sobre la resistencia de la forma, el tamaño y la esbeltez del pilar. Dos tipos de formulaciones han predominado históricamente, las ecuaciones empíricas tipo Salamon-Munro y las del tipo Obert-Duvall.
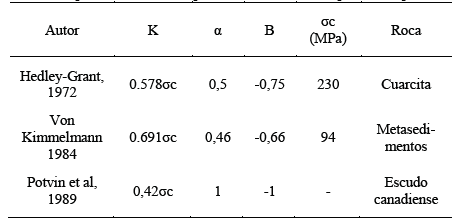
Las ecuaciones de tipo Salamon-Munro son de la forma:
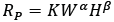 donde Rp es la resistencia del pilar, K, α, β son constantes empíricas, W es el ancho del pilar y H es la altura del pilar. En la Tabla 1 se presentan propuestas de este tipo, σc es la resistencia a la compresión uniaxial de la roca intacta.
donde Rp es la resistencia del pilar, K, α, β son constantes empíricas, W es el ancho del pilar y H es la altura del pilar. En la Tabla 1 se presentan propuestas de este tipo, σc es la resistencia a la compresión uniaxial de la roca intacta.
Las ecuaciones tipo Obert-Duvall son de la forma:
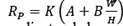 donde A y B son valores dependientes de la roca del pilar, W es el ancho del pilar, y H es la altura del pilar. En la Tabla 2 se presentan algunas propuestas de este tipo.
donde A y B son valores dependientes de la roca del pilar, W es el ancho del pilar, y H es la altura del pilar. En la Tabla 2 se presentan algunas propuestas de este tipo.
El Factor de Seguridad de un pilar bajo compresión es definido por el cociente entre la resistencia del pilar Rp y el esfuerzo medio que el pilar recibe Pp. La resistencia puede ser calculada desarrollando una fórmula propia para cada yacimiento o en su falta, usando alguna de las fórmulas anteriores.
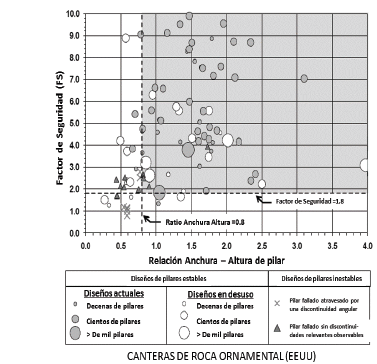
Una comprobación interesante basada en el hecho de que los pilares más proclives a fallar son los más esbeltos (bajo ratio anchura / altura) y en una amplia experiencia de explotaciones subterráneas en roca en Estados Unidos [10], es la comprobación de que dicha relación se encuentre por encima de 0.8, al mismo tiempo que el FS esté por encima de 1.8. Como muestra la Fig. 4, los pilares en roca así diseñados serán estables en la mayor parte de las situaciones.
Fuente: [10].
Figura 4 Diagrama de estabilidad basado en Factor de Seguridad y relación anchura/altura de los pilares, propuesto como resultado de seguimiento de una base de datos de pilares en roca en Estados Unidos.
A partir de la experiencia de los autores en Colombia y España [11], se recomienda utilizar para el diseño de nuevas explotaciones FS mayor a 2 para asegurar un cálculo conservador y económico de las reservas. Una vez la mina comience la explotación, se puede ajustar el FS a 1.75 o 1.8 de forma que se pueda aumentar algo la recuperación y observar si se produce algún tipo de inestabilidad incipiente. Si tras varios años de explotación utilizando el FS anterior, se constata que los pilares no han mostrado síntomas de inestabilidad, el FS puede bajarse hasta 1.6 o 1.5 para zonas nuevas [12]. No se recomienda bajar de este valor, pues dada la naturaleza heterogénea de los macizos rocosos que forman los pilares, para diseño de mayor riesgo será relativamente común que algún pilar sea inestable.
4. Metodología propuesta para el diseño de pilares
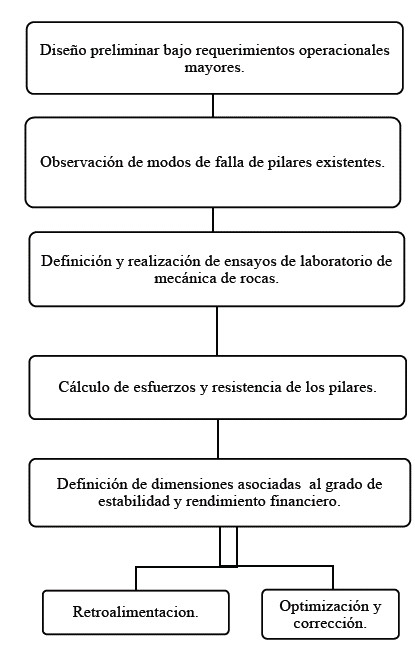
Con base en lo observado en la pequeña y mediana minería subterránea de vetas en algunos casos de Colombia, se proponen las etapas de diseño de pilares presentadas en la Fig. 5.
5. Observación de modos de falla de pilares existentes
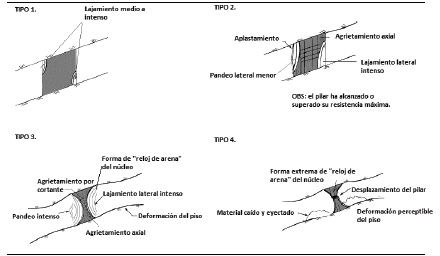
Aspecto fundamental en el dimensionamiento de pilares es la capacidad de utilizar la experiencia de forma metódica y aplicada al caso específico de cada yacimiento mineral. Esto implica la necesidad de observar, analizar y sintetizar sobre el comportamiento mecánico del terreno desde un enfoque geotécnico, en el cual es necesario considerar el material de veta constituyente del pilar y de los respaldos como un macizo rocoso. En este sentido es útil la experiencia recopilada en [2] donde se expone que hay tres modos de falla de pilares en rocas duras como las que nos ocupan: 1) falla controlada por estructuras, 2) falla por esfuerzos inducidos progresivos y 3) explosión de pilares (pillar bursts). Estos modos de falla hacen parte de un proceso sucesivo que se esquematiza en la Fig. 6.
Fuente: Los autores con adaptación de [2].
Figura 6 Mecanismos y proceso de ruptura de pilares en rocas duras.
Los mecanismos citados provienen de ambientes geológicos diferentes, por lo cual es necesario constatar si son verificados en cada yacimiento. Para respaldos de rigidez y resistencia elevadas tales como las rocas graníticas o dioríticas en las vetas colombianas, la descripción del modo de falla se debe centrar en la veta que constituye los pilares en mayor medida debido a su menor resistencia y en segundo lugar en la roca de respaldos inmediatos, pues ocasionalmente también conforma pilares.
Se deben observar las variaciones composicionales y de orientación espacial de las vetas en explotación y de las estructuras asociadas que constituyan planos débiles, tales como cizallas, salbanda, contactos litológicos, fracturas, diaclasas, etc con la intención de dimensionar la variación de sus propiedades en diferentes puntos de las labores mineras. Se deben medir, potencias, espaciados, persistencias, rugosidad, rellenos y en general composición, dimensiones y orientación espacial de las estructuras. Con esta finalidad se pueden seguir las guías presentadas por ejemplo en [13].
Con este fin son muy útiles los pilares aislados debido a que es posible ver las evidencias en tres dimensiones, para así identificar el mecanismo de ruptura. Generalmente la identificación de los planos débiles conduce a centrar la atención en la roca cizallada, fracturas y salbanda contenidas en la estructura vetiforme principal y en los respaldos de techo y piso.
A modo de ilustración de la observación de los modos de falla se presentan vetas situadas en el Batolito de Segovia, donde las mineralizaciones están formadas por filones auríferos de cuarzo con sulfuros de plomo, zinc, cobre y hierro. Oro y plata se encuentran libres y diseminados en los sulfuros. La roca de respaldos consiste de rocas dioríticas y gabros. La observación condujo a resaltar la importancia de las discontinuidades paralelas y contenidas en las vetas que se indica en las fotografías siguientes, produciendo modo de falla de pilares claramente de causa estructural. Los silicatos y sulfuros son proclives a la alteración y por lo tanto también debilitan mecánicamente los pilares, especialmente en ambientes de alta humedad.
En las fotografías siguientes se ilustran algunos mecanismos en pilares aislados y de corona, Figs. 7-13.

Fuente: Fotografía tomada por Álvaro Castro.
Figura 7 Detalle de veta mineralizada con sus estructuras y respaldos inmediatos, Batolito de Segovia, Antioquia
Teniendo en vista los modos de falla y procesos ilustrados, la metodología de diseño propuesta se fundamenta en la descripción de los pilares ya existente con el fin de identificar los mecanismos de ruptura evidentes. En las zonas explotadas se observan los pilares antiguos, buscando y describiendo evidencias sobre el tipo de deterioro y falla que permitirán definir el modelo de ruptura.
En los pilares debe prestarse atención a las fracturas “artificiales” producidas por las voladuras, pues también ocasionan inestabilidad.

Fuente: Fotografía tomada por Álvaro Castro.
Figura 8 Pilar mostrando falla por esfuerzos inducidos progresivos originando lajamiento lateral o spalling, Batolito de Segovia, Antioquia.

Fuente: Alvaro Castro.
Figura 9 Pilar mostrando falla por control estructural, grietas axiales por esfuerzo cortante, desplazamiento de bloques, eyección y meteorización. Batolito de Segovia, Antioquia.

Fuente: Fotografía tomada por Álvaro Castro.
Figura 10 Veta inclinada, pilar que se encuentra bajo esfuerzos de compresión y de corte. Se marcan las estructuras débiles naturales preexistentes que pueden inducir deslizamientodebido al desconfinamiento y a superación de laresistencia al cortante de las discontinuidades. En la estructura del pilar no se evidencian fracturas verticales o diagonales que pudieran indicar falla por compresión o por cortante a través del cuerpo de roca. El grado de oxidación de los minerales es incipiente. La posibilidad de reemplazo de pilarescon otros materiales es una opción por evaluar. El Bagre, Antioquia.

Fuente: Fotografía tomada por Álvaro Castro.
Figura 11 Pilar que muestra fracturas axiales y laterales inclusive en el núcleo del pilar (deterioromecánico) y oxidación (deterioro químico), la inestabilidad se observa continuar a través de las fracturas paralelas, en rumbo y buzamiento, a la veta cuarzosa principal. El proceso se manifiesta en desprendimientos de bloques e indicios de spalling o lajamiento a media altura, proceso que es típico de un estado medio o avanzado de falla. El Bagre, Antioquia.

Fuente: Fotografía tomada por Álvaro Castro
Figura 12. Vía de preparación por el buzamiento de la veta tipo “tambor”. Los macizos de veta, piso y techo son de buena calidad, los contactos son cerrados lo cual se manifiesta en estabilidad aún en inclinaciones de veta casi verticales. Se marcan las estructuras que eventualmente pudieran definir la inestabilidad en un proceso de deterioro futuro, especialmente por efecto del agua y desconfinamiento de base; un método de explotación de corte y relleno ascendente puede manejar esta situación de forma satisfactoria. El Bagre, Antioquia.

Fuente: Fotografía tomada por Álvaro Castro
Figura 13 Salbanda en la base del pilar; dependiendo del tipo y espesor de este material blando, puede ser importante para la estabilidad, siendo necesaria su caracterización de resistencia y deformación según los métodode la mecánica de suelos. El Bagre, Antioquia.
6. Cálculo de pilares por resistencia al corte de discontinuidades
Los pilares en estructuras inclinadas como vetas están sometidos a esfuerzos de compresión y cortante, por lo que se requiere un criterio de ruptura que considere los dos procesos. El criterio Mohr-Coulomb sirve para este fin, pero el uso de esfuerzos medios conduce a una representación no-convencional del círculo de Mohr que puede ser generalizado para el caso donde los esfuerzos de corte actúan sobre los planos inferior y superior del pilar, pero no sobre las paredes laterales. Este círculo de Mohr no está centrado en el eje de esfuerzos normales. Esta situación no ocurre en capas horizontales donde el esfuerzo cortante no existe, ver la Fig. 3.
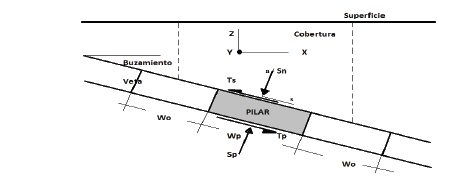
Si se considera que la base del prisma del pilar está inclinada, los esfuerzos antes de la excavación en la base y techo del pilar son en compresión perpendicular al buzamiento y tangenciales paralelos al buzamiento, para el cálculo se considera el esquema de fuerzas de la Fig. 14.
En una aproximación, se puede considerar que las fuerzas gravitacionales de un bloque que suprayace el pilar antes de la excavación son las mismas fuerzas después de la explotación, por lo tanto:
Fuente: Modificado de [14].
Figura 14 Esfuerzos en un pilar en veta con buzamiento, Sn, Sp, Ts, Tp, A, Ap, son respectivamente el esfuerzo normal antes de explotación, esfuerzo medio después de explotación, esfuerzo cortante antes del minado, esfuerzo cortante medio después del minado, área tributaria y área del pilar. Estos esfuerzos actúan en la base y parte superior del pilar.
Las fórmulas del factor de extracción R son:
Como Sp y Tp son esfuerzos medios actuando sobre un área finita Ap, ellos no siguen las ecuaciones usuales de transformación de esfuerzos bajo rotación de los ejes de referencia, esto debido a que no existen esfuerzos de corte en los lados del pilar. Deben ser satisfechos equilibrios de fuerzas y momentos, y los esfuerzos normales se compensan. Si no hay esfuerzos cortantes no se requiere la compensación, el vuelco del pilar no es una preocupación. Los esfuerzos actúan en el techo y piso del pilar, éstas son por tanto superficies de tracción.
Los esfuerzos medios que actúan sobre superficies de un cuerpo de tamaño finito (no son esfuerzos en un punto) son:
α es el ángulo entre la dirección de Sp y la normal a la superficie inclinada considerada. De acuerdo con [14] el factor de seguridad por cortante según el criterio de Mohr-Coulomb es:
6.1. Cálculo de pilares con discontinuidades
Las propiedades de resistencia y deformación del macizo están influenciadas por las propiedades tanto de la roca intacta como de las discontinuidades existentes. Sin embargo, si se diera el proceso de ruptura del pilar, este debe incluir las estructuras débiles con preponderancia sobra la roca sana. Es necesario entonces observar la estructura de veta y los contactos con los respaldos. Lo analizado sobre los mecanismos de ruptura evidentes en los pilares existentes permite plantear un modelo de ruptura por cortante a través de las discontinuidades contenidas en la veta.
Las estructuras débiles que producen inestabilidad son las fracturas abiertas naturalmente o por las voladuras, las zonas de venas con rellenos minerales blandos y las capas de salbanda, principalmente. En algunos casos se presentan franjas de roca cizallada. Algunas veces las discontinuidades geológicas fallan, pero no el pilar como un todo, esto puede suceder con diaclasas, planos de contacto y otras estructuras frágiles o débiles.
Para el diseño de pilar necesitan ser examinados los mecanismos de falla por las diaclasas y por el pilar. Un factor de seguridad adecuado para discontinuidades debe incluir la resistencia al corte de la discontinuidad y el esfuerzo actuante sobre ella:
Con Mohr-Coulomb, la resistencia al cortante es dada por:
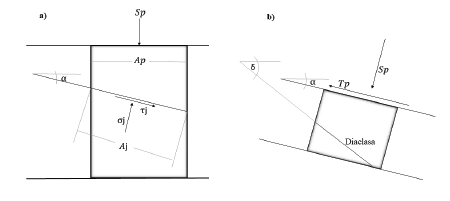
Donde el sufijo j se refiere a las discontinuidades, con propiedades consideradas conocidas. Se necesita un nuevo análisis para determinar los esfuerzos actuantes en la discontinuidad. En la Fig. 15 se muestra un esquema de la situación.
Con base en la Fig. 15 se pueden plantear las ecuaciones de equilibrio:
El signo negativo se refiere a la dirección señalada en la figura. El valor absoluto es usado en el cálculo del factor de seguridad. En el caso de que las estructuras tipo cizalla y diaclasas se orienten en la misma dirección, se requiere:
Una vez que los esfuerzos son obtenidos, se puede calcular el Factor de Seguridad:
Fuente
Figura 15 a) Pilar con una fractura en veta horizontal. b) Esquema de veta y fracturas buzando en la misma dirección
Fuente: Álvaro Castro.
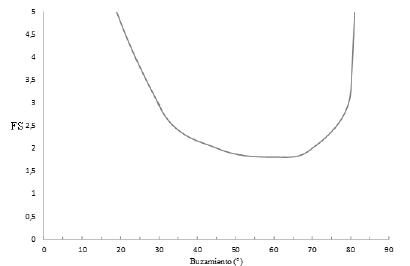
Figura 16 Efecto del buzamiento de una veta en el FS de pilar conformado por veta cuarzosa en una mina en El Bagre, Antioquia.
Este método de cálculo exige definir los esfuerzos antes y después de la excavación de explotación, así como las propiedades resistentes de las discontinuidades.
El diseño de pilares en minas subterráneas está tradicionalmente evaluado de forma determinista basado en el Factor de Seguridad (FS), en que se pueden definir tres condiciones:
FS>1, el pilar es estable.
FS=1, el pilar está en condición de equilibrio límite.
FS<1, el pilar está en condición de ruptura.
Si se determinan los esfuerzos por la teoría del área tributaria es posible llegarse a resultados de interés práctico, pero para el dimensionamiento de pilares en un dado caso es conveniente programar los cálculos de forma que sea posible observar la influencia de los parámetros en un determinado sitio de la explotación, en la Fig. 16 se ilustra por ejemplo el efecto del buzamiento.
7. Caracterización en laboratorio de mecánica de rocas
La caracterización básica necesaria es de esfuerzo-deformación y resistencia a la compresión uniaxial, estos ensayos permiten verificar además la rigidez de la roca que conforma tanto el pilar como los respaldos, así como su grado de fragilidad. Mejor aún es realizar ensayos de compresión triaxial en diferentes condiciones de confinamiento y la curva completa post ruptura de la roca, lo cual permitirá caracterizar la deformación y resistencia de la matriz rocosa bajo diferentes condiciones de carga.
De acuerdo con lo expuesto, los estudios de mecánica de rocas son dirigidos sobre los materiales controladores de la estabilidad de los pilares, es decir en el caso de rocas frágiles y resistentes que contienen discontinuidades es necesario conocer los parámetros de cohesión y ángulo de fricción de las discontinuidades. A este respecto se debe considerar el trabajo presentado en [15] quienes concluyeron que la rotura se inicia como formación de lajas o cáscaras (spalling, slabing) ocasionando pérdida de cohesión, lo cual se combina con resistencia friccional limitada debido a las bajas condiciones de confinamiento para su movilización, todo lo cual ocasiona deslizamiento en las estructuras de falla.

Fuente: Fotografía tomada por Álvaro Castro.
Figura 17 Aspecto de plano de falla en el ensayo de corte directo sobre discontinuidades en veta.
Con el fin de encontrar la cohesión y ángulo de fricción necesarios para el diseño, el procedimiento estándar es el ensayo de resistencia al corte por discontinuidades, (ASTM 5607, ISRM). En estos ensayos se obtienen las relaciones entre esfuerzo cortante versus desplazamiento cortante, de esfuerzo cortante residual versus desplazamiento cortante, y de resistencia cortante máxima versus esfuerzo normal. Series de estos ensayos permitirán obtener la cohesión y el ángulo de fricción del material de las discontinuidades. En la Fig. 17 se presenta un aspecto de este ensayo.
En la Tabla 3 se resumen los resultados de laboratorio de corte directo por discontinuidades y de carga puntual en muestras irregulares de rocas. Ensayos de carga puntual o de martillo Schmidt en cantidad adecuada pueden mejorar la caracterización por resistencia a la compresión de las rocas y discontinuidades.
8. Diseño de pilares por métodos numéricos
En ingeniería de rocas los métodos más comunes para modelar macizos rocosos son los de medio continuo y los de medio discontinuo. Software para medios discontinuos, como los de elementos discretos (DEM), pueden ser utilizados para el diseño de pilares, sin embargo, pocas experiencias se han informado sobre este tema y es escasa en el medio nacional la existencia de este tipo de simulador disponible para el mercado minero. De otro lado, es accesible el software para medio continuo, por lo cual se presentará aquí la experiencia con métodos de elementos finitos (FEM), que sin embargo requiere asumir el macizo rocoso (discontinuo) como un medio continuo equivalente isotrópico, por lo cual los resultados del modelo deben ser tratados con limitaciones.
Una vez obtenidos los resultados de los levantamientos directos y de las pruebas de laboratorio expuestos en las secciones anteriores, será entonces usada esta información para realizar geometrías y condiciones de prueba en el simulador. Por su importancia para el modelo numérico, el módulo de deformación del macizo rocosos que compone el pilar es un aspecto crítico. Diversas propuestas que pueden ser usadas existen en la bibliografía, para lo cual se recomiendan referencias como la [16].
El módulo de deformación del pilar y de la roca de respaldos es posible calcularse con la propuesta en [17]:
Donde Ei es el módulo de deformación de la roca intacta, GSI es el parámetro de la clasificación de Hoek-Brown y D es el parámetro de perturbación por voladuras.
Adicionalmente, es relevante considerar que, como se ha observado in-situ e implementado en las formulas empíricas presentadas, la resistencia del pilar depende de su tamaño y esbeltez. Por tanto, para caracterizar adecuadamente los parámetros resistentes de los pilares que se implementan en modelos numéricos se deben calibrar para el tamaño y esbeltez específica de los mismos, procedimiento descrito por ejemplo en [11,12]. En la Tabla 4 se relacionan los datos de entrada para un diseño por método de elementos finitos, así como algunos valores obtenidos de casos colombianos.
Tabla 4 Propiedades de los materiales obtenidos de ensayos de laboratorio y de levantamientos en el sitio.
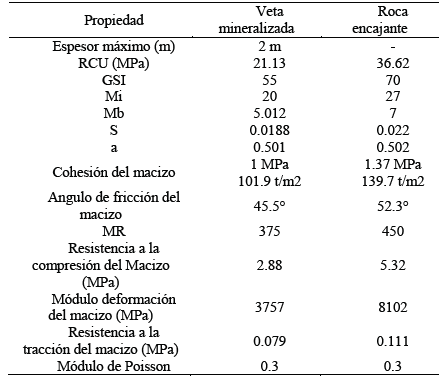
Fuente: Los Autores.
Es posible utilizar el criterio de ruptura Hoek-Brown, para lo cual es necesario realizar los levantamientos y los ensayos de resistencia a la compresión triaxial; este criterio es recomendado cuando el macizo rocoso que compone el pilar sea homogéneo, pues no considera el control estructural, muy común en vetas como se ha dicho.
Otra opción puede ser el uso de los criterios de resistencia cortante de discontinuidades tales como los de Patton, Ladanyi y Archambault o Barton-Bandis.
Los esfuerzos iniciales se pueden aproximar como litostáticos, para lo cual es necesario conocer la localización del pilar en el perfil estratigráfico. Una vez disponibles estos parámetros, se procede a construir el modelo numérico geométrico. En el ejemplo, todos los materiales se modelaron como elástico-frágiles debido a ser conocido su comportamiento en laboratorio y las evidencias de campo. El análisis de los modelos se concentra en el factor de resistencia (strength factor), esfuerzo principal mayor, esfuerzo desviador, desplazamientos totales máximos y deformación cortante máxima. En la Fig. 18 se presentan desplazamientos totales obtenidos con el programa RS2®.
9. Conclusiones y recomendaciones
Es necesario que las personas encargadas de las explotaciones mineras desarrollen métodos de diseño de pilares propios de cada yacimiento y sus condiciones, para lo cual es fundamental registrar las condiciones de falla de los pilares de forma a establecer mecanismos, formulaciones de resistencia, correlaciones empíricas y modos de ruptura. Adicionalmente es conveniente para la optimización de reservas que los titulares mineros o explotadores realicen inversión financiera y tecnológica en geomecánica.