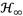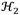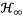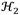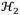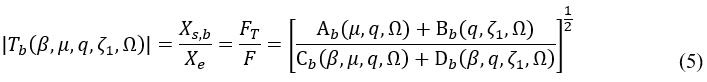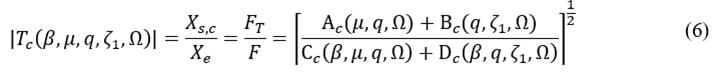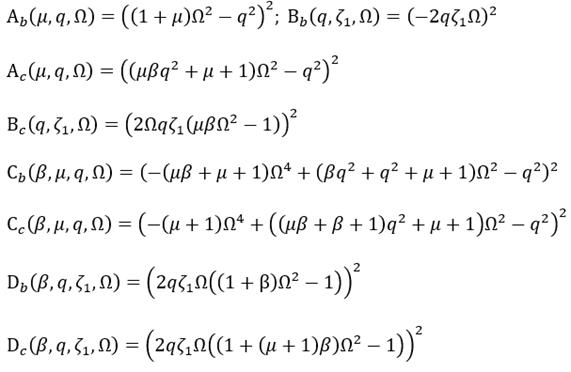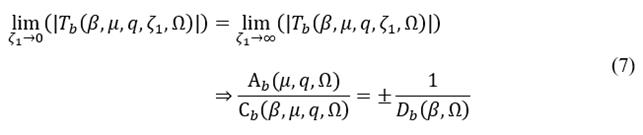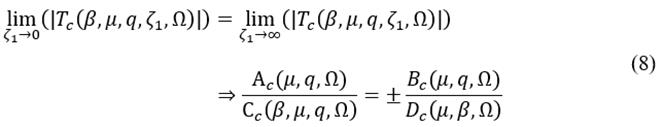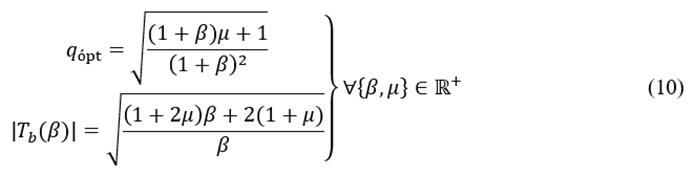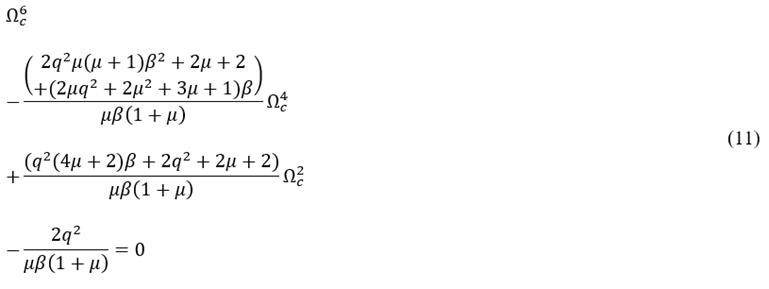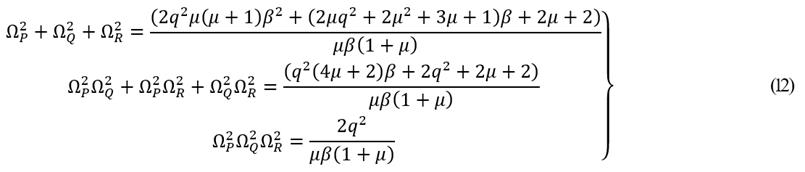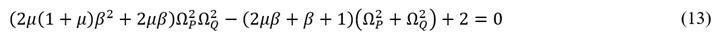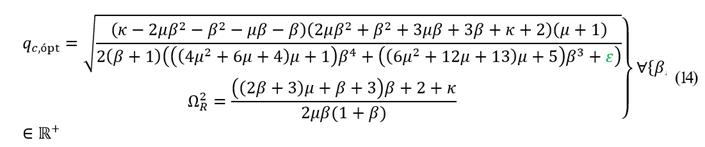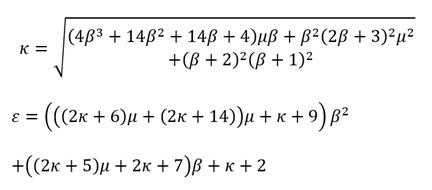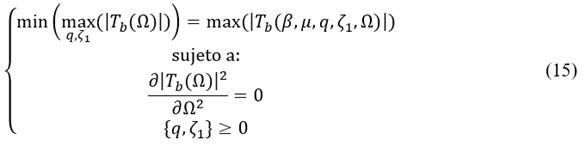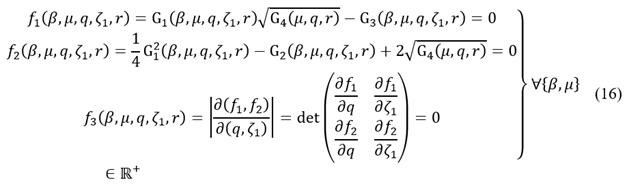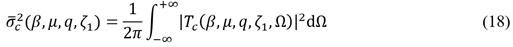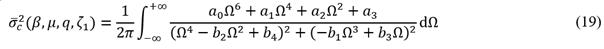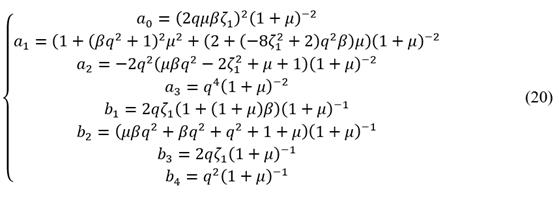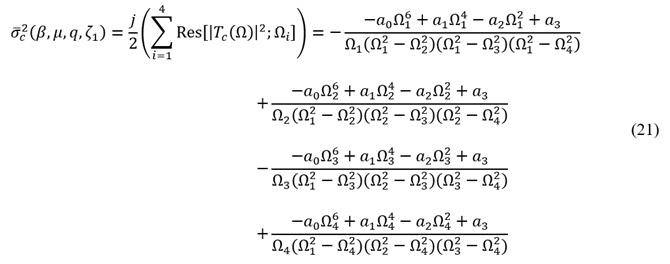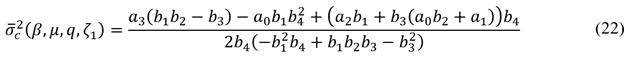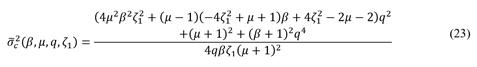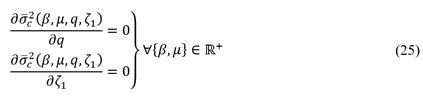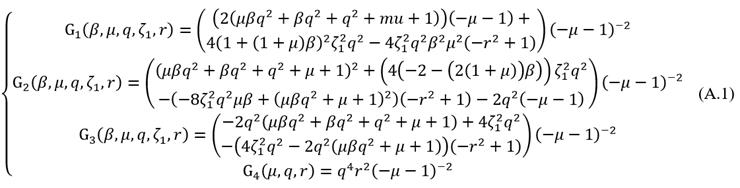Inglés (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Citado por Google 
Similares en
SciELO 
Similares en Google 
Permalink
1. Introduction
Vibration attenuation is one of the most important and challenging tasks into stationary and non-stationary mechanical structures subjected to the different kinds of environmental loads such as seismic excitation, wind loads, sea waves, vehicular traffic, among other excitation inputs. It is worth mentioning that most of these types of broadband power spectrum excitations are controlled via electronically controlled devices. However, active control techniques demand high power consumption, sophisticated control laws, bulky actuators, and so on. On the other hand, semi-active control can emulate the dynamic behavior of an actively controlled actuator while the threshold or saturation point of the device is not exceeded, demanding a minimal energy consumption. In contrast, passive control is one of the most widely used technologies in structural engineering due to its low implementation cost, it does not require industrial maintenance, and simplicity in the design topology, among other important characteristics. Dynamic vibration absorbers (DVAs) are fully mechanical devices for the passive control, which is mainly composed of a tuned physical mass coupled to the parallel arrangement of a spring with a viscous fluid damper, which was proposed by Ormondroyd and Den Hartog over a hundred years ago [1,2]. Certainly, the vibration mitigation effectiveness of the DVAs strongly depends on both the tuned physical mass and the suspension system’s mechanical energy dissipation capability. To address this drawback, different variant design topologies of the DVA have been proposed, which are: the non-traditional DVA designed by Ren [3], Maxweel element-based DVA studied by Nishihara and Anh [4,5], Kelvin element-based DVA proposed by Kaul [6], as well as other layouts.
When the target is to suppress broadband vibration, the aforementioned devices lack both robust frequency filtering and transient and steady-state vibration mitigation effectiveness. To address with these concerns, the DVA’s performance has been improved by Asami [7,8] through the usage of multiple DVAs connected both in series and in parallel, and the Two-Degree-of-Freedom Tuned Mass Damper (TDOF-TMD) based on the stiff beam that undergoes translational and rotational dynamics which was analyzed by Zuo [9,10]. The engineering applications of these devices are only limited to the installation space, to mention a few: horizontal axis wind turbines [11,12], machining processes improvement [13], seismic vibration mitigation [14], as well as other substantial applications. In view of the vibration attenuation potential of these devices, the technology of multiple DVAs configured in series was hybridized by Barredo et al. [15] by means of the rotational inertia concept. This passive control technology is well known in the literature as The Inerter, which was proposed by Smith in 2002 [16,17].
The inerter is a mechanical device that stores kinetic energy through a flywheel, which has been studied by Chen et al. [18]. When such a mechanical energy is released, the inerter’s terminals provide reaction forces directly proportional to the product of the inertance value with the acceleration difference value of its terminals. Recently, Ma et al. [19] reported the three important dynamic characteristics of such a device, which are the following: a) frequency isolation capacity, b) inertial mass improvement and c) negative stiffness effect. It is worth mentioning that, since the invention of the inerter, many different investigations have been conducted on its dynamic performance for both stationary and non-stationary structures, which were reported by Wagg [20]. Although much research has been performed on the control performance for inerter-based DVAs considering different kinds of excitation sources, the control performance of DVA based on grounded inerter under base excitation has not yet been considered. In fact, it leads to the study of the inerter’s control effectiveness considering the frequency response function (FRF) of the force transmission from the structure to the mechanical structure’s foundation, which is one of the force transmissibility problems commonly reported in the literature [21]. Hence, in this paper the calibration process of the dimensionless transmissibility function is presented using the fixed-point technique (FPT) that is based on Krenk’s theory. Then, the
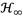and
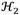criteria are proposed as dynamic performance measures for the performance evaluation of both harmonic and random vibration inputs. In the first instance, the double rack-pinion inerter’s operating principle and motion equation is presented with the aim of analytically explaining its operation mechanism, which was developed by the authors.
2. Theoretical mechanical models
Currently, there are several simple physical designs of the inerter, such designs are the following: the rack-pinion mechanism-based inerter, ball-screw type inerter and the last one based on the hydraulic transmission, among other modern inerters reported in [20,22]. In order to provide a greater rotational inertia, a double rack-pinion type inerter could be used, see. Fig. 1. The double rack-pinion type inerter is mainly composed of a rack that consists of teeth on both the top and bottom, a gear transmission system with a ratio of 2 to 1, and two flywheels.
In Fig. 1, f e (t), x 1 (t) and x 2 represent force input, rack’s displacement (terminal 1), and inerter’s terminal 2 displacement, respectively. With this in mind, the inerter’s dynamic equation can be easily obtained by applying the Euler-Lagrange formulism. By doing this, it results in the following:
where, b is the inerter’s inertance in units of kilograms, which can be increased either by changing the gear transmission ratio or increasing the flywheel’s rotational inertia. From eq. (1), the force exerted by the inerter is directly proportional to the acceleration difference
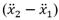of its terminals. In the next section, the inerter’s intrinsic dynamic properties are explained, and how they can improve the control performance of classic DVAs.
2.1. Inerter-based mechanical systems
In this section, the theoretical mathematical models are obtained when the inerter is coupled to the single and two degree-of-freedom mechanical systems, in order to reveal its vibration mitigation effectiveness in base-excited structures.
In Fig. 2, three undamped mechanical systems are described, of which b) and c) are of two degrees-of-freedom (DOF), while the first shown in a) is only of a single DOF. In addition, the dynamical system shown in Fig. 2 c) is analogous to the Tuned-Mass-Damper-Inerter (TMDI) [23]. Note that, the inerter’s terminals are strategically configured to reveal its operation principle, especially when the systems shown in Fig. 2 are subjected to the resonance. Indeed, it implies to analyze the dimensionless frequency response function (FRF) of the force that is transmitted towards the base of the primary structure. To achieve such a target, it is necessary to write the motion equations for each dynamical system in a dimensionless form, as described in eq. (2).
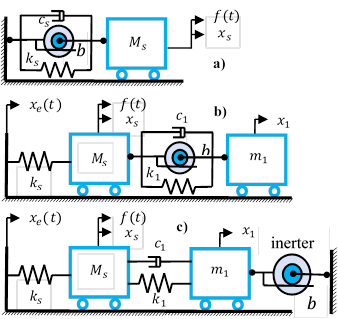
Source: Authors
Figure 2 The inerter coupled to single and two degrees-of-freedom mechanical systems. a) grounded inerter-based vibration isolator, b) ungrounded inerter-based DVA and c) grounded inerter-based DVA (TMDI).
From eq. (2), β is absorber to primary structure mass ratio, while μ is inertance to absorber’s physical mass ratio. Then, q is undamped circular frequency ratio. Furthermore,
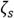and
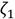are the damping factors for the primary structure and the absorber, respectively. Finally, Ω is the forced frequency ratio. It is worth mentioning that if the system shown in Fig. 2 a) is undamped, it is easy to determine its natural frequency ω
n
from the dimensionless eq. (2)-a). This results in:
Note that, if the inertance b increases in eq. (3), the primary structure’s natural frequency ω n decreases. It means that the inerter can modify the vibration isolator’s natural frequency, which allows it to work away of resonance. However, the primary system’s dynamic response increases by increasing the inerter’s inertance. This results in the inerter assisting the movement of the primary structure, providing a similar effect to that produced by the negative stiffness damper (NSD) [24,25]. In fact, this can be easily proved by applying the Fourier transform to the inerter’s dynamic equation. It gives the following equation:
From eq. (4), it is clear to note that the product - bω 2 results in negative stiffness physical units. This is one of the most inerter’s beneficial dynamic properties, which is worth exploiting in passive control systems. When the inerter’s terminals are not connected to the mechanical ground as shown in Fig. 2 b), it is not easy to qualitatively determine its control effect on the primary structure mass M s . Meanwhile, control effect for the grounded inerter-based DVA depicted in Fig. 2 c), which is intuitive as it will increase the DVA’s control force causing the primary structure’s dynamic response reduction. This will be revealed in the next section through a frequency calibration process based on the FPT.
3. Frequency calibration procedure
To apply the FPT, it is necessary to compute the transmissibility FRFs for the dynamic systems described in Fig. 2 b) and c). Such dimensionless functions can be computed by simultaneously solving the sets of eqs. (2) (b) and (c). By doing this, the following are obtained.
Note that, eq. (5) represents the dimensionless transmissibility FRF for the system shown in Fig. 2 (b), while the eq. (6) denotes that of the system depicted in Fig. 2 (c). Then the subfunctions of these FRFs can be written as follows:
The FPT basically consists of two operating modes of the absorber’s damper. The first mode is when the damping factor
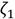approaches zero, which means that the resulting system becomes a two-DOF mechanical system with two undamped resonant frequencies. The second mode is when the damping factor
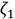approaches infinite value, which implies that the damper is blocked causing the masses m
1 and M
s
are virtually clamped together. By applying these conditions to the FRFs given by eqs. (5) and (6), the following are produced.
Considering the plus sign into eq. (7), the trivial solution for the dimensionless variable q is yielded. While the minus sign yields the transmissibility FRF’s invariant frequencies, see the first equation of the set of eq. (9). Additionally, these invariant frequencies can also be expressed in terms of the tuning magnitude |T b |, as described by the second equation of eq. (9).
Taking into consideration that the ratio
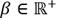, the biquadratic equations of eq. (9) yield positive real roots that are generally well known in the literature as dynamic system’s invariant frequencies [26]. The fixed-point technique holds that vibration amplitudes yielded at the transmissibility FRF’s invariant frequencies must be equal. To achieve this target, it is necessary to apply Vieta’s theorem to the set of equations of eq. (9). This leads to the calibration of the invariant frequencies by means of the optimal variable q which is given by the following mathematical expression.
In eq. (10), q b,ópt and |T b (β)| represent the optimal tuning frequency and the maximum tuning magnitude at the dynamical system’s invariant frequencies for the ungrounded inerter-based DVAs depicted in Fig. 2 (b). It is clear to see that the optimal fixed magnitude |T b (β)| is a monotonic function that increases when the inertance to the DVA’s physical mass ratio μ increases, meaning that the ungrounded inerter does not work well when connected between the masses m1 and M s . Note that the FPT quickly revealed the dynamic performance of the ungrounded inerter-based DVA. Now, it is also possible to reveal the performance for grounded inerter-based DVA by applying the EFP to eq. (8). It results in,
Eq. (11) reveals that the transmissibility FRF contains three invariant frequencies that can be denoted as
,
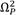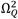and
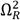. The existence of the third invariant frequency
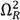does not directly allow the application of the FPT in a conventional way. Inspired by the methodology developed by Hu et al. [27], the invariant frequencies of eq. (11) can be written as follows.
The auxiliary equation that relates to the invariant frequencies
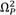and
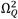is obtained when eq. (8) is evaluated at
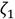→∞, creating the possibility to compute the optimal variable q. This equation is the following:
Both square invariant frequency
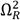and the optimal variable q
c,ópt
can be determined by combining the set of equations of eq. (12) together with that given by (13). By performing this, the following are yielded.
where,
Thus, the remaining invariant frequencies can be computed by substituting
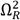into eq. (12). For the specific mass ratios β = 0.1 and μ = 1, the optimal tuning variable q
c,ópt
= 1.2028 is computed by eq. (14). Then, the three invariant frequencies for the grounded inerter-based DVA are described in Fig. 3.
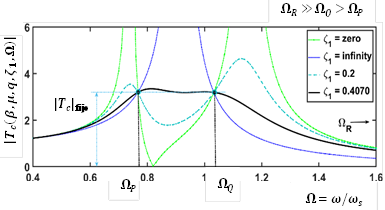
Source: Authors
Figure 3 Invariant frequencies and maximum tuning magnitude for the grounded inerter-based DVA’s dimensionless transmissibility FRF.
In Fig. 3, it is possible to note that the transmissibility FRF presents two well-calibrated invariant points which are both denoted as the optimal tuning magnitude |T
c
|fijo. Moreover, the invariant frequency
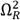is always higher than the
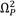and
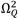. Based on this observation, in order to compute the optimal damping factor, the Krenk’s damping factor tuning technique is employed here [28]. This theory holds the existence of a singular frequency when the absorber’s dashpot is blocked, yielding a vibration amplitude must have the same vibration magnitude as those produced at the invariant frequencies
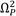and
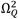. Because the analytical solution for the optimal damping factor
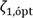is a very long rational mathematical expression, the optimal numerical values of such a solution are presented in Table 1 for the range of μ ∈ [0.5,2].
Table 1 Numerical solutions for both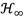 
and FPT
| a) ℋ∞ criterion | ||||||
|---|---|---|---|---|---|---|
| μ | qópt | 𝜁1,ópt | rmin | ℋ∞ norm | ||
| β = 0.1 | 0 | 0.9090 | 0.1854 | 0.9759 | 4.5891 | |
| 0.5 | 1.0760 | 0.2745 | 0.9633 | 3.7299 | ||
| 1 | 1.2023 | 0.3607 | 0.9506 | 3.2240 | ||
| 1.5 | 1.3023 | 0.4443 | 0.9379 | 2.8835 | ||
| 2 | 1.3838 | 0.5252 | 0.9252 | 2.6360 | ||
| b) Fixed-points technique | |𝑇𝑐|fijo | |||||
| β = 0.1 | 0 | 0.9090 | 0.2132 | --- | 4.5825 | |
| 0.5 | 1.0762 | 0.3124 | --- | 3.7103 | ||
| 1 | 1.2028 | 0.4070 | --- | 3.1944 | ||
| 1.5 | 1.3033 | 0.4973 | --- | 2.8465 | ||
| 2 | 1.3853 | 0.5837 | --- | 2.5939 | ||
Source: Authors
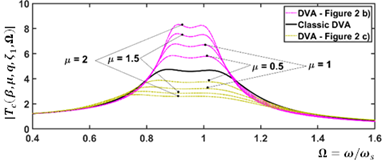
In order to differentiate the inerter’s control effect in the anti-vibration devices shown in Fig. 2 (b) and (c), it is necessary to perform a numerical simulation considering the optimal numerical solutions depicted in Table 1. By performing this, the undamped primary structure’s optimal FRF curves evolution is shown in Fig. 4.
Source: Authors
Figure 4 Optimal transmissibility FRF curves considering the mass ratio of the β = 0.1 and μ ∈ [0.5,2].
When observing the optimal transmissibility FRF curves in Fig. 4, the transmissibility FRF’s vibration amplitude increases for ungrounded inerter-based DVA coupled to the primary structure, while for the grounded inerter-based DVA decreases. This is mainly due to the inerter’s inertial mass amplification and the negative stiffness effects. Therefore, the classic DVA’s control performance can be improved by using a grounded inerter. To fairly assess the control performance for grounded inerter-based DVA, it is necessary to apply the performance measures
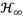and
.
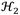4. Performance evaluation
To evaluate the vibration mitigation potential for anti-vibration systems subjected to both harmonic and random vibrations, many researchers often use control performance measures
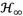and
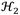. When the dynamical system is under harmonic vibration, the
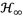criterion is more convenient to use than the
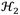criterion. In addition, 
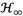criterion focuses on minimizing the control signal’s supreme value, meanwhile the
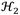criterion is used to minimize the total vibration energy into the system under random vibration [29].
4.1. ℋ∞ criterion
The transmissibility FRF’s supreme values for the grounded inerter-based DVA can be calculated through eq. (8), which basically represent the dynamical system’s resonant peaks. In the literature, it has been reported that the system’s best dynamic balance can be achieved when the resonant peaks reach the same Dynamic Magnification Factor (DMF) [30]. In order to achieve this dynamic trade-off between the resonant peaks, a constrained nonlinear multivariable optimization problem needs to be formulated herein,
Note that the nonlinear optimization problem given by formulation (17) can be numerically solved as in [31]. However, in order to achieve a high precision in the minimization process of the system’s resonant points, it is convenient to use the methodology recently developed by Asami et al. [32]. For two-DOF mechanical systems, Asami’s methodology holds that the primary structure’s FRF becomes a fourth-order algebraic equation
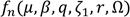in terms of
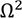when the magnitude |H
M
| is replaced by function
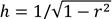. Now, by defining the control square resonant frequencies as
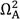and
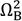, then
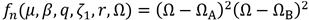. The variable Ω can be deleted by properly applying Vieta’s theorem, resulting in an overdetermined system with two nonlinear equations
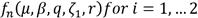. It is worth emphasizing that the overdetermined system provides a necessary condition, but not sufficient to yield a trade-off between the two resonant peaks. The remaining condition can be obtained by using the Jacobian matrix
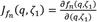of the infinitesimal variation of unknown variable r with respect to the design parameters
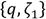. Then, the optimality criteria approach is satisfied when any 2x2 minor determinant of the Jacobian matrix is equalized zero. By calculating such a determinant, a constitutive equation is obtained that completes the conditions to solve the overdetermined system. Therefore, the objective function given by eq. (8) can be precisely minimized at two resonant peaks by solving the following set of nonlinear equations.
where
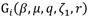for i = 1,..4 are rational functions described in Appendix A. Then, the set of nonlinear equations of eq. (18) can be solved through the Newton-Raphson method, considering the numerical solutions described in Table 1 as convergence initial points. For the sake of the fair comparison, a numerical simulation comparison between the FPT and
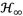criteria needs to be performed. By selecting the mass ratios β = 0.1 and μ = 1, the optimal FRFs are shown in Fig. 5.
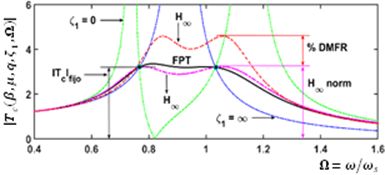
Source: Authors
Figure 5 Numerical comparison between the tuning FPT and the
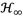criterion, considering the mass ratios β = 0.1 and μ = 1.
From Fig. 5, the maximum tuning magnitude |T
b
|fijo yielded at invariant frequencies is approximately equal to that produced at resonant frequencies which can be denoted as
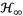norm, meaning that the FPT is an approximation to the
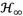optimization. Additionally, the percentage of the dynamic magnification factor reduction (%DMFR) is approximately 29.74% when the inerter’s inertial force effect is the same as that produced by the DVA’s physical mass. Indeed, it is evident that the grounded inerter’s intrinsic dynamic characteristics significantly improve the control performance of the classic DVA under harmonic vibration. When the system is subjected to random vibration, the optimal parameters change because the control objective is the minimization of the total vibration energy instead of resonant peaks. In this regard, the
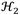criterion is more convenient than
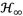norm.
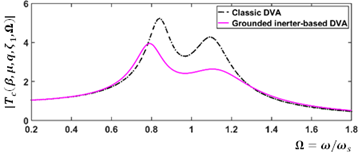
4.2. ℋ 2 criterion
The performance measure
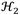is mainly based on the minimization of the expected value of the system’s dynamic response subjected to a stationary stochastic process whose power spectral density (PSD) is uniform at the whole excitation frequency band. Considering the input PSD of the signal x
e
(t) is
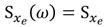, then the output PSD is
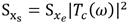. Therefore, the expected value is given by the following mathematical expression,
Note that eq. (17) represents the total vibrational energy of the dynamic system over the whole range of excitation frequencies, which can be expressed in a dimensionless form when the response |T
c
(ω)|2 becomes in
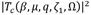[33]. It gives,
In eq. (18), the mathematical term
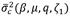is not only commonly known as the dimensionless variance of the system’s dynamic response, but also as the control performance index
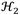[34]. Then, the improper integral can be calculated either by the integration method of residues [35] or obtaining the unique solution of the Lyapunov equation [36]. When the integration method of residues is applied in eq. (18), it becomes:
where,
It is easy to see that the rational function of the integrand of eq. (19) has four simple poles (Ω1, Ω2, Ω3 y Ω4) that are located in the upper middle part of the complex plane. Then, the residues yielded at each simple pole can be written as follows:
In eq. (21)
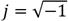is the imaginary unit. Then, the residues of eq. (21) can be simplified by using Vieta’s theorem, yielding the analytical mathematical expression for the dimensionless variance
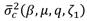given in terms of the coefficients described in eq. (20). It results in the following:
Finally, the dimensionless variance
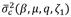is,
Now, it is necessary to formulate an unconstrained nonlinear multivariable optimization problem to minimize the dimensionless variance
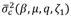, as follows:
The optimal variables qópt and
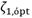satisfy to eq. (24), are obtained by solving the following set of nonlinear equations.
therefore,
The analytical solutions given by eq. (26) minimize the system’s total vibration energy, which also yields the significant reduction of the primary structure’s dynamic displacement. It is worth performing a numerical simulation to evaluate the control performance for the grounded inerter-based DVA considering the numerical solutions β = 0.1, μ = 1, qópt = 1.2856 and
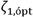= 0.3224, see Fig. 6.
Source: Authors
Figure 6 Optimal FRF curves computed via
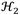criterion. The classic DVA’s optimal parameters are qópt = 0.9315 and
= 0.1525.
From Fig. 6, it is clear to observe that by increasing the inerter’s rotational inertia, the vibration amplitudes are considerably reduced. Therefore, the grounded inerter-based DVA can effectively mitigate random vibration and consequently reduces the energy transmitted to the foundation. In addition, the control performance
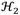can be calculated similarly as in [31], being approximately 33.03%.
5. Conclusion
In this work, the inerter’s dynamic was coupled to single and two DOF mechanical systems with the aim of revealing its control effect under harmonic and random vibrations. It was theoretically demonstrated by means of the FPT that the inerter does not provide a good control performance when its terminals are connected between the primary structure mass and that of the absorber, demonstrating a detrimental effect on the system’s dynamic response. However, when one of its terminals is connected to the ground and the another to the absorber mass, the inerter provides excellent control performance. To demonstrate the vibration attenuation effectiveness of the inerter device coupled to harmonically and randomly excited mechanical systems, the performance criteria
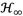and
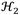were computed from formulation of the constrained and unconstrained nonlinear multivariable optimization problems. When the inerter’s inertial force effect is equal to that yielded by the absorber physical mass, the numerical solutions for the
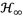criterion revealed that the grounded inerter-based DVA provides an improvement of approximately 29.74% in reducing the transmissibility FRF’s resonant peaks; whereas, the analytical solutions for
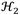criterion revealed a dynamic improvement of approximately 33.03% in minimizing the total vibration energy transmitted to the foundation. Therefore, the control performance of classic DVA can be significantly improved by the inerter’s inertial mass amplification and the negative stiffness effects.
