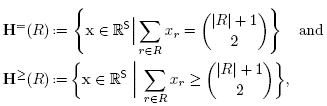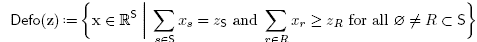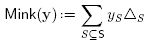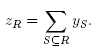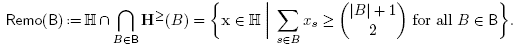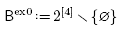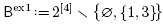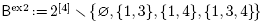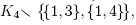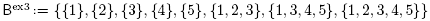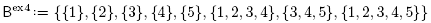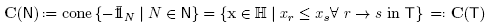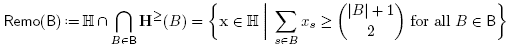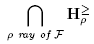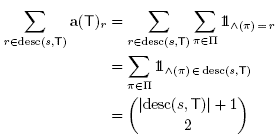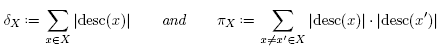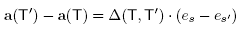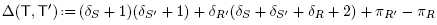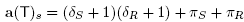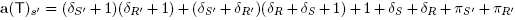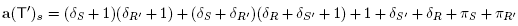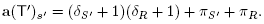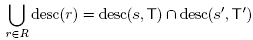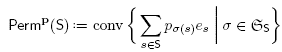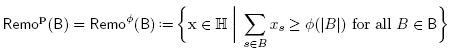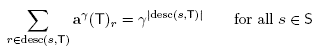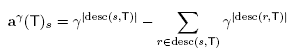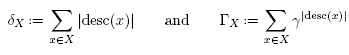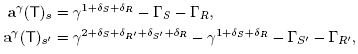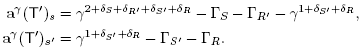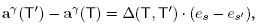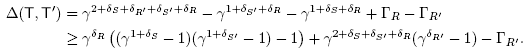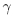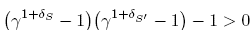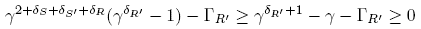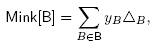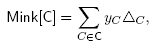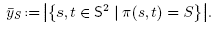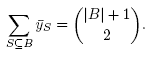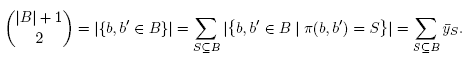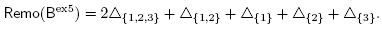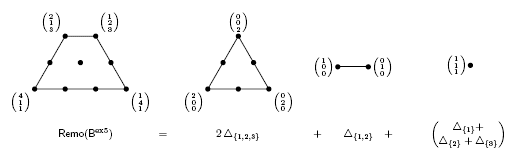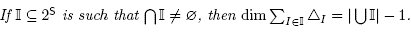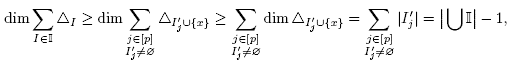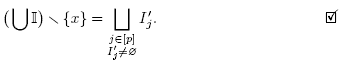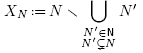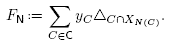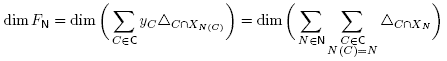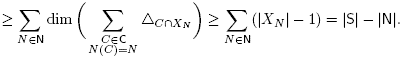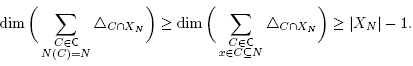1. Introduction
The permutahedron is a classical polytope related to various properties of the symmetric group. It is obtained as the convex hull of all permutations of [n] and its normal fan is the type A Coxeter fan. In [12], A. Postnikov defined generalized permutahedra as the polytopes obtained from the classical permutahedron by gliding its facets orthogonally to its normal vectors without passing any vertex. Equivalently [13], a generalized permutahedron is a polytope whose normal fan coarsens the type A Coxeter fan.
A particularly relevant example of generalized permutahedron is the associahedron constructed by S. Shnider and S. Sternberg ]14] and J.-L. Loday [9]. An associahedron is a polytope whose 1-skeleton realizes the rotation graph on binary trees with n vertices. The polytope of [14,9] is a remarkable realization of the associahedron which, besides being a generalized permutahedron, has the following three properties:
(i) it is obtained by deleting inequalities from the facet description of the permutahedron; we call such polytopes removahedra;
(ii) its vertex coordinates enumerate paths between leaves in the corresponding binary trees;
(iii) it is the Minkowski sum of the faces Δ I of the standard simplex given by all intervals I of [n].
This paper studies the connections between these three properties for a larger class of polytopes called nestohedra defined independently by A. Postnikov [12] and by E.-M. Feichtner and B. Sturmfels [4]. These polytopes extend the graph associahedra of M. Carr and S. Devadoss [2] as they realize the nested complex on an arbitrary building set, see Section 2.2 for definitions. All nestohedra are generalized permutahedra, but not necessarily removahedra. In this paper, we investigate which nestohedra can be realized as removahedra. We show that the nested complex of a connected building set closed under intersection can always be realized as a removahedron. For graph associahedra, this closure condition is equivalent to the underlying graph being chordful (i.e. any cycle induces a clique). Conversely, we show that the nested fan of a graphical building set is the normal fan of a removahedron if and only if the graph is chordful. We develop two complementary approaches to describe a nestohedron which is a removahedron. First, we show that its vertex coordinates can be computed by enumerating paths between leaves in building trees, exactly as in Point (ii) above. Second, we show that it decomposes into a simple Minkowski sum of faces of the standard simplex given by certain paths in the building set, which corresponds to the intervals of [n] in Point (iii) above.
2. Preliminaries
2.1. Permutahedra, deformed permutahedra, and removahedra
All polytopes considered in this paper are closely related to the braid arrangement and to the classical permutahedron. Therefore, we first recall the definition and basic properties of the permutahedron (see [16, Lect.0]) and certain relevant deformations of it. We fix a finite ground set S and denote by 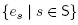 the canonical basis of
the canonical basis of 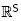 .
.
Definition 2.1. The permutahedron Perm(S) is the convex polytope obtained equivalently as
i. either the convex hull of the vectors 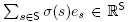 for all bijections a :
for all bijections a : 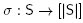 ,
,
ii. or the intersection of the hyperplane 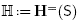 with the half-spaces H≥ (R) for Ø ≠ R C S, where
with the half-spaces H≥ (R) for Ø ≠ R C S, where
iii. or the Minkowski sum of all segments [e
r
, e
s
] for (r, s) 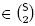 .
.
The normal fan of the permutahedron is the fan defined by the braid arrangement in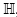 , i.e. the arrangement of the hyperplanes
, i.e. the arrangement of the hyperplanes 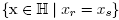 for r ≠ s Є S. Its k-dimensional cones correspond to the surjections from S to [k+1], or equivalently to the ordered partitions of S into k +1 parts. In this paper, we are interested in the following deformations of the permutahedron Perm(S). These polytopes were called generalized permutahedra by A. Postnikov [12,13], but we prefer the term deformed to distinguish from other natural generalizations of the permutahedron (to finite Coxeter groups, to removahedra, ...).
for r ≠ s Є S. Its k-dimensional cones correspond to the surjections from S to [k+1], or equivalently to the ordered partitions of S into k +1 parts. In this paper, we are interested in the following deformations of the permutahedron Perm(S). These polytopes were called generalized permutahedra by A. Postnikov [12,13], but we prefer the term deformed to distinguish from other natural generalizations of the permutahedron (to finite Coxeter groups, to removahedra, ...).
Definition 2.2 [ 12,13]. A deformed permutahedron is a polytope whose normal fan coarsens that of the permutahedron. Equivalently [13], it is a polytope defined as
for some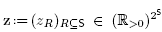 , such that
, such that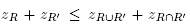 for any R, R' ⊆ S.
for any R, R' ⊆ S.
As the permutahedron itself, all deformed permutahedra can be decomposed as Minkowski sums and differences of dilates of faces of the standard simplex [1]. For our purposes, we only need here the following simpler fact, already observed in [12].
Remark 2.3
[
12]. For any S ⊆ S, we consider the face Δs: = conv 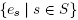 of the standard simplex Δs. For any y := (ys)
S ⊆S
where all ys are non-negative real numbers, the Minkowski sum
of the standard simplex Δs. For any y := (ys)
S ⊆S
where all ys are non-negative real numbers, the Minkowski sum
of dilated faces of the standard simplex is a deformed permutahedron Defo(z), and the values 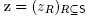 of the right hand sides of the inequality description of Mink(y) = Defo(z) are given by
of the right hand sides of the inequality description of Mink(y) = Defo(z) are given by
Remark 2.4. As the normal fan of a Minkowski sum is just the common refinement of the normal fans of its summands, and the normal fan is invariant by dilation, the combinatorics of the face lattice of the Minkowski sum Mink(y) only depends on the set 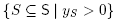 of non-vanishing dilation factors. When we want to deal with combinatorics only, we denote generically by Mink[C] any Minkowski sum Mink(y) with dilation factors y = (ys)
S ⊆S
such that
of non-vanishing dilation factors. When we want to deal with combinatorics only, we denote generically by Mink[C] any Minkowski sum Mink(y) with dilation factors y = (ys)
S ⊆S
such that 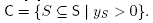
Among these deformed permutahedra, some are simpler than the others as all their facet defining inequalities are also facet defining inequalities of the classical permutahedron. In other words, they are obtained from the permutahedron by removing facets, which motivates the following name.
Definition 2.5. A removahedron is a polytope obtained by removing inequalities from the facet description of the permutahedron, i.e. a polytope defined for some B ⊆ 2s by
Our motivation to study removahedra is that they are completely determined by their normal fan (in fact even just by their normal vectors). In general, many relevant simplicial spheres (associahedra [9,5], graph associahedra [2], nestohedra [12,4], signed tree associahedra [11], Coxeter associahedra [6], accordion complexes [10],…) are easy to realize by fans that coarsen the normal fan of a zonotope (often the classical permutahedron, but also Coxeter permutahedra [6], or even other zonotopes [7,10]. Polytopal realization problems would thus be simpler if all these fans would be realized by removing the undesired facets of these zonotopes. This paper studies when this approach is possible for nestohedra.
2.2. Building set, nested complex, and nested fan
We now switch to building sets and their nested complexes. We only select from [2,12,4,15] the definitions needed in this paper. More details and motivation can be found therein.
Definition 2.6. A building set B on a ground set S is a collection of non-empty subsets of S such that
(B1) if B, B' Є B and B ∩ B' ≠ Ø, then B U B' Є B, and
(B2) B contains all singletons {s} for s Є S.
A building set is connected if S is the unique maximal element. Moreover, we say that a building set B is closed under intersection if B, B' Є B implies B ∩ B' Є B U{Ø}.
All building sets in this manuscript are assumed to be connected and we will study the relation between removahedra and building sets closed under intersection. We first recall a general example of building sets, arising from connected subgraphs of a graph.
Example 2.7. Given a graph G with vertex set S, we denote by BG the graphical building set on G, i.e. the collection of all non-empty subsets of S which induce connected subgraphs of G. The maximal elements of BG are the vertex sets of the connected components of G, and we will therefore always assume that the graph G is connected. We call a graph G chordful if any cycle of G induces a clique. Observe in particular that every tree is chordful. The following statement describes the graphical building sets of chordful graphs.
Lemma 2.8. A (finite connected) graph G is chordful if and only if its graphical building set is closed under intersection.
Proof. Assume that G is chordful, and consider B, B' Є B G and s, t Є B ∩ B'. As B and B' induce connected subgraphs of G, there exists paths P and P' between s and t in G whose vertex sets are contained in B and B', respectively. The symmetric difference PΔP' of these paths is a collection of cycles. Since G is chordful, we can replace in each of these cycles the subpath of P (resp. of P') by a chord. We thus obtain a path from s to t which belongs to B ∩ B'. It follows that B ∩ B' induces a connected subgraph of G and thus that B ∩ B' Є BG.
Assume reciprocally that G has a cycle 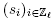 with a missing chord
with a missing chord 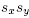 Consider the subsets
Consider the subsets 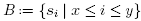 and
and 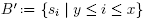 where the inequalities between labels in
where the inequalities between labels in  have to be understood cyclically. Clearly,
have to be understood cyclically. Clearly, 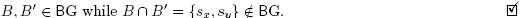
Example 2.9. The following sets are building sets:
The two building sets Bex0 and Bex2 are closed under intersection, while the other three are not.
In this paper, we focus on polytopal realizations of the nested complex of a building set, a simplicial complex defined below. Following [15] and contrarily to [12], we do not include S in the definition of B-nested sets.
Definition 2.10. A B-nested set N is a subset of B \ {S} such that
(N1) for any N, N ' Є N, either N ⊆ N ' or N' ⊆ N or N ∩ N ' = Ø, and
(N2) for any k ≥ 2 pairwise disjoint sets N 1 ,..., N k Є N, the union N 1∪…∪N k is not in B.
The B-nested complex is the simplicial complex N(B) of all B-nested sets.
Example 2.11. For a graphical building set BG, Conditions (N1) and (N2) in Definition 2.10 can be replaced by the following: for any N, N' Є N, either N ⊆ N' or N' ⊆ N or N U N' ∉BG. In particular, the BG-nested complex is a clique complex: a simplex belongs to B G if and only if all its edges belong to BG.
The B-nested sets can be represented by the inclusion poset of their elements. Since we only consider connected building sets, the Hasse diagrams of these posets are always trees. In the next definition, we consider rooted trees whose vertices are labeled by subsets of S. For any vertex v in a rooted tree T, we call descendant set of v in T the union desc(v, T) of the label sets of all descendants of v in T, including the label set of the vertex v itself. The B-nested sets are then in bijection with the following B-trees.
Definition 2.12. A B-tree is a rooted tree whose label sets partition S and such that
(1) for any vertex v of T, the descendant set desc(v, T) belongs to B,
(2) 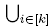 desc(v
i, T) is not in B for any k ≥ 2 incomparable vertices
desc(v
i, T) is not in B for any k ≥ 2 incomparable vertices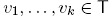 .
.
We denote by N(T) := {desc(v, T) | v vertex of T distinct from its root} the B-nested set corresponding to a B-tree T. Note that N (T) is a maximal B-nested set if and only if all the vertices of T are labeled by singletons of S. We then identify a vertex of T with the element of S labeling it.
The B-nested sets and the B-trees naturally encode a geometric representation of the B-nested complex as a complete simplicial fan. In the next definition, we define 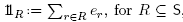 ,and we denote by
,and we denote by 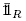 the projection of
the projection of 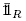 to
to 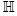 orthogonal to
orthogonal to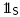 . Moreover, we consider
. Moreover, we consider 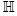 as a linear space.
as a linear space.
Definition 2.13. The B-nested fan (B) is the complete simplicial fan of
(B) is the complete simplicial fan of  := H=(S) with a cone
:= H=(S) with a cone
for each B-nested set N and B-tree T with N = N (T).
The B-nested fan is the normal fan of various deformed permutahedra (see Definition 2.2). We want to underline two relevant examples:
(i) the deformed permutahedron Defo(z) with right hand side
defined by
if R Є B and
otherwise, see [3];
(ii) the Minkowski sum Mink(
) of the faces of the standard simplex corresponding to all the elements of the building set B, see [12, Section 7].
However, these two realizations are not always removahedra. In general, the support functions realizing the normal fan  (B) can be characterized by local conditions [15, Proposition 6.3], but it is difficult to use these conditions to characterize which nested complexes can be realized as removahedra. In this paper, we adopt a different approach.
(B) can be characterized by local conditions [15, Proposition 6.3], but it is difficult to use these conditions to characterize which nested complexes can be realized as removahedra. In this paper, we adopt a different approach.
2.3. Results
The objective of this paper is to discuss necessary and sufficient conditions for the B-nested fan to be the normal fan of a removahedron (see Definition 2.5), and to study some properties of the resulting removahedra (vertex description, Minkowski sum decomposition). We thus consider the removahedron Remo(B) described by the facet defining inequalities of the permutahedron Perm(S) whose normal vectors are rays of the B-nested fan, i.e.
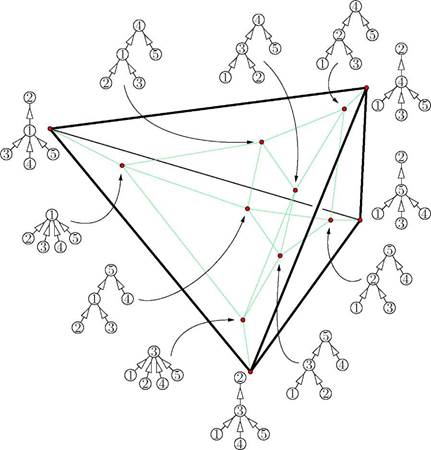
Example 2.14.Figure 1 represents the removahedra Remo(Bex0), Remo(Bex1) and Remo(Bex2) corresponding to the graphical building sets Bex0, Bex1 and Bex2 of Example 2.9. Observe that Remo(Bex0) and Remo(Bex2) realize the corresponding nested complexes, whereas Remo(Bex1) is not even a simple poly-tope.
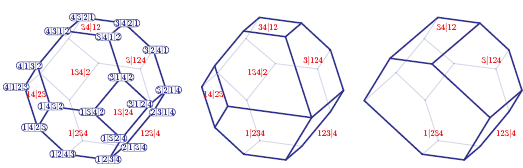
Figure 1 The 3-dimensional permutahedron Perm[4] = Remo(Bex0) and the removahedra Remo(Bex1) and Remo(Bex2).
We want to understand when does Remo(B) realize the nested complex N(B). The following statement provides a general sufficient condition.
Theorem 2.15.
If
B
is a connected building set closed under intersection, then the normal fan of the removahedron
Remo(B)
is the B-nested fan
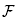 (B).
In particular,
Remo(B)
is a simple polytope.
(B).
In particular,
Remo(B)
is a simple polytope.
We provide two different complementary proofs of this result, which both show relevant by-product properties of these removahedra:
(i) In Section 3, we apply a result from [6] which characterizes the valid right hand sides to realize a complete simplicial fan as the normal fan of a convex polytope. For this, we first compute for each maximal B-tree T the intersection point a(T) of all facet defining hyperplanes of Remo(B) normal to the rays of the cone C(T). This provides along the way relevant formulas for the vertex coordinates of the corresponding vertex of the removahedron Remo(B). We then show that the vector joining the points a(T) and a(T') corresponding to two adjacent cones C(T) and C(T') indeed points in the right direction for Remo( B) to realize the nested fan
(B).
(ii) In Section 4, we show that certain Minkowski sums of dilated faces of the standard simplex realize the B-nested fan as soon as all B-paths appear as summands. We then find the appropriate dilation factors for the resulting polytope to be a removahedron.
Relevant examples of application of Theorem 2.15 arise from graphical building sets of chordful graphs. If we restrict to graphical building sets, Lemma 3.6 shows that chordfulness of G is also a necessary condition for the BG-nested fan 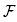 (BG) to be the normal fan of Remo(BG). We therefore obtain the following characterization of the graphical building sets whose nested fan is the normal fan of a removahedron. This characterization is illustrated by Example 2.14.
(BG) to be the normal fan of Remo(BG). We therefore obtain the following characterization of the graphical building sets whose nested fan is the normal fan of a removahedron. This characterization is illustrated by Example 2.14.
Theorem 2.16.
The BG-nested fan
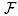 (BG) is the normal fan of the removahedron Remo(BG) if and only if the graph G is chordful.
(BG) is the normal fan of the removahedron Remo(BG) if and only if the graph G is chordful.
Example 2.17. Specific families of chordful graphs provide relevant examples of graph associahedra realized by removahedra, e.g.:
In contrast, for the cycle associahedra, aka. cyclohedra, the nested fan 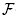 (BOn) is not the normal fan of a removahedron since the cycle On is not chordful for n ≥ 4.
(BOn) is not the normal fan of a removahedron since the cycle On is not chordful for n ≥ 4.
To conclude, we observe that a general building set B does not need to be closed under intersection for the removahedron Remo(B) to realize the B-nested fan  (B). In fact, our first proof of Theorem 2.15 shows the following refinement. We say that two building blocks B, B' Є B are exchangeable if there exists two maximal B-nested sets N, N' such that N \ {B} = N' \ {B'}.
(B). In fact, our first proof of Theorem 2.15 shows the following refinement. We say that two building blocks B, B' Є B are exchangeable if there exists two maximal B-nested sets N, N' such that N \ {B} = N' \ {B'}.
Theorem 2.18. If the intersection of any two exchangeable building blocks of B also belongs to B, then the normal fan of the removahedron Remo(B) is the B -nested fan F(B).
This result is illustrated by the building set Bex3 of Example 2.9 and its removahedron Remo(Bex3) represented in Figure 2. However, the condition of Theorem 2.18 is still not necessary for the removahedron Remo(B) to realize the nested complex N(B). For example, we invite the reader to check that the removahedron Remo(Bex4) of the building set Bex4 of Example 2.9 realizes the corresponding nested complex, even if {1, 2, 3,4} ∩ {3, 4, 5} = {3, 4} ∉ Bex4 while {1 , 2, 3, 4} and {3, 4, 5} are exchangeable. Corollary 3.4 gives a necessary and sufficient, thought unpractical, condition for the removahedron Remo(B) of an arbitrary building set B to realize the nested fan  (B).
(B).
3. Counting paths in maximal B-trees
Our first approach to Theorem 2.15 is the following characterization of the valid right hand sides to realize a complete simplicial fan as the normal fan of a convex polytope. A proof of this statement can be found e.g. in [6, Th. 4.1].
Theorem 3.1 ([6, Theorem 4.1]). Given a complete simplicial fan in
in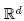 , consider for each ray p of
, consider for each ray p of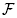 a half-space
a half-space 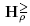 of
of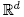 containing the origin and defined by a hyperplane
containing the origin and defined by a hyperplane 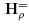 orthogonal to p. For each maximal cone C of
orthogonal to p. For each maximal cone C of 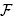 , let a(C) Є
, let a(C) Є 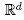 be the intersection of the hyperplanes
be the intersection of the hyperplanes 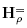 for p Є C. Then the following assertions are equivalent:
for p Є C. Then the following assertions are equivalent:
(i) The vector a(C')-a(C) points from C to C' for any two adjacent maximal cones C, C' of
.
(ii) The polytopes
coincide and their normal fan is 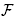 .
.
Since we are given a complete simplicial fan 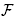 (B) and we want to prescribe the right hand sides of the inequalities to describe a polytope realizing it, we are precisely in the situation of Theorem 3.1. Our first step is to compute the intersection points of the hyperplanes normal to the rays of a maximal cone of
(B) and we want to prescribe the right hand sides of the inequalities to describe a polytope realizing it, we are precisely in the situation of Theorem 3.1. Our first step is to compute the intersection points of the hyperplanes normal to the rays of a maximal cone of 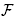 (B). We associate to any maximal B-tree T a point a(T) Є
(B). We associate to any maximal B-tree T a point a(T) Є 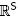 whose coordinate a(T)s is defined as the number of paths n in T such that s is the topmost vertex Λ(Π) of Π in T. Note that all coordinates of a(T) are strictly positive integers since we always count the trivial path reduced to the vertex s of T. The following lemma ensures that the point a(T) lies on all hyperplanes of Remo(B) normal to the rays of the cone C(T).
whose coordinate a(T)s is defined as the number of paths n in T such that s is the topmost vertex Λ(Π) of Π in T. Note that all coordinates of a(T) are strictly positive integers since we always count the trivial path reduced to the vertex s of T. The following lemma ensures that the point a(T) lies on all hyperplanes of Remo(B) normal to the rays of the cone C(T).
Lemma 3.2. For any maximal B-tree T and any element s Є S, the point a(T) lies on the hyperplane H = (desc(s, T)).
The proof of this lemma is inspired from similar statements in [8, Proposition 6] and [11, Proposition 60]. Although the latter covers the present result, we provide a simpler and self-contained proof for the convenience of the reader.
Proof of Lemma 3.2. Consider a B-tree T, and let ∏ be the set of all paths in T. For any ΠЄ∏ , the topmost vertex Λ(Π) of Π in T is a descendant of s in T if and only if both endpoints of Π are descendants of s in T. It follows that
since the number of paths Π Є ∏ such that Λ(Π) Є desc(s, T) is just the number of pairs of endpoints in desc(s, T), with possible repetition. We therefore have a(T) Є H=(desc(s, T)). 
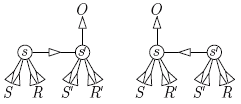
Guided by Theorem 3.1, we now compute the difference a(T') - a(T) for two adjacent maximal B-trees T and T'. Let s, s' Є S be such that the cones C(T) and C(T') are separated by the hyperplane of equation 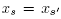 , and moreover
, and moreover 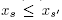 in C(T) while
in C(T) while 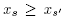 in C(T'). Let
in C(T'). Let  denote the tree obtained by contracting the arc
denote the tree obtained by contracting the arc  in T or, equivalently, the arc
in T or, equivalently, the arc 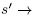 s in T'. Since both T and T' contract to
s in T'. Since both T and T' contract to 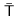 , the children of the node of
, the children of the node of 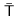 labeled by {s, s'} are all children of s or s' in both T and T'. We denote by S (resp. by S') the elements of S which are children of s (resp. of s') in both T and T'. In contrast, we let R denote the elements of S which are children of s in T and of s' in T', and R' those which are children of s' in T and of s in T'. These notations are summarized on Figure 3. For r Є S U S' U R U R', we denote the set of descendants of r by desc(r) := desc(r, T) = desc(r, T') = desc(r,
labeled by {s, s'} are all children of s or s' in both T and T'. We denote by S (resp. by S') the elements of S which are children of s (resp. of s') in both T and T'. In contrast, we let R denote the elements of S which are children of s in T and of s' in T', and R' those which are children of s' in T and of s in T'. These notations are summarized on Figure 3. For r Є S U S' U R U R', we denote the set of descendants of r by desc(r) := desc(r, T) = desc(r, T') = desc(r, 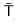 ).
).
Lemma 3.3. Let B be a building set and T, T' be two adjacent maximal B-trees. Using the notation just introduced, we set
for X Є {S, S', R, R'}. Then the difference a(T') - a(T) is given by
where the coefficient Δ(T, T') is defined by
Proof. By definition of the coordinates of a(T), we compute
and
Moreover, the coordinates a(T)
r
and a(T')r coincide if 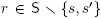 since the flip from T to T' did not affect the children of the node r. The result immediately follows.
since the flip from T to T' did not affect the children of the node r. The result immediately follows. 
Combining Theorem 3.1 and Lemmas 3. and 3.3, we thus obtain the following characterization.
Corollary 3.4. The B-nested fan 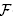 (B)
is the normal fan of the removahedron
Remo(B)
if and only if
Δ(T, T') > 0 for any pair of adjacent maximal B
-trees
T, T'
.
(B)
is the normal fan of the removahedron
Remo(B)
if and only if
Δ(T, T') > 0 for any pair of adjacent maximal B
-trees
T, T'
.
The following lemma gives a sufficient condition for this property to hold.
Lemma 3.5. For any two adjacent maximal B-trees T, T' as in Lemma 3.3, if desc(s, T) ∩ desc(s', T') belongs to B U {Ø}, then Δ(T, T') > 0.
Proof. By assumption, the set
either belongs to the building set B or is empty. Since desc(r) ∩ desc(r') = Ø for r ≠ r' Є R and desc(r) Є B for r Є R, we conclude that |R| ≤ 1 by Condition (N2) in Definition 2.10. Thus 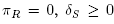 and
and 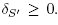 The statement follows.
The statement follows. 
It follows that if B is closed under intersection of exchangeable elements, then the B-nested fan  (B) is the normal fan of the removahedron Remo(B). This concludes our first proof of Theorems 2.15 and 2.18. For graphical building sets, we conclude from Lemma 2.8 that Remo(BG) realizes
(B) is the normal fan of the removahedron Remo(B). This concludes our first proof of Theorems 2.15 and 2.18. For graphical building sets, we conclude from Lemma 2.8 that Remo(BG) realizes  (B) as soon as G is chordful. Conversely, the following lemma shows that the condition of Corollary 3.4 is never satisfied for building sets of non chordful graphs, thus concluding the proof of the characterization of Theorem 2.16.
(B) as soon as G is chordful. Conversely, the following lemma shows that the condition of Corollary 3.4 is never satisfied for building sets of non chordful graphs, thus concluding the proof of the characterization of Theorem 2.16.
Lemma 3.6. Let G be a connected graph that is not chordful. Then there exist two adjacent maximal BG-trees T, T' such that Δ(T, T') ≤ 0.
Proof. Consider a cycle O in G not inducing a clique and choose two vertices a, b Є O not connected by a chord. As a and b are not connected, {{a}, {b}} is a B-nested set. We complete it to a B-nested set  formed by subsets of O all containing either a or b, such that
formed by subsets of O all containing either a or b, such that  be maximal for this property. Let B
a
and B
b
denote the maximal elements of
be maximal for this property. Let B
a
and B
b
denote the maximal elements of  containing a and b, respectively. By maximality of
containing a and b, respectively. By maximality of  , all remaining vertices in O \ (Ba U Bb) are connected to both Ba and Bb. Moreover, there are at least two such vertices s, s'. Consider two maximal B-nested sets N and N' both containing
, all remaining vertices in O \ (Ba U Bb) are connected to both Ba and Bb. Moreover, there are at least two such vertices s, s'. Consider two maximal B-nested sets N and N' both containing 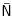 and B
a
U B
b
U {s, s'}, and such that N contains
and B
a
U B
b
U {s, s'}, and such that N contains 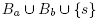 and N' contains
and N' contains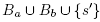 . The corresponding B-trees T and T
'
are such that node s
'
covers s in T and s covers s
'
in T
'
. Moreover, using the notations introduced earlier in this section, R' = S = S' = Ø while
. The corresponding B-trees T and T
'
are such that node s
'
covers s in T and s covers s
'
in T
'
. Moreover, using the notations introduced earlier in this section, R' = S = S' = Ø while 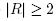 as R contains one vertex of Ba and one of Bb. Thus
as R contains one vertex of Ba and one of Bb. Thus 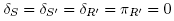 and
and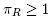 , which implies Δ(T, T') ≤ 0.
, which implies Δ(T, T') ≤ 0. 
As already observed earlier, for general building sets, the condition of Lemma 3.5 is not necessary for Remo(BG) to realize F( B). For example, in the building set Bex4 of Example 2.9, the building blocks {1, 2, 3, 4} and {3, 4, 5} are exchangeable but {1, 2, 3, 4} n {3,4, 5} = {3,4} € Bex4. However, {1, 2, 3, 4} and {3,4, 5} are the only two intersecting exchangeable building blocks of Bex4, and for any two maximal Bex4-trees T, T such that N(T) \ {{1, 2, 3,4}} = N(T') \ {{3, 4, 5}}, we have A(T, T') = 1. Therefore, Corollary 3.4 ensures that Remo(Bex4) realizes 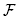 (Bex4).
(Bex4).
Remark 3.7. The arguments of this first proof of Theorems 2.15 and 2.18 can be used to show that any nestohedron can be realized as a skew removahedron. A skew permutohedron is the convex hull
of the orbit of a generic point p Є  under the action of the symmetric group
under the action of the symmetric group 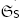 on
on 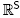 by permutation of coordinates. Equivalently, a skew permutahedron is the deformed permutahedron Perm
by permutation of coordinates. Equivalently, a skew permutahedron is the deformed permutahedron Perm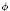 (S) := Defo(
(S) := Defo(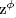 ) for a right hand side :=
) for a right hand side := 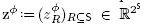 defined by
defined by 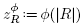 for function
for function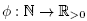 . For example, the classical permutahedron Perm(S) is the permutahedron Perm
. For example, the classical permutahedron Perm(S) is the permutahedron Perm (S) for
(S) for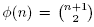 . A skew removahedron is a polytope
. A skew removahedron is a polytope
obtained by removing inequalities from the facet description of a skew permutahedron Permp(S) =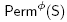 . Note that even if skew removahedra have much more freedom than classical removahedra, they do not contain all deformed permutahedra.
. Note that even if skew removahedra have much more freedom than classical removahedra, they do not contain all deformed permutahedra.
A consequence of the realization of [3] is that all graph associahedra can be realized as skew removahedra, namely by removing facets of the skew permutahedron 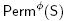 for
for 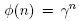 with
with 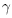 > 2. The arguments presented in this Section provide an alternative proof of this result and extend it to all nestohedra. Let us quickly give the proof here.
> 2. The arguments presented in this Section provide an alternative proof of this result and extend it to all nestohedra. Let us quickly give the proof here.
For a B-tree T, consider the point 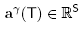 defined by
defined by
We do not need to compute explicitly the coordinates of 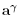 (T). We will only use that for any s Є S,
(T). We will only use that for any s Є S,
Consider now two adjacent maximal B-trees T, T' with the same notations as in Figure 3. For a subset X Є {S,S',R,R'}, define
Using these notations, we compute:
and
Moreover, the coordinates a(T)r and a(T')r coincide if r Є S \ {s, s'} since the flip from T to T' did not affect the children of the node r. We therefore obtain
since 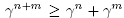 for 1 ≤ n,m. We therefore obtain that Δ(T, T') > 0 and we conclude by Theorem 3.1.
for 1 ≤ n,m. We therefore obtain that Δ(T, T') > 0 and we conclude by Theorem 3.1.
4. Minkowski sums
In this section, we provide an alternative proof that any building set closed under intersection can be realized as a removahedron. The approach of this section is complementary to the previous one since it focusses on Minkowski sums. As illustrated by the following statement observed independently by A. Postnikov [12, Section 7] and E.-M. Feichtner and B. Sturmfels [4], Minkowski sums provide a powerful tool to realize nested complexes.
Theorem 4.1 [12, Section 7], [4]. For any building set B,
the B-nested fan
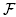 (B)
is the normal fan of the Minkowski sum
(B)
is the normal fan of the Minkowski sum
where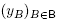 are arbitrary strictly positive real numbers, and Δ
B
denotes the face of the standard simplex corresponding to B.
are arbitrary strictly positive real numbers, and Δ
B
denotes the face of the standard simplex corresponding to B.
Remember from Remark 2.4 that the normal fan, and thus the combinatorics, of the Minkowski sum Mink[B] only depends on B, not on the values of the dilation factors 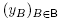 (as soon as all these values are strictly positive). These Minkowski sums Mink[B] are deformed permutahedra, but not necessarily removahedra. In this section, we relax Theorem 4.1 to give a sufficient condition for a subsum of Mink[B] to keep the same normal fan, and prove that a well-chosen subsum of Mink[B] is indeed a removahedron.
(as soon as all these values are strictly positive). These Minkowski sums Mink[B] are deformed permutahedra, but not necessarily removahedra. In this section, we relax Theorem 4.1 to give a sufficient condition for a subsum of Mink[B] to keep the same normal fan, and prove that a well-chosen subsum of Mink[B] is indeed a removahedron.
4.1. Generating sets and building paths
We say that a subset C of B is generating if for each B Є B and for each b G B, the set B is the union of the sets C Є C such that b Є C ⊆ B. The following statement can be seen as a relaxation of Theorem 4.1: it shows that the Minkowski sum Mink[C] of the faces of the standard simplex over a generating subset C of B still has the same normal fan as the Minkowski sum Mink[B] itself. Note that we do not make here any particular assumption on the building set B. The proof, adapted from that of [12, Theorem 7.4], is delayed to the next section.
Theorem 4.2.
If
C
is a generating subset of a connected building set B, then the B-nested fan
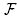 (B)
is the normal fan of the Minkowski sum
(B)
is the normal fan of the Minkowski sum
where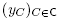 are arbitrary strictly positive real numbers.
are arbitrary strictly positive real numbers.
Example 4.3. Given a connected graph G, the set CG of all vertex sets of induced subpaths of G is a generating subset of the graphical building set BG. Set here yC = 1 for all C Є CG. Then
(1) if G = P is a path, then BP and CP coincide and Mink[BP] = Mink[CP] is precisely the associahedron of [ 14,9 ] ;
(2) if G = T is a tree, then Mink[CT] is the (unsigned) tree associahedron of [ 11 ] ;
(3) if G = K s is the complete graph, then
while CKs =
. Thus, Mink[CKs] is the classical permutahedron, while Mink[BKs] is a dilated copy of it.
In fact, the notion of paths can be extended from these graphical examples to the more general setting of connected building sets closed under intersection. Throughout the end of this section, we consider a building set B on the ground set S, closed under intersection. For any R ⊆ S, we define the B-hull of R to be the smallest element of B containing R (it exists since B is closed under intersection). In particular, for any s,t Є S, we define the B-path Π(s,t) to be the B-hull of {s,t}. We denote by ∏(B) the set of all B-paths.
Example 4.4. For a graphical building set BG, the BG-paths are precisely the induced subpaths of G, i.e. with our notations ∏(BG) = CG.
Lemma 4.5. The set ∏ (B) of all B-paths is a generating subset of B.
Proof.
Let B Є B and b Є B. For any b' Є B, the path Π(b, b') contains b and is contained in B (indeed, B contains both b and b' and thus Π (b, b') by minimality of the latter). Therefore, b' belongs to the union of the sets C Є ∏(B) such that b Є C ⊆ B. The lemma follows by definition of generating subsets. 
In fact, the set of paths ∏(B) is the minimal generating subset of B, in the following sense.
Lemma 4.6. Any generating subset of B contains ∏(B).
Proof. Consider a generating subset C of B, and s,t G S. The B-path Π(s,t) is the smallest building block containing {s,t}. Therefore, Π(s,t) has to be in C, since otherwise t would not belong to the union of the sets C such that s Є C ⊆ Π (s,t) 
From Theorem 4.2 and Lemma 4.5, we obtain that any Minkowski sum Mink[∏(B)] is a realization of the B-nested complex. We now have to choose properly the dilation coefficients to obtain a removahedron. For S ⊆ S, define the coefficient
Lemma 4.7. The dilation coefficients 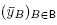 satisfy the following properties:
satisfy the following properties:
(i)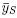 > 0 for all S Є ∏(B),
and
> 0 for all S Є ∏(B),
and
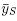 = 0 otherwise.
= 0 otherwise.
(ii) For all B Є B,
Proof.
Point (i) is clear by definition of the coefficients 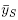 . We prove Point (ii) by double counting: for any B Є B and any b,b' Є B (distinct or not), the path n(b, b') is included in B. We can therefore group pairs of elements of B according to their B -paths:
. We prove Point (ii) by double counting: for any B Є B and any b,b' Є B (distinct or not), the path n(b, b') is included in B. We can therefore group pairs of elements of B according to their B -paths:
Combining Theorem 4.2 with Lemmas 4.5 and 4.7, we obtain an alternative proof of Theorem 2.15.
Corollary 4.8. For a building set b closed under intersection, the removahedron Remo(B) coincides with the Minkowski sum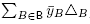 , and its normal fan is the B-nested fan.
, and its normal fan is the B-nested fan.
Remark 4.9. For a graphical building set BG of a chordful graph G, the coefficients 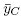 are all equal to 1 for all subpaths C Є CG. It is not anymore true for arbitrary buildin{g sets closed under intersect}ion. For example, consider the building set
are all equal to 1 for all subpaths C Є CG. It is not anymore true for arbitrary buildin{g sets closed under intersect}ion. For example, consider the building set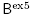 := {{1}, {2}, {3}, {1, 2}, {1, 2, 3}}, for which we obtain
:= {{1}, {2}, {3}, {1, 2}, {1, 2, 3}}, for which we obtain
This Minkowski decomposition is illustrated in Figure 4.
4.2. Proof of Theorem 4.2
This section is devoted to the proof of Theorem 4.2. We start with the following technical lemma on the affine dimension of Minkowski sums.
Lemma 4.10.
(i) Let
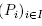 be polytopes lying in orthogonal subspaces of
be polytopes lying in orthogonal subspaces of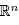 Then
Then
Proof. Point (i) is immediate as the union of bases of the linear spaces generated by the polytopes Pi is a basis of the linear space generated by 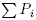 . For Point (ii), fix
. For Point (ii), fix 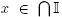 and an arbitrary order I1,…,I
p
. on
and an arbitrary order I1,…,I
p
. on 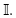 Define
Define 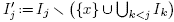 . We then have
. We then have
where the first inequality holds since 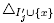 is a face of
is a face of 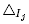 , the second one is a consequence of Point (i), and the last equality holds since we have the partition
, the second one is a consequence of Point (i), and the last equality holds since we have the partition
Proof of Theorem 4.2. Let C be a generating subset of a connected building set B, let 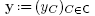 be strictly positive real numbers, let
be strictly positive real numbers, let 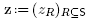 be defined by
be defined by 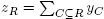 , and consider the polytope Mink(y) = Defo(z).
, and consider the polytope Mink(y) = Defo(z).
Let T be a B-tree and N := N(T) be the corresponding B-nested set. For N Є N, let
denote the label corresponding to N in the B-tree T, so that 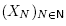 partitions S.
partitions S.
For C Є C, we define N(C) to be the inclusion maximal element N of N such that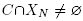 . Note that this element is unique: otherwise, the union of the maximal elements N Є N such that
. Note that this element is unique: otherwise, the union of the maximal elements N Є N such that 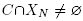 would be contained in B, thus contradicting Condition (N2) in Definition 2.10. Observe also that N(C) is the inclusion minimal element N of N such that C ⊆ N.
would be contained in B, thus contradicting Condition (N2) in Definition 2.10. Observe also that N(C) is the inclusion minimal element N of N such that C ⊆ N.
We now define
We will show below that FN is a face of Mink(y) whose normal cone is precisely the cone C(N). The map 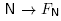 thus defines an anti-isomorphism from the nested complex
thus defines an anti-isomorphism from the nested complex 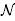 (B) to the face lattice of Mink(y).
(B) to the face lattice of Mink(y).
Consider any vector f := 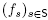 in the relative interior of the cone C(N). This implies that
in the relative interior of the cone C(N). This implies that 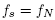 is constant on each N Є N, and
is constant on each N Є N, and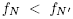 , for N,N'
Є
N
with
, for N,N'
Є
N
with 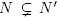 '.Let
'.Let 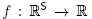 be the linear functional defined by
be the linear functional defined by 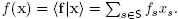 Since N(C) is the inclusion maximal element N of N such that
Since N(C) is the inclusion maximal element N of N such that 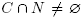 and
and 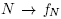 is increasing, the face of
is increasing, the face of 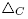 maximizing
maximizing  is precisely
is precisely 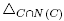 . It follows that F
N is the face maximizing
. It follows that F
N is the face maximizing 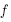 on Mink(y), since the face maximizing
on Mink(y), since the face maximizing 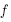 on a Minkowski sum is the Minkowski sum of the faces maximizing
on a Minkowski sum is the Minkowski sum of the faces maximizing 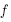 on each summand. We conclude that F
N is a face of Mink(y) whose normal cone contains at least C(N ), and therefore that the map
on each summand. We conclude that F
N is a face of Mink(y) whose normal cone contains at least C(N ), and therefore that the map 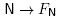 is a poset anti-homomorphism.
is a poset anti-homomorphism.
To conclude, it is now sufficient to prove that the dimension of F
N is indeed |S| - |N|. The inequality dim 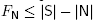 is clear since the normal cone of F
N contains the cone C(N). To obtain the reverse inequality, observe that
is clear since the normal cone of F
N contains the cone C(N). To obtain the reverse inequality, observe that
The first inequality holds by Lemma 4.10 (i) since the X N are disjoints. The second inequality follows from the assumption that C is a generating subset of B. Indeed, fix N Є N and pick an element x Є X N . Observe that if C Є C is such that x Є C ⊆ N, then N(C) = N. Moreover, since N is the union of the elements C Є C such that x Є C ⊆ N, we obtain that X N is the union of the sets C∩X N over the elements C Є C such that x Є C ⊆ N. By Lemma 4.10 (ii), this implies that
This concludes the proof that the dimension of F
N is given by |S| - |N|, and thus that the map 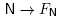 is an anti-isomorphism.
is an anti-isomorphism.