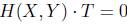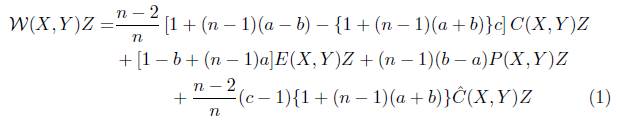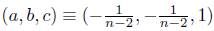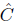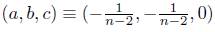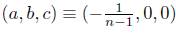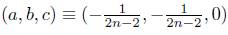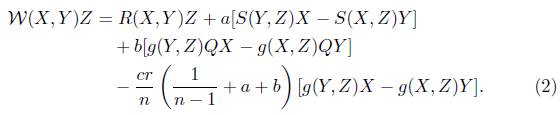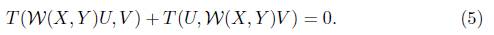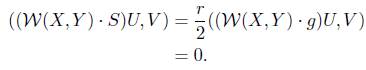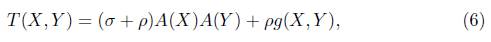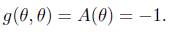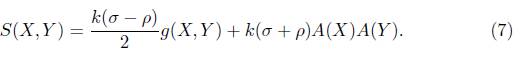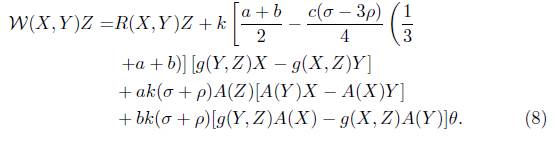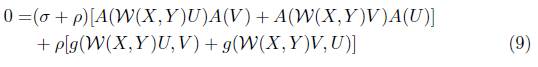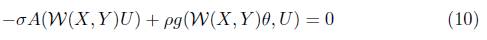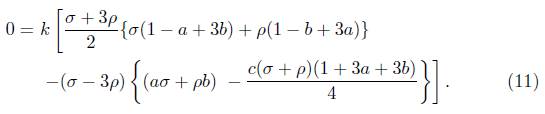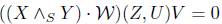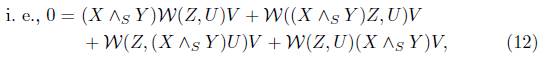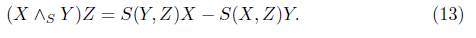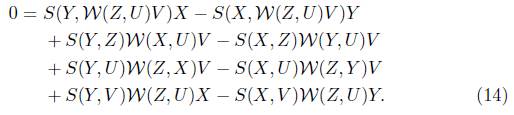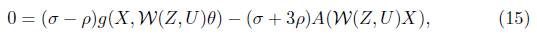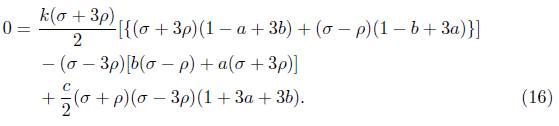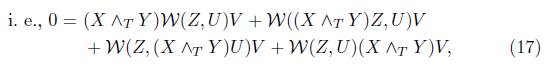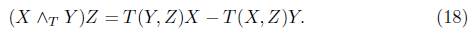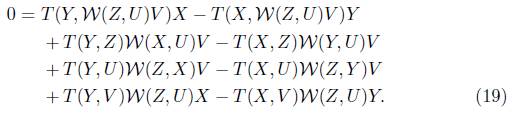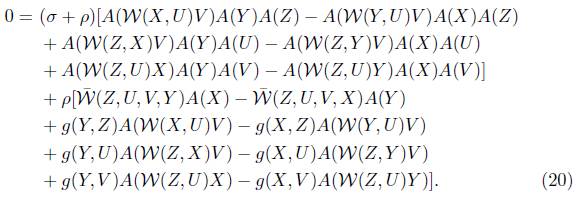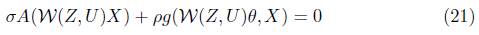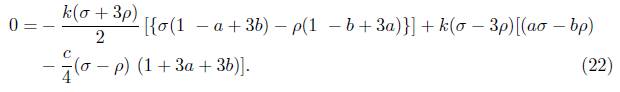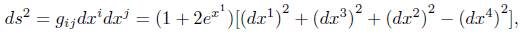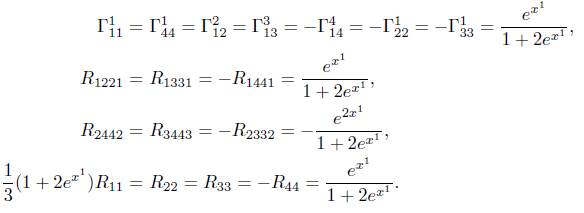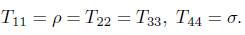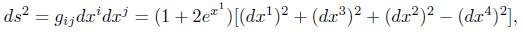Inglês (pdf)
Artigo em XML
Referências do artigo
Tradução automática
Enviar este artigo por email
Citado por SciELO 
Citado por Google 
Similares em
SciELO 
Similares em Google 
Permalink
1. Introduction
Recently, in tune with Yano and Sawaki [16], Baishya and Roy Chowdhury [4] introduced and studied quasi-conformal curvature tensors in the frame of N(k, μ)-manifolds. The generalized quasi-conformal curvature tensor is defined for n dimensional manifolds as
for all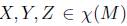 
, the set of all vector fields of the manifold M, where scalars a, b, c are real constants. The beauty of such curvature tensors lies on the fact that it has the flavour of
(i) Riemannian curvature tensors R if the scalar triple (a, b, c) = (0, 0,0),
(ii) Conformal curvature tensors C [9] if
,(iii) Conharmonic curvature tensors
[10] if 
,(iv) Concircular curvature tensors E [15, p. 84] if (a, b, c) = (0,0,1),
(v) Projective curvature tensors P [15, p. 84] if
,(vi) m-projective curvature tensors H [12] if
.
Note that (1) can also be written as
The space-time under various curvature restrictions is a subject of vast literature, e.g., [1,5,7,8] and the references there in.
In analogy with [14], an energy-momentum tensor T of type (0, 2) is said to be semi-symmetric type if
holds where W( X, Y) acts on T as a derivation.
The paper is structured as follows. Section 2 is concerned with general relativistic perfect fluid space-time (briefly GRPFS) obeying Einstein's equation with W(X, Y) · T = 0. It is observed that a fluid of such space-time always behaves as phantom barrier for each of the restrictions E( X, Y) · T = 0 and H( X, Y) · T = 0 whereas the same behaves either as a phantom barrier or quintessence barrier for each of the restrictions R(X, Y) · T = 0 and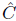 
(X, Y) · T = 0. A detailed study of GRPFS obeying Einstein's equation admitting ((
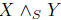) · W) = 0 and (
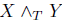) = 0, where the endomorphism is defined as (
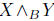)Z = B(Y, Z )X - B(X, Z )Y, has been carried out in Section 3 and 4 respectively, with similar types of results as in Section 2. Finally, we give an example in Section 5 of a fluid whose character is phantom barrier.
2. GRPFS with semi-symmetric type energy momentum tensors
Einstein's equation can be written as
where k is the gravitational constant and r is the scalar curvature. Let (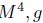
) be a GRPFS with (3). Now (3) implies that
In view of (4) and (5), we have
In consequence of the above, we have the following:
Proposition 2.1. A general relativistic space-time with a semi-symmetric type energy-momentum tensor is Ricci semi-symmetric type and vice-versa.
By [5, Theorem 1, p 1029], we can easily bring out the following:
Proposition 2.2. A general relativistic space-time with a covariant constant energy-momentum tensor is Ricci semi-symmetric type.
By virtue of a result of Aikawa and Matsuyama [2] if a tensor field L is recurrent or birecurrent, then R(X, Y) · L = 0. Hence we have the following:
Theorem 2.3. A general relativistic space-time with a recurrent or birecurrent energy-momentum tensor is always Ricci semi-symmetric type.
Next we consider a perfect fluid space-time whose energy-momentum tensor is semi-symmetric type. An energy-momentum tensor is said to describe a perfect fluid [11] if
where σ is the energy density, ρ is the isotropic pressure of the fluid and A is a non-zero 1-form such that g(X, θ) = A(X) for all X, θ being the velocity vector field of the fluid which is a time-like vector that is,
By virtue of (4) and (6), we get
In view of (2) and (7), we have
As consequences of (5) and (6), it follows that
which yields
for V = θ which in turn on contraction gives
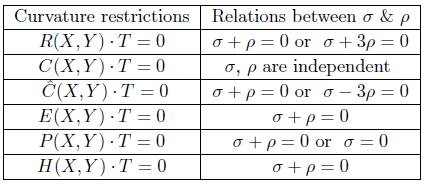
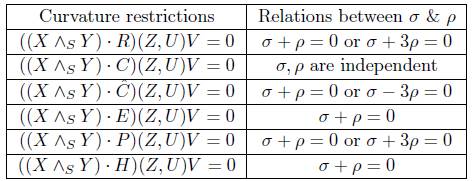
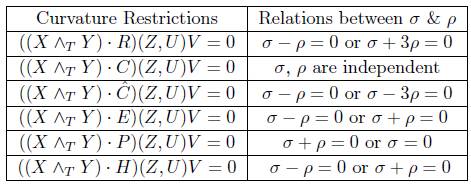
From (11), one can easily bring out the following table by substituting the triple (a, b, c) by (0, 0, 0),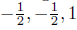 
, etc.
Now σ + ρ = 0 means that the fluid behaves as a cosmological constant [13]. This is also termed as phantom barrier [6]. In cosmology, a choice σ = -ρ leads to a rapid expansion of the space-time which is now termed as inflation. Also σ + 3ρ = 0 or (σ - 3ρ = 0) is known as the quintessence barrier. Here the strong energy condition begins to be violated. The present observations indicate that our universe is in quintessence era [3]. Thus from the above discussion we can state the following:
Theorem 2.4. Let (M4, g) be a GRPFS obeying Einstein's equation admitting C(X, Y) · T = 0. Then the density of the matter and pressure are independent.
Theorem 2.5. The behavior of fluids in GRPFS obeying Einstein's equation is always phantom barrier for each of the restrictions E(X, Y) · T = 0 and H(X, Y) · T = 0.
Theorem 2.6. The behavior of a fluid in GRPFS obeying Einstein's equation is either phantom barrier or quintessence barrier for each of the restrictions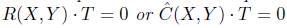 
.
3. GRPFS satisfying 
Let us consider a perfect fluid space-time satisfying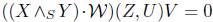 
,
where the endomorphism (X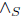 
Y)Z is defined as
In view of (13), (12) becomes
Replacing Y and V by θ, we get
which on contraction yields
Consequently, from (16) one can easily bring out the following:
Theorem 3.1.
The behavior of fluids in GRPFS obeying Einstein's equation is always phantom barrier for each of the restrictions (X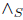
Y) · E = 0 and (X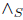Y) · H = 0.
Theorem 3.2.
The behavior of fluids in GRPFS obeying Einstein's equation is either phantom barrier or quintessence barrier for each of the restrictions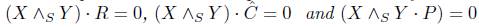
.
4. The Perfect fluid space-time satisfying ((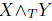
) · W) = 0
Let us consider the perfect fluid space-time satisfying ((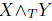) · W) = 0,
where the endomorphism (X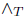 
Y)Z is defined as
In consequence of (18), (17) becomes
In view of (6) and (19), we have
Replacing Y and V by θ in (20), we get
which on contraction gives
From the above one can easily bring out the following:
Theorem 4.1.
The behavior of fluids in GRPFS obeying Einstein's equation is always phantom barrier for each of the restrictions (X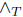
Y) · E = 0 (for σ ≠ ρ), (X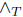Y) · H = 0 for σ ≠ ρ and (X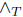Y) · P = 0 for σ ≠ 0.
Theorem 4.2.
The behavior of fluids in GRPFS obeying Einstein's equation is always quintessence barrier for each of the restrictions (X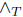Y) · R = 0 for σ ≠ ρ and (X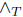Y) ·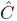 
= 0 for σ ≠ ρ.
5. An example of a fluid whose character is phantom barrier
Example 5.1. Let (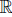
4,g) be a 4-dimensional Lorentzian space endowed with the Lorentzian metric g given by
(i, j = 1, 2, 3,4). The only non-vanishing components of the Christoffel symbols and the Ricci tensors (up to symmetry) are
The scalar curvature r of the resulting space (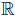
4, g) is 
Now using the above results, we may have
Assuming the associate vector field θ in the direction of x4, we have
As consequences of the above relations, we can easily bring out the following:
This leads to the following
Theorem 5.2. Let (
4, g) be a 4-dimensional Lorentzian space endowed with the Lorentzian metric g given by
(i, j = 1, 2, 3, 4). Then the behavior of fluids in general relativistic perfect fluid space obeying Einstein's equation is always phantom barrier for each of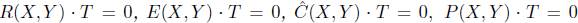 
and
