Introducción
México se ha consolidado como el quinto país productor a nivel mundial de naranja, con un volumen promedio de 4,2 millones de toneladas, las cuales se comercializaron tanto en el mercado nacional como internacional (Secretaría de Agricultura, Ganadería, Desarrollo Rural, Pesca y Alimentación 2017). Además, se considera el quinto país a nivel mundial como productor de mango, en donde destacan por su producción, los siguientes estados: Guerrero con 358 mil 235 toneladas, Sinaloa con 334 mil 239, Nayarit tiene 312 mil 39, Chiapas 237 mil 530, Oaxaca 158 mil 847 y Michoacán 146 mil 767 toneladas. Globalmente, es el quinto productor de guayaba, los meses de mayor disponibilidad de esta fruta son de octubre a noviembre, con aproximadamente el 41 % de la producción nacional (Secretaría de Agricultura, Ganadería, Desarrollo Rural, Pesca y Alimentación 2017).
Las especies del género Anastrepha spp. están consideradas como las plagas principales en cultivos frutales al afectar directamente los frutos. El manejo de esta plaga se realiza con la aplicación de varias estrategias de control bajo un enfoque integral (Reyes et al. 2000). Estas plagas producen un daño directo cuando la hembra ovoposita en la pulpa de los frutos (Aluja 1994). Además, el daño provocado por la ovipostura favorece la entrada de hongos y bacterias que ocasionan la descomposición de la pulpa, aunado a las galerías de las larvas durante su alimentación. Todo esto produce una maduración precoz, caída del fruto y pérdida de cosecha (Curti-Díaz et al. 1998).
Las especies de Anastrepha de mayor importancia son: A. ludens (Loew, 1873), A. obliqua (Macquart, 1835), A. serpentina (Wiedemann, 1830) y A. striata (Schiner, 1868) de las cuales se desconoce su distribución espacial, necesaria para dirigir las medidas de control sobre áreas específicas de infestación. Por lo tanto, este trabajo tuvo por objetivo determinar la distribución espacial de las poblaciones de mosca mexicana de la fruta en cultivos de ciruela mexicana, naranja, zapote, guayaba y mango, mediante la aplicación de técnicas de estadística espacial que condujeron a la generación de mapas por medio del “krigeado”.
Materiales y métodos
El estudio se llevó a cabo de marzo a septiembre del año 2018 en el oriente de Michoacán, (México) debido a que es la principal zona productora de guayaba (Psidium guajava L.) y donde en las áreas marginales se encuentran otros hospederos como zapote (Diospyros digyna Jacq.), ciruela mexicana (Spondias purpurea L.), naranja (Citrus × sinensis Osbeck), mango (Mangifera indica L.). Cada uno de estos cultivos fueron muestreados. Esta región comprende los municipios de Zitácuaro, Benito Juárez, Jungapeo, Tuxpan y Ciudad Hidalgo. Para llevar a cabo el muestreo se colocaron 819 trampas tipo Jackson de manera aleatoria, cubriendo una superficie aproximada de 2.000 hectáreas colocando una trampa por cultivo, se realizó un solo muestreo utilizando como atrayente alcohol - metanol; las trampas utilizadas fueron facilitadas por la junta local de sanidad vegetal del oriente de Michoacán. La verificación de las trampas se realizó cada 15 días, hasta cubrir el área de estudio.
Análisis geoestadístico
Con el valor promedio de captura mensual de adultos con el programa variowin 2,2 (Software for spatial data analysis en 2D. New York, EE. UU.) se obtuvo el semivariograma experimental calculado con la siguiente expresión (Journel y Huijbregts 1978; Isaaks y Srivastava 1988):
donde: γ * (h) es el valor experimental del semivariograma para el intervalo de distancia h; N(h) es el número de pares de puntos muestrales separados por el intervalo de distancia h; z(x i ) es el valor de la variable de interés en el punto muestra x i y z (x i + h) es el valor de la variable de interés en el punto muestral x i + h.
Estimación de los parámetros del modelo de semivariograma
Una vez obtenido el semivariograma experimental, se realizó su ajuste al semivariograma teórico (esférico, exponencial, gaussiano, etc.) Englund y Sparks (1988) utilizando el programa Variowin versión 2,2.
Validación del modelo teórico
Se siguió un procedimiento de validación cruzada, en el cual los parámetros del modelo Co (efecto de pepita), C + Co (meseta) y a (rango o alcance) fueron ajustados de forma interactiva (prueba y error) hasta obtener los valores de los estadísticos:
a. Media de los errores de estimación (MEE):
dónde: z * (x i ) es el valor estimado de la variable de interés en el punto xi; z (xi) es el valor medido de la variable de interés en el punto x i y n es el número de puntos muestréales considerado en la interpolación.
El MEE no debe ser significativamente distinto de 0 (test t), en cuyo caso, indicaría que el modelo de semivariograma permite el cálculo de las estimaciones no sesgadas.
b. Error cuadrático medio (ECM):
Un modelo de semivariograma se considera adecuado si, como regla práctica, el ECM es menor que la varianza de los valores muéstrales (Hevesi et al. 1992).
c. Error cuadrático medio adimensional (ECMA):
donde: σk es la desviación standar del error esperado en la estimación con el “krigeado”.
La validez del modelo se satisface si ECMA está comprendido entre los valores 1 ± 2 (2 / N)0.5.
Nivel de dependencia espacial
La determinación del grado de relación entre los datos o nivel de dependencia espacial se obtuvo al dividir el efecto pepita entre la meseta expresando en el resultado en porcentaje. Si el resultado es menor de 25 % el nivel de dependencia espacial es alta, si el rango está entre 26 y 75 % el nivel es moderado y si es mayor del 76 % el nivel de dependencia es bajo (Cambardella et al. 1994).
Elaboración de mapas
Para la estimación insesgada de valores asociados a puntos que no fueron muestreados se realizó la interpolación de valores a través del “krigeado” ordinario. Las estimaciones obtenidas fueron representadas en forma de mapa, mediante el uso del programa Surfer 9, Surface 266 Mapping System, (Golden Software Inc. 2021).
Resultados
En las 2.000 ha muestreadas, la especie de mosca que registró mayor captura fue A. ludens seguida por A. striata y por A. obliqua. La distribución espacial que se obtuvo en las poblaciones de las tres especies de moscas fue de tipo agregada, los modelos a los que se adecuaron a los semivariogramas fueron esféricos y gaussianos (Tabla 1).
Tabla 1 Parámetros (efecto pepita, meseta y rango) de los modelos ajustados a los semivariogramas de las poblaciones de mosca de la fruta (Anastrepha spp.) en los cultivos de ciruela mexicana, guayaba, mango, naranja, zapote, en el año 2018. Meseta: valor asintótico de cada semivariograma. Rango: distancia máxima hasta donde los datos tienen relación espacial.
| Cultivo | Modelo | Pepita | Meseta | Rango | Pepita/ Meseta | Nivel de dependencia espacial | Coeficiente de Curtosis |
|---|---|---|---|---|---|---|---|
| Ciruela | |||||||
| Anastrepha ludens | Gaussian | 0 | 9750 | 0,0228 | 0 | Alta | 1,21 |
| Anastrepha striata | Esférico | 0 | 16000 | 0,0840 | 0 | Alta | 2,05 |
| Guayaba | |||||||
| Anastrepha ludens | Esférico | 0 | 4554 | 0,2160 | 0 | Alta | 1,34 |
| Anastrepha obliqua | Esférico | 0 | 4818 | 0,0299 | 0 | Alta | 1,29 |
| Anastrepha. striata | Esférico | 0 | 5412 | 0,0616 | 0 | Alta | 2,46 |
| Mango | |||||||
| Anastrepha ludens | Esférico | 0 | 27000 | 1,1250 | 0 | Alta | 2,05 |
| Anastrepha obliqua | Esférico | 0 | 2160 | 0,0712 | 0 | Alta | 1,93 |
| Anastrepha striata | Esférico | 0 | 11610 | 0,2799 | 0 | Alta | 1,03 |
| Naranja | |||||||
| Anastrepha ludens | Gaussian | 0 | 13749 | 0,2339 | 0 | Alta | 1,66 |
| Anastrepha obliqua | Gaussian | 0 | 10250 | 0,0280 | 0 | Alta | 2,24 |
| Anastrepha striata | Gaussian | 0 | 3213 | 0,0464 | 0 | Alta | 1,80 |
| Zapote | |||||||
| Anastrepha ludens | Espacial | 0 | 10500 | 0,328 | 0 | Alta | 2,29 |
| Anastrepha obliqua | Gaussian | 0 | 15750 | 0,096 | 0 | Alta | 2,17 |
| Anastrepha striata | Gaussian | 0 | 14749 | 0,136 | 0 | Alta | 1,73 |
Para todos los modelos ajustados se observó un efecto pepita igual a cero, este hecho indicó que la escala de muestreo utilizada fue la correcta y el error de muestreo fue de 0. El rango indica la distancia máxima hasta donde los datos muestreados tienen relación espacial entre sí, siendo en este caso bastante amplio. El valor de la meseta indica el valor asintótico de cada semivariograma. Todos los muestreos presentaron un alto nivel de dependencia espacial para cada uno de los mapas. Los modelos de la distribución espacial de las tres especies de moscas de la fruta fueron capturados y se validaron con los parámetros estadísticos al ubicarse dentro del rango permisible (Tabla 2).
Tabla 2 Valores de los estadísticos de la validación cruzada de los semivariogramas obtenidos en los muestreos de Anastrepha spp.: media de los errores de estimación (MEE), error cuadrado medio (ECM) y error cuadrático medio adimensional (ECMA).
| Cultivo | Muestreos | Media muestral | Varianza muestral | MEE* | Varianza de los errores | ECM | ECMA |
|---|---|---|---|---|---|---|---|
| Ciruela | Anastrepha ludens | 0,169 | 0,350 | 0,11ns | 0,123 | 0,10 | 1,13 |
| Anastrepha striata | 0,119 | 0,210 | 0,14ns | 0,156 | 0,12 | 1,10 | |
| Guayaba | Anastrepha ludens | 0,162 | 0,304 | 0,10ns | 0,219 | 0,14 | 1,06 |
| Anastrepha striata | 0,063 | 0,071 | 0,12ns | 0,030 | 0,11 | 1,11 | |
| Anastrepha obliqua | 0,024 | 0,041 | 0,13ns | 0,026 | 0,09 | 1,09 | |
| Zapote | Anastrepha ludens | 0,382 | 0,365 | 0,09ns | 0,189 | 0,11 | 1,12 |
| Anastrepha striata | 0,114 | 0,163 | 0,10ns | 0,111 | 0,14 | 1,13 | |
| Anastrepha obliqua | 0,059 | 0,118 | 0,14ns | 0,015 | 0,08 | 1,08 | |
| Naranja | Anastrepha ludens | 0,161 | 0,269 | 0,08ns | 0,148 | 0,06 | 1,14 |
| Anastrepha striata | 0,081 | 0,075 | 0,10ns | 0,032 | 0,11 | 1,10 | |
| Anastrepha obliqua | 0,048 | 0,047 | 0,07ns | 0,016 | 0,10 | 1,05 | |
| Mango | Anastrepha ludens | 0,361 | 1,496 | 0,11ns | 1,105 | 0,13 | 1,12 |
| Anastrepha striata | 0,153 | 0,3565 | 0,13ns | 0,271 | 0,08 | 1,14 | |
| Anastrepha obliqua | 0,076 | 0,080 | 0,09ns | 0,056 | 0,12 | 1,09 |
En los mapas del área infestada (Fig. 1), en el caso del cultivo de ciruela se presentaron adultos de A. ludens y A. striata, siendo las poblaciones de la primera especie las de mayor abundancia. No hubo captura de A. obliqua en dichos cultivos. En los cultivos de guayaba se capturaron adultos de las tres especies, donde A. ludens y A. striata se situaron en la parte izquierda central del mapa y A. obliqua en el centro. En los cultivos de mango también se capturaron las tres especies pero con A. ludens la de mayor abundancia, ubicada en el centro del mapa con tendencia a crecer hacia el lado izquierdo; sin embargo, A. obliqua se situó en la parte inferior del mapa y A. striata se ubicó en el centro con tendencia a ser más abundante en la parte izquierda. En los cultivos de naranja A. ludens y A. obliqua se ubicaron en el centro del mapa, tendiendo a ser más abundantes en la parte superior derecha, mientras que A. striata se ubicó en el centro y en la parte inferior izquierda y derecha del mapa. Para el cultivo de zapote A. ludens se ubicó en la parte central del mapa, mientras que A. obliqua en la parte inferior izquierda, en tanto que A. striata se encuentra en la parte inferior derecha (Fig. 1).
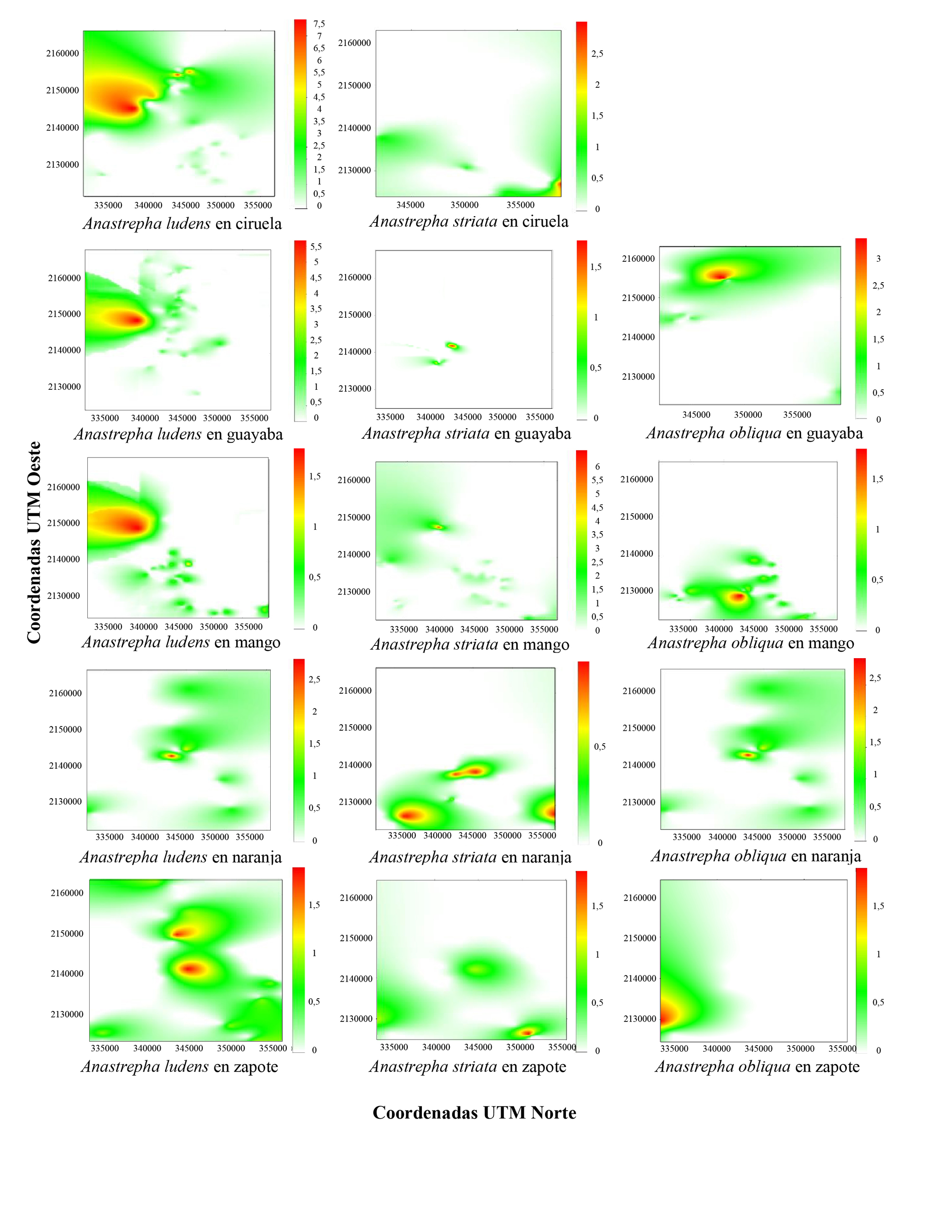
Figura 1 Mapas de distribución espacial de las moscas de la fruta Anastrepha ludens, A. oblicua y A. striata, en cultivos de frutales en el oriente de Michoacán, México, 2018.
En los cultivos se observó una infestación que fluctuó de 31 % hasta el 88 %. Cabe destacar que en ciruela mexicana no se capturaron adultos de A. obliqua pero si en cultivos de guayaba en los que alcanzó el 88 % de infestación (Tabla 3).
Tabla 3 Superficie infestada de mosca de la fruta (Anastrepha spp.) dentro de las áreas de estudio, Michoacán, México en 2018.
| Cultivo y especie de mosca | % de infestación en los cultivos |
|---|---|
| Ciruela, Anastrepha ludens | 42 |
| Ciruela, Anastrepha striata | 45 |
| Ciruela, Anastrepha obliqua | 0 |
| Guayaba, Anastrepha ludens | 38 |
| Guayaba, Anastrepha obliqua | 88 |
| Guayaba, Anastrepha striata | 46 |
| Mango, Anastrepha ludens | 48 |
| Mango, Anastrepha obliqua | 28 |
| Mango, Anastrepha strata | 36 |
| Naranja, Anastrepha ludens | 39 |
| Naranja, Anastrepha obliqua | 39 |
| Naranja, Anastrepha striata | 31 |
| Zapote, Anastrepha ludens | 50 |
| Zapote, Anastrepha obliqua | 28 |
| Zapote, Anastrepha striata | 35 |
Discusión
En la distribución de las especies de moscas de la fruta se encontró una mayor captura de A. ludens en comparación con A. obliqua y A. striata, y fue mayor en las zonas con temperaturas superiores a los 25 °C.
Las poblaciones de las tres especies de mosca de la fruta disminuyeron en la temporada de otoño-invierno y para los meses más cálidos (primavera - verano) esto está relacionado directamente con la temperatura que influye en su ciclo biológico (Comité Estatal de Sanidad Vegetal de Veracruz 2019).
En el cultivo de ciruela no se encontró infestación de A. obliqua, contrario a lo reportado por Marín Patiño (2002) pero confirma que los frutos de S. mombin es un hospedante de A. obliqua.
La aplicación de las técnicas para modelizar la distribución espacial de insectos es una herramienta muy eficaz para determinar la distribución espacial de diversas especies de insectos plaga en diferentes cultivos. En estudios como el de Sciarretta et al. (2008) se ha reportado una distribución agregada con ajuste al modelo esférico en Lobesia botrana en plantaciones de uva. Así mismo Rivera-Martínez et al. (2017)determinaron la distribución espacial agregada en las poblaciones de adultos de Bactericera cockerelli Sulc., en el cultivo de tomate de cáscara (Physalis ixocarpa Brot.), También Jiménez et al. (2013) en poblaciones de trips en tomate de cáscara encontraron que exhiben una distribución agregada en varios centros de agregación y sus semivariogramas se ajustaron a los modelos esférico y gaussiano. Además, Bressan et al. (2010) determinaron la distribución espacial de Pentastiridius leporinus L. en el cultivo de trigo; Ramírez Dávila et al. (2011) mencionan que la distribución de Bactericera cockerelli en el cultivo de papa fue de tipo agregada.
Cuando los datos de la distribución espacial de un organismo son analizados con estadística clásica los resultados pueden variar, la diferencia está en que los modelos geoestadísticos proporcionan una medida más directa de la dependencia espacial, ya que consideran la naturaleza bidimensional de la distribución de los organismos a través de su exacta localización espacial y es independiente de la relación entre la media y la varianza (Samper y Carrera Ramírez 1996). Además, la geoestadística permite elaborar mapas de densidad de la distribución espacial de un organismo (Rossi et al. 1992; Ribes et al. 1998).
Moral García (2004) al utilizar la geoestadística para estudiar la distribución espacial del lepidóptero Helicoverpa armigera Hübner, en una parcela de tomate, con el empleo de la función variograma, obtuvo representaciones gráficas diarias de dichas distribuciones. Estos mapas se basan en la técnica de estimación geoestadística conocida como “krigeado”, particularmente el ordinario en bloques. Contreras-Rendón et al. (2016) en un estudio de la distribución espacial de Candidatus liberibacter solanacearum y de su vector Bactericera cockerelli Sulc en papa, obtuvieron mapas de densidad de B. cockerelli tanto en huevos, ninfas y adultos, usando el krigeado. En aguacate, Acosta-Guadarrama et al. (2017) mencionan el uso de mapas de distribución espacial de trips en diferentes épocas del año, para planear diversas estrategias de control (cultural, biológico o químico).
El comportamiento espacial de las poblaciones de las tres especies de mosca de la fruta de forma agregada en las parcelas de los diferentes frutales del oriente de Michoacán, permite sugerir que se pueden manejar y, por lo tanto, reducirlas aplicando y dirigiendo medidas de control hacia los centros de agregación o puntos específicos en los que se encuentra la plaga, evitando aplicaciones generalizadas o de cobertura total, con un ahorro en los insumos, visualizando los focos de infestación a través de los mapas generados. Lo anterior concuerda con Tannure et al. (2013) quienes propusieron un manejo para controlar al pulgón del algodonero Aphis gossypii para las etapas temprana e intermedia del cultivo de algodón.
De acuerdo con los valores de cero que se registraron en el efecto pepita en todos los modelos ajustados, se puede afirmar que la escala de muestreo utilizada fue adecuada y el error de muestreo fue mínimo (Oliver y Webster 1991), esto sugiere que los modelos ajustados tienen un 98 % de confiabilidad. Este hecho indicó que más del 90 % de la variación total es debida a la dependencia espacial en la escala de muestreo utilizada; es decir, que más del 90 % de la variación de la distribución de las poblaciones de mosca de la fruta se explica por la estructura espacial establecida con los semivariogramas (Liebhold y Sharov 1998). Valores de pepita iguales fueron obtenidos por Ramírez Dávila et al. (2011) en un estudio de la distribución espacial de Bactericera cockerelli en papa y por Solares Alonso et al. (2011) en la distribución espacial de trips en cultivos de aguacate.
El ajuste al modelo esférico indicó que dentro del área de muestreo hay puntos en los que la plaga tiene mayor abundancia con respecto a otros puntos, es decir que la infestación de la plaga que avanza a partir de una zona puntual, la infestación aumenta drásticamente en primavera. La distribución ajustada al modelo gaussiano reflejo que la agregación se expresó de forma continua dentro del área de muestreo. Estos puntos de agregación registraron un crecimiento rápido cerca de su origen pero decrecen conforme aumenta la distancia, esto es factible dado el comportamiento de las especies de mosca de la fruta, los focos de infestación se observan en los mapas obtenidos. Moral García (2006)al realizar la distribución espacial de H. armigera y sus variogramas teóricos, encontró que se ajustaron a modelos esféricos o exponenciales. Contreras-Rendón et al. (2016) encontraron que los semivariogramas para huevos y ninfas de B. cockerelli se ajustaron al modelo esférico, lo que indicó la agregación de la plaga en ciertas zonas de la parcela.
El alto nivel de dependencia espacial que resultó de dividir el efecto pepita entre la meseta fue menor a 25 % para todos los semivariogramas con una alta dependencia espacial. Esto sugiere que las poblaciones de moscas de la fruta dependen entre sí y que el nivel de agregación es alto (Rossi et al. 1992). Esquivel Higuera y Jasso García (2014) en un estudio de la distribución espacial de Spodoptera exigua demostraron que hay una estructura espacial agregada, con un nivel de dependencia espacial alto para las seis localidades en estudio.
En los mapas de densidad que fueron generados se observan los centros de agregación que presentó el insecto dentro de la parcela, lo que indica que el control de la plaga se puede hacer con mayor precisión (Weisz et al. 1996; Ribes et al. 1998; Moral García 2004; Rong et al. 2006; Esquivel Higuera y Jasso García 2014). Si se mejoran las estrategias de control también se reduce la presión de selección y se puede retrasar el desarrollo de resistencia en los insectos a los plaguicidas debido a la creación de refugios temporales dinámicos, al no tratar toda la superficie del cultivo (Moral et al. 2011). Con estas acciones se evitará una mayor distribución de las tres especies de mosca de la fruta y que causen mayores daños económicos.
Considerando la estructura de los mapas, las áreas de infestación de las especies de mosca de la fruta que se distribuyeron de un 31 % a un 88 % de la parcela tienen similitud a lo reportado por Esquivel Higuera y Jasso García (2014) para la distribución espacial de S. exigua en maíz con un porcentaje máximo de 94 %. Así mismo, Jiménez et al. (2013) y Arce-Flores et al. (2014) reportaron que las poblaciones de Frankliniella occidentalis no se distribuyen en la totalidad de las parcelas en tomate de cáscara y de nardo, respectivamente. Todo lo anterior confirma que la infestación de los insectos no se presenta uniforme dentro de los cultivos.
Con el uso de los mapas generados en este estudio se pueden sugerir acciones a los productores para llevar a cabo acciones que permitan reducir las poblaciones de los insectos plaga. Entre los métodos a sugerir están, el control biológico en todas sus modalidades, el control cultural, el control físico, el control químico, entre otros. La implementación de los métodos geoestadísticos en el manejo integrado de esta plaga puede ser de gran impacto para los productores, ya que permite conocer con mayor precisión y eficiencia el comportamiento espacial de este insecto. Los mapas elaborados mediante estos métodos de estadística espacial proporcionaran a las autoridades competentes y al personal especializado, un componente novedoso y de gran ayuda para el desarrollo de nuevos y más pertinentes programas de manejo integrado de este problema fitosanitario, que sin duda alguna, impactará positivamente en la producción frutícola de la región.















