INVESTIGACIONES

La separación en regresión logística, una solución y aplicación

The problem of separation in logistic regression, a solution and an application

Juan C. Correa M¹; Marisol Valencia C².

¹ PhD. en Estadística, University of Kentucky. Docente, Universidad Nacional de Colombia, Medellín, Colombia. Correo electrónico: jccorrea@unal.edu.co, jccorreamorales@gmail.com

² Msc en Estadística, Universidad Nacional de Colombia, docente, Universidad Pontifica Bolivariana, Medellín, Colombia. Correo electrónico: solmarival@hotmail.com

RESUMEN

La regresión logística es una de las técnicas estadísticas más aplicadas cuando se busca explicar el comportamiento probabilístico de algún fenómeno. Un problema que aparece con frecuencia en estos modelos es la separación en los datos, mostrando los grupos de éxitos separados de los fracasos, lo que impide hallar los estimadores de máxima verosimilitud.
OBJETIVO: Presentar una revisión y solución del problema, comparando con otras existentes.
METODOLOGIA: Simulación del modelo logístico y estimación del sesgo de los parámetros, usando la solución propuesta con el método clásico. Bayesiano y observaciones ficticias y con el método de Firth.
RESULTADOS: Los sesgos encontrados son menores al generar el par de observaciones ficticias con el método Bayesiano. Se muestra un ejemplo sobre la edad de la menarquia.
DISCUSION: Se aporta una solución adecuada al problema de la separación usando simulación en un esquema de modelo logístico sencillo. Conclusiones: la generación de observaciones ficticias se recomienda dentro de la región de separación y el mejor método de solución está basado en la teoría bayesiana, donde se logra una convergencia en los parámetros del modelo logístico.

Palabras Clave: modelo logístico, estimación de máxima verosimilitud, menarquia.

ABSTRACT

Logistic regression is one of the most used statistical techniques for explaining the probabilistic behavior of a given phenomenon. Data separation is a frequent problem in this model, as successes appear separated from failures and make it impossible to find the maximum likelihood estimators. Objective: to present a revision and a solution to the problem, and to compare it with other solutions.
METHODOLOGY: a simulation of the logistic model and an estimation of the parameters' bias using the proposed classical and Bayesian solution with fictitious observations, as well as the Firth method. Results: the bias found is lower when the pair of fictitious observations are generated using the Bayesian method. An example about the age at which menarche occurs is presented.
DISCUSSION: an appropriate solution to the problem of separation is provided using a simulation in a simple logistic model.
CONCLUSIONS: the generation of fictitious observations within the separation region is recommended, and the best solution method is based on Bayesian theory, which achieves convergence of the parameters of the logistic model.

Key words: logistic model, maximum likelihood estimation, menarche.

Introducción

La regresión logística es una de las técnicas que se ha convertido en una herramienta de uso permanente entre investigadores de la salud. Un problema que aparece con frecuencia en los datos usados para estos modelos, es el de la separación que trae como consecuencia la no existencia de los estimadores de máxima verosimilitud. Muchas veces los investigadores no son conscientes de la existencia de este problema, ya que no todo software estadístico advierte sobre la presencia de separación en el conjunto de datos y entregan información parcial sobre el proceso de convergencia y presentan resultados no adecuados de los estimadores.

Este problema es generado por una estructura en los datos que se conoce como separación completa [1-3, 4, 8]. Aun así, hay autores [6] que sostienen que cuando los parámetros no convergen, la predicción es perfecta. La separación se puede definir como una división completa de los dos "grupos" de puntos asociados a los valores que toma la variable respuesta (en estos conjuntos de datos, la codificación general es 0 y 1). La principal consecuencia de la separación es la no existencia de los estimadores de máxima verosimilitud, por lo tanto, cuando los usuarios se enfrentan a este problema, no logran una solución y no pueden realizar inferencias, o las hacen incorrectamente [1].

Al respecto existen propuestas, como la de Christmann y Rousseeuw, que consiste en dar una solución basada en un modelo de regresión logístico oculto, donde las respuestas no observadas se consideran como latentes [2]. King y Ryan han comparado el método de regresión logística exacto y el método de máxima verosimilitud cuando se enfrentan al problema de la separación, analizando los estimadores de máxima verosimilitud encontrados con sobreposición (a diferentes niveles), calculan los valores p y los intervalos de confianza, y analizan la función de log- verosimilitud, encontrando resultados más pobres para este método cuando hay un acercamiento a la separación [4].

Asimismo, Heinze y Shemper desarrollaron un procedimiento basado en una modificación de la función score en el procedimiento de estimación de la regresión logística [10], originalmente propuesta por Firth para reducir el sesgo de los estimadores de máxima verosimilitud [11]. Heinze y Shemper afirman que la separación depende del tamaño de muestra, el número de factores dicotómicos, el total de éxitos y fracasos [10].

Se presentan dos posibles soluciones al problema de la separación, con las que se aproximan los estimadores de máxima verosimilitud, mediante el uso de seudo-observaciones ficticias, comparando con la solución dada por Firth [11].

El Problema de la separación

Suponga que el conjunto de datos corresponde a n puntos p-dimensionales, y cada punto es de la forma: (x_i1, ... , x_i(p - 1), y_i) con i=1,...n donde yi es el valor de la variable respuesta de interés (codificada como 0 ó 1), y x_i1, ... , x_i(p - 1) es el conjunto de las p-1 variables explicatorias. En el caso más simple, p = 2, los n puntos corresponden al sistema de coordenadas XY: (x_i1, y_i).

La existencia de los estimadores de máxima verosimilitud está condicionada por el comportamiento de la variable dicótoma en el grupo de datos. En [8] se presentan las condiciones para la existencia de los estimadores de máxima verosimilitud. Algunos autores [1] examinan la maximización de la función de log-verosimilitud considerando las posibles configuraciones de los n puntos muestrales en el espacio de observaciones Rp. Las posibles configuraciones caen esencialmente en 3 categorías mutuamente exclusivas y exhaustivas.

Separación completa, separación cuasicompleta, sobreposición (Overlap)

Existe separación cuando se presenta la división completa de los dos "grupos" de puntos asociados a los valores que toma la variable respuesta (adoptando una codificación general de 0 y 1), uno de los grupos corresponde a todos los puntos de la forma (xi, 0), puntos de la muestra donde no ocurre el evento de interés y el otro corresponde a los puntos muestrales donde ocurre dicho evento, de la forma (xi, 1) [1]. En el caso de una sola variable explicatoria x, la separación se presenta cuando ocurren todos los fracasos en la primera parte del rango de la variable x (R1), y todos los éxitos en la segunda parte de este rango (o viceversa) (R2), sin dar lugar a una sobreposición de ambos rangos, o mezcla de éxitos y fracasos. Sin embargo, existe un tercer rango de x, donde no hay realizaciones de la variable Y, este representa la "región de separación", ya que separa totalmente los éxitos de los fracasos (Rs) (figura 1).

Figura 1. Región de separación en el caso bivariado

En el caso en que ocurren primero éxitos y después fracasos (al tener 1 variable explicatoria), la separación se detecta cuando la sumatoria de los éxitos de todo el rango de X, es igual a la sumatoria de los valores de y en uno de los lados de la región de separación.

La separación cuasicompleta ocurre cuando es posible definir un plano que pasa por la región de separación con éxitos a un lado o sobre este y fracasos al otro o sobre este, sin presentarse convergencia de los estimadores de máxima verosimilitud.

Se dice que un grupo de datos tiene Sobreposición (u Overlap) si no hay una completa separación y no cuasicompleta separación. En este caso sí se presenta convergencia de los estimadores de máxima verosimilitud.

Para el modelo logístico algunos autores [1, 8] muestran que la estimación de máxima verosimilitud del vector de parámetros β existe sí y sólo si los datos presentan sobreposición, esto significa que no existe ninguna recta, plano o región de separación, ya que los 2 valores que toma la variable respuesta (y_i = 0, y_i = 1) se encuentran mezclados o sobrepuestos en todo el rango de valores de x.

Separación completa

Se utilizó un conjunto de datos sobre 907 jóvenes de la ciudad de Medellín, tomados en el año 2004, con edades entre 5,1 y 19,5 años, ejemplo tomado con fin ilustrativo del problema. A las jóvenes se les preguntó si ya habían presentado o no menarquia, siendo este el primer episodio menstrual de la mujer, encontrando los resultados que se ven en la tabla 1.

Tabla 1. Datos de la edad de la menarquia

En la tabla 1 se observa que hasta los 10,3 años ninguna joven había presentado menarquia; entre las edades 10,3 a 14,4 años no hay datos, y después de los 14,5 años, todas habían presentado ya la menarquia. Luego, los datos presentan separación completa y la región de separación va de 10,3 a 14,5 años.

La no convergencia es mostrada por programas estadísticos como el programa R [7], para este conjunto de datos con separación completa como se ve a continuación:

model=glm(MENARQUIA~EDADCAL,family='bi nomial')
Mensajes de aviso perdidos
In glm.fit(x = X, y = Y, weights = weights, start = start, etastart = etastart:
algorithm did not converge

Sin embargo, el programa entrega un conjunto de parámetros aproximados, pero incorrectos, como se ve en la tabla 2.

Tabla 2. Resultado aproximado para los parámetros

Causas de la separación completa

Problemas de diseño

Los problemas de diseño están asociados a una mala planeación del experimento cuando se desconoce el posible comportamiento de la respuesta a analizar. Sin embargo, aún con una buena planeación puede ocurrir el problema. Para ilustrar consideremos el modelo:

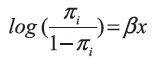
Para valores de x = (-2,-1,1,2) y diferentes valores de b. En cada uno de estos valores de b se fijaron 10 réplicas. Los resultados de una simulación donde se realizaron 1000 repeticiones del diseño anterior, se presentan en la tabla 3.

Tabla 3. Proporción de muestras con separación completa

A medida que aumenta el valor de b, aumenta el porcentaje de casos con separación. Cuando la probabilidad que representa el modelo logístico crece con mayor rapidez, es más fácil encontrar el problema de la separación, ya que el cambio de menor a mayor probabilidad es más notorio.

Rindskopf afirma que la separación no es un problema, ya que cuando éste se presenta en muestras grandes significa que la probabilidad es en un 100% certera, esto es, que con toda seguridad habrá dos grupos discriminados para cualquier otra muestra de esta población, uno de éxitos y otro de fracasos [6]. Sin embargo, si consideramos que el problema se encuentra mal diseñado, y los resultados no tienen en cuenta un rango de la matriz de diseño que en otra muestra puede ocurrir, esta afirmación carece de validez.

Escasez de datos

La escasez de datos se relaciona con tamaños de muestra pequeños, lo cual es frecuente en muchos diseños de datos y si este tamaño de muestra es tan pequeño, que conduce al problema de la separación, no es posible inferir a partir de este conjunto de datos. Es ideal contar con la mayor cantidad de información acerca del problema, por ello es preciso tener una muestra de datos grande.

Soluciones al presentarse separación completa

El comportamiento de los conjuntos de datos en presencia de separación está caracterizado por algunos factores que no siempre son iguales. El número de éxitos puede ser mayor que el de los fracasos, el rango de la matriz de diseño, el de los éxitos y los fracasos, varia en tamaño o longitud. Al existir separación, es posible encontrar mayor incertidumbre al no observar adecuadamente estas características en los datos, decimos entonces que la separación es grave.

Se pueden construir muchos índices de separación, pero la idea básica detrás de cada uno de ellos es dar un indicativo de la gravedad de este problema. A continuación se muestran un indicador propuesto para medir la gravedad de la separación, asumiendo el modelo logístico con una sola variable predictora, así:

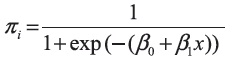
Índice de longitud I_l

Este relaciona el rango de la región de separación (R_s), y el rango completo de la variable predictora x (R).

Este indicador compara la longitud del área donde no hay observaciones con el área completa, o rango completo de la variable explicatoria X. Además se encuentra normalizado, la cercanía a cero indicaría que la separación puede no ser tan grave. La separación es severa cuando I_l → 1, ya que Rs → R, debido a que no es fácil encontrar el verdadero signo de β1, la probabilidad del modelo verdadero puede ser creciente o decreciente, lo cual amerita considerar el total de éxitos y de fracasos, además de la naturaleza del problema.

Metodología

Dos aproximaciones sencillas a la solución de este problema, se describen a continuación.

Simulación de la muestra

Para realizar este proceso se considera el siguiente modelo logístico con una sola variable predictora, mostrado previamente, donde X es la matriz de diseño que contiene los valores de la variable explicativa x, y los yi son los valores de respuesta.

• Se fija una ecuación del modelo logístico, asignando valores a los dos parámetros del modelo: β0 y β1;
• la matriz de diseño X se fija considerando una región donde se debe presentar el punto de inflexión del modelo logístico. Se fija la región de separación a partir de dos valores de x, cercanos a este punto;
• se generan los valores de la variable Y, con distribución Bernoulli (pi), donde pi es la probabilidad del modelo de regresión logística dado inicialmente.

Detección de separación

Sea M el número de muestras con separación se realizan N repeticiones de una muestra aleatoria de la variable respuesta Y. De estas N muestras, M casos tendrán separación completa (M <= N).

A partir de este resultado, es posible determinar la proporción de veces que al simular un conjunto de datos, se presenta separación completa, usando el modelo logístico y la distribución Bernoulli para la variable respuesta Y.

Generación de observaciones ficticias

En un caso donde se presenta separación, de las N muestras generadas, se generan pares de observaciones ficticias en la región de separación. A partir de estos nuevos conjuntos de datos, se calculan los estimadores de máxima verosimilitud (figura 2).

Figura 2. Generación de un par de observaciones ficticias en un conjunto de datos con separación

Dichas observaciones se generaron de dos formas: a) en los extremos de la región de separación; b) dentro de la región de separación, a una distancia de los extremos. En este proceso, se suman a los extremos de la Rs una distancia que equivale a un porcentaje del rango de la región de separación.

En todos los casos, se calculan sesgos relativos absolutos, restando el valor estimado del real y dividiendo por el real.

Análisis Bayesiano

Utilizando técnicas de estadística bayesiana, se muestra una solución y se compara con respecto al anterior método propuesto, analizando ventajas y desventajas de ambos procedimientos.

Función de verosimilitud

Para estimar el modelo logístico, se requieren datos con distribución binomial, así que la verosimilitud tendrá la siguiente naturaleza:

Donde π(x_i) es la probabilidad estimada por medio del modelo logístico dado por:

Luego, la función de verosimilitud quedará así:

Función a Priori para los parámetros del modelo logístico a estimar:

Distribución normal bivariada: β ∼ MN (β₀, Σ) donde se usará la matriz de precisión T=Σ^-1

Luego, la función a posteriori será

ξ(β|datos) ɐ MN (β₀, Σ) * L (β|Y, X)

Así:

Para su desarrollo, se utiliza el algoritmo Metropolis que está programado dentro de la librería MCMCpack, en la función MCMClogit.

Esta función supone una distribución Bernoulli para la variable respuesta y_i, y asume por defecto una distribución normal multivariada a priori para los parámetros a estimar en el modelo (β), donde B₀ es la precisión. Y extrae una muestra de valores de parámetros estimados de (β).

La distribución normal es una distribución a priori propia, lo cual facilita disminuir el impacto sobre la distribución posterior del parámetro de interés y que sea relativamente plana con relación a la verosimilitud. Esto conduce a que los datos tengan dominio en la distribución posterior, y por lo tanto, en todas las inferencias que de ellas se obtengan.

En este trabajo se analizará el escenario bayesiano usando necesario generar sobreposición en el conjunto de datos, y así, esta metodología permite estimar coeficientes y posteriormente el sesgo.

Resultados de la simulación

Simulación de la muestra

Fue fijado el siguiente modelo logístico.

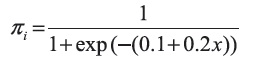
Con este modelo se establece una región de separación según la curva de inflexión, y se eligen los niveles de x que se observan en la tabla 4.

Tabla 4. Matriz de diseño para el conjunto de datos con separación

Detección de Separación

Se generaron 1000 repeticiones de una muestra aleatoria de Y, considerando que Y es una variable aleatoria con distribución Bernoulli (p_i), la probabilidad pi es la probabilidad del modelo dado, usando en el conjunto de valores de x mostrado.

Las frecuencias de casos con separación encontrados se muestran en la tabla 5. Para la simulación de probabilidades del modelo logístico, se fijó el mismo valor de β0 (0.1) y se variaron los de β1 como aparece en dicha tabla, estas se usaron para generar los datos de respuesta dicótomos. El tamaño de muestra (el total de datos) también fue variado, y se generan 1000 muestras en cada caso, contando las frecuencias donde hubo separación completa.

Tabla 5. Frecuencias de casos con separación

Antes de generar los pares de observaciones ficticias, se fijaron otros valores de b₁ cercanos al modelo previamente establecido, encontrando que la frecuencia de muestras con separación aumenta cuando el valor fijado para b₁ aumenta, cuando la R_s es fija. Adicionalmente, la proporción de casos con separación es menor al aumentar el tamaño muestral de los datos (con b₁>0) (tabla 5).

La tabla 6 presenta las estimaciones de parámetros: usando los 3 métodos: el de Firth, con el paquete logistf de R, el método bayesiano usando la función MCMClogit, agregando datos ficticios a un 28% de la región de separación y el clásico usando glm, con el mismo par de ficticias mostrando el sesgo encontrado en cada caso.

Para todas las soluciones probadas, la simulación de variable respuesta parte de los valores: β_o =0,1 y β₁ =0,2.

Tabla 6. Estimaciones de parámetros

Lo anterior sugiere que con pocas observaciones ficticias es posible generar la solución al modelo planteado, pero dentro de la región de separación, no en los extremos.

Aplicación a datos de la edad de la menarquia

El rango de datos es 14,4, y el de la región de separación es 4,2, lo cual es un 30% del total, mostrando que no hay mucha gravedad en la separación y se podría decir que la naturaleza de la probabilidad es creciente, pues a medida que aumenta la edad, hay mayor frecuencia de niñas que han tenido menarquia. Seguido a este análisis, se generó un par de seudo-observaciones ficticias a un par de edades a una distancia de 1.26 (30% de la Rs), así: (10.3,1) y (14.5,0), encontrando la estimación de parámetros (tabla 7).

Tabla 7. Parámetros estimados del modelo logístico para la edad de la menarquia

La edad es una variable significativa sobre la probabilidad de tener menarquia (Valor p = 1,6*10^-6). En la tabla 8 se ve la solución de Firth, usando la función logistf de R.

Tabla 8. Solución con método de Firth

En la tabla 9 se ve la solución bayesiana, usando la función MCMClogit de R:

Tabla 9. Solución con método Bayesiano

En los 3 casos el coeficiente que acompaña a la edad es positivo y significativo al 95% de confianza, lo cual indica un acierto en la estimación, así mismo, es significativo el término independiente. Sin embargo, puede decirse que el de Firth presenta más diferencias en relación al parámetro de la edad en comparación con los otros dos.

Discusión

La consecuencia más grave del problema de la separación en los modelos de regresión logística es el hecho de no permitir la estimación de máxima verosimilitud con el fin de realizar inferencias sobre la probabilidad de interés. Este trabajo aporta una solución adecuada al problema, probada vía simulación y aplicada a un caso donde se logra de forma clara y significativa una convergencia en los parámetros del modelo logístico.

Se observó que es mejor generar la sobreposición dentro de la región de separación y no en los extremos y con un bajo número de observaciones ficticias. Otra posible solución podría surgir al evaluar el movimiento de varias observaciones del mismo conjunto de datos hasta encontrar sobreposición, solución que debe validarse vía simulación. No siempre que la dispersión total de los datos sea grande, es grave la separación, en estos casos debe observarse la descompensación en el número de éxitos y de fracasos. Si existe mayor número de fracasos que éxitos, el modelo puede tener un crecimiento lento de la probabilidad, pero si es al contrario, puede crecer con mayor rapidez. Por ello, se recomienda en estos casos la solución propuesta, agregar un par de observaciones ficticias en un par de puntos dentro de la región de separación para conseguir la estimación del modelo buscado.

Referencias

1 Albert A, Anderson JA. On the existence of maximum likelihood estimates in logistic regression models. Biometrika 1984;71: 1-10.        [ Links ]

2 Christmann A, Rousseeuw PJ. Measuring overlap in binary regression. Computational Statistics and Data Analysis 2001; 37: 65-75.        [ Links ]

3 Christmann A, Rousseeuw PJ. Robustness against separation and outliers in logistic regression, Computational Statistics and Data Analysis 2003;43: 315-332.        [ Links ]

4 King E, Ryan TP. A preliminary investigation of maximum likelihood logistic regression versus Exact logisic Regression. American Statistical Association 2002; 56 (3): 163-170.        [ Links ]

5 Lesaffre E, Albert A. Partial Separation in Logistic Discrimination. Journal of the Royal Statistical Society. Series B (Methodological) 1989; 51(1): 109-116.        [ Links ]

6 Rindskopf D. Infinite parameter estimates in logistic regression: Opportunities, not problems. Journal of Educational and Behavioral Statistics 2002; 27(2): 147-161.        [ Links ]

7 Gentleman R, Ihaka R. R: A Language and Environment for Statistical Computing. R Development Core Team [internet] R Foundation for Statistical Computing: Vienna; 2009 [acceso 07 de noviembre de 2010]. Disponible en: www.R-project.org.        [ Links ]

8 Santner TJ, Duffy DE. A note on A. Albert and J. A. Anderson's conditions for the existence of maximum likelihood estimates in logistic regression models. Biometrika 1986; 73(3): 755-758.        [ Links ]

9 Ying So. A Tutorial on Logistic Regression [revista en internet]. Journal Of Marriage And The Family 1995; 57(4): 1-6. Disponible en: http://www.mendeley.com/research/a-tutorial-on-logisticregression/        [ Links ]

10 Heinze G, Shemper M. A solution to the problem of separation in logistic regression. Statist. Med 2002; 21:2409-2419.        [ Links ]

11 Firth D. Bias reduction, the Je_reys prior and glim. En: Fahrmeir L, Francis B, Gilchrist R, Tutz G, editores. Advances in glim and Statistical Modelling. New York: Springer-Verlag; 1992. p. 91- 100.        [ Links ]

Recibido: 16 de mayo de 2011.
Aprobado: 20 de agosto de 2011