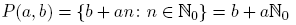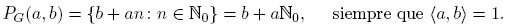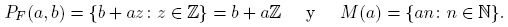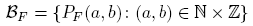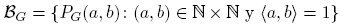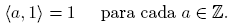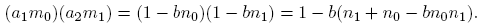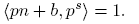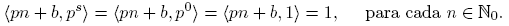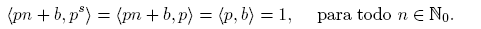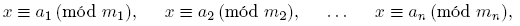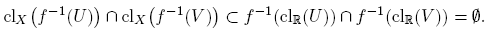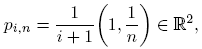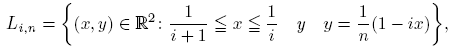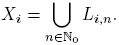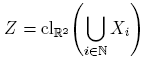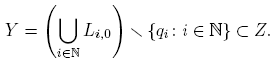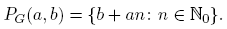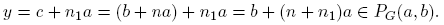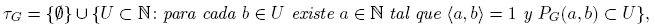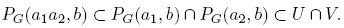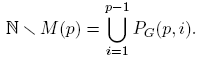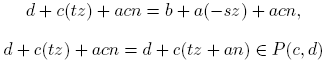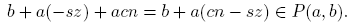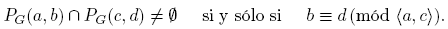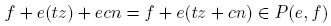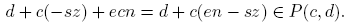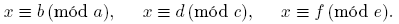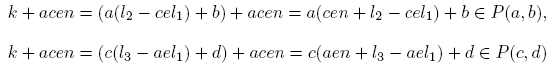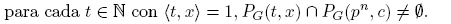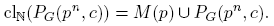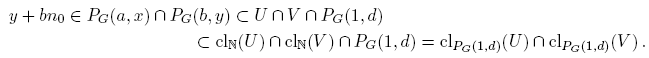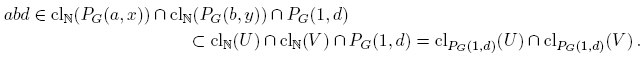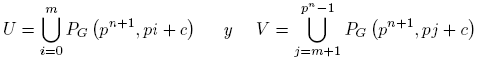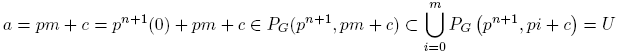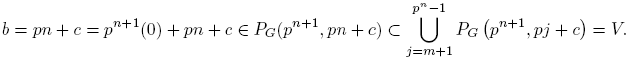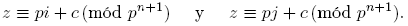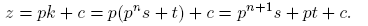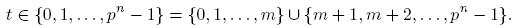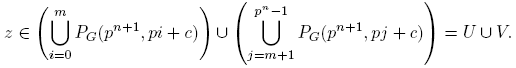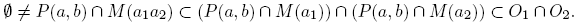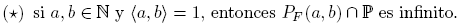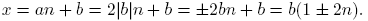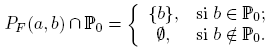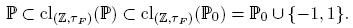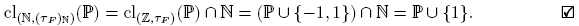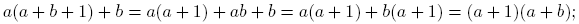1. Introducción
Denotamos por R, Z y N los conjuntos de los números reales, de los números enteros y de los números naturales, respectivamente. Además, N0 = N∪{0}. También denotamos por P el conjunto de los números primos, y suponemos que P ⊂ N. Dados a, b ∈ Z, en donde al menos uno de ellos es diferente de cero, el símbolo〈a, b〉denota el máximo común divisor de a y b. Para cada a, b ∈ N, consideramos las progresiones aritméticas
y
Para a ∈ N y b ∈ Z, también consideramos las progresiones aritméticas
Notemos que P(a, b) = PG (a, b) si y sólo si〈a, b〉= 1. Además, M(a) = P(a, a). En 1955 Furstenberg probó en [6] que la familia
es base de una topología τF en Z. También mostró que el espacio topológico (Z, τF ) es segundo numerable y T 4, por lo que es metrizable. Más aún, hizo ver que cada básico PF (a, b) es abierto y cerrado en (Z, τF ), así que este espacio es cero-dimensional y no conexo.
Tanto en 1959 como en 1962, Golomb probó en [7] y en [8] que la familia
es base de una topología τG en N (ver Teorema 3.2). En [12, Ejemplos 60 y 61, p. 82], cuya primera edición fue publicada en 1970, a τG se lo llama la “topología del entero primo relativo”. En el presente trabajo, al igual que en los artículos [13], [14], [15], [16], [17] y [18] de Szczuka, a τG lo llamamos la topología de Golomb, y decimos que el espacio topológico (N, τG ) es el espacio de Golomb.
En [7, Teoremas 2 y 3, p. 663] y [8, Teoremas 2 y 3, p. 180], Golomb probó que (N, τG ) es segundo numerable, T 2 y conexo (ver Teoremas 4.1, 4.11 y 4.17). Usando el hecho de que, para cada p ∈ P, el conjunto M(p) es cerrado en (N, τG ) (ver Teorema 4.2), Golomb probó en [7, Teorema 1, p. 663] y [8, Teorema 1, p. 180], que P es infinito (ver Teorema 4.3). Usando una fuerte herramienta de la Teoría Analítica de Números, Golomb probó en [7, Teoremas 6 y 7, p. 664] y [8, Teoremas 6 y 7, p. 181], que P es denso en (N, τG ) y tiene interior vacío (ver Teoremas 4.28 y 4.29).
La prueba de la conexidad de (N, τG ), como fue presentada por Golomb, utiliza argumentos propios de la Teoría de Números. Como se indica en [7, p. 663] y [8, p. 180] “una prueba de la conexidad de (N, τG ), que no utiliza argumentos de la Teoría de Números, fue presentada por Brown en abril de 1953, durante el congreso de la Sociedad Matemática Americana”, que se llevó a cabo en la ciudad de Nueva York. Brown estudió el espacio (N, τG ) antes que Golomb, pero no publicó sus resultados. El resumen de la plática de Brown, publicado en [2, p. 367] y en donde se bosqueja la manera de demostrar la conexidad de (N, τG ), motivó en 2017 a Clark, Lebowitz-Lockard y Pollack, a acuñar en [3] la siguiente noción.
Definición 1.1. Un espacio de Brown es un espacio topológico X tal que para cada dos subconjuntos abiertos y no vacíos U y V de X, tenemos que cl X (U) ∩ cl X (V) ≠ ∅. Si X es un espacio topológico y Y ⊂ X, decimos que Y es un espacio de Brown en X si Y, como subespacio de X, es de Brown.
Sea X un espacio topológico. Para simplificar, diremos que X es de Brown, en lugar de decir que X es un espacio de Brown. Si X es no numerable y su topología es la del complemento finito o bien la del complemento numerable, entonces X es de Brown. El siguiente resultado aparece en [3, Proposición 6].
Teorema 1.2. Todo espacio de Brown X es conexo.
Demostración. Si X no es conexo, entonces existen dos subconjuntos no vacíos U y V de X, abiertos y cerrados en X, tales que X = U ∪ V y U ∩ V = ∅. Entonces cl X (U) ∩ cl X (V ) = U ∩ V = ∅, lo cual contradice el hecho de que X es de Brown. ☑
En el presente trabajo damos una prueba explícita del hecho de que (N, τG ) es de Brown (ver Teorema 4.17). También probamos que, para cada d ∈ N, la progresión aritmética PG (1, d) es de Brown en (N, τG ) (ver Teorema 4.16).
En 1969 Kirch demostró en [9, Teorema 1, p. 169], que (N, τG ) no es localmente conexo. Formalmente, hizo ver que (N, τG ) no es localmente conexo en 1. Luego de esto definió, en el mismo artículo, una topología τK en N tal que τK ⊂ τG y (N, τK ) es conexo, T 2 y localmente conexo. Aunque Kirch fue el primero en probar que (N, τG ) no es localmente conexo, presentamos este hecho de manera más general, pues, como vemos en el Teorema 4.20, para ningún d ∈ N el conjunto PG (1, d) es conexo en pequeño o casi conexo en pequeño, en cada uno de sus puntos.
El presente trabajo está dividido en cuatro secciones. Luego de esta Introducción, en la Sección 2 presentamos una serie de nociones y resultados, propios de la Teoría de Números y de la Topología General, que serán necesarios para probar las propiedades topológicas del espacio (N, τG ), trabajo que se realiza en las Secciones 3 y 4. Conviene destacar que varios resultados presentados en la Sección 4 aparecen por vez primera. Incluimos en la Sección 4 una serie de preguntas abiertas.
2. Definiciones y resultados iniciales
En esta sección presentamos una serie de definiciones y resultados básicos que utilizaremos para probar los enunciados principales. La mayoría de los resultados, propios de la Teoría de Números y de la Topología General, son conocidos y se indica, en cada caso, una referencia adecuada. Un conjunto es numerable si tiene la misma cardinalidad que un subconjunto de N. Un conjunto es infinito numerable si tiene la misma cardinalidad que N.
2.1. Teoría de números
En la presente subsección damos por hecho que el lector tiene conocimientos básicos de la Teoría de Números, por lo que omitiremos varias demostraciones, remitiendo al lector interesado a textos clásicos como [1] y [11], o bien a uno más reciente como [5]. Si c, d ∈ Z y c divide a d, escribimos c | d. En caso contrario, escribimos c ∤ d. Si c, d ∈ N y c | d, entonces c ≦ d. Recordemos que el máximo común divisor de los enteros a y b, en donde al menos uno de ellos es diferente de cero, lo denotamos por〈a, b〉. Es claro que〈a, b〉∈ N, y que
Los dos resultados siguientes, aparecen probados en [11, Teorema 1.2, p. 5] y [11, Teorema 1.9, p. 9], respectivamente. El primero de ellos es conocido como el Algoritmo de la División.
Teorema 2.1. Si a, b ∈ Z con b ≠ 0, entonces existen dos enteros únicos q y r, tales que a = bq + r y 0 ≦ r < |b|.
Teorema 2.2. Si a, b, q, r ∈ Z son tales que a = bq + r, entonces〈a, b〉=〈b, r〉.
El resultado siguiente aparece probado en [11, Teoremas 1.3 y 1.4, p. 7-8].
Teorema 2.3. Si a, b ∈ Z y g =〈a, b〉, entonces existen n,m ∈ Z tales que g = an + bm. Más aún, si 1 es combinación lineal de a y b, entonces〈a, b〉= 1. Si d es una combinación lineal de a y b, entonces g | d.
Teorema 2.4. Supongamos que b, a 1, a 2 ∈ Z son tales que〈b, a 1〉=〈b, a 2〉= 1. Entonces 〈b, a 1 a 2〉= 1. En particular, para cada n ∈ N,〈b, a 1 n 〉=〈b, a 2 n 〉= 1.
Demostración. Como 1 =〈b, a 1〉=〈b, a 2〉, por el Teorema 2.3 existen n 0, n 1,m 0,m 1 ∈ Z tales que 1 = bn 0 + a 1 m 0 y 1 = bn 1 + a 2 m 1. Entonces,
Haciendo n = n 1 +n 0 − bn 0 n 1 y m = m 0 m 1, tenemos que 1 = bn +(a 1 a 2)m. Luego 1 es una combinación lineal de b y a 1 a 2 y, por la segunda parte del Teorema 2.3,〈b, a 1 a 2〉. En particular, cuando a 1 = a 2, 〈b, a 1 2〉=〈b, a 2 2〉= 1 y, por inducción, para cada n ∈ N tenemos que 〈b, a 1 n 〉=〈b, a 2 n 〉= 1. ☑
Diremos que p ∈ N \ {1} es un número primo si sus únicos divisores positivos son 1 y p. Recordemos que P denota al conjunto de los números primos.
Teorema 2.5. Sean p ∈ P y a ∈ Z. Si p ∤ a, entonces〈p, a〉= 1. En particular, para cada a ∈ {1, 2, . . . , p − 1}, tenemos que〈p, a〉= 1.
Demostración. Sea d =〈p, a〉. Entonces d ∈ N y d | p, de manera que d = 1 o bien d = p, ya que p es un número primo. Si d = p, sucede que p | a, contradiciendo que p ∤ a. Luego d = 1 y〈p, a〉= 1. Ahora tomemos a ∈ {1, 2, . . . , p − 1}. Entonces a < p. Si p | a, resulta que p ≦ a, lo cual es una contradicción. Por tanto, p ∤ a y, así,〈p, a〉= 1. ☑
Una prueba del siguiente resultado aparece en [11, Teorema 1.15, p. 23].
Teorema 2.6. Sea p ∈ P. Si u, v ∈ Z son tales que p | uv, entonces p | u o bien p | v.
El siguiente resultado aparece, sin demostración, tanto en [9, p. 169] como en [13, p. 902]. Lo utilizaremos más adelante, y presentemos aquí una prueba del mismo.
Teorema 2.7. Sean p ∈ P y b ∈ Z tales que〈p, b〉= 1. Entonces, para toda n, s ∈ N0,
En particular si b ∈ N, entonces para cada m ∈ PG (p, b) y todo s ∈ N0, tenemos que〈m, ps 〉= 1.
Demostración. Si s = 0, por (1)
Si s = 1, entonces, como〈p, b〉= 1, por el Teorema 2.2
Supongamos ahora que existen s 0 ∈ N \ {1} y n0 ∈ N0 tales que g =〈pn 0 + b, ps 0〉> 1. Sea q ∈ P tal que q | g. Luego q | (pn 0 + b) y q | ps 0 . Como p, q ∈ P y q | ps 0 , por el Teorema 2.6, q = p. Así, q | (pn 0 + b) y q | p, de donde q |〈pn 0 + b, p〉y, por (3), q | 1, lo cual es una contradicción. Por lo tanto〈pn + b, ps 〉= 1, para todo s, n ∈ N0. Esto termina la primera parte del teorema. La segunda parte es una consecuencia inmediata de la primera. ☑
2.2. Congruencias
Ahora veamos algunos resultados sobre las congruencias numéricas. Supongamos que a, b ∈ N y m ∈ N \ {1}. Si a es congruente con b módulo m, escribimos a ≡ b (mód m). De lo contrario, escribimos a ≢ b (mód m). Sean a, b ∈ N, con a ≠ 1. Si c ∈ P(a, b), entonces c ≡ b (mód a). Si c ≡ b (mód a) y c ≧ b, entonces c ∈ P(a, b). Tenemos también el siguiente resultado.
Teorema 2.8. Sean a, b ∈ N. Entonces P(a, b) ⊂ PF (a, b). Más aún, si b ≦ a entonces PF (a, b) ∩ N = P(a, b).
Demostración. Sea c ∈ PG (a, b). Entonces c = am + b, para algún m ∈ N0. Como N ⊂ N0 ⊂ Z, se sigue que b y m son enteros tales que c = am + b. Luego c ∈ PF (a, b). Por tanto, P(a, b) ⊂ PF (a, b). Como P(a, b) ⊂ N, tenemos que P(a, b) ⊂ PF (a, b) ∩ N.
Supongamos ahora que b ≦ a. Sean y ∈ PF (a, b) ∩ N y z ∈ Z tales que y = az + b. Si z ≦ −1, entonces az ≦ bz ≦ −b, de donde y = az+b ≦ 0, lo cual contradice el que y ∈ N. Luego z ≧ 0 y, así, y ∈ P(a, b). Esto prueba que PF (a, b) ∩ N ⊂ P(a, b) y, como la otra contención también es cierta, PF (a, b) ∩ N = P(a, b). ☑
Sean a, b ∈ N. Si a < b, entonces algunos elementos de PF (a, b) ∩ N son menores que b y, por tanto, no se encuentran en P(a, b). Por ejemplo, b − a = a(−1) + b ∈ (PF (a, b) ∩ N) \ P(a, b).
En [1, Teorema 5.10(c), p. 110] se prueba que, para cada m ∈ N \ {1}, el conjunto Z se divide en justo m clases de equivalencia distintas, a saber [0], [1], . . . , [m−1]. Esto motiva la siguiente definición.
Definición 2.9. Sea m ∈ N \ {1}. Un conjunto A de m números enteros es un sistema completo de residuos módulo m, si cada elemento de A es un representante de una y solo una de las clases [0], [1], . . . , [m− 1].
Sea m ∈ N \ {1}. Es claro que el conjunto {0, 1, 2, . . . ,m−1} es un sistema completo de residuos módulo m. A continuación, presentamos otras propiedades de las congruencias, que se utilizarán más adelante. Una demostración del siguiente resultado aparece en [5, Lema 2.4.3, p. 24].
Teorema 2.10. Sean m ∈ N \ {1} y a, b, c, d ∈ Z. Entonces:
1) Si a ≡ b (mód m) y c ≡ d (mód m), entonces a+c ≡ b+d (mód m). En particular, a ≡ b (mód m) si y sólo si a + x ≡ b + x (mód m), para cualquier entero x.
2) Si a ≡ b (mód m) y d | m, con d > 1, entonces a ≡ b (mód d).
3) Si c ∈ N, entonces a ≡ b (mód m) si y sólo si ac ≡ bc (mód mc).
Decimos que los enteros m 1,m 2, . . . ,mn ∈ N \ {1} son primos relativos dos a dos si para cada i, j ∈ {1, 2, . . . , n} con i ≠ j,〈mi,mj 〉= 1. El siguiente resultado es el Teorema Chino del Residuo. Una prueba del mismo aparece en [11, Teorema 2.18, p. 64].
Teorema 2.11. Supongamos que m1,m2, . . . ,mn ∈ N \ {1}. Entonces todo sistema de congruencias lineales del tipo
en los cuales los módulos m1,m2, . . . ,mn son primos relativos dos a dos, tiene una única solución con módulo igual al producto de los módulos. Es decir, existe un único entero a tal que x ≡ a (mód m1m2 ・ ・ ・mn ).
2.3. Topología general
En la presente subsección damos por hecho que el lector tiene conocimientos básicos de la Topología General, por lo que omitiremos varias demostraciones, remitiendo al lector interesado a textos clásicos como [4] y [19]. Si X es un espacio topológico y A ⊂ X, denotamos por int X (A) y cl X (A) el interior y la cerradura de A en X, respectivamente. En particular, si A ⊂ N, el símbolo clN(A) denota la cerradura de A en (N, τG ). Si X es un espacio topológico y A ⊂ Y ⊂ X, entonces cl Y (A) = cl X (A) ∩ Y.
A continuación enlistamos una serie de axiomas de separación que se utilizan en el presente trabajo.
Definición 2.12. Un espacio topológico X es:
1) T 1, si para cada x ∈ X el conjunto {x} es cerrado en X;
2) T 2 o Hausdorff, si para cada x, y ∈ X con x ≠ y, existen abiertos U y V en X tales que x ∈ U, y ∈ V y U ∩ V = ∅;
3) T 2½ o completamente Hausdorff, si para cada x, y ∈ X con x ≠ y, existen abiertos U y V en X tales que x ∈ U, y ∈ V y cl X (U) ∩ cl X (V) = ∅;
4) regular, si para toda x ∈ X y cada cerrado C en X con x ∉ C, existen abiertos U y V en X tales que x ∈ U, C ⊂ V y U ∩ V = ∅;
5) T 3, si X es regular y T 1;
6) T 4, si X es T 1 y para cada dos cerrados C y D en X con C ∩ D = ∅, existen dos abiertos U y V en X tales que C ⊂ U, D ⊂ V y U ∩ V = ∅.
Se sabe que T 4 ⇒ T 3 ⇒ T 2½ ⇒ T 2 ⇒ T 1, y que ninguna de las implicaciones anteriores es reversible (ver [10, Ejemplos VII.4.2, VII.5.2, VII.6.8, VII.7.5 y VII.8.10]). De las correspondientes definiciones de espacio de Brown y de espacio T 2½, se tiene el siguiente resultado.
Teorema 2.13. Ningún espacio de Brown, con al menos dos puntos, es T 2½.
Por el resultado anterior, ningún espacio de Brown es metrizable. Sean X un espacio topológico y x ∈ X. Decimos que X es indiscreto en x, o que x es un punto indiscreto de X, si X es el único subconjunto abierto en X que contiene a x. Notemos que X posee la topología indiscreta si y sólo si cada punto de X es indiscreto. El siguiente resultado se prueba en [3, Proposición 6].
Teorema 2.14. En un espacio topológico X se cumplen las siguientes propiedades:
1) si X contiene un punto indiscreto, entonces X es de Brown;
2) si X es de Brown, entonces X es regular si y sólo si X posee la topología indiscreta.
Notemos que los espacios T 1, con al menos dos puntos, no poseen puntos indiscretos. Utilizando esto y el Teorema 2.14, resulta que ningún espacio conexo y T 3, con al menos dos puntos, es de Brown. De manera más general, ningún espacio conexo, regular y sin puntos indiscretos, es de Brown. Esto implica que el recíproco del Teorema 1.2 no es cierto.
Sean X y Y dos espacios topológicos y f: X → Y una función continua y suprayectiva. No es difícil probar que si X es de Brown, entonces Y también es de Brown. Esto implica que si {Xs : s ∈ S} es una familia de espacios topológicos y el producto cartesiano Π s∈S Xs , con la topología producto, es de Brown, entonces cada Xs es de Brown. Tampoco es difícil probar que si, en su lugar, suponemos que cada Xs es de Brown, entonces Π s∈S Xs también es de Brown.
En el Teorema 4.17 mostramos que (N, τG ) es de Brown, y en el Teorema 4.11, que dicho espacio es T 2. Combinando esto con el Teorema 2.13, tenemos que (N, τG ) es un espacio T 2 que no es T 2½. Ahora bien, en el Teorema 4.18 exhibimos subespacios del espacio de Brown (N, τG ), que no son de Brown. Por tanto, ser de Brown no es una propiedad hereditaria.
Considerando a R con la topología usual τU , resulta que si X es de Brown, entonces toda función continua f: X → R es constante. En efecto, si f no es constante, existen x, y ∈ X con x ≠ y tales que f(x) ≠ f(y). Como (R, τU ) es T 2½, existen abiertos U y V en R tales que f(x) ∈ U, f(y) ∈ V y clR(U) ∩ clR(V ) = ∅. Por la continuidad de f, f −1(U) y f −1(V ) son abiertos en X tales que x ∈ f −1(U), y ∈ f −1(V ) y
Como esto contradice el que X es de Brown, f es constante.
Utilizando [4, Teorema 3.8.2 y Corolario 6.1.4], se tiene el siguiente resultado, que habla sobre la cardinalidad de un conjunto conexo y T 3.
Teorema 2.15. Si X es conexo, no vacío, numerable y T3, entonces X posee solamente un elemento.
Sean X un espacio topológico y x ∈ X. La componente (conexa) de X que tiene a x, es la unión de todos los subconjuntos conexos de X que tienen a x. La casicomponente de X que tiene a x, es la intersección de todos los subconjuntos abiertos y cerrados de X que tienen a x. Haremos uso de estos términos, y de los que aparecen en la siguiente definición.
Definición 2.16. Un espacio topológico X
1) es hereditariamente disconexo, si ningún subconjunto conexo y no vacío de X, tiene más de un elemento;
2) está totalmente separado, si para cada x, y ∈ X con x ≠ y, existen abiertos U y V en X tales que x ∈ U, y ∈ V, X = U ∪ V y U ∩ V = ∅;
3) es cero-dimensional, si X es T 1 y posee una base cuyos elementos son abiertos y cerrados en X.
A los espacios hereditariamente disconexos se los suele también llamar totalmente disconexos. En [4, Teorema 6.2.1] se prueba que todo espacio cero-dimencional es hereditariamente disconexo. En [4, Teorema 6.2.9] se prueba que si X es hereditariamente disconexo y localmente compacto, entonces X es cero-dimensional. Notemos que un espacio X es hereditariamente disconexo si y sólo si, para cada x ∈ X la componente Cx de X que tiene a x es justo el conjunto {x}. Notemos también que X está totalmente separado si y sólo si, para cada x ∈ X la casicomponente Qx de X que tiene a x coincide con el conjunto {x}. Por [4, Teorema 6.1.22], Cx ⊂ Qx para cada x ∈ X, así que los espacios totalmente separados son hereditariamente disconexos. Si X es compacto y T 2, por [4, Teorema 6.1.23], Cx = Qx para cada x ∈ X. Por tanto, en los espacios compactos y T 2, las nociones de espacio hereditariamente disconexo y de espacio totalmente separado coinciden.
Sean X un espacio topológico y a, b ∈ X. Decimos que X es conexo entre a y b si para cada par de abiertos U y V en X tales que a ∈ U, b ∈ V y U ∩ V = ∅, se sigue que X ≠ U ∪ V. No es difícil probar que si X es T 2, entonces X está totalmente separado si sólo si para cada a, b ∈ X con a ≠ b, X no es conexo entre a y b.
A continuación enlistamos una serie de axiomas de conexidad que se utilizarán más adelante. Todos ellos garantizan la existencia de conjuntos conexos con interior no vacío.
Definición 2.17. Sean X un espacio topológico y x ∈ X. Diremos que X es:
1) conexo en pequeño en x, si para todo abierto U en X con x ∈ U, existe un subconjunto conexo V de X tal que x ∈ int X (V ) ⊂ V ⊂ U;
2) localmente conexo en x, si para cada abierto U en X con x ∈ U, existe un abierto y conexo V en X tal que x ∈ V ⊂ U;
3) casi conexo en pequeño en x, si para cada abierto V en X con x ∈ V, existe un subconjunto conexo y cerrado U en X tal que int X (U) ≠ ∅ y U ⊂ V ;
4) casi conexo en pequeño, si X es casi conexo en pequeño en cada uno de sus puntos;
5) localmente conexo, si X es localmente conexo en cada uno de sus puntos.
Es claro que si X es localmente conexo en x, entonces X es conexo en pequeño en x. Ahora mostraremos que el recíproco de esta implicación no es cierto. Vamos a describir un subespacio Z de R2, con la topología usual. Para cada i ∈ N, sean 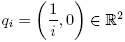 y Li
,0 el segmento de recta con extremos qi
y qi
+1. Para toda (i, n) ∈ N × N, consideremos el punto
y Li
,0 el segmento de recta con extremos qi
y qi
+1. Para toda (i, n) ∈ N × N, consideremos el punto
así como el segmento de recta Li,n con extremos pi,n y qi . Es decir, para cada (i, n) ∈ N × N,
donde 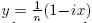 es la ecuación de la recta que pasa por los puntos pi,n
y qi
. Definamos, para cada i ∈ N, el conjunto
es la ecuación de la recta que pasa por los puntos pi,n
y qi
. Definamos, para cada i ∈ N, el conjunto
Entonces
es un espacio topológico compacto y conexo que, además, es conexo en pequeño en el punto (0, 0) y no es localmente conexo en (0, 0). El espacio Z, llamado la escoba infinita nula, aparece en [19, Ejemplo 27.15, p. 201], aunque no se indican los detalles de porque dicho espacio es conexo en pequeño en (0, 0) y no localmente conexo en (0, 0). Por consiguiente, la conexidad en pequeño en un punto, no implica la conexidad local en dicho punto. En [19, Teorema 27.16, p. 201] se prueba que si X es conexo en pequeño en cada uno de sus puntos, entonces X es localmente conexo. Con respecto al espacio Z que hemos descrito, sea
Notemos que Z es casi conexo en pequeño en cada punto p ∈ Y, y no es conexo en pequeño en p. Notemos también que si X es un espacio T 3 y conexo en pequeño en un punto x ∈ X, entonces X es casi conexo en pequeño en x.
3. La topología de Golomb
Recordemos que para cada a, b ∈ N con〈a, b〉= 1,
En el siguiente teorema, enlistamos tres propiedades de los conjuntos anteriormente definidos.
Teorema 3.1. Para cada (a, b) ∈ N × N con〈a, b〉= 1, se satisfacen las siguientes propiedades:
1) PG (a, b) es infinito, b ∈ PG (a, b) y PG (1, 1) = N;
2) si c ∈ PG (a, b), entonces〈a, c〉= 1 y PG (a, c) ⊂ PG (a, b);
3) si a 1, a 2 ∈ N y〈b, a 1〉=〈b, a 2〉= 1, entonces〈b, a 1 a 2〉= 1 y PG (a 1 a 2, b) ⊂ PG (a 1, b) ∩ PG (a 2, b).
Demostración. Para ver 1) y 2), sea (a, b) ∈ N×N con〈a, b〉= 1. Entonces b = a(0)+b ∈ PG (a, b), es decir, b ∈ PG (a, b). Para probar la infinitud de PG (a, b), sea f: N0 → PG (a, b) la función definida como f(m) = am+ b, para cada m ∈ N0. Si n,m ∈ N0 son tales que f(n) = f(m), entonces an + b = am + b, por lo que an = am y, como a ∈ N, la igualdad am = an implica que n = m. Esto prueba que f es inyectiva. Claramente f es sobreyectiva, así que f es biyectiva. Luego N0 y PG (a, b) tienen la misma cardinalidad, de donde PG (a, b) es infinito numerable. Para ver que PG (1, 1) = N, sea n ∈ N. Como n = 1(n − 1) + 1 y (n − 1) ∈ N0, se sigue que n ∈ PG (1, 1). Luego N ⊂ PG (1, 1). Como también PG (1, 1) ⊂ N, concluimos que PG (1, 1) = N. Esto prueba 1).
Para probar 2), sea c ∈ PG (a, b). Entonces existe n ∈ N0 tal que c = b + na. Por el Teorema 2.2,〈c, a〉=〈a, b〉= 1. Si y ∈ PG (a, c), entonces existe n 1 ∈ N0 tal que y = c+n 1 a. Luego
Esto prueba que PG (a, c) ⊂ PG (a, b) y 2) se cumple.
Para probar 3), sean b ∈ N y a 1, a 2 ∈ N tales que〈b, a 1〉=〈b, a 2〉= 1. Por el Teorema 2.4,〈b, a 1 a 2〉= 1. Si x ∈ PG (a 1 a 2, b), entonces existe n ∈ N0 tal que x = b + n(a 1 a 2). Por tanto, x = b + (na 2)a 1 ∈ PG (a 1, b) y x = b + (na 1)a 2 ∈ PG (a 2, b). Luego x ∈ PG (a 1, b) ∩ PG (a 2, b). Esto termina la prueba de 3). ☑
Consideremos ahora la familia
Como indicamos en la Introducción, Golomb probó en [7] y en [8] que BG es base de la topología τG en N que se indica en el siguiente resultado.
Teorema 3.2. La familia
es una topología en N. Además BG ⊂ τG y BG es una base del espacio topológico (N, τG ).
Demostración. Vamos a probar primero que τG es una topología. Por definición ∅ ∈ τG . Para cada b ∈ N, 1 ∈ N es tal que〈1, b〉= 1 y PG (1, b) ⊂ N. Por tanto, N ∈ τG . Sea {Ui : i ∈ I} una familia de elementos en τG . Dada b ∈ ∪ i∈I Ui , existe i 0 ∈ I tal que b ∈ Ui 0 . Como Ui 0 ∈ τG , existe a ∈ N tal que〈a, b〉= 1 y PG (a, b) ⊂ Ui 0 . En vista de que Ui 0 ⊂∪ i∈I Ui , deducimos que PG (a, b) ⊂∪ i∈I Ui . Esto prueba que ∪ i∈I Ui ∈ τG .
Ahora supongamos que U, V ∈ τG . Si U ∩ V = ∅, entonces U ∩ V ∈ τG . Consideremos, por tanto, que U ∩ V ≠ ∅, y sea b ∈ U ∩ V. Como b ∈ U, existe a 1 ∈ N tal que〈b, a 1〉= 1 y PG (a 1, b) ⊂ U. Como también b ∈ V, existe a 2 ∈ N tal que〈b, a 2〉= 1 y PG (a 2, b) ⊂ V. Notemos que a 1 a 2 ∈ N. Además, por la propiedad 3) del Teorema 3.1,〈b, a 1 a 2〉= 1 y
Esto prueba que U ∩ V ∈ τG , por lo que τG es una topología en N.
Para mostrar que BG ⊂ τG , sea PG (a, b) ∈ BG . Entonces a, b ∈ N y〈a, b〉= 1. Si c ∈ PG (a, b), por la propiedad 2) del Teorema 3.1,〈a, c〉= 1 y PG (a, c) ⊂ PG (a, b). Luego PG (a, b) ∈ τG . Esto prueba que BG ⊂ τG .
Tomemos ahora U ∈ τG y b ∈ U. Entonces existe a ∈ N tal que〈a, b〉= 1 y PG (a, b) ⊂ U. Como PG (a, b) ∈ BG y b ∈ PG (a, b) ⊂ U, resulta que U es una unión de elementos de BG . Como cada elemento de BG es abierto en (N, τG ), tenemos que BG es una base del espacio topológico (N, τG ). ☑
4. Propiedades del espacio (N, τG )
Vamos ahora a mostrar una serie de propiedades del espacio de Golomb (N, τG ). Los Teoremas 4.1, 4.2, 4.3, 4.11, 4.28 y 4.29 se mencionaron en la Introducción, y fueron probados por Golomb.
Teorema 4.1. (N, τG ) es segundo numerable. Más aún, cada subconjunto abierto y no vacío en (N, τG ) es infinito.
Demostración. Por el Teorema 3.2, BG es una base del espacio topológico (N, τG ). Sea A = {(a, b) ∈ N × N:〈a, b〉= 1}. Como N es numerable, N × N también es numerable. Entonces A ⊂ N × N es numerable. Ahora consideremos la función g: A → BG definida, para (a, b) ∈ A, como g(a, b) = PG (a, b). Es claro que g es una función sobreyectiva y, como A es numerable, BG es numerable. Por tanto (N, τG ) es segundo numerable.
Sean U un subconjunto abierto y no vacío en (N, τG ) y b ∈ U. Como BG es una base de (N, τG ), existe a ∈ N tal que〈a, b〉= 1 y PG (a, b) ⊂ U. Por la propiedad 1) del Teorema 3.1, PG (a, b) es infinito. Luego U es infinito. ☑
Teorema 4.2. Para cada p ∈ P, M(p) es cerrado en (N, τG).
Demostración. Como p ∈ P, por el Teorema 2.5,〈p, i〉= 1 para todo i ∈ {1, 2, . . . , p−1}. Por tanto cada conjunto PG (p, i) es abierto en (N, τG ). Además,
La unión ∪ p−1 i=1 PG (p, i) es un abierto en (N, τG ). Entonces N \ M(p) es abierto en (N, τG ) y, así, M(p) es cerrado en (N, τG ). ☑
Teorema 4.3. El conjunto P es infinito.
Demostración. Por el Teorema de Factorización Única, todo número natural distinto de 1 es múltiplo de algún número primo. Por tanto
Si P es finito, por el Teorema 4.2, ∪ p∈P M(p) es una unión finita de subconjuntos cerrados en (N, τG ). Luego ∪ p∈P M(p) es cerrado en (N, τG ) y, por tanto, N \ {1} es cerrado en (N, τG ). Entonces {1} es abierto en (N, τG ). Pero esto contradice el hecho de que los subconjuntos abiertos y no vacíos de (N, τG ) son infinitos. Por lo tanto, P es infinito. ☑
El siguiente resultado da una condición necesaria y suficiente para que dos elementos de la base BF se intersequen.
Teorema 4.4. Sean a, c ∈ N y b, d ∈ Z. Entonces PF (a, b) ∩ PF (c, d) ≠ ∅ si y sólo si〈a, c〉| (b − d).
Demostración. Supongamos que PF (a, b)∩PF (c, d) ≠ ∅. Sean x, y ∈ Z tales que ax+b = cy + d. Luego b − d = cy + a(−x), por lo que b − d es una combinación lineal de a y c. Entonces, por la tercera parte del Teorema 2.3,〈a, c〉| (b − d).
Supongamos ahora que〈a, c〉| (b − d). Entonces existe z ∈ Z tal que b − d = z〈a, c〉. Por la primera parte del Teorema 2.3, existen s, t ∈ Z tales que〈a, c〉= as + ct. Luego b − d = asz + ctz, de donde d + c(tz) = b + a(−sz). Notemos que d + c(tz) ∈ PF (c, d) y b + a(−sz) ∈ PF (a, b). Luego PF (a, b) ∩ PF (c, d) ≠ ∅. ☑
En la demostración del siguiente resultado utilizamos la Propiedad Arquimediana, la cual dice que si a, b ∈ R y a > 0, entonces existe n ∈ N tal que an > b.
Teorema 4.5. Sean a, b, c, d ∈ N. Entonces P(a, b)∩P(c, d) ≠ ∅ si y sólo si〈a, c〉| (b−d).
Demostración. Supongamos que P(a, b) ∩ P(c, d) ≠ ∅. Sean x, y ∈ N tales que ax + b = cy + d. Luego b − d = cy + a(−x), por lo que b − d es una combinación lineal de a y c. Entonces, por la tercera parte del Teorema 2.3,〈a, c〉| (b − d).
Supongamos ahora que〈a, c〉| (b − d). Entonces existe z ∈ Z tal que b − d = z〈a, c〉. Por la primera parte del Teorema 2.3, existen s, t ∈ Z tales que〈a, c〉= as + ct. Luego b − d = asz + ctz, de donde d + c(tz) = b + a(−sz). Por la Propiedad Arquimediana, existen n 1, n 2 ∈ N tales que an 1 > −tz y cn 2 > sz. Sea n = máx{n 1, n 2}. Entonces an + tz y cn − sz son números naturales. Además
y
Luego, P(c, d) ∩ P(a, b) ≠ ∅. ☑
Corolario 4.6. Sean a, b, c ∈ N. Si〈a, c〉= 1, entonces P(a, b) ∩M(c) ≠ ∅.
Demostración. Como M(c) = P(c, c) y〈a, c〉= 1, tenemos que〈a, c〉| (b − c). Entonces, por el Teorema 4.5, P(a, b) ∩M(c) = P(a, b) ∩ P(c, c) ≠ ∅. ☑
Teorema 4.7. Sean a, b, c, d ∈ N tales que〈a, b〉=〈c, d〉= 1. Entonces PG (a, b) ∩ PG (c, d) ≠ ∅ si y sólo si〈a, c〉| (b − d).
Demostración. Supongamos que PG (a, b) ∩ PG (c, d) ≠ ∅. Entonces P(a, b) ∩ P(c, d) ≠ ∅ y, por el Teorema 4.5,〈a, c〉| (b − d). Supongamos ahora que〈a, c〉| (b − d). Entonces, por el Teorema 4.5, P(a, b)∩P(c, d) ≠ ∅.Como〈a, b〉=〈c, d〉= 1, tenemos que P(a, b) = PG (a, b) y P(c, d) = PG (c, d). Luego PG (a, b) ∩ PG (c, d) ≠ ∅. ☑
El Teorema 4.7 aparece en la parte 2. de [12, Ejemplos 60 y 61, p. 82], y da una condición necesaria y suficiente para que dos elementos de la base BG se intersequen. Sean a, b, c, d ∈ N tales que〈a, b〉=〈c, d〉= 1. Si〈a, c〉≠ 1 entonces, por el Teorema 4.7,
Teorema 4.8. Sean a, b, c, d, e, f ∈ N. Si〈a, c〉=〈a, e〉=〈c, e〉= 1, entonces P(a, b) ∩ P(c, d) ∩ P(e, f) ≠ ∅.
Demostración. Supongamos que a = 1. Entonces P(a, b) = {b+n: n ∈ N0} es el conjunto de números naturales mayores o iguales a b. Sean 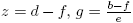 y s, t ∈ Z tales que 1 =〈c, e〉= cs+et. Luego d−f = (cs+et)z = csz+etz, de donde f +e(tz) = d+c(−sz). Por la Propiedad Arquimediana, existen n
1, n
2, n
3 ∈ N tales que cn
1 > −tz, en
2 > sz y cn
3 > −tz+g. Sea n = máx{n
1, n
2, n
3}. Entonces cn ≧ cn
1 > −tz, por lo que cn+tz ∈ N. También en ≧ en
2 > sz, de donde en − sz ∈ N. Además cn ≧ cn
3 > −tz + g, por lo que
y s, t ∈ Z tales que 1 =〈c, e〉= cs+et. Luego d−f = (cs+et)z = csz+etz, de donde f +e(tz) = d+c(−sz). Por la Propiedad Arquimediana, existen n
1, n
2, n
3 ∈ N tales que cn
1 > −tz, en
2 > sz y cn
3 > −tz+g. Sea n = máx{n
1, n
2, n
3}. Entonces cn ≧ cn
1 > −tz, por lo que cn+tz ∈ N. También en ≧ en
2 > sz, de donde en − sz ∈ N. Además cn ≧ cn
3 > −tz + g, por lo que 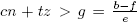 , luego e(tz + cn) > b − f, de donde f + e(tz + cn) > b. Así, f + e(tz + cn) ∈ P(a, b). Como f + e(tz) + ecn = d + c(−sz) + ecn, tenemos que
, luego e(tz + cn) > b − f, de donde f + e(tz + cn) > b. Así, f + e(tz + cn) ∈ P(a, b). Como f + e(tz) + ecn = d + c(−sz) + ecn, tenemos que
y
Luego f + e(tz) + ecn ∈ P(a, b) ∩ P(c, d) ∩ P(e, f), probando así que P(a, b) ∩ P(c, d) ∩ P(e, f) ≠ ∅. Si c = 1 o bien e = 1, procediendo de manera similar se prueba que P(a, b) ∩ P(c, d) ∩ P(e, f) ≠ ∅. Supongamos, por tanto, que a ≧ 2, c ≧ 2 y e ≧ 2. Consideremos el sistema de congruencias lineales
Como〈a, c〉=〈a, e〉=〈c, e〉= 1, por el Teorema Chino del Residuo (Teorema 2.11), existe un único entero k tal que x ≡ k (mód ace). Sean l 1, l 2, l 3, l 4 ∈ Z tales que x = acel 1+k, x = al 2+b, x = cl 3+d y x = el 4+f. Luego acel 1+k = al 2+b, acel 1+k = cl 3+d y acel 1+k = el 4+f, de donde k = a(l 2−cel 1)+b, k = c(l 3−ael 1)+d y k = e(l 4−acl 1)+f. Por tanto, k ≡ b (mód a), k ≡ d (mód c) y k ≡ f (mód e).
Por la Propiedad Arquimediana, existen n 1, n 2, n 3 ∈ N tales que cen 1 > cel 1−l 2, aen 2 > ael 1 −l 3 y acn 3 > acl 1 −l 4. Entonces n = máx{n 1, n 2, n 3} es un número natural tal que cen + l 2 − cel 1, aen + l 3 − ael 1 y acn + l 4 − acl 1 son números naturales. Luego
y
Así, k + acen ∈ P(a, b) ∩ P(c, d) ∩ P(e, f), de donde P(a, b) ∩ P(c, d) ∩ P(e, f) ≠ ∅. ☑
Como una aplicación del Teorema 4.5 tenemos el siguiente resultado, el cual aparece en [13, Lema 4.1, p. 904].
Teorema 4.9. Sean a, b, c, d ∈ N con b < a. Si P(a, b) ∩ P(c, d) ≠ ∅ y a | c, entonces P(c, d) ⊂ P(a, b).
Demostración. Como P(a, b) ∩ P(c, d) ≠ ∅, por el Teorema 4.5〈a, c〉| (b−d). Sea n ∈ N tal que c = an. Entonces ha, ci = ha, ani = ah1, ni = a. Luego a | (b − d) y, como a > b ≧ 1, tenemos que b ≡ d (mód a). Notemos que a ≧ 2 y c = an implican que c ≧ 2. Sea y ∈ P(c, d). Entonces y ∈ N, c | (y − d) y, como a | c, resulta que a | (y − d). Luego y ≡ d (mód a). Ahora bien, como b ≡ d (mód a) y y ≡ d (mód a), se tiene que y ≡ b (mód a). Luego y ∈ PF (a, b) ∩ N y, por el Teorema 2.8, y ∈ P(a, b). ☑
Como una aplicación del Teorema 4.7, tenemos el siguiente resultado.
Teorema 4.10. Sean a, x, y ∈ N tales que x ≠ y, máx{x, y} < a, 〈a, x〉=〈a, y〉= 1. Entonces PG (a, x) y PG (a, y) son abiertos en (N, τG ) tales que x ∈ PG (a, x), y ∈ PG (a, y) y PG (a, x) ∩ PG (a, y) = ∅. Además y ∉ clN(PG (a, x)) .
Demostración. Sean c = máx{x, y} y d = mín{x, y}. Notemos que〈a, a〉= a y que 1 ≦ d < c < a. Como〈a, x〉=〈a, y〉= 1, PG (a, x) y PG (a, y) son abiertos en (N, τG ) tales que x ∈ PG (a, x) y y ∈ PG (a, y). Supongamos que PG (a, x)∩PG (a, y) ≠ ∅. Entonces, por el Teorema 4.7, a | (x−y). Esto implica que a | (c−d). Ahora bien, al ser a y c−d enteros positivos, de a | (c − d) se sigue que a ≦ c − d < c. Luego a < c, lo cual contradice la desigualdad c < a. Esto prueba que PG (a, x)∩PG (a, y) = ∅ y que y ∉ clN(PG (a, x)) . ☑
El siguiente resultado es consecuencia del Teorema 4.10.
Teorema 4.11. (N, τG ) es T 2.
Demostración. Sean x, y ∈ N con x ≠ y, Como P es infinito, existe p ∈ P tal que máx{x, y} < p. Por el Teorema 2.5,〈p, x〉=〈p, y〉= 1. Luego, por el Teorema 4.10, PG (p, x) y PG (p, y) son abiertos en (N, τG ) tales que x ∈ PG (p, x), y ∈ PG (p, y) y PG (p, x) ∩ PG (p, y) = ∅. Por tanto, (N, τG ) es T 2. ☑
Sean a, x ∈ N. En [15] Szczuka presenta algunos resultados que involucran al conjunto clN(P(a, x)) . Por ejemplo, en [15, Lema 3.3, p. 16] se muestra que si x 1 ≡ x (mód a), x 1 ≦ a y〈a, x〉= 1, entonces PG (a, x 1) ⊂ clN(PG (a, x)) . En [15, Lema 3.5, p. 16] se prueba que si a y x son impares y〈a, x〉= 1, entonces clN(PG (a, x)) = clN(PG (2a, x)) . En el Teorema 4.10 indicamos condiciones bajo las cuales PG (a, x) no es denso en (N, τG ). Como consecuencia del siguiente resultado, los múltiplos de a se encuentran en clN(PG (a, x)) .
Teorema 4.12. Sean a, x ∈ N tales que〈a, x〉= 1. Entonces, para cada n ∈ N, M(a) ⊂ clN(PG(an, x)) .
Demostración. Sea n ∈ N. Como〈a, x〉= 1, por el Teorema 2.4,〈an, x〉= 1. Tomemos ab ∈ M(a) y un abierto W en (N, τG ) de modo que ab ∈ W. Sea d ∈ N tal que〈d, ab〉= 1 y PG (d, ab) ⊂ W. Si〈d, an 〉≠ 1, entonces existe p ∈ P tal que p | d y p | an . Por el Teorema 2.6, p | a. Entonces p | d y p | ab, de donde〈d, ab〉≠ 1, una contradicción. Luego〈d, an 〉= 1 y, por consiguiente,〈d, an 〉| (ab−x). Esto implica, por el Teorema 4.7, que PG (d, ab) ∩ PG (an, x) ≠ ∅. Luego W ∩ PG (an, x) ≠ ∅ y, así, ab ∈ clN(PG (an, x)) . ☑
Corolario 4.13. Para cada d ∈ N, PG (1, d) es denso en (N, τG ).
Demostración. Sean d ∈ N y a = 1. Entonces〈a, d〉= 1, M(a) = N y, por el Teorema 4.12, N = M(a) ⊂ clN(PG (a, d)) , así que PG (a, d) = PG (1, d) es denso en (N, τG ). ☑
Por el Teorema 4.10 y el Corolario 4.13, entre los miembros BG algunos son densos en (N, τG), y otros no. Es un problema abierto el caracterizar los elementos de BG y los de la forma P(a, b), que son densos en (N, τG).
Teorema 4.14. Si a, b ∈ N, entonces PF (a, b) ∩ N ⊂ clN(P(a, b)) .
Demostración. Notemos que si b ≦ a, entonces por el Teorema 2.8, PF (a, b) ∩ N = P(a, b) ⊂ clN(P(a, b)) . Sea x ∈ PF (a, b) ∩ N. Entonces existe z ∈ Z tal que x = az + b. Sean U un abierto en (N, τG ) y c ∈ N tales que x ∈ U,〈c, x〉= 1 y PG (c, x) ⊂ U. Como〈c, a〉| a, sucede que〈c, a〉| az. Luego〈c, a〉| (x − b) y, por el Teorema 4.5, PG (c, x) ∩ P(a, b) = P(c, x) ∩ P(a, b) ≠ ∅. Esto prueba que x ∈ clN(P(a, b)) . ☑
Sean a, b ∈ N. Notemos que
En otras palabras, PF (a, b) ∩ N se consigue uniéndole a P(a, b), aquellos elementos de la progresión aritmética {b − a, b − 2a, b − 3a, . . .} que sean mayores o iguales a uno.
El siguiente resultado aparece en la parte 10. de [12, Ejemplos 60 y 61, p. 83]. La prueba que presentamos difiere de la dada en [12].
Teorema 4.15. Sean c ∈ N y p ∈ P tales que〈p, c〉= 1. Entonces, para cada n ∈ N, clN(PG(pn, c)) = M(p) ∪ [PF (pn, c) ∩ N].
Demostración. Tomemos n ∈ N. Como〈p, c〉= 1, por el Teorema 2.4,〈pn, c〉= 1. Por el Teorema 4.14, PF (pn, c) ∩ N ⊂ clN(PG (pn, c)) , y por el Teorema 4.12, M(p) ⊂ clN(PG (pn, c)) . Por tanto M(p) ∪ [PF (pn, c) ∩ N] ⊂ clN(PG (pn, c)) . Para probar la otra contención, sea x ∈ clN(PG (pn, c)) . Entonces x ∈ N y todo abierto básico en (N, τG ) que tiene a x, interseca a PG (pn, c). Luego,
Si p | x, entonces x ∈ M(p). Consideremos, por tanto, que p ∤ x. Sea t = pn . Notemos que〈pn, pn 〉= pn . Supongamos que〈t, x〉=〈pn, x〉≠ 1. Entonces existe q ∈ P tal que q | pn y q | x. Por el Teorema 2.6, q | p. Esto implica que q = p, por lo que p | x, un absurdo. Luego〈t, x〉=〈pn, x〉= 1 y, por (4), PG (pn, x) ∩ PG (pn, c) ≠ ∅. Aplicando el Teorema 4.7, deducimos que pn | (x−c), de donde x ∈ PF (pn, c)∩N. Con esto probamos que clN(PG (pn, c)) ⊂ M(p) ∪ [PF (pn, c) ∩ N]. ☑
Sean c ∈ N y p ∈ P tales que〈p, c〉= 1. Entonces, para cada n ∈ N tal que c < pn , por los Teoremas 2.8 y 4.15 tenemos que
Sean a, x ∈ N tales que〈a, x〉= 1. Es un problema abierto el describir el conjunto clN(PG (a, x)) . Por el Teorema 4.12, M(a) ∪ PG (a, x) ⊂ clN(PG (a, x)) . Sin embargo, describir a clN(PG (a, x)) \ (M(a) ∪ PG (a, x)) parece un problema difícil. Hasta donde se ha investigado, solo se conocen los resultados de Szczuka que hemos mencionado, los Teoremas 4.10, 4.12, 4.15 y el Corolario 4.13.
Teorema 4.16. Para cada d ∈ N, PG (1, d) es de Brown en (N, τG ). En particular, PG (1, d) es conexo.
Demostración. Sean U y V dos abiertos no vacíos en PG (1, d). Como PG (1, d) es abierto en (N, τG ), U y V son abiertos en (N, τG ). Sean x ∈ U y y ∈ V. Tomemos a, b ∈ N tales que〈a, x〉=〈b, y〉= 1, PG (a, x) ⊂ U y PG (b, y) ⊂ V. Si a = 1, entonces PG (a, x) = {x+n: n ∈ N0}. Como PG (b, y) es infinito, existe n 0 ∈ N0 tal que y+bn 0 ≧ x, y entonces
Por tanto, cl PG (1,d)(U) ∩ cl PG (1,d)(V ) ≠ ∅. De manera similar, si b = 1 tenemos que cl PG (1,d)(U)∩clPG (1,d)(V ) ≠ ∅. Ahora supongamos que a ≧ 2 y b ≧ 2. Por el Teorema 4.12, M(a) ⊂ clN(PG (a, x)) y M(b) ⊂ clN(PG (b, y)) . En particular, abd ∈ clN(PG (a, x)) ∩ clN(PG (b, y)) . Como a ≧ 2 y b ≧ 2, tenemos que d < abd, así que abd ∈ PG (1, d). Luego
Por tanto, cl PG (1,d)(U) ∩ cl PG (1,d)(V ) ≠ ∅ y, así, PG (1, d) es de Brown en (N, τG ). Como los espacios de Brown son conexos, PG (1, d) es conexo. ☑
A continuación presentamos una prueba explícita de lo que M. Brown afirmó en el resumen de la plática que impartió en abril de 1953, y que comentamos en la Introducción.
Teorema 4.17. (N, τG ) es de Brown. En particular, (N, τG ) es conexo y no es T 2½.
Demostración. Como PG (1, 1) = N, el resultado se sigue del Teorema 4.16 y del hecho de que los espacios de Brown son conexos y no T 2½. ☑
Sería interesante caracterizar los subconjuntos de (N, τG ) que son de Brown. En particular, caracterizar los conjuntos de la forma PG (a, b) y/o P(a, b) que son de Brown en (N, τG ). Como vimos en el Teorema 4.16, hay elementos de BG que son de Brown. En el Teorema 4.18 mostramos que también hay elementos de BG que no son de Brown.
Hemos demostrado que la conexidad del espacio (N, τG ) es consecuencia del hecho de que es de Brown. Existen otras propiedades que implican la conexidad. Por ejemplo, un espacio topológico X es hiperconexo si todo subconjunto abierto y no vacío de X, es denso en X. Decimos que X es ultraconexo si para cada x, y ∈ X con x ≠ y, se cumple que cl X ({x}) ∩ cl X ({y}) ≠ ∅. Si X es hiperconexo, entonces X no contiene dos subconjuntos abiertos, ajenos y no vacíos. Por otro lado, si X es ultraconexo, entonces X no es T 1 y, en consecuencia, tampoco T 2. Por lo tanto, todo espacio hiperconexo o ultraconexo es conexo pero no T 2. No es complicado ver que todo espacio hiperconexo o ultraconexo es de Brown. El recíproco de esta afirmación no es cierto, pues como hemos visto, (N, τG ) es de Brown y T 2, por lo que dicho espacio no es hiperconexo ni ultraconexo.
Por [4, Teoremas 3.1.9 y 3.3.1], los espacios compactos y T 2, así como los espacios localmente compactos y T 2, son T 4 y por tanto T 2½. Entonces (N, τG ) no es compacto ni localmente compacto. Estas observaciones también fueron hechas por Golomb en [7, Teorema 5] y [8, Teorema 5], aunque con demostraciones distintas a las que hemos presentado. Sería interesante determinar si (N, τG ) posee alguna propiedad de compacidad.
El siguiente resultado muestra que una buena cantidad de elementos de la forma PG (p, c), donde p ∈ P, no son conexos en (N, τG ). Hasta donde hemos investigado, el siguiente resultado aparece en la literatura por primera vez.
Teorema 4.18. Sean c ∈ N y p ∈ P con〈p, c〉= 1. Tomemos a, b ∈ PG (p, c) tales que a < b y n,m ∈ N0, de modo que a = pm+ c, b = pn + c y 0 ≦ m < n. Entonces
son abiertos en (N, τG ) y tales que a ∈ U, b ∈ V, U ∩ V = ∅ y PG (p, c) = U ∪ V. En particular, PG (p, c) no es conexo ni de Brown.
Demostración. Tomemos c, p, a, b, n y m como se indica en el teorema. Como p ∈ P y〈p, c〉= 1, el Teorema 2.7 garantiza que〈pn +1, pi + c〉= 1, para cada i ∈ N0. Entonces podemos considerar los conjuntos U y V que se indican en (5), y estos son abiertos en (N, τG ). La propiedad 1) del Teorema 3.1 asegura que U y V son conjuntos infinitos. Como 0 ≦ m < n < 2 n ≦ pn , tenemos que m+ 1 ≦ n ≦ pn − 1. Por tanto,
y
Es decir, a ∈ U y b ∈ V. Para verificar que U y V son ajenos, supongamos, por el contrario, que existe z ∈ U ∩ V. Sean i ∈ {0, 1, . . . ,m} y j ∈ {m+ 1,m+ 2, . . . , pn − 1} tales que z ∈ PG(pn +1, pi + c) y z ∈ PG(pn +1, pj + c). Como pn +1 > 1, pues p es un número primo, tenemos que
La transitividad de la congruencia y los incisos 1) y 3) del Teorema 2.10 implican que pi + c ≡ pj + c (mód pn +1), de donde pi ≡ pj (mód pn +1). Luego i ≡ j (mód pn). Sin embargo, como el conjunto A = {0, 1, . . . ,m,m+1, . . . , pn −1} es un sistema completo de residuos módulo pn , ningún par de elementos distintos de A son congruentes módulo pn . En particular, como i ≦ m < m+1 ≦ j, resulta que i ≢ j (mód pn ). De esta contradicción se infiere que U ∩ V = ∅.
Vamos a probar ahora que U ∪ V = PG (p, c). Si z ∈ U, entonces existe i ∈ {0, 1, . . . ,m} tal que z ∈ PG (pn +1, pi + c). Tomemos z 0 ∈ N0 de modo que z = pn +1 z 0 + pi + c. Entonces z = p(pnz 0 + i) + c ∈ PG (p, c). De manera similar, si z ∈ V, existe j ∈ {m+ 1,m+ 2, . . . , pn − 1} tal que z ∈ PG (pn +1, pj + c). Al tomar z 1 ∈ N0 de modo que z = pn +1 z 1 + pj + c, deducimos que z = p(pnz 1 + j) + c ∈ PG (p, c). Esto prueba que U ∪ V ⊂ PG (p, c).
Para probar la otra contención, sea z ∈ PG (p, c). Entonces existe k ∈ N0 para el cual z = pk + c. Por el Algoritmo de la División (Teorema 2.1) aplicado a k y pn , existen s, t ∈ N0 de manera que k = pns + t y 0 ≦ t < pn . Así obtenemos
Como 0 ≦ t < pn y 0 ≦ m < pn , se sigue que
Luego, de (6),
Esto prueba que PG (p, c) ⊂ U ∪V y, como la otra contención también es cierta, U ∪V = PG (p, c). Así probamos la primera parte del teorema. Ahora bien, como el conjunto PG (p, c) ha sido escrito como la unión de dos conjuntos abiertos en (N, τG ), que además son ajenos y no vacíos, PG (p, c) no es conexo. Como los espacios de Brown son conexos, PG (p, c) no es de Brown. ☑
Sean c ∈ N y p ∈ P tales que〈p, c〉= 1. Tomemos a, b ∈ PG (p, c) de modo que b < a. Usando las mismas ideas que mostramos en la prueba del Teorema 4.18, se sigue que existen abiertos U y V en (N, τG ) tales que a ∈ U, b ∈ V, U ∩ V = ∅ y PG (p, c) = U ∪ V. Tenemos, por tanto, el siguiente resultado.
Teorema 4.19. Sean c ∈ N y p ∈ P tales que〈p, c〉= 1. Tomemos a, b ∈ PG (p, c) de modo que a ≠ b. Entonces existen abiertos U y V en (N, τG ) tales que a ∈ U, b ∈ V, U ∩ V = ∅ y PG (p, c) = U ∪ V. En otras palabras, PG (p, c) está totalmente separado.
Como los espacios totalmente separados son hereditariamente disconexos, para cada c ∈ N y p ∈ P con〈p, c〉= 1 el conjunto PG(p, c) es hereditariamente disconexo. Utilizando esto, presentamos algunas consecuencias del Teorema 4.19. Como mencionamos en la Introducción, en 1969 Kirch probó que (N, τG) no es localmente conexo en 1. En el siguiente teorema generalizamos este resultado.
Teorema 4.20. Para ningún d ∈ N, PG (1, d) es conexo en pequeño, o bien casi conexo en pequeño en todos sus puntos.
Demostración. Sea d ∈ N y supongamos, por el contrario, que PG (1, d) es conexo en pequeño, o bien casi conexo en pequeño en algún punto c ∈ PG (1, d). Definimos un conjunto PG (p, c) como sigue: si c es impar, sea p = 2. Si c es par, tomamos p ∈ P tal que c < p. En cualquier caso, p ∈ P,〈p, c〉= 1 y PG (p, c) es un subconjunto abierto de PG (1, d) tal que c ∈ PG (p, c). Como PG (1, d) es conexo en pequeño o bien casi conexo en pequeño en c, existe un subconjunto conexo C de PG (1, d) tal que int PG(1,d)(C) ≠ ∅ y C ⊂ PG (p, c). Al ser PG (1, d) abierto en (N, τG ), tenemos que intN(C) ≠ ∅. Como los subconjuntos abiertos y no vacíos de (N, τG ) son infinitos, el conjunto C es infinito. Esto contradice el hecho de que PG (p, c) es hereditariamente disconexo. Por tanto, PG (1, d) no es conexo en pequeño ni casi conexo en pequeño en c. ☑
Corolario 4.21. (N, τG ) no es conexo en pequeño ni casi conexo en pequeño en ninguno de sus puntos. En particular (N, τG ) no es localmente conexo.
Demostración. Como PG (1, 1) = N, la primera parte se sigue del Teorema 4.20. Si (N, τG ) es localmente conexo, entonces (N, τG ) es conexo en pequeño en cada uno de sus puntos, lo cual contradice el Teorema 4.20. ☑
Hemos visto que la base BG posee elementos que son conexos, y también elementos que son hereditariamente disconexos. Sería interesante poder encontrar condiciones necesarias y suficientes bajo las cuales dos elementos de BG son homeomorfos. Incluso encontrar condiciones bajo las cuales un elemento de BG sea una imagen continua de otro elemento de BG .
Para a ∈ N, definimos Θ(a) = {p ∈ P: p | a}. Observemos que Θ(1) = ∅. El siguiente resultado aparece en [13, Teorema 3.3]. La prueba que presentamos es diferente, e incluso más corta, a la dada en el artículo [13], pues utilizamos el Teorema 4.19.
Teorema 4.22. Sean a, b ∈ N. Entonces P(a, b) es conexo en (N, τG ) si y sólo si Θ(a) ⊂ Θ(b). En particular,
1) M(a) es conexo en (N, τG );
2) si〈a, b〉= 1, entonces PG (a, b) es conexo en (N, τG ) si y sólo si a = 1.
Demostración. Supongamos que P(a, b) es conexo. Si Θ(a) no es un subconjunto de Θ(b), entonces a > 1 y existe p ∈ Θ(a) tal que p ∉ Θ(b). Luego p es un número primo que divide a a pero no a b. Por tanto,〈p, b〉= 1. Como p | a, tenemos que P(a, b) ⊂ PG(p, b). Del Teorema 4.19 se sigue que PG(p, b) es hereditariamente disconexo, así que P(a, b) posee solo un elemento, lo cual es una contradicción. Esto prueba que Θ(a) ⊂ Θ(b).
Ahora supongamos que Θ(a) ⊂ Θ(b). Si P(a, b) no es conexo, entonces existen dos subconjuntos no vacíos O 1 y O 2 de P(a, b), abiertos en el subespacio P(a, b) de (N, τG ) y tales que P(a, b) = O 1 ∪ O 2 y O 1 ∩ O 2 = ∅. Sean U 1 y U 2 abiertos en (N, τG ) tales que O 1 = U 1 ∩ P(a, b) y O 2 = U 2 ∩ P(a, b). Consideremos b 1 ∈ O 1 y b 2 ∈ O 2. Como b 1 ∈ U 1, b 2 ∈ U 2 y tanto U 1 como U 2 son abiertos en (N, τG ), existen a 1, a 2 ∈ N tales que〈a 1, b 1〉=〈a 2, b 2〉= 1, PG(a 1, b 1) ⊂ U 1 y PG(a 2, b 2) ⊂ U 2.
Vamos a probar que〈a, a 1〉= 1. Para esto, supongamos que〈a, a 1〉≠ 1. Entonces existe p ∈ P tal que p | a y p | a 1. Luego p ∈ Θ(a) y, como Θ(a) ⊂ Θ(b), tenemos que p ∈ Θ(b). Luego p | b y p | a 1. Ahora bien, como b 1 ∈ O 1 ⊂ P(a, b), existe n 1 ∈ N tal que b 1 = an 1 + b. En vista de que a y b son múltiplos de p, de la igualdad b 1 = an 1 + b, se sigue que p | b 1. Luego p | a 1 y p | b 1, de donde p |〈a 1, b 1〉, es decir p | 1. Esto es un absurdo, luego〈a, a 1〉= 1. De manera similar, se prueba que〈a, a 2〉= 1. Luego, por el Corolario 4.6,
Ahora vamos a probar que P(a, b) ∩ M(a 1) ⊂ O 1. Tomemos un elemento d ∈ P(a, b) ∩ M(a 1). Como P(a, b) = O 1 ∪ O 2, tenemos que d ∈ O 1 o bien d ∈ O 2. Supongamos que d ∈ O 2. Entonces d ∈ U 2 y, como U 2 es abierto en (N, τG ), existe c ∈ N tal que〈c, d〉= 1 y PG (c, d) ⊂ U 2. Si existe p ∈ P tal que p | c y p | a 1, entonces, como d es un múltiplo de a 1 y p | a 1, tenemos que p | d. Luego p | c y p | d, de donde p |〈c, d〉, es decir p | 1. Esto es absurdo, así que〈c, a 1〉= 1. Ahora supongamos que existe p ∈ P tal que p | a y p | c. Como Θ(a) ⊂ Θ(b) y p ∈ Θ(a), tenemos que p ∈ Θ(b). Luego p | b y, en vista de que d ∈ P(a, b) y tanto a como b son múltiplos de p, tenemos que p | d. Entonces p | c y p | d, de donde p |〈c, d〉. Así p | 1, lo cual es absurdo. Esto prueba que〈a, c〉= 1.
Notemos que a, c, y a 1 son números naturales tales que〈a 1, c〉=〈a 1, a〉=〈c, a〉= 1. Entonces, por el Teorema 4.8, PG(a 1, b 1) ∩ PG(c, d) ∩ P(a, b) ≠ ∅. Esto implica que
Luego O 1 ∩ O 2 ≠ ∅, lo cual es una contradicción. Entonces d ∈ O 1, probando con esto que P(a, b)∩M(a 1) ⊂ O 1. De manera similar se prueba que P(a, b)∩M(a 2) ⊂ O 2. Como〈a, a 1〉=〈a, a 2〉= 1, por el Teorema 2.4, ha, a 1 a 2 i = 1. Luego, por el Corolario 4.6, P(a, b) ∩M(a 1 a 2) ≠ ∅. Ahora bien, notemos que
Esto contradice el hecho de que O 1 ∩ O 2 = ∅. Dicha contradicción proviene de suponer que P(a, b) no es conexo. Por tanto, P(a, b) es conexo.
Para probar 1), notemos que M(a) = P(a, a) y, como Θ(a) ⊂ Θ(a), por la primera parte del teorema M(a) es conexo en (N, τG ).
Para probar 2) supongamos primero que〈a, b〉= 1 y que PG(a, b) es conexo. Entonces, por la primera parte del teorema, Θ(a) ⊂ Θ(b). Si a ≧ 2, entonces existe p ∈ P tal que p | a, por lo que también p | b, contradiciendo que〈a, b〉= 1. Luego a = 1. El recíproco se sigue del Teorema 4.16. ☑
A continuación presentamos un resultado que pertenece a la Teoría Analítica de Números, y es llamado el Teorema de Dirichlet.
Teorema 4.23. Sean a, b ∈ N con a > 1 y〈a, b〉= 1. Entonces existe una cantidad infinita de números primos p, para los cuales p ≡ b (mód a).
La prueba del Teorema de Dirichlet utiliza propiedades de ciertas funciones multiplicativas, y varios resultados sobre aritmética de números complejos. En vista de que es bastante dispendiosa, no suele incluirse en textos clásicos de Teoría de Números. Una prueba detallada se puede consultar en [1, Sección 7.3, p. 148].
Sean a, b ∈ N con a > 1 y〈a, b〉= 1. Tomemos p ∈ P. Notemos que p ≡ b (mód a) si y sólo si p ∈ PF (a, b) ∩ P. Por tanto, en términos de los elementos de la base BF de τF el Teorema de Dirichlet dice que si a, b ∈ N son tales que a > 1 y〈a, b〉= 1, entonces el conjunto PF (a, b) ∩ P es infinito. Si a = 1, entonces PF (a, b) ∩ P es infinito, pues PF (a, b) = PF (1, b) = Z y, por tanto, PF (a, b)∩P = P es infinito (Teorema 4.3). Tenemos entonces que
Utilizaremos (⋆) para probar que, en el espacio (Z, τF ), la cerradura del conjunto P0 = {±p: p ∈ P} es P0 ∪ {−1, 1}. Los elementos de P0 se llaman enteros primos.
Teorema 4.24. cl(Z, τF )(P0) = P0 ∪ {−1, 1}.
Demostración. Sea b ∈ Z \ {−1, 0, 1}. Hagamos a = 2|b|, donde |b| es el valor absoluto de b. Entonces |b| = b si b ≧ 0, mientras que |b| = −b si b < 0. Por esta razón, podemos decir que |b| = ±b. Ahora bien, x ∈ PF (a, b) si y sólo si existe n ∈ Z tal que
Como b ∈ Z \ {−1, 0, 1}, el producto b(1±2n) es un entero primo si y sólo si n = 0, caso en el cual dicho número coincide con b. Por tanto,
Esto muestra que si b ∈ Z \ {−1, 0, 1} y, además, b ∉ P0, entonces PF (2|b|, b) es un abierto en (Z, τF ) que tiene a b y no interseca a P0. Luego, b ∉ cl(Z, τF )(P0). Naturalmente P0 ⊂ cl(Z, τF )(P0), por lo que, para determinar cl(Z,τF )(P0), solo debemos verificar si contiene los enteros −1, 0 y 1. Notemos que PF (4, 0) es un abierto en (Z, τF ) que tiene a 0. Como PF (4, 0) = {4z: z ∈ Z} es el conjunto de los enteros que son múltiplos de 4, resulta que PF (4, 0)∩P0 = ∅. Luego 0 ∉ cl(Z,τF )(P0). Consideremos ahora un abierto U en (Z, τF ) tal que 1 ∈ U. Entonces existe c ∈ N tal que PF (c, 1) ⊂ U. Como〈c, 1〉= 1, por (⋆) PF (c, 1) ∩ P ≠ ∅. En particular U ∩ P0 ≠ ∅. Esto prueba que 1 ∈ cl(Z,τF )(P0). De manera similar se prueba que −1 ∈ cl(Z,τF )(P0). Por consiguiente, cl(Z,τF )(P0) = P0∪{−1, 1}. ☑
Corolario 4.25. cl(Z,τF )(P) = P ∪ {−1, 1} y cl(N,(τF )N)(P) = P ∪ {1}, donde (τF )N es la topología relativa de (Z, τF ) a N.
Demostración. Como P ⊂ P0, por el Teorema 4.24,
Por tanto, para determinar cl(Z,τF )(P), debemos verificar si contiene los enteros −1, 1 y los de la forma −p, donde p ∈ P. Sea U un abierto en (Z, τF ) tal que 1 ∈ U. Entonces existe c ∈ N tal que PF (c, 1) ⊂ U. Como〈c, 1〉= 1, por (⋆) PF (c, 1) ∩ P ≠ ∅. En particular, U ∩ P ≠ ∅. Esto prueba que 1 ∈ cl(Z,τF )(P). De manera similar se prueba que −1 ∈ cl(Z,τF )(P). Supongamos ahora que p ∈ P. Notemos que x ∈ PF (3p,−p) si y sólo si existe n ∈ Z tal que x = 3pn − p = p(3n − 1). Como p ∈ P para ningún n ∈ Z, el producto p(3n − 1) es un número primo. Por tanto, PF (3p,−p) es un abierto en (Z, τF ) tal que −p ∈ PF (3p,−p) y PF (3p,−p)∩P = ∅. Luego, −p ∉ cl(Z,τF )(P). Esto prueba que cl(Z,τF )(P) = P ∪ {−1, 1}. Para probar la segunda parte, notemos que
En el Corolario 4.25 indicamos que la cerradura de P en el espacio (N, (τF )N) es P ∪ {1}, por lo que P no es denso en (N, (τF )N). Como mostramos en el Teorema 4.28, P es denso en (N, τG ). Para probar esto necesitamos unos resultados previos.
Teorema 4.26. Las siguientes afirmaciones son equivalentes:
1) para cada PG (a, b) ∈ BG , PG (a, b) ∩ P es infinito;
2) para cada PG (a, b) ∈ BG , existe n ∈ N tal que an + b ∈ P.
Demostración. Es claro que 1) implica 2). Supongamos ahora que 2) se cumple. Sea PG (a, b) ∈ BG . Por 2), existe n 1 ∈ N tal que an 1+b ∈ P. Como a < an 1+b y an 1+b ∈ P, por el Teorema 2.5〈a, an 1+b〉= 1. Entonces PG (a, an 1+b) ∈ BG y, por 2), existe n 2 ∈ N tal que an 2+(an 1+b) = a(n 2+n 1)+b ∈ P. Entonces PG (a, b) contiene por lo menos dos números primos, a saber an 1+b y a(n 2+n 1)+b. Como a < a(n 2+n 1)+b y a(n 2+n 1)+b ∈ P, por el Teorema 2.5〈a, a(n 2 + n 1) + b〉= 1. Por tanto, PG (a, a(n 2 + n 1) + b) ∈ BG y, por 2), existe n 3 ∈ N tal que an 3 + a(n 2 + n 1) + b = a(n 3 + n 2 + n 1) + b ∈ P. Entonces PG (a, b) contiene por lo menos tres números primos, a saber an 1, a(n 2+n 1)+b y a(n 3 + n 2 + n 1) + b. Continuando de esta manera, resulta que el conjunto PG (a, b) contiene una cantidad infinita de números primos. Esto muestra que 2) implica 1). ☑
El Teorema de Dirichlet (Teorema 4.23) se puede enunciar en términos de elementos de la base BG . Dado PG (a, b) ∈ BG , con a > 1, el Teorema de Dirichlet asegura que PG(a, b) contiene una cantidad infinita de números primos. Si a = 1 y b ∈ N, entonces〈a, b〉= 1 y PG (a, b) = {b, b + 1, b + 2, . . .} contiene una cantidad infinita de números primos. Por tanto, para cada PG (a, b) ∈ BG se tiene que PG (a, b) contiene una cantidad infinita de números primos. Con esta observación será más práctico probar la siguiente equivalencia.
Teorema 4.27. El Teorema de Dirichlet es equivalente a afirmar que P es denso en (N, τG ).
Demostración. Supongamos que el Teorema de Dirichlet es cierto. Para ver que P es denso en (N, τG ), sea U un abierto no vacío en (N, τG ). Tomemos b ∈ U y a ∈ N de modo que〈a, b〉= 1 y PG (a, b) ⊂ U. Como el Teorema de Dirichlet es válido, PG (a, b) contiene una cantidad infinita de números primos. En particular PG (a, b) ∩ P ≠ ∅. Luego U ∩ P ≠ ∅. Esto prueba que P es denso en (N, τG ).
Ahora supongamos que P es denso en (N, τG ). Sean PG (a, b) ∈ BG y c ∈ PG (a, b) tales que c ≠ b. Por la parte 2) del Teorema 3.1,〈a, c〉= 1 y PG (a, c) ⊂ PG (a, b). Como PG (a, c) es un abierto no vacío en (N, τG ) y P es denso en (N, τG ), sucede que PG (a, c) ∩ P ≠ ∅. Esto implica que existe n ∈ N tal que an+b ∈ P y, por el Teorema 4.26, PG (a, b) contiene una cantidad infinita de números primos. Por tanto, el Teorema de Dirichlet se cumple. ☑
El Teorema 4.27 indica que una afirmación aritmética (el Teorema de Dirichlet, en este caso) es equivalente a una afirmación topológica (que P es denso en (N, τG )). Como el Teorema de Dirichlet es cierto, por el Teorema 4.27, tenemos el siguiente resultado.
Teorema 4.28. P es denso en (N, τG ).
Si podemos probar el Teorema 4.28, sin utilizar el Teorema de Dirichlet, posiblemente usando solamente argumentos topológicos, entonces por el Teorema 4.27 tendremos una demostración, en este caso topológica, del Teorema de Dirichlet. Como ya indicamos, la prueba que se conoce del Teorema de Dirichlet es compleja, por lo que resulta interesante saber si se pueden dar demostraciones alternativas y menos complicadas. Tanto en [7] como en [8], Golomb pregunta si es posible probar el Teorema 4.28, sin utilizar el Teorema de Dirichlet. Hasta donde sabemos, el problema permanece abierto.
El siguiente resultado asegura que P tiene interior vacío. En particular, P no es abierto en (N, τG ).
Teorema 4.29. No existe un abierto no vacío U en (N, τG ) tal que U ⊂ P.
Demostración. Supongamos que existe un abierto no vacío U en (N, τG ) tal que U ⊂ P. Tomemos b ∈ U y a ∈ N de manera que〈a, b〉= 1 y PG (a, b) ⊂ U. Entonces cada miembro de PG (a, b) es un número primo. En particular, b ≧ 2 y el elemento a(a + b + 1) + b, de PG (a, b), es primo. Sin embargo, como a + 1 ≧ 2, a + b ≧ 3 y
así, el número a(a + b + 1) + b es compuesto. De esta contradicción deducimos que no existe un abierto no vacío U en (N, τG ) tal que U ⊂ P. ☑
Un espacio topológico X es homogéneo si para cada x, y ∈ X existe un homeomorfismo f: X → X tal que f(x) = y. Es un problema abierto el determinar si (N, τG ) es homogéneo.




![Theorem of Dirichlet on F q [t]](/img/pt/prev.gif)