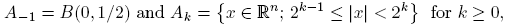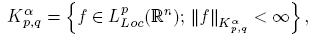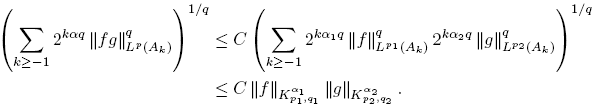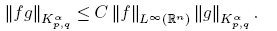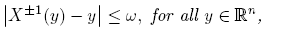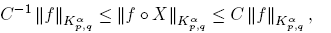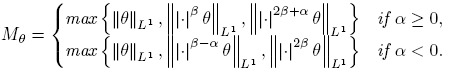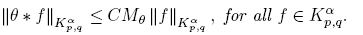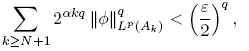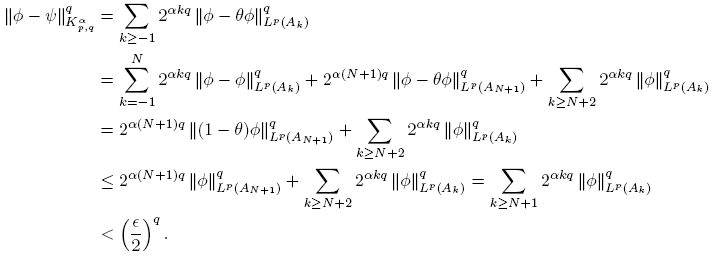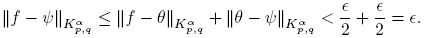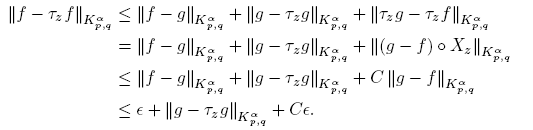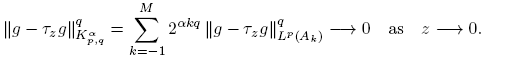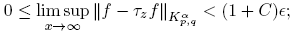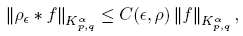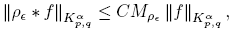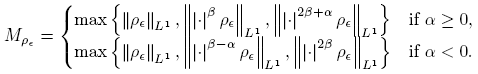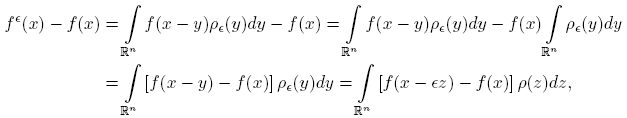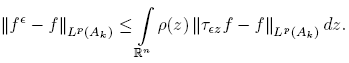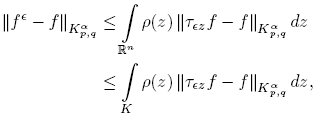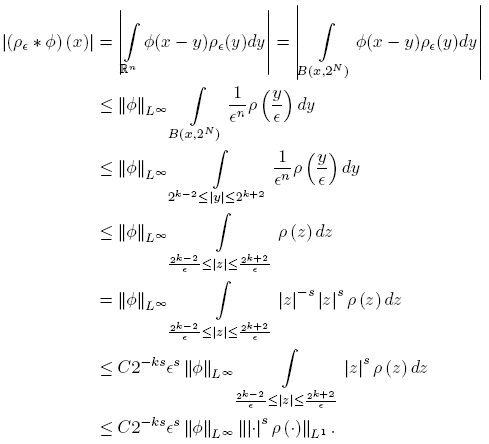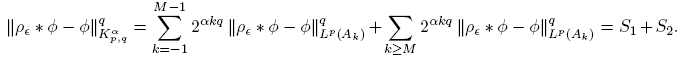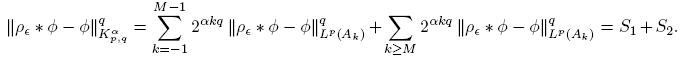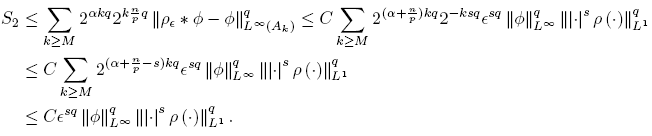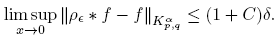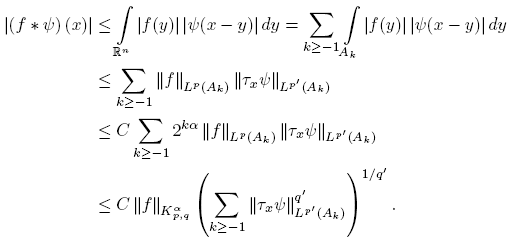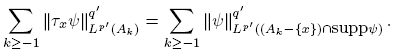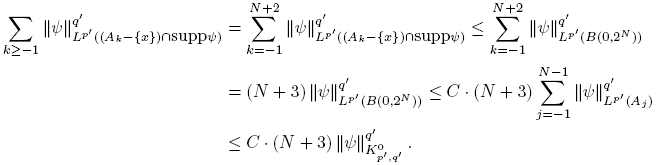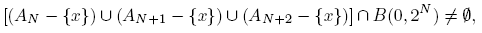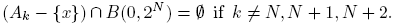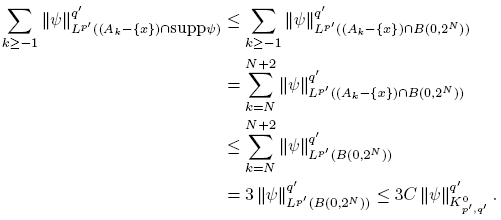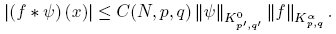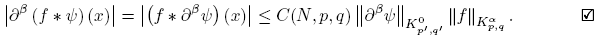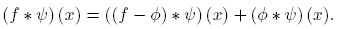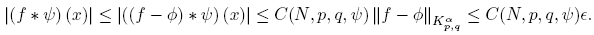1. Introduction
The Herz space Kα p,q was introduced by Herz [7] as a suitable environment for the image of the Fourier transform acting on a class of Lipschitz spaces, in order to obtain a Bernstein type theorem. A characterization of the Kα p,q -norm in terms of Lp -norms over annuli was given in [8] (see Definition 2.1). Recently, some versions of classical spaces based on Herz spaces Kα p,q , such as Hardy-Herz, Sobolev-Herz and Triebel-Lizorkin-Herz spaces, have presented an increasing interest in the literature of function spaces and turned out to be a useful tool in harmonic analysis (see [1],[4],[5],[10] and references therein). We also refer the reader to [9] for results of well-posedness of the Navier-Stokes equations in weak-Herz spaces, and to [3] for results of well-posedness of the Euler equations on Besov-Herz spaces.
In this paper we consider the Herz spaces Kαp,q, which are a natural generalization of the Lebesgue spaces Lp . We prove some approximation properties such as density of the spaces C ∞ c (R n ), continuity of the translation, continuity of the mollification, global behavior of the convolution with smooth functions, among others. This results generalize the corresponding ones in Lp . They seem necessary for the study of the transport equations as done in [2] in the frame work of the Lp spaces.
This paper is organized as follows. In Section 2 we recall the definition of the Herz spaces Kα p,q and some basic properties. Section 3 is devoted to the new results about approximation and global behavior of functions in Herz spaces and his convolution with smooth functions.
2. Herz spaces
This section is devoted to recall the definition of Herz spaces and establish some of their properties, which will be useful in the remainder of the paper.
For k integer and k ≥ −1, let Ak be defined as
where B(x 0,R) = {x ∈ R n ; |x − x 0| < R}. Then we have the disjoint decomposition R n = ∪ k≥−1 Ak .
Definition 2.1. Let 1 ≤ p,q ≤ ∞ and α ∈ R. The Herz space Kα p,q = Kα p,q (R n ) is defined by
where
In the case p = 1, we consider Kα
p,q
as a space of signed measures, with ║f║L¹(Ak) denoting the total variation of f on Ak
. The pair 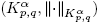 is a Banach space for α ∈ R, 1 ≤ p < ∞ and 1 ≤ q ≤ ∞ (see e.g. [6]). Also, note that K
0
p,1 → Lp
= K
0
p,p
→ K
0
p,∞. So, all the results presented here are a generalization of the corresponding results in Lp
. There is a version of Hölder’s inequality in Herz spaces (see [9]). In fact, let 1 ≤ p, p
1, p
2, q, q
1, q
2 ≤ ∞ and α, α
1, α
2 ∈ R be such that
is a Banach space for α ∈ R, 1 ≤ p < ∞ and 1 ≤ q ≤ ∞ (see e.g. [6]). Also, note that K
0
p,1 → Lp
= K
0
p,p
→ K
0
p,∞. So, all the results presented here are a generalization of the corresponding results in Lp
. There is a version of Hölder’s inequality in Herz spaces (see [9]). In fact, let 1 ≤ p, p
1, p
2, q, q
1, q
2 ≤ ∞ and α, α
1, α
2 ∈ R be such that 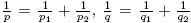 , and α = α
1 + α
2. Then,
, and α = α
1 + α
2. Then,
In particular,
The following result provides a control in Kα p,q -spaces for the action of a volume preserving diffeomorphism. Recall that a diffeomorphism X is volume preserving if for all measurable set Ω, we have μ(Ω) = μ(X(Ω)), where μ represent the Lebesgue measure.
Lemma 2.2 ([3]). Let 1 ≤ p, q ≤ ∞ and α ≥ 0. Let X: R n → R n be a volume-preserving diffeomorphism such that, for some fixed ω > 0,
where |·| stands for the Euclidean norm in R n. Then, there exists C > 0 such that
for all f ∈ Kα p,q .
The next lemma is key in order to prove the new results in Section 3. It provides an estimate for convolution operators in Herz spaces depending on certain weighted norms of the kernel θ.
Lemma 2.3 ([3]). (Convolution). Let α ∈ R and 1 ≤ p, q ≤ ∞. Let θ ∈ L 1 be such that Mθ < ∞ for some β > 0, where
Then, there is a constant C > 0 (independent of θ) such that
To finish this section we present a first result of density in Herz spaces.
Lemma 2.4 ([3]). Let 1 ≤ p,q ≤ ∞ and α ∈ R . Then, Schwartz space S is continuously included in Kα p,q. Moreover, the inclusion is dense provided that 1 ≤ p,q < ∞.
3. New results
Now we present some new results about approximation of functions in Herz spaces and global behavior of their convolution with smooth functions. This results can be useful in order to analyze the well-posedness of some PDEs in the framework of Herz spaces.
In what follows, let ρ ∈ S such that 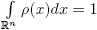 . For ∊ > 0 we define
. For ∊ > 0 we define 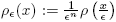 , additionally, for a mensurable function f ∈ Rn → R we also define f∊ (x) = (ρ∊ ∗ f) (x).
, additionally, for a mensurable function f ∈ Rn → R we also define f∊ (x) = (ρ∊ ∗ f) (x).
We first show that not only S but also C ∞ c (R n ) are dense in Herz spaces.
Theorem 3.1. Let 1 ≤ p,q < ∞ and α ∈ R. Then, the space C ∞ c (R n ) is dense in Kα p,q .
Proof. From Lemma 2.4 it follows that S is dense in Kα
p,q
. Let f ∈ Kα
p,q, ∊ > 0 and φ ∈ S such that 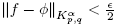 . Now, let N ∈ N such that
. Now, let N ∈ N such that
and let θ ∈ C ∞ c (R n ) be such that 0 ≤ θ ≤ 1, θ = 1 in B (0, 2 N ) and θ = 0 in [B (0, 2 N )] c . Defining ψ = θφ, we have that ψ ∈ C ∞ c (R n ), ψ = φ in B (0, 2 N ) and θ = 0 in [B (0, 2 N )] c . Moreover, it follows that
Thus,
Since ∊ > 0 is arbitrary, we conclude the proof. ☑
Now we prove the continuity of the translation mapping in Herz spaces.
Theorem 3.2. Let 1 ≤ p,q < ∞ and α ∈ R. Then, τzf → f in Kα p,q as z → 0 for all f ∈ Kα p,q. Here τzf denotes the mapping such that τzf(x) = f(x − z).
Proof. Note that, for |z| < 1, we have that the volume preserving diffeomorphism Xz
(x) = x − z trivially verifies ║Xz
− Id║∞ ≤ 1. Now, let f ∈
Kα
p,q
, ∞ > 0 and g
∈ C
∞
c
(R
n
) such that 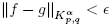 . Using Lemma 2.2, it follows that
. Using Lemma 2.2, it follows that
Now we prove that 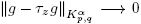 when z → 0. In fact, if |z| < 1, then suppg and suppτzg are contained in a common compact set K. Choosing M ∈ N such that K ⊂ B (0, 2
M
), and using that τzg → g in Lp
(R
n
) , we have that
when z → 0. In fact, if |z| < 1, then suppg and suppτzg are contained in a common compact set K. Choosing M ∈ N such that K ⊂ B (0, 2
M
), and using that τzg → g in Lp
(R
n
) , we have that
Thus, taking lim sup as z → 0 in (9) and using (10) we obtain
since ∊ > 0 is arbitrary, we obtain the result. ☑
Lemma 3.3. Let 1 ≤ p,q < ∞, α ∈ R, f ∈ Kα p,q and ρ ∈ S. Then,
where 0 < C(∊, ρ) ≤ C˜ (ρ) if 0 < ∊ < 1.
Proof. Using Lemma 2.3 we have that
where
Moreover, if 0 < ∊ < 1 is easy to see that Mρ∊ ≤ Mρ . ☑
Now we show the continuity of the mollification of a function in Herz spaces when the mollifier is in C ∞ c (R n ).
Theorem 3.4. Let f ∈ Kα p,q with 1 ≤ p,q < ∞, α ∈ R and ρ ∈ C ∞ c (R n ). Then, f∊ → f in Kα p,q as ∊ → 0.
Proof. By definition we have that
where we use the change y = ∊z. Now, using Minkowski’s inequality we get
Thus, using again Minkowski’s inequality (for sequences) we obtain
where suppρ = K. Since K is compact, we have that |z| < C
2 for all z ∈ K; moreover, for 0 < ∊ ≪ 1 we also have that |∊z| < 1 for all z ∈ K. Thus, using Lemma 2.2 we have that 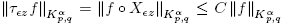 and it follows that
and it follows that 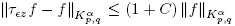 . Then, using (11), Proposition 3.2 and the Dominate Convergence Theorem we obtain the result. ☑
. Then, using (11), Proposition 3.2 and the Dominate Convergence Theorem we obtain the result. ☑
The following is an auxiliary lemma.
Proposition 3.5. Let φ ∈ C ∞ c (R n ), 1 ≤ p,q ≤ ∞, α ∈ R and ρ ∈ S. Then, φ∊ → φ in Kα p,q as ∊ → 0.
Proof. Let N ∈ N such that suppφ ⊂ B(0, 2 N ), and let M > N + 2. For k ≥ M and x ∈ Ak we have that
Thus, for any s > 0 we get
On the other hand,
Is clear that S 1 → 0 as ∊ → 0, because ρ∊ ∗ φ → φ in Lp (Ak ). For S 2, using the Hölder inequality, (12) and taking s > 0 large enough, we have
Then, S 2 → 0 as ∊ → 0. The estimates for S 1 and S 2 give the result. ☑
Now we prove the continuity of the mollification of a functions in Herz spaces when the mollifier is in S.
Theorem 3.6. Let f ∈ Kα p,q with 1 ≤ p,q < ∞, α ∈ R and ρ ∈ S. Then, f∊ → f in Kα p,q as ∊ → 0.
Proof. Let δ > 0 and φ ∈ C
∞
c
(R
n
) such that 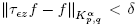 . For 0 < ∊ ≪ 1, we have
. For 0 < ∊ ≪ 1, we have
Taking ∊ → 0 and using Lemma 3.5, we obtain
Since δ > 0 was arbitrary, we prove the proposition. ☑
The following two results are related to the global behavior of convolutions of functions in Herz spaces with smooth functions.
Theorem 3.7.
Let 1 ≤ p, q ≤ ∞, α ≥ 0, f ∈ Kα
p,q and ψ ∈ C
∞
c
. Then f ∗ ψ ∈ C
∞ (R
n
) and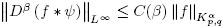 for all β multi-index.
for all β multi-index.
Proof. Note that f ∗ ψ ∈ C ∞ (R n ) follows from the fact that f ∈ L 1 loc and the classic theory of convolution. On the other hand, by definition we have
Let N ∈ N such that suppψ ⊂ B(0, 2 N ), and note that
Thus, if |x| ≤ 2 N+1, then (Ak−{x})∩suppψ = ∅ for k ≥ N +3; therefore, for |x| ≤ 2 N+1 we have
On the other hand, if |x| > 2 N+1, it follows that,
and
Then,
Thus, for any x ∈ R n we obtain
Similarly, for any x ∈ R n we have
Theorem 3.8. Let 1 ≤ p,q < ∞, α ≥ 0, f ∈ Kα p,q and ψ ∈ C ∞ c (R n ). Then f ∗ ψ ∈ C ∞ 0 (R n ) .
Proof. Let ∊ > 0 and φ ∈ C
∞
c
(R
n
) such that 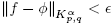 . Then,
. Then,
Since φ, ψ ∈ C ∞ c (R n ), we have that φ∗ψ ∈ C ∞ c (R n ); thus, |x| > C = C(∊), and we have that (φ ∗ ψ) (x) = 0. Therefore, for x large enough, it follows that
Now, proceeding as in the proof of the Theorem 3.7, we get
Since ∊ > 0 is arbitrary, we get the result. ☑