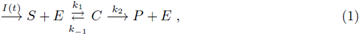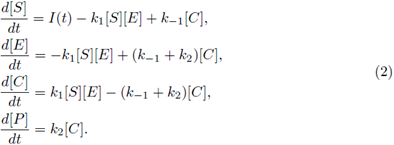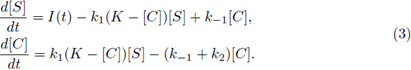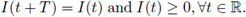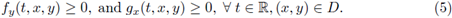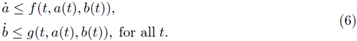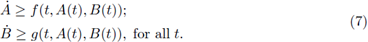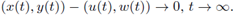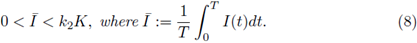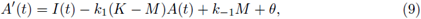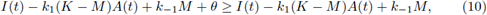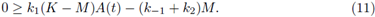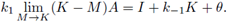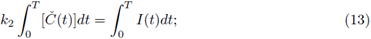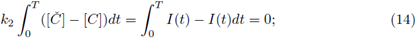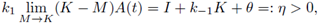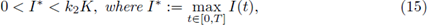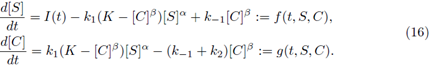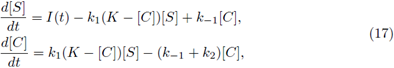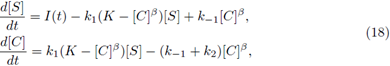1. Introduction
Mathematical models have become important tools in analyzing chemical reactions; of special interest are enzymatic reactions in biochemical systems. Enzymes are important in regulating biological processes acting as activators or inhibitors in a reaction. A basic scheme for a catalyzed reaction is based into the Michaelis-Menten equation, which is fundamental for enzyme kinetics. It can be described by the following kinetic mechanism:
where E denotes enzyme, S denotes substrate, P denotes product and C denotes enzyme substrate complex. I(t) is the rate of input of the substrate into the system. Letting [A] denote concentration of a chemical specie A. A well-studied law of action kinetic is the law of mass action; it assumes that the rate of a reaction is proportional to the concentrations of its reactants; the law of mass action leads to the system of following non-linear reaction equations:
All of the parameters are positive constants. Since the scheme (1) is reversible, then, by adding the second and third equations in the system (2), we have ([E] + [C])’ = 0; therefore [E] + [C] = K for all time t for some positive constant K. Using this relation, and since the last equation in system (2) decouples from the other equations, we can reduce model (2) to a two-dimensional system in terms of [S] and [C], as follows:
In chemical engineering it is common to use stirred tank reactors where fresh nutrient are supplied at periodic rate from external sources; on the other hand, a natural situation in biological system is that the rate of input of the substrate I fluctuates in periodic form; this is due to intrinsic oscillations in living organisms. So, for the interest of the chemical industry or for biological reasons of the reactions considered, we can assume that I is a non negative, non constant continuous I-periodic function;
In the study of enzymatic models the analysis of periodic solutions is seen as an important goal, since this periodicity reveals the recurrence of biochemical rhythms of living organisms. Hence, determining existence of such solutions under different parameter configurations and input functions is crucial.
Stoleriu and coworkers [5] studied the existence of periodic solutions in a particular class of input rate I, by using Brouwer's fixed-point theorem. Katriel [1] proved the existence of periodic orbits of (3), by using Leray-Schauder degree theory. Moreover, he asked if that periodic solution is unique and asymptotically stable. Using the theory of cooperative systems, in the sequel we will recover Katriel's result as an application of our main result; moreover, we obtain the uniqueness of such orbit, and that the periodic solution attracts all other positive solutions, answering affirmatively to Katriel's questions [1]. On the other hand, considering the generalized mass-action law we obtain more general systems of type (3); for that kind of systems we also prove the existence of periodic orbits.
2. Results
We first review the cooperative systems (this material is included for completeness and to fix some of the notation); for a brief introduction to cooperative systems see [4]. For two points x, y ∈ ℝn denote the partial order u ≤ v, if ui ≤ vi for each i; also denote u < v if u ≤ v and u ≠ v. Consider a system
where f,g are C1 in an open D ⊂ ℝ2 and continuous T-periodic functions on t. Recall that (4) is said a cooperative system in ℝ x D if
The cooperative systems have very important properties. For example: the monotonicity of the local flow generated by (4).
We say that a pair of T-periodic differentiable functions (a(t),b(t)) is a subsolution pair of (4) if
Analogously, a pair of T-periodic differentiable functions (A(t), B(t)) is a supersolution pair if
We say that sub-and supersolution pairs are ordered if for all t we have a(t) < A(t) and
Finally, we say that a solution (u(t), w(t)) of (4) is globally attracting on a positively invariant set R ⊆ ℝ2 if all solutions (x(t),y(t)) with (x(0),y(0)) ∈ R satisfy
An important feature for the cooperative system (4) about periodic orbits was established in [2], Theorem 2.1. More precisely, the following result holds.
Theorem 2.1. Assume that the system (4) is cooperative and has ordered sub- and super-solution pairs (a(t),b(t)) and (A(t), B(t)). Then the system has a T-periodic solution, satisfying a(t) < x(t) < A(t),b(t) < x(t) < B(t), ∀t. Furthermore, any solution of (4), with the initial (x(0), y(0)) ∈ (a(0),A(0)) x (b(0), B(0)), converges to the product
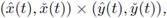 where
where
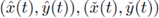 are the minimal, maximal T-periodic solution, respectively.
are the minimal, maximal T-periodic solution, respectively.
Now we state our first result
Theorem 2.2. Assume k 1 , k 2 , k -1 , K > 0, and I(t) is a non negative, non constant continuous T-periodic function. Then we get:
i) There is at least one T-periodic solution [S(t)], [C(t)] of (3) whose components are positive if, and only if,
ii) Under (8) the T-periodic solution is unique in
iii) It attracts all other positive solutions of (3), when t → ∞.
Proof. i) It is clear that (8) is a necessary condition for the existence of a T-periodic solution. In fact by adding both equations in (3) and integrating the result on [0,T]. Now assume the condition (8); first, note that system (3) is of cooperating type, so to use Theorem 2.1 we need construct sub- and super-solution pairs. First we take (a(t), b(t)) = (0, 0), which is a subsolution pair.
For the super-solution pair we take A(t) to be the unique positive T-periodic solution of
with θ and M < K positive constants to be fixed later. Also we take B(t) = M. To obtain that (A(t), B(t)) are a supersolution pair, it must be fulfilled that
And
Now, the periodic solutions A(t) of (9) (as function of M) satisfy
Taking the limit M → K in the right side of (11) we get
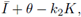 which is negative by (8) for θ sufficiently small; therefore, the inequality (11) is satisfied for θ small and M close to K. Thus we have sub- and super-solution pairs; then, by Theorem 2.1. there is at least one T-periodic solution, which proves i).
which is negative by (8) for θ sufficiently small; therefore, the inequality (11) is satisfied for θ small and M close to K. Thus we have sub- and super-solution pairs; then, by Theorem 2.1. there is at least one T-periodic solution, which proves i).
ii) By adding both equations in (3) and integrating for a periodic solution we get
this is also true for the maximal periodic solution
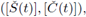 i.e.,
i.e.,
thus, from (12) and (13) we have
therefore for any periodic solution we have
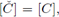 but from the second equation in (3) we obtain that
but from the second equation in (3) we obtain that
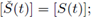 this establishes the uniqueness.
this establishes the uniqueness.
iii) Note that the band (0,K) is attractor to (3) in ℝ2, and by Theorem 2.1 there is a unique periodic solution in (0,A(0)) x (0,K) which is attractor in this set, where A is the unique periodic solution of (9). Since
then A(0) becomes arbitrarily large. Then the periodic solution is globally attracting on all positive solutions of (3), when t → ∞
As we have really mentioned Katriel [1] proved the existence of periodic orbits of (3) under the condition (8), by using Leray-Schauder degree theory. Moreover, he proposed the next question: is it true that if
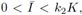 the periodic solution is unique and globally stable? From our result we obtain a different proof of existence, and we answer affirmatively his questions.
the periodic solution is unique and globally stable? From our result we obtain a different proof of existence, and we answer affirmatively his questions.
It should be noted that the existence of periodic orbits in the particular case of I(t): = I 0 (1 + є sin(wt)) was considered in [5] by using Brouwer's fixed-point theorem. Observe that Theorem 2.2 gives an alternative proof to Theorem 1 in [5], which we remember below.
Corollary 2.3. Let I(t): = I 0 (1 + є sin(wt)), with 0 ≤ є ≤ 1. If
then for any value of є, 0 ≤ є ≤ 1, the system (3) has at least one positive
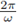 -periodic solution. Moreover, the periodic solution /or e sufficiently small is unique.
-periodic solution. Moreover, the periodic solution /or e sufficiently small is unique.
Note that the condition (15) implies (8), but it is a stronger condition; moreover, we do not require additional conditions for uniqueness (over є), therefore Theorem 2.2 produces a slight generalization of this result.
To model the dynamics of the concentrations of the chemical species involved, we also can consider the generalized mass-action law (see [3]). Under this law we obtain a more general enzyme catalysed system than (3), written as
All of the parameters (exponents included) are positive constants and I is a non constant continuous T-periodic function.
With a similar proof as in Theorem 2.2, we obtain the following slight generalization of this result:
Theorem 2.4. Assume k 1 , k 2 , k -1 , K > 0, and I(t) is a non negative, non constant continuous T -periodic function. If β > 0 and α = 1, then we get:
i) There is at least one T-periodic solution [S(t)], [C(t)] of (16) whose components are positive if, and only if, (8) holds.
ii) Under (8) the T-periodic solution is unique in
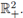
iii) It attracts all other positive solutions of (16), as t → ∞.
2.1. Examples
In the previous section we established analytically the existence of periodic solutions for system (2) of enzymatic reactions. The object of this section is to show numerical evidence of the existence of periodic solutions. We numerically solved these equations using a 4th order accurate Runge-Kutta integrator, which was programmed in FORTRAN 95. The graphs correspond to numerical approximations of the periodic analytic solution; the parameters are artificial, and only for the purpose of illustrating our analytical results.
Example 1. Consider the system
where parameters are determined by k
1
= 2, k
-1
= 1, k
2
= 1.5, and K = 33. The substrate input function is determined by I(t) = 1 + 0.3 sin(2πt). Note that 0 <
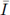 < 4.5. Numerical simulations are shown in the next figures, which exhibit an oscillatory behavior according to the Theorem 2.2.
< 4.5. Numerical simulations are shown in the next figures, which exhibit an oscillatory behavior according to the Theorem 2.2.
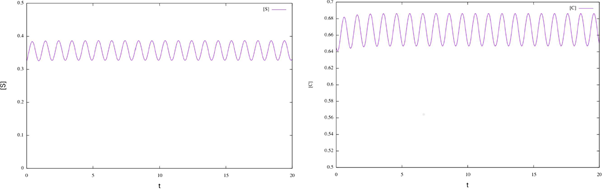
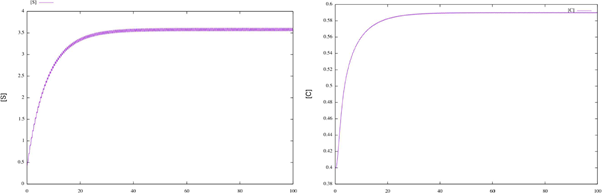
Figure 1 Time plots for enzymatic model (17). We can see that the solutions for the initial conditions S0 = 0.325 and C0 = 0.645 converge to the corresponding numerical approximation of the periodic orbit.
According to Theorem 2.2 the system has a periodic solution, which is globally attractive. To illustrate this fact, we consider different initial conditions for the system (17) and observe that the corresponding solutions tend the corresponding numerical approximation of the periodic orbit (see figure 2).
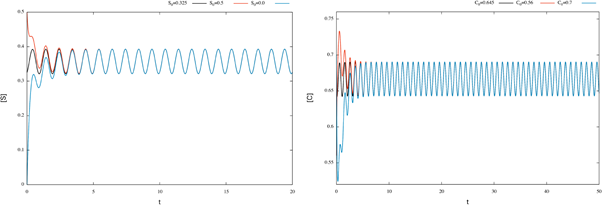
Figure 2 Time plots for enzymatic model (17), with different initial conditions. We can see that the corresponding numerical approximation of the periodic orbit behaves like a globally attractive orbit.
Example 2. Consider the system
where parameters are determined by β = 5, k 1 = 0.2, k -1 = 0.3, k 2 = 7, and K = 0.8. The substrate input function is determined by I(t) = cos 2 (2πt).