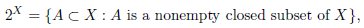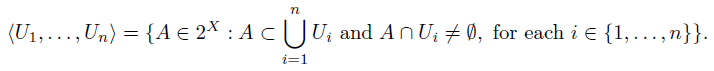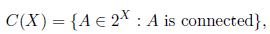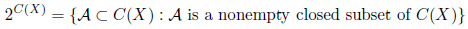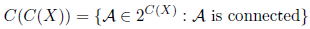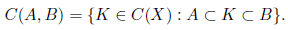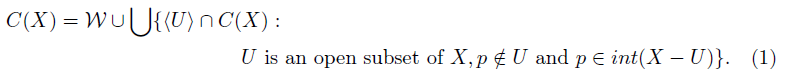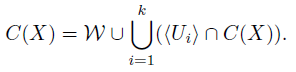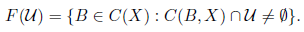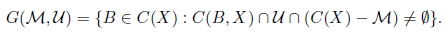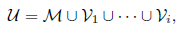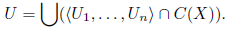1. Introduction
A continuum is a compact, connected Hausdorff space with more than one point. A metric continuum is a continuum with a metric d that generates its topology.
The property of Kelley for metric continua was introduced by J. L. Kelley as property 3.2 in [4, p. 26]; he used it to study the contractibility of hyperspaces (see [13, Chapter XVI] and [3, pp. 167-172]). In 1999, W. J. Charatonik [2, Definition 2.1] and W. Makuchowski [9, p. 124] extended the property of Kelley for continua; in particular, Charatonik shows an example of a homogeneous continuum that does not have the property of Kelley, and Makuchowski uses the property of Kelley to show that several definitions of local connectivity are equivalent in the hyperspace C(X) of a continuum X having the property of Kelley. Concerning the generalization of some properties of metric continua to continua, S. Macías studied the property of Kelley for continua and introduces the uniform Effros property [6, p. 60]. In [7] and [8], the author proved that several properties of Jones’ set function T , valid for metric continua, hold for continua as well.
In 1998, J. J. Charatonik and W. J. Charatonik defined the concepts of maximal limit continuum and strong maximal limit continuum, for metric continua [1, Definitions 3.2 and 3.3]; the authors used those definitions to show several properties of continua having the property of Kelley, and to show that some properties are equivalent to the property of Kelley. In this paper we extend the metric concepts of maximal limit continuum and strong maximal limit continuum, to continua, which we call Hausdorff maximal limit continuum and Hausdorff strong maximal limit continuum, respectively. We show that in metric continua, the definition of maximal limit continuum is equivalent to the definition of Hausdorff maximal limit continuum (Theorem 4.8), and the definition of strong maximal limit continuum is stronger that the definition of Hausdorff strong maximal limit continuum (Proposition 4.13). To end the paper, we show that the equivalences of [1, Theorem 3.11] still hold under these new extensions (Theorem 4.19).
2. Preliminaries
Given a continuum X, we consider the collection of all nonempty closed subsets of X, which is denoted by 2 X ; in other words,
topologized with the Vietoris topology, which can be described as follows: for each n ∈ N and each finite collection U 1 ,...,U n of open subsets of X, we define
The collection of all sets of the form hU 1 ,...,U n i, is a basis for a topology for 2 X , which is called the Vietoris topology [11, Definition 1.7]. The set 2 X , endowed with the Vietoris topology, is called hyperspace of closed subsets of X. Also, we consider the collection of all subcontinua of X, denoted and defined by
as a subspace of 2 X . The collection C(X) is called the hyperspace of subcontinua of X. It is known that if X is a continuum, then 2 X and C(X) are also continua [11, Theorems
4.9 and 4.10]. In this way, given a continuum X, we have that
and
are also continua.
If X is a topological space, given a subset A of X, the interior of A is denoted by int(A) and the closure of A by cl(A). Given A,B ∈ C(X) with A ⊂ B, we consider the collection
Remark 2.1. If A and B are subcontinua of X and A ⊂ B, then C(A,B) is a nonempty connected closed subset of C(X); in other words, C(A,B) is an element of C(C(X)).
Proof. Let L ∈ C(X)−C(A,B). We have that L−B ≠ ∅ or A−L ≠ ∅. If L−B ≠ ∅, then there exists x ∈ L−B. Consider an open subset U of X such that x ∈ U and U ∩B = ∅. Therefore, L ∈ hU,Xi and hU,Xi ∩ C(A,B) = ∅. Now, if A − L ≠ ∅, then there exists a ∈ A − L. Consider an open subset V of X such that a ∈ V and cl(V ) ∩ L = ∅. Notice that L ∈ hX −cl(V )i. Let L ′ ∈ hX −cl(V )i; then a /∈ L ′, consequently A * L ′. It follows that L ′ ∈/ C(A,B). Now, the proof that the hyperspace C(X) is arcwise connected, by McWaters [10, Theorem, p. 1209] contains a proof that sets of the form C(A,B) are connected.
Let X be a continuum and A ⊂ 2 X ; we denote SA = {x ∈ X: there exists A ∈ A such that x ∈ A}.
Now, if X is a metric continuum, the hyperspace 2 X is also considered with the Hausdorff metric, which we denote by H. It is known that the Hausdorff metric of 2 X generates the Vietoris topology [13, (0.13) Theorem]. Given r > 0, x ∈ X and A ∈ 2 X , let B(r,x) be the open ball in X with center x and radius r and let B H (r,A) be the open ball in 2 X with center A and radius r; also, let N d (r,A) = S{B(r,x) : x ∈ A}.
Given a function between spaces X and Y , f: X → Y , A ⊂ X, and B ⊂ Y , let f[A] = {f(a) : a ∈ A} the image of A under f, and f −1[B] = {x ∈ X: f(x) ∈ B}, the inverse image of B under f.
3. Limit superior of nets in 2 X
A directed set is a pair (D,≤), where D is a nonempty set and ≤ is a partial order in D, such that for each a,b ∈ D, there exists c ∈ D such that a ≤ c and b ≤ c. A net in X is a function f: D → X, where D is a directed set; we also denote a net f by {x d } d ∈ D , where x d = f(d), for each d ∈ D.
We recall that a net {x d } d ∈ D in X converges to a point x ∈ X, if for each open subset U of X with x ∈ U, there exists n ∈ D such that if m ∈ D and n ≤ m, then x m ∈ U.
Given a continuum X, if {A d } d ∈ D is a net in 2 X , we define the limit superior of {A d } d ∈ D as follows:
limsup{A d } d ∈ D = {x ∈ X: for each open subset U of X with x ∈ U and for each d ∈ D, there exists m ∈ D such that m ≥ d and U ∩ A m ≠ ∅}.
The limit superior of a net in 2 X was first considered by Mrówka [12, p. 237]. We present two properties of the limit superior that will be used in this paper.
Lemma 3.1 ([12, 4., p. 238]). Let X be a continuum and let {A d } d ∈ D be a net in 2 X . Then limsup{A d } d ∈ D is an element of 2 X .
Lemma 3.2. Let X be a continuum and let {A d } d ∈ D be a net in C(X) converging to A ∈ C(X). Then A ∈ limsup{C(A d ,X)} d ∈ D .
Proof. Let U be an open subset of C(X) such that A ∈ U. Since {A d } d ∈ D converges to A, there exists n ∈ D such that for each m ∈ D, if n ≤ m, then A m ∈ U. Let s ∈ D and choose m ∈ D such that s ≤ m and n ≤ m; then A m ∈ U and A m ∈ C(A m ,X), hence U ∩ C(A m ,X) ≠ ∅. We have proved that A ∈ limsup{C(A d ,X)} d ∈ D .
4. Main results
In 1942, J. L. Kelley introduced the concept of property of Kelley for metric continua, originally called property 3.2 [4, p. 26]:
Definition 4.1. Let X be a metric continuum with metric d. We say that X has the property of Kelley if for each ε > 0 there exists δ > 0 such that for any p,q ∈ X, if d(p,q) < δ, then for each K ∈ C({p},X), there exists L ∈ C({q},X) such that H(K,L) < ε.
Let us recall that H is the Hausdorff metric of the hyperspaces 2 X and C(X); for A ∈ 2 X and r > 0, B H (r,A) is the open ball in 2 X of radius r and center A.
In 1999, W. J. Charatonik [2, Definition 2.1] and W. Makuchowski [9, p. 124] introduced independently the concept of property of Kelley for continua, as follows:
Definition 4.2. Let X be a continuum and p ∈ X. We say that X has the property of Kelley at p, if for each K ∈ C({p},X) and for each open subset U of C(X) with K ∈ U, there exists an open subset U of X with p ∈ U such that if q ∈ U, then there exists L ∈ C({q},X) ∩ U. We say that X has the property of Kelley if it has the property of Kelley at each of its points.
In [14, p. 292] the author says that the property of Kelley and the pointwise version of property of Kelley are equivalent for metric continua. Since it is clear that the pointwise version of the property of Kelley on [14, p. 292] is equivalent to the pointwise version of the property of Kelley given in Definition 4.2, we have that Definition 4.2 is equivalent to Definition 4.1.
In the following theorem we summarize two characterizations of continua having the property of Kelley. The equivalence of (1) and (3) was proved by Wardle for metric continua in [14, (2.2) THEOREM], and Charatonik mentions without proof that the result is valid for continua [2, Proposition 2.3]; Makuchowski proved the equivalence of (1) and (2) [9, Theorem 11]. For the convenience of the reader, we prove (2) ⇒ (3) and (3) ⇒ (1) .
Theorem 4.3. Let X be a continuum. Then the following conditions are equivalent:
(1) X has the property of Kelley.
(2) For each open subset U of C(X), it holds that SU is an open subset of X.
(3) The function f: X → 2 C(X) , defined by f(p) = C({p},X) for each p ∈ X, is continuous.
Proof. In this proof, since we consider the hyperspaces 2 X and 2 C(X) , we will use the notation h·i2 C (X) to denote the basic open sets of the Vietoris topology in 2 C(X) .
We prove that (2)⇒(3). Let U be an open subset of 2 C(X) and let p ∈ f −1[U]. Notice that C({p},X) = f(p) ∈ U. Thus there are open subsets, U1 ,...,U n , of C(X) such that C({p},X) ∈ hU1 ,...,U n i2 C (X) ⊂ U. By (2), for each i ∈ {1,...,n} we have that SU i is an open subset of X. Since C({p},X) ∩ U i ≠ ∅, for each i ∈ {1,...,n}, there exists A ∈ C({p},X) ∩ U i ; since p ∈ A ∈ U i , we have that p ∈ SU i , for each i ∈ {1,...,n}.
Let W = U1 ∪···∪U n and define V ′ = {v ∈ X: C({v},X) ⊂ W}. We will show that V ′ is a neighborhood of p in X. In order to prove this assertion, first we prove that
Notice that C({p},X) ⊂ W. If A ∈ C(X) and A /∈ C({p},X), then we choose two disjoint nonempty open subsets U and V of X such that A ⊂ U and p ∈ V . Then A ∈ hUi ∩ C(X) and p ∈ V ⊂ int(X − U), and thus (1) follows.
On the other hand, by compactness of C(X), there exist k ∈ ℕ and U 1 ,...,U k open subsets of X such that p ∈ int(X − U i ) for each i ∈ {1,...,k} and
Notice that
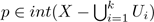 . Let
. Let
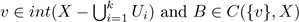 ; notice that if B ∈ hU
i
i, then v ∈ U
i
; therefore
; notice that if B ∈ hU
i
i, then v ∈ U
i
; therefore 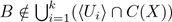 , and B ∈ W. We have proved that C({v},X) ⊂ W for each
, and B ∈ W. We have proved that C({v},X) ⊂ W for each
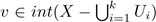 , then V
′ is a neighborhood of p.
, then V
′ is a neighborhood of p.
Now, let
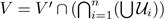 . We have that V is a neighborhood of p. We consider a point v ∈ V , and we will prove that f(v) ∈ hU1
,...,U
n
i2
C
(X)
. Notice that v ∈ V ⊂ V
′, therefore,
. We have that V is a neighborhood of p. We consider a point v ∈ V , and we will prove that f(v) ∈ hU1
,...,U
n
i2
C
(X)
. Notice that v ∈ V ⊂ V
′, therefore,
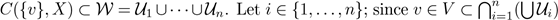 , then
, then
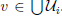 . Hence, there exists D ∈ U
i
such that v ∈ D ∈ U
i
. This implies that D ∈ C({v},X) ∩ U
i
≠ ∅. Thus, f(v) = C({v},X) ∈ (U1
,...,U
n
)2
C(X)
⊂ 𝔘, therefore f(v) ∈ 𝔘. We obtained that f
−1[𝔘] is an open subset of X, and this ends the implication (2)⇒(3).
. Hence, there exists D ∈ U
i
such that v ∈ D ∈ U
i
. This implies that D ∈ C({v},X) ∩ U
i
≠ ∅. Thus, f(v) = C({v},X) ∈ (U1
,...,U
n
)2
C(X)
⊂ 𝔘, therefore f(v) ∈ 𝔘. We obtained that f
−1[𝔘] is an open subset of X, and this ends the implication (2)⇒(3).
We see that (3)⇒(1). Let p ∈ X, let K ∈ C({p},X) and let U be an open subset of C(X) such that K ∈ U. Notice that C({p},X) ∈ (U,C(X))2 C(X) , because C({p},X) ⊂ U ∪ C(X) = C(X), C({p},X) ∩ U ≠ ∅ and C({p},X) ∩ C(X) = C({p},X) ≠ ∅. Let U = f −1[hU,C(X)i2 C (X) ]; we have that U is an open subset of X and p ∈ U. Let q ∈ U, then f(q) ∈ hU,C(X)i2 C (X) , hence f(q) = C({q},X) and C({q},X)∩U ≠ ∅. Let L ∈ C({q},X)∩ U, then q ∈ L and L ∈ U. Therefore, X has the property of Kelley.
In 1998, J. J. Charatonik and W. J. Charatonik introduced the following definition for metric continua [1, Definition 3.2.]:
Definition 4.4. Let K be a subcontinuum of a metric continuum X. A subcontinuum M ⊂ K is called a maximal limit continuum in K provided that there is a sequence {M n } n ∈N of subcontinua of X, converging to M, such that for each sequence {M n ′ } n ∈N of subcontinua of X with M n ⊂ M n ′ for each n ∈ N, if {M n ′ } n ∈N converges to some M ′ ∈ C(K), then M ′ = M.
For U ⊂ C(X), we define the collection
We extend the concept maximal limit continuum for continua as follows:
Definition 4.5. Let K be a subcontinuum of a continuum X. A subcontinuum M ⊂ K is called Hausdorff maximal limit continuum in K provided that for each subcontinuum L ⊂ X with M ( L ⊂ K there is an open subset U of C(X) such that L ∈ U and the collection F(U) is not neighborhood of M.
Remark 4.6. Let K be a subcontinuum of a continuum X. If M ⊂ K is a Hausdorff maximal limit continuum in K, then for each subcontinuum L ⊂ X with M ( L ⊂ K there exists an open subset U of C(X) such that L ∈ U, and for each neighborhood V ⊂ C(X) of M there exists B ∈ V such that C(B,X) ∩ U = ∅.
Proof. Let L be a subcontinuum of X such that
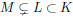 . By hypothesis, there is an open subset U of C(X) such that L ∈ U and the collection F(U) is not a neighborhood of M. Now, let V ⊂ C(X) be a neighborhood of M. Since F(U) is not neighborhood of M, we obtain that
. By hypothesis, there is an open subset U of C(X) such that L ∈ U and the collection F(U) is not a neighborhood of M. Now, let V ⊂ C(X) be a neighborhood of M. Since F(U) is not neighborhood of M, we obtain that
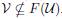 . Hence, there exists B ∈ V such that C(B,X)∩U = ∅.
. Hence, there exists B ∈ V such that C(B,X)∩U = ∅.
The following lemma follows from the definition.
Lemma 4.7. Let K be a subcontinuum of a continuum X. Then K is a Hausdorff maximal limit continuum in K.
We are going to prove that in metric continua Definitions 4.4 and 4.5 are equivalent:
Theorem 4.8. Let X be a metric continuum, K ∈ C(X) and M ∈ C(K). Then the following statements are equivalent:
(1) M is a maximal limit continuum in K.
M is a Hausdorff maximal limit continuum in K.
Proof. We prove that (1)⇒(2). Assume that X is a metric continuum that satisfies (1) but does not satisfy (2). Let {M
n
}
n
∈N be the sequence converging to M, given by (1). Since X does not satisfy (2), there exists L ∈ C(X) such that M ( L ⊂ K and for each k ∈ ℕ, we have that the set
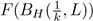 is a neighborhood of M. Since {M
n
}
n
∈ℕ converges to M, for each k ∈ ℕ there exists n
k
∈ N such that for every n ≥ n
k
, we have that
is a neighborhood of M. Since {M
n
}
n
∈ℕ converges to M, for each k ∈ ℕ there exists n
k
∈ N such that for every n ≥ n
k
, we have that
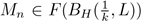 . We can assume that the sequence {n
k
}
k
∈N is strictly increasing. Let n ∈ N with n ≥ n
1, let k ∈ N such that n
k
≤ n < n
k+1
; thus we obtain that
. We can assume that the sequence {n
k
}
k
∈N is strictly increasing. Let n ∈ N with n ≥ n
1, let k ∈ N such that n
k
≤ n < n
k+1
; thus we obtain that
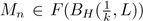 , therefore
, therefore
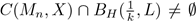 ; choose M
n
′ ∈ C(M
n
,X) ∩ B
H
(
k
1
,L). Then the sequence
; choose M
n
′ ∈ C(M
n
,X) ∩ B
H
(
k
1
,L). Then the sequence
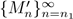 converges to L ⊂ K and L ≠ M, which is a contradiction.
converges to L ⊂ K and L ≠ M, which is a contradiction.
We prove that (2)⇒(1). For each L ∈ C(M,K) − {M}, let U
L
be an open subset of C(X) such that L ∈ U
L
and F(U
L
) is not neighborhood of M. Since C(M,K) is a compact metric space, let {U
i
: i ∈ ℕ} be a countable subcover of the cover {U
L
: L ∈ C(M,K) − {M}} of the space C(M,K) − {M}. We can choose a sequence {M
n
}
n
∈N in C(X) such that H(M,M
n
) ≤ 1 n , for each n ∈ ℕ, and satisfying the following properties: M1 ∉ F(U1), M2 ∉ F(U2), M3 ∉ F(U1), M4 ∉ F(U2), M5 ∉F(U3), M6 ∉ F(U1), M7 ∉ F(U2), M8 ∉F(U3), M9 ∉ F(U4), and so on inductively. We consider a sequence {M
n
′ }
n
∈ℕ in C(X) convergent to some M′ ∈ C(K) and such that M
n
⊂ M
n
′ , for each n ∈ N; hence, M ⊂ M′. Assume that M ≠ M ′, then there exists k ∈ N such that M′ ∈ U
k
, and choose a subsequence
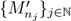 of the sequence {M
n
′ }
n
∈ℕ such that M
nj
∈/ F(U
k
), for each j ∈ ℕ. So, for each j ∈ ℕ, we have that C(M
nj
,X) ∩ U
k
= ∅, then
of the sequence {M
n
′ }
n
∈ℕ such that M
nj
∈/ F(U
k
), for each j ∈ ℕ. So, for each j ∈ ℕ, we have that C(M
nj
,X) ∩ U
k
= ∅, then
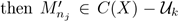 . Since C(X) − U
k
is a closed subset of C(X), we have that M′ ∈ C(X) − U
k
, which is a contradiction. We conclude that M = M′ ‘.
. Since C(X) − U
k
is a closed subset of C(X), we have that M′ ∈ C(X) − U
k
, which is a contradiction. We conclude that M = M′ ‘.
In 1998, J. J. Charatonik and W. J. Charatonik introduced the following definition for metric continua [1, Definition 3.3.]:
Definition 4.9. Let K be a subcontinuum of a metric continuum X. A continuum M ⊂ K is called a strong maximal limit continuum in K provided that there is a sequence {M n } n ∈N of subcontinua of X converging to M, such that for each subsequence {M nk } k ∈N of {M n } n ∈ℕ and for each sequence {M k ′} k ∈N of subcontinua of X with M nk ⊂ M k ′ for each k ∈ ℕ, if {M k ′} k ∈ℕ converges to some M′’ ∈ C(K), then M′´’ = M.
For M,U ⊂ C(X), we define the collection
Concerning the definition of strong maximal limit continuum, we propose the following concept:
Definition 4.10. Let K be a subcontinuum of a continuum X. A subcontinuum M ⊂ K is called Hausdorff strong maximal limit continuum in K provided that for each open subset M of C(X) such that M ∈ M, there exists an open subset U of C(X) such that C(M,K) ⊂ U and the collection G(M,U) is not neighborhood of M.
Remark 4.11. Let K be a subcontinuum of a continuum X. If M ⊂ K is a Hausdorff strong maximal limit continuum in K, then for each open subset M of C(X) such that M ∈ M, there exists an open subset U of C(X) such that C(M,K) ⊂ U, and for each neighborhood V of M in C(X) there exists B ∈ V such that C(B,X)∩U∩(C(X)−M) = ∅, equivalently C(B,X) ∩ U ⊂ M.
Proof. Let M be an open subset of C(X) such that M ∈ M. By hypothesis, there is an open subset U of C(X) such that C(M,K) ⊂ U and the collection G(M,U) is not a neighborhood of M. Let V be a neighborhood of M in C(X). Since G(M,U) is not a neighborhood of M, we obtain that V * G(M,U). Hence, there exists B ∈ V such that C(B,X) ∩ U ⊂ M.
Lemma 4.12. Let K be a subcontinuum of a continuum X. Then K is a Hausdorff strong maximal limit continuum in K.
Proof. Let M be an open subset of C(X) such that K ∈ M. Since C(K,K) = {K} ⊂ M, we consider U = M. Notice that G(M,U) = {B ∈ C(X) : C(B,X)∩U ∩(C(X)−M) ≠ ∅} = ∅, which is not a neighborhood of K.
We show that a strong maximal limit continuum is also a Hausdorff strong maximal limit continuum.
Proposition 4.13. Let X be a metric continuum, K ∈ C(X) and M ∈ C(K). If M is a strong maximal limit continuum in K, then M is a Hausdorff strong maximal limit continuum in K.
Proof. Let d be a metric on X, and let H be the Hausdorff metric on C(X). Let {M n } n ∈N be a sequence that witnesses that M is a strong maximal limit continuum in K. We consider an open subset M of C(X) such that M ∈ M. Suppose that for each open subset U of C(X) such that C(M,K) ⊂ U, we have that the collection G(M,U) is a neighborhood of M. Now, for each . k ∈ ℕ, let Uk = NH( 1 𝑘 , C(M,K)) Notice that C(M,K) ⊂ U k , then the collection G(M,U k ) is a neighborhood of M. Inductively we can define a subsequence {M nk } k ∈ℕsuch that M nk ∈ G(M,U k ), for each k ∈ N, hence C(M nk ,X) ∩ U k ∩ (C(X) − M) ≠ ∅. Consider an element M k ′ ∈ C(M nk ,X) ∩ U k ∩ (C(X) − M), for each k ∈ N. Taking a subsequence if necessary, we may assume that {M k ′} k ∈N converges to an element M′ ∈ C(X). For each k ∈ N, notice that M k ′ ∈ U k and M k ′ ∈ C(X)−M, then M′ ∈ C(M,K) and M′ ∈ C(X)−M, therefore M’′ ≠ M, which contradicts the choice of the sequence {M n } n ∈N.
Question 4.14. Let X be a metric continuum, K ∈ C(X) and M ∈ C(K), such that M is a Hausdorff strong maximal limit continuum in K. Is it true that M is a strong maximal limit continuum in K?
Proposition 4.15. Let X be a continuum, let K be a subcontinuum of X, let {A d } d ∈ D be a net in C(X) converging to A ∈ C(K) and let M be a maximal element in C(K)∩limsup{C(A d ,X)} d ∈ D (with respect to inclusion). Then M is a Hausdorff strong maximal limit continuum in K.
Proof. Assume that M is not a Hausdorff strong maximal limit continuum in K. Then there exists an open subset M of C(X) with M ∈ M such that for each open subset U of C(X) with C(M,K) ⊂ U, the collection G(M,U) is a neighborhood of M. For each L ∈ C(M,K) − M we have that M ( L, and by maximality of M, we obtain that L /∈ limsup{C(A d ,X)} d ∈ D . Thus there exists an open subset V L of C(X) such that L ∈ V L , and exists d L ∈ D such that if m ≥ d L , then V L ∩ C(A m ,X) = ∅. By compactness of C(M,K) − M we obtain a finite subcover, {V1,V2,...,V i }, for some i ∈ N, of {V L : L ∈ C(M,K) − M} which covers C(M,K) − M, and for each V j , there exists an element d j ∈ D such that if m ≥ d j , then V dj ∩ C(A m ,X) = ∅. We consider
which is an open subset of C(X) and C(M,K) ⊂ U. Therefore, G(M,U) is a neighborhood of M. Since M ∈ limsup{C(A d ,X)} d ∈ D , for each d ∈ D there exists m ∈ D such that m ≥ d and G(M,U) ∩ C(A m ,X) ≠ ∅. Choose n ∈ D such that n ≥ d j , for each j ∈ {1,2,...,i}, and m ≥ n such that G(M,U) ∩ C(A m ,X) ≠ ∅. Consider B ∈ G(M,U) ∩ C(A m ,X). Notice that A m ⊂ B and C(B,X) ∩ U ∩ (C(X) − M) ≠ ∅. Since C(B,X) ⊂ C(A m ,X), then C(A m ,X) ∩ U ∩ (C(X) − M) ≠ ∅. Notice that C(A m ,X)∩V j = ∅, for each j ∈ {1,2,...,i}, thus C(A m ,X)∩U = C(A m ,X)∩M, and ∅ ≠ C(A m ,X)∩ U ∩ (C(X) − M) = C(A m ,X) ∩ M ∩ (C(X) − M) = ∅, which is a contradiction. This ends the proof that M is a Hausdorff strong maximal limit continuum in K.
We will prove that Theorem 3.11 of [1] is still valid under these new definitions. We start with two lemmas.
Lemma 4.16. Let X be a continuum with the property of Kelley, K ∈ C(X) and M ∈ C(K). If M ≠ K, then M is not a Hausdorff maximal limit continuum in K.
Proof. Suppose that a continuum X has the property of Kelley, K ∈ C(X) and M ∈ C(K) such that M is a Hausdorff maximal limit continuum in K and M ≠ K. For L = K, by Remark 4.6 there exists an open subset U of C(X) with L ∈ U such that for each neighborhood V of M in C(X) there exists B ∈ V such that C(B,X) ∩ U = ∅. Consider U1,...,U n open subsets of X such that L ∈ hU1,...,U n i ∩ C(X) ⊂ U. Let
By Theorem 4.3, we have that U is an open subset of X; consequently L ∈ hUi ∩ C(X), since M ⊂ L; then M ⊂ U. Let V = hUi ∩ C(X); then there exists B ∈ V such that C(B,X) ∩ U = ∅. Let D ∈ V, choose a point d ∈ D ⊂ U, then there exists J ∈ hU1,...,U n i∩C(X) such that d ∈ J. Since D∪J ⊂ U1∪···∪U n and (D∪J)∩U i ≠ ∅, for each i ∈ {1,...,n}. It follows that D ∪ J ∈ hU1,...,U n i ∩ C(X) ⊂ U. Notice that D ∪ J ∈ C(D,X). Therefore, C(D,X) ∩ U ≠ ∅, which is a contradiction.
Lemma 4.17. Let K be a subcontinuum of a continuum X and let M be a subcontinuum of K. If M is a Hausdorff strong maximal limit continuum in K, then M is a Hausdorff maximal limit continuum in K.
Proof. Let L ∈ C(M,K) with L ≠ M. Consider disjoint nonempty open subsets M1 and M2 of C(X) such that M ∈ M1 and L ∈ M2. By hypothesis, there exists an open subset U′ of C(X) such that C(M,K) ⊂ U′ and the set G(M1,U′) is not a neighborhood of M.
Let U = U′ ∩ M2. We will show that the set F(U) is not a neighborhood of M, first we prove that:
Indeed, let B ∈ F(U); then B ∈ C(X) and C(B,X)∩U ≠ ∅, equivalently C(B,X)∩U′ ∩ M2 ≠ ∅, hence C(B,X)∩U′ ∩(C(X)−M1) ≠ ∅. We have proved that B ∈ G(M1,U′). Thus (2) follows. Since G(M1,U′) is not a neighborhood of M, then F(U) is not a neighborhood of M.
Corollary 4.18. Let X be a continuum with the property of Kelley, K ∈ C(X) and M ∈ C(K). If M ≠ K, then M is not a Hausdorff strong maximal limit continuum in K.
To conclude this paper, we prove that Theorem 3.11 of [1] is still valid under these new definitions.
Theorem 4.19. Let X be a continuum; then, the following statements are equivalent:
(1) X has the property of Kelley.
(2) For each subcontinuum K of X, the only Hausdorff maximal limit continuum in K is K itself.
(3) For each subcontinuum K of X, the only Hausdorff strong maximal limit continuum in K is K itself.
Proof. By Lemma 4.7 and Lemma 4.16, we have that (1)⇒(2).
By Lemma 4.12 and Lemma 4.17, we have that (2)⇒(3).
We prove (3)⇒(1). Consider U an open subset of C(X). By Theorem 4.3, it is sufficient to show that SU is an open subset of X. Asumme that SU is not open, and choose a point p ∈ SU − int(SU). Let
be a directed set, where V1 ≤ V2 if V2 ⊂ V1, for each V1,V2 ∈ D. For each V ∈ D, choose
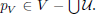 Notice that the net {p
V
}
V
∈D converges p in X and p
V
∈/ SU, for each V ∈ D. Let K ∈ U such that p ∈ K. Since the net {{p
V
}}
V
∈D converges to {p} in C(X), by Lemma 3.2 we have that {p} ∈ limsup{C({p
V
},X)}
V
∈D. Therefore C(K)∩ limsup{C({p
V
},X)}
V
∈D ≠ ∅. By the Kuratowski-Zorn Lemma [5, p. 33], there exists M ∈ C(K) ∩ limsup{C({p
V
},X)}
V
∈D maximal with respect to inclusion. By Proposition 4.15, we have that M is a Hausdorff strong maximal limit continuum in K. By (3), we have that M = K. It follows that K ∈ limsup{C({p
V
},X)}
V
∈D; since U is an open subset of C(X) and K ∈ U, then for each R ∈ D, there exists S ∈ D such that S ≥ R and U ∩ C({p
S
},X) ≠ ∅. Choose B ∈ U ∩ C({p
S
},X), then p
S
∈ B ∈ U. Hence p
S
∈ SU, which is a contradiction. We have proved that SU is an open subset of X. This ends the proof of the theorem.
Notice that the net {p
V
}
V
∈D converges p in X and p
V
∈/ SU, for each V ∈ D. Let K ∈ U such that p ∈ K. Since the net {{p
V
}}
V
∈D converges to {p} in C(X), by Lemma 3.2 we have that {p} ∈ limsup{C({p
V
},X)}
V
∈D. Therefore C(K)∩ limsup{C({p
V
},X)}
V
∈D ≠ ∅. By the Kuratowski-Zorn Lemma [5, p. 33], there exists M ∈ C(K) ∩ limsup{C({p
V
},X)}
V
∈D maximal with respect to inclusion. By Proposition 4.15, we have that M is a Hausdorff strong maximal limit continuum in K. By (3), we have that M = K. It follows that K ∈ limsup{C({p
V
},X)}
V
∈D; since U is an open subset of C(X) and K ∈ U, then for each R ∈ D, there exists S ∈ D such that S ≥ R and U ∩ C({p
S
},X) ≠ ∅. Choose B ∈ U ∩ C({p
S
},X), then p
S
∈ B ∈ U. Hence p
S
∈ SU, which is a contradiction. We have proved that SU is an open subset of X. This ends the proof of the theorem.