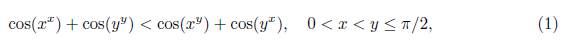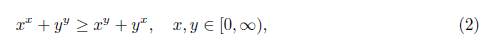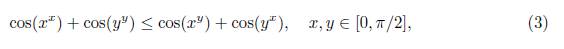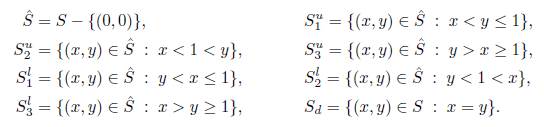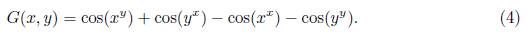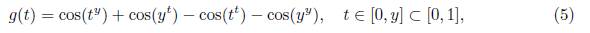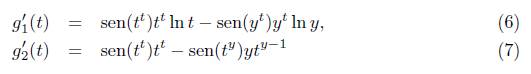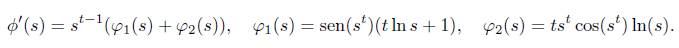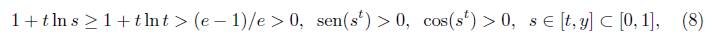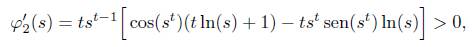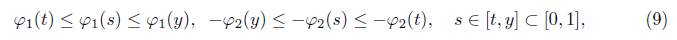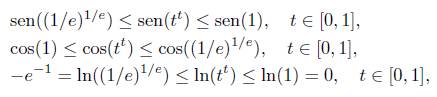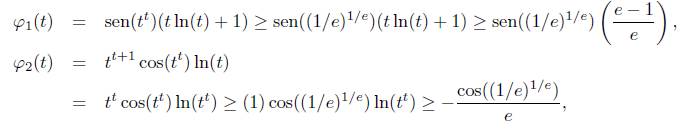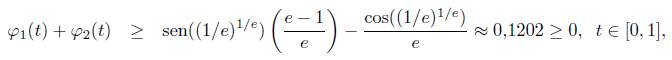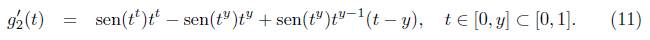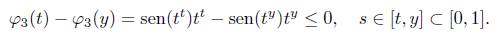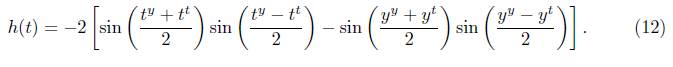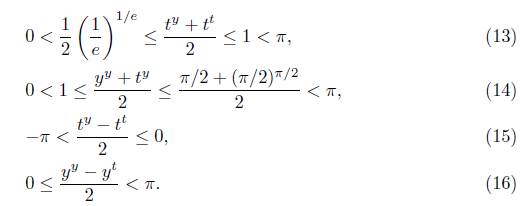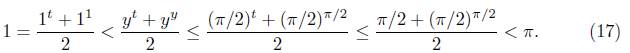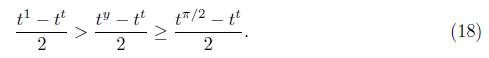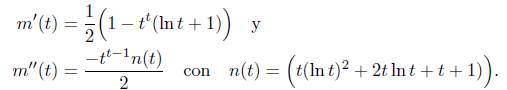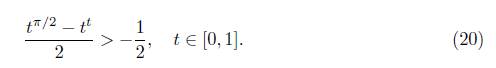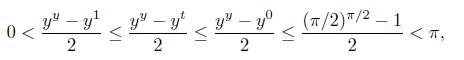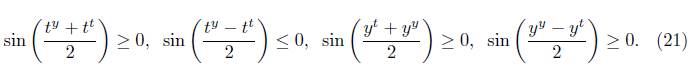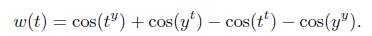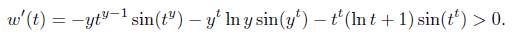Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Citado por Google 
Similares en
SciELO 
Similares en Google 
Permalink
1. Introducción
La siguiente desigualdad
fue conjeturada por Özban en [15] y fue probada recientemente por Matejíčka [11]. Se recuerda que la introducción de varias desigualdades algebraico-trigonométricas por Özban [15], se inspiró en la siguiente desigualdad exponencial-potencial
que fue probada de forma independiente por Laub-Ilani [6, 5] y Zeikii-Cîrtoaje-Berndt [17, 2]. Para obtener detalles importantes sobre generalizaciones, extensiones y desigualdades relacionadas con (2), consultar las referencias [4, 3, 1, 7, 8, 9, 10, 12, 13, 14, 16]. Además, se observa que la prueba de (1) desarrollada por Matejícka en [11] se basa en métodos de análisis matemático y numérico. Sin embargo, se puede construir una prueba alternativa basada en las propiedades elementales de las funciones exponencial, potencial y trigonométricas. Así, el objetivo de este artículo es presentar una prueba alternativa de (1) y extender la desigualdad al caso x,y ∈ [0, π/2], es decir, se demostrará el siguiente teorema:
Teorema 1.1. La siguiente desigualdad
es válida.
2. Prueba del Teorema 1.1
Se introduce la notación S = [0, π/2] × [0, π/2] y los siguientes conjuntos
Se observa que la familia de conjuntos {S d , S u 1 , S u 2 , S u 3 , S l 1 , S l 2 , S l 3} es una partición de S.
Además, se considera la función G: S → ℝ definida por
Entonces, para probar la desigualdad (3), demostraremos G(x,y) ≥ 0 en cada conjunto de la partición.
Caso (x, y) Є S d . La desigualdad (3) se satisface en S d , dado que (3) en S d es equivalente a la identidad: cos(xx) + cos(xx) = cos(xx) + cos(xx).
Caso (x,y) Є S u 1 . En este caso se sigue un procedimiento análogo a la demostración del Teorema 2.3 en [15]. Seleccionamos arbitrariamente y Є (0,1] y se define la función g: [0, y] → ℝ mediante la relación g(t) = G(t,y) siendo G la función dada en (4). Note que x < y ≤ 1 implica que 0 ≤ t ≤ y ≤ 1, es decir [0, y] ⊂ [0,1]. Así la función g es definida explicitamente por
la cual se estudiará en lo que sigue. Más precisamente, se demostrará que la función g, es decreciente sobre su intervalo de definición [0,y]. Para ello se observa que la derivada de g se puede escribir como g'(t) = g’ 1 (t) + g’2 (t) con las funciones g' 1 y g’2 dadas por las reglas de correspondencia
y se analiza el signo de cada una de estas funciones sobre [0, y], demostrando que ambas son negativas sobre [0, y].
Para estudiar el signo de g’ 1 nos apoyamos en la función ϕ (s) = s t sen(st) ln s definida para s Є [t, y], cuya derivada sobre [t, y] es expresada de la siguiente manera
Observando que las siguientes desigualdades se cumplen
deducimos que φ’1(s) = ts t-1 cos(st)(t ln s + 1) + s -1 t sen(st) > 0 y en consecuencia la función φ1 es creciente sobre [t, y]. En el caso de la función p 2 se tiene
debido a que el primer término es positivo por la primera desigualdad dada en (8) y el segundo término por el hecho que ln(s) ≤ 0 para s ≤ 1. Así, tenemos que la función φ2 es creciente sobre [t, y]. Equivalentemente, se tiene que la función - φ2 es decreciente sobre [t, y].
El crecimiento de φ1 y el decrecimiento de - φ2 implican que las siguientes desigualdades
sean válidas para t ≤ s ≤ y. Además, es posible demostrar que φ1 ( t) > - φ2 ( t) para t Є [0,1]. Observemos que para t Є [0,1] el recorrido de la función t t es [(1/e)1/e, 1], es decir t t Є [(1/e)1/e, 1], lo cual conduce a la validez de las siguientes desigualdades
por aplicación directa de las propiedades de crecimiento o decrecimiento de las funciones seno, coseno y logaritmo natural sobre el intervalo [1/e, 1] ⊂ [0,1] ⊂ [0,7r/2]. Luego, es posible deducir las siguientes cotas inferiores
para t Є [0,1]. Así, tenemos que
es decir,
Luego, de (9) y (10) deducimos la cadena de desigualdades φ1(s) ≥ φ1 (t) > 0 ≥ - φ2 (t) ≥ - φ2 (s), lo cual demuestra que φ2(s) + φ2 (s) > 0 para s Є [t, y] ⊆ [0,1]. En consecuencia Ф'(s) > 0 sobre [t, y], implicando que Ф es creciente sobre [t, y]. De esta manera t ≤ s ≤ y implica Ф (t) ≤ Ф (s) ≤ Ф (y) o equivalentemente tenemos que la función g’1(t) = Ф (t) - Ф(y) es negativa sobre [0, y].
Para analizar el signo de la función g2, se observa que g’2 se puede reescribir como
Para s Є [t,y] ⊂ [0,1] definimos la función φ3(s) = sen(ts)ts. Observamos que la derivada de φ3 es tal que φ’3(s) = st s-1 (t s cos(ts) + sen(ts)) > 0 y así φ3 es creciente sobre [t, y]. Luego, t ≤ s ≤ y implica que φ3(t) ≤ φ3(s) ≤ φ3(y), es decir,
Ahora, utilizando esta última desigualdad y el hecho que sen(ty )yt y-1 (t - y) para t ≤ y, por la relación (11) deducimos que la función g’ 2 (t) es negativa sobre [0, y].
Habiendo demostrado que tanto g’1(t) como g’2(t) son negativas sobre [0, y], deducimos g'(t) = g’1(t) + g’2(t) ≤ 0 y claramente g(t) es decreciente sobre [0,y]. Ahora, el decrecimiento de g y el hecho que g(y) = 0 implican que g(0) ≥ g(t) ≥ g(y) = 0 para 0 ≤ t ≤ y. Demostrando así que la desigualdad g(t) = G(t,y) ≥ 0 se satisface para cada t Є [0, y], es decir, G(x, y) ≥ 0 sobre Su 1.
Caso (x,y) Є S u 2 . Fijando y Є (1,7π/2], se define la función h: [0,1] → ℝ mediante la relación h(t) = G(t,y) con G dado en (4). Aplicando las identidades trigonométricas de suma-producto se tiene
Se observa que
Las estimaciones en (13) son consecuencia de los siguientes hechos: la función definida de [0,1] a R por t → t y es creciente, y la función definida de [0,1] a ℝ por t → t* tiene un mínimo global en t = 1/e. En efecto, de cada uno de estos comportamientos se deduce que 0 ≤ t < 1 implica 0y - t y ≤ 1 y y que (1/e)1/e ≤ t t ≤ 1, respectivamente. En consecuencia de las desigualdades 0 ≤ t y < 1 y (1/e)1/e ≤ t* ≤ 1 se deduce (13). Ahora, (14) se deduce del hecho que la función definida de [1,n/2] a ℝ por y → (y t + y y )/2 es creciente y así la restricción para y dada por 1 < y - π/2 implica
En la penúltima desigualdad de (17) se utilizó el hecho que t → ( π/2)t es creciente y t Є [0,1]. Para demostrar (15) se observa que la función definida de [1,π/2] a ℝ por y → ( t y - t t ) /2 es decreciente y por lo tanto del hecho que 1 < y ≤ π/2 se deduce
Ahora, hay que obtener una cota superior para (t →t t )/2 y una cota inferior para (tπ/2 - t t )/2 y para ello utilizamos la función m: [0,1] → ℝ definida por m(t) = (t -t t )/2. La primera y segunda derivadas de la función m son dadas por
Se tiene que m’’ (t) < 0 sobre [0, 1] debido a la positividad de n la cual se deduce como sigue: n(t) → 1 cuando t → 0+, n(1) = 2, n(1/e) = 1, n(1/e3) = (16 + e3)/e3, n tiene un máximo en t = 1/e3 y un mínimo en t = 1/e3 lo cual implica que n(t) Є [1, 2] para cada t G [0,1]. Luego, m'(t) es decreciente sobre [0,1] y así m'(t) ≥ m'(1) = 0, es decir m es creciente sobre [0, 1]. En consecuencia la cota superior para m sobre [0, 1] es m(1) = 0 o equivalentemente
Ahora de la desigualdad t π/2 + 1 > 1 > t t , la cual se cumple para t Є [0,1], se deduce que
Luego, de (18), (19) y (20), obtenemos (15). Las estimaciones en (16) son consecuencia de que la función definida de [0,1] a ℝ por t → (y y - y t )/2 es decreciente, y así se tiene que (yy - y0)/2 > (y y - y t )/2 > (y y - y 1 )/2 sobre [0,1]. Ahora para y Є (0, π/2] se tiene que y y ≤ (π/2) π/2 lo cual implica la desigualdad (yy -y 0 )/2 ≤ ((π/2)π/2 -1)/2 < π y además dado que y es la tangente en y = 1 de la función estrictamente convexa y y se deduce que y y > y y en consecuencia (yy - y 1 )/2 > 0. Luego, resumiendo las desigualdades obtenidas se tiene la siguiente cadena
de donde claramente se deduce (16).
Ahora, mediante la aplicación de las propiedades de la función seno sobre [-π, π ], se tiene que las desigualdades en (13)-(16) implican
Al utilizar los signos de (21) en (12) se deduce que h(t) ≥ 0 para todo t Є [0,1] y cada y Є (0, π/2], concluyendo la prueba de la desigualdad (3) para (x, y) Є S u 2 .
Caso (x, y) Є S u 3 . En este caso se fija arbitrariamente y Є (1, π/2] y se define la función ω: (1, y] → ℝ mediante la relación ω(t) = G(t, y) con G definida en (4), es decir
Se observa que ω es decreciente sobre ]1,y] dado que t y ,y t ,t t Є [0, (π/2)n/2] ⊂ [0,π) implican
Luego ω (t) ≥ ω (y) = 0 para todo t Є (1, y] y similarmente a los casos anteriores se concluye que la desigualdad (3) es satisfecha sobre S u 3.
Caso (x,y) Є S u 1 U S u 2 U S u 3 . Para probar la desigualdad (3) sobre S l i para i = 1, 2, 3, se observa que (x, y) Є S l i si, y solo si, (y, x) Є S u i, entonces intercambiando (x, y) por (y, x) en la prueba para (x, y) Є S u se concluye que la desigualdad (3) es tambien válida sobre S¡.
