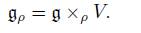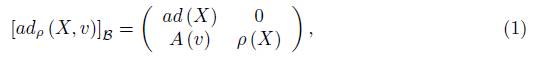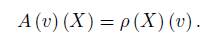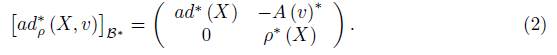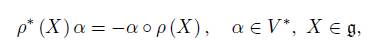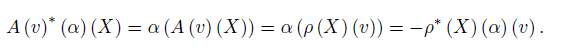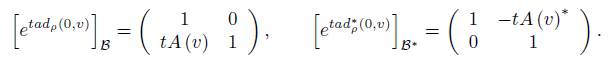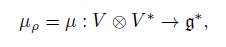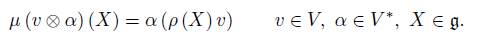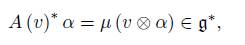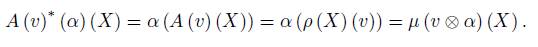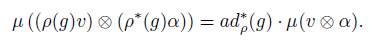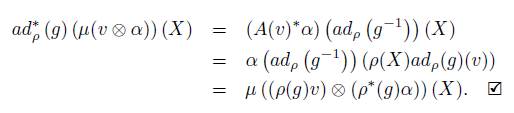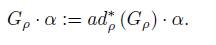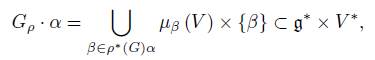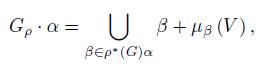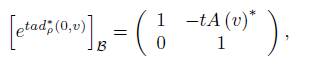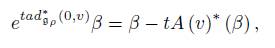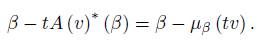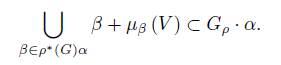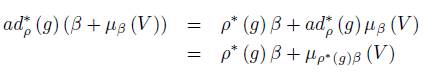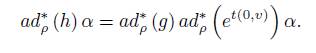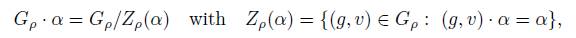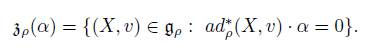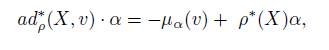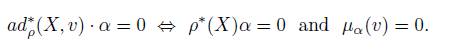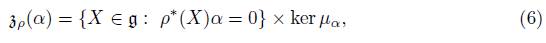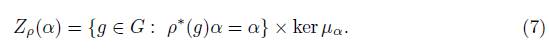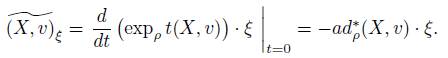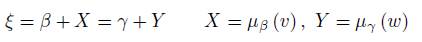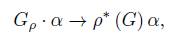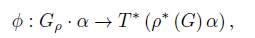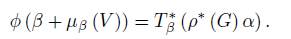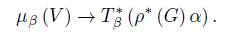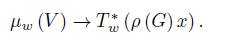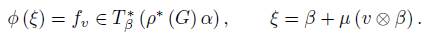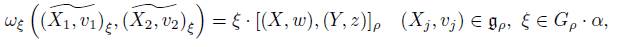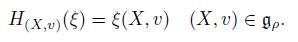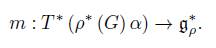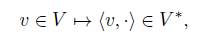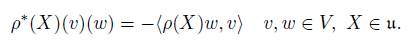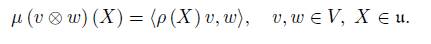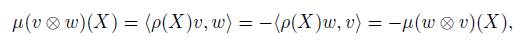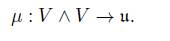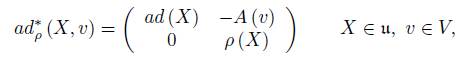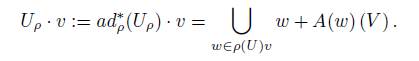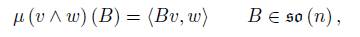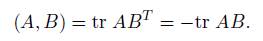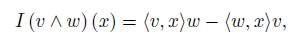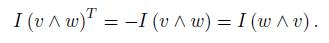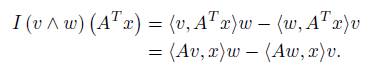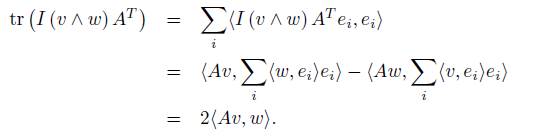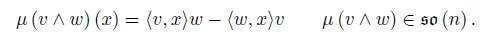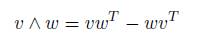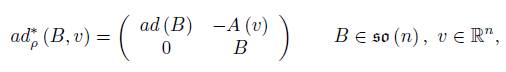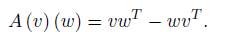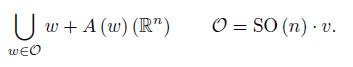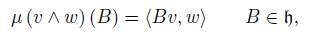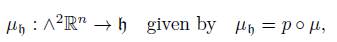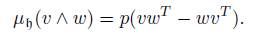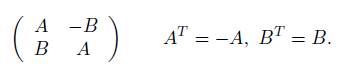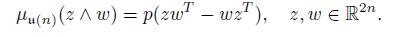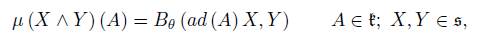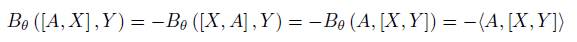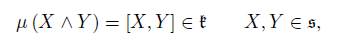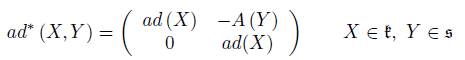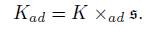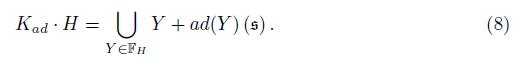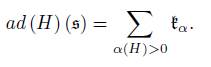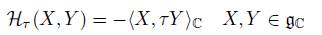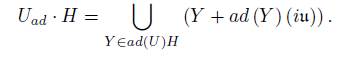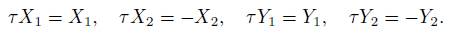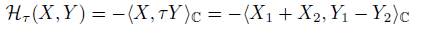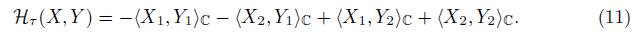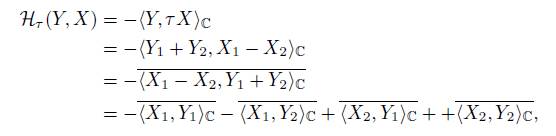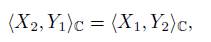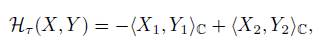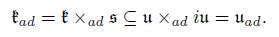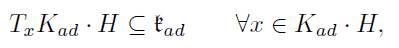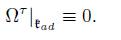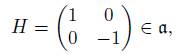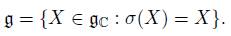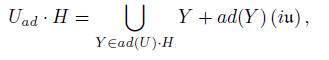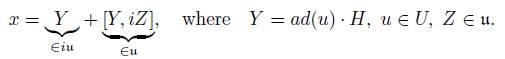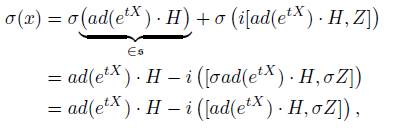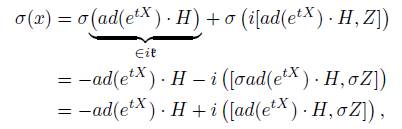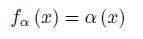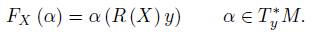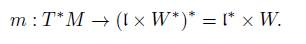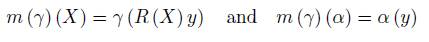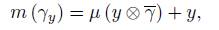English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1. Introduction
The symplectic structures and Lagrangian submanifolds of coadjoint orbits were stud-ied and developed by renowned mathematicians such as Kirillov, Arnold, Kostant, and Souriau from the early to the mid-1960s, although they had its roots in the work of Lie, Borel, and Weyl. Alternatively, there are several theories and applications to physics using general reduction theory, as in [2], [9], [10], and [11], among others. We study some applications of the semisimple Lie theory to symplectic geometry, in particular to find Lagrangian submanifolds on adjoint orbits. In this paper, we follow the next construction: let g be a non-compact semisimple Lie algebra with Cartan decomposition g = k ⊕s and Iwasawa decomposition g = ŧ ⊕ a ⊕ n with a ⊂ s maximal Abelian. In the under-lying vector space g, there is another Lie algebra structure ŧ ad = ŧ × ad s given by the semi-direct product defined by the adjoint representation of ŧ in s, which is viewed as an Abelian Lie algebra. Let G = Aut0g be the adjoint group of g (identity component of the automorphism group) and put K = exp ŧ ⊂ G. The semi-direct product K ad = K × ad s obtained by the adjoint representation of K in s has Lie algebra ŧ ad = ŧ × ad s, that orbit was studied in [1]. Then, we consider coadjoint orbits for both Lie algebras g and ŧ ad . These orbits are submanifolds of g ∗ that we identify with g via the Cartan-Killing form of g, so that the orbits are seen as submanifolds of g. These are just the adjoint orbits for the Lie algebra g while for ŧ ad they are the orbits in g of the representation of K ad obtained by transposing its coadjoint representation. The orbits through H ∈ g are denoted by ad (G) · H and K ad · H, respectively.
In Section 2, our goal is to generalize that construction, to get a wider variety of La-grangian submanifolds of any adjoint semisimple orbit. For this, we are going to change the usual structure of semisimple Lie algebras, i.e., with a new Lie bracket given by a convenient semi-direct product. This construction was inspired by [8], where the author defines a semi-direct product using a closed subgroup of a semi-simple Lie group and the vector space g (seeing g = Lie(G) as a vector space), but focused on solving some applications of control theory. In this way, the first part of this chapter is focused on the general construction of coadjoint orbits of this semi-direct structure. After that, we adapt those general results to the mentioned semi-direct product given by a Cartan decomposition.
In Section 3, we build some families of Lagrangian submanifolds on ad(G) · H with respect to the Hermitian symplectic form Ω τ , characterized by Cartan involutions on g. The idea and future goal of this result is: Classify the families of Lagrangian submanifolds determined by Cartan involutions.
2. General construction
The construction presented in this section is a more general version of the one given in [1], some proofs will have a lot of similarities, but here we will not be able to use some special structure such as compactness. In Section 2.1, we will see under what conditions the construction is identical to the one cited above.
Let G be a connected Lie group with Lie algebra g and take a representation ρ: G → Gl (V ) on a vector space V (with dim V < ∞). The infinitesimal representation of g on gl(V ) is also going to be denoted by ρ. The vector space V can be seen as an Abelian Lie group (or Abelian Lie algebra). In this way, we can take the semi-direct product G × ρ V which is a Lie group whose underlying manifold is the cartesian product G × V. This group is going to be denoted by G ρ and its Lie algebra g ρ is the semi-direct product
Our first purpose is to describe the coadjoint orbit on the dual g ∗ ρ of g ρ . To begin with, let’s see how to determine the ρ-adjoint representation ad ρ (X, v), where (X, v) ∈ g × ρ V . Thus, take a basis of g × V denoted by ℬ = ℬ g ∪ ℬ V with ℬ g = {X 1 , . . . , X n } and ℬ V = {v 1 , . . . , v d } basis of g and V , respectively. On this basis, the matrix of ad ρ (X, v) is given by
where ad (X) is the adjoint representation of g while for each v ∈ V , A (v) is the linear map g → V defined by
The dual space g ∗ ρ can be identified with g ∗ ⊕ V ∗ , where g ∗ is immersed on (g × V ) ∗ by extensions of linear functionals on g to g×V by the zero functional on V (in the same way, V ∗ is immersed on (g × V ) ∗ ). Therefore, the dual basis of B is B ∗ = B g ∗ ∪ B V ∗ , where B g ∗ and B V ∗ are the dual basis of B g and B V , respectively. Then, the coadjoint representation ad ∗ ρ (X, v), for (X, v) ∈ g ρ , with respect to B ∗ , is transposed with a negative sign on the off-diagonal term of (1), that is
In this matrix, ad ∗ is the coadjoint representation of g, ρ ∗ is the dual representation of ρ, that is
and A(v) ∗ : V ∗ → g ∗ is the transpose of A(v) for v ∈ V , which by the above equation can be seen as follows:
The adjoint representation ad ρ and coadjoint representation ad ∗ ρ of G ρ are obtained by exponentials of representations in g ρ . In particular, the following matrices are obtained (on the basis B and B ∗ ):
On the other hand, for g ∈ G the restriction of ad ρ (g) to V coincides with ρ (g) and the restriction of ad ∗ ρ (g) to V ∗ coincides with ρ ∗ (g), where we are seeing V and V ∗ as subspaces of g ρ = g ⊕ V and g ∗ ρ = g ∗ ⊕ V ∗ , respectively.
To describe the map A(v) ∗ , it is convenient to define the momentum map of the repre-sentation ρ.
Definition 2.1. The momentum map of the representation ρ is the map
given by
Then
because we have the following identifications
Lemma 2.2. The momentum map is G-equivariant, with respect to the representation ρ ⊗ ρ ∗ and the coadjoint representation, i.e., for g ∈ G, v ∈ V , and α ∈ V ∗
Proof. Let g ∈ G, note that the restrictions of ad ρ (g) and ad ∗ ρ (g) to V and V ∗ coincide with ρ(g) and ρ ∗ (g), respectively. Then, for X ∈ g
Since µ is bilinear, for any fixed α ∈ V ∗ , the map µ α : V → g ∗ given by µ α (v) = µ (v ⊗ α) is a linear map and consequently, its image µ α (V ) is a subspace of g ∗ . Let α ∈ V ∗ , the coadjoint orbit of G ρ through α will be denoted by
The following proposition shows that the coadjoint orbit for α ∈ V ∗ is the union of subspaces µ β (V ), with β ∈ ρ ∗ (G) α.
Proposition 2.3. For α ∈ V ∗ , the coadjoint orbit can be written as
and identifying g ∗ × V ∗ with g ∗ ⊕ V*
where β + µ β (V ) is an affine subspace of g ∗ ⊕ V ∗ .
Proof. Firstly, if g ∈ G we can identify ad ∗ ρ (g) with ρ ∗ (g) in the subspace V ∗ ⊂ g ∗ × V ∗ . Therefore, ρ ∗ (G) α ⊂ ad ∗ ρ (G ρ ) α, and as we saw before
which shows that if β ∈ V ∗ ⊂ g ∗ ⊕ V ∗ = g ∗ × V ∗ , then
which in terms of the momentum map is
Then, varying v ∈ V , we can see that the affine subspace β + µ β (V ) is contained in the coadjoint orbit of β, for β ∈ V ∗ . As ρ ∗ (G) · α ⊂ ad ∗ ρ (G ρ ) · α, we conclude that
Conversely, if g ∈ G and β ∈ V ∗
where the last equality is a consequence of the fact that µ is equivariant. For h ∈ G ρ , there are g ∈ G and v ∈ V , such that
As ad ∗ ρ e t(0,v) α ∈ α + µ α (V ), then ad ∗ ρ (h) α ∈ ρ ∗ (g) α + µ ρ ∗ (g)α (V ).
The action of G ρ is obviously transitive on G ρ · α, then it is an homogeneous space given by
the isotropy subgroup at α ∈ V ∗ ⊂ g ρ , with Lie algebra
Then in terms of the basis B ∗
therefore,
Thus
And
As T
α
(G
ρ
· α) ≈ g
ρ
/z
ρ
(α), for any (X, v) ∈ g
ρ
, there induced by (
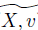) at ξ = β + µ
β
(w) ∈ G
ρ
· α (with β = ρ
∗
(g)α, g ∈ G, and w ∈ V ) given by
Hence
By Proposition 2.3, the coadjoint orbit G ρ ·α is the union of vector spaces and fibers over ρ ∗ (G) x of the representation ρ ∗ . This union is disjoint because given ξ ∈ (β + µ β (V )) ∩ (γ + µ γ (V )) then
with X, Y ∈ g. Since the sum g ∗ ρ = g ∗ ⊕ V ∗ is direct, it follows that β = γ and X = Y . Therefore there is a fibration
such that an element ξ = β + X ∈ β + µ β (V ) associates β ∈ ρ ∗ (G) α, and its fibers are vector spaces. The following proposition shows that this fibration can be identified with the cotangent space of ρ ∗ (G) α.
Let ϕ be the map
such that, for β ∈ ρ ∗ (G) α
This implies that the restriction of ϕ to a fiber β+µ β (V ) is given by a linear isomorphism
Theorem 2.4. The map ϕ is an isomorphism of vector bundles.
If ω is the KKS symplectic form on G
ρ
· α and ω is the canonical symplectic form on T
∗
(ρ (G) α), then ϕ is a symplectic isomorphism of vector bundles, i.e., ϕ
∗
The proof of this result has several steps, essentially they are as follows:
To see that: take ξ ∈ G ρ · α, there is a unique β ∈ ρ ∗ (G) α, such that ξ ∈ µ β (V ), then there is v ∈ V with ξ = β + µ (v ⊗ β). The vector v ∈ V defines a linear functional f v on V ∗ , and of course their respective restriction to T β (ρ ∗ (G) α), therefore f v ∈ T β ∗ (ρ ∗ (G) α). Set
A map ϕ is a linear injective map and the linear map µ (v ∧ w) →f v is surjective.
In the coadjoint orbit G ρ · α we can define the Konstant-Kirillov-Souriau (KKS) symplectic form, denoted by ω and defined as
where
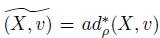is the Hamiltonian vector field of the function H
(X,v)
: M → R given by
Furthermore, as is known, for the cotangent bundle T
∗
(ρ
∗
(G) α) we can define the canonical symplectic form
The best way to relate these symplectic forms is through the action of the semi-direct product G ρ = G × V on the cotangent bundle of ρ ∗ (G) α. This action is described in Proposition 3.11 (in a general case), the action of G ρ on T ∗ (ρ (G) α) is Hamiltonian and then it defines a moment map
The construction of m shows that it is the inverse of ϕ. Moreover, m is equivariant, that is, it interchanges the actions on T ∗ (ρ (G) α) and the adjoint orbit, which implies that m is a symplectic morphism.
2.1. Compact case
Let U be a compact connected Lie group with Lie algebra u and take a representation : ρ U → Gl(V ), where V admits a U-invariant inner product h·, ·i when V is a real vector space (a Hermitian inner product when V is a complex vector space).
We will denote by U ρ the semi-direct Lie group U × ρ V , with Lie algebra u ρ = u × ρ V . The inner product allows us to identify V with V ∗ by
and we can also identify ρ with ρ ∗ by
Now, analogously to the discussion for the general case, we can characterize the coadjoint orbit of U ρ in terms of the momentum map µ: V ⊗ V → u ∗ given by
By construction, ρ(u) is an isometry for all u ∈ U with respect to the fixed U-invariant inner product, then ρ(X) is a skew-symmetric linear map with respect to {.,.} for all X ∈ u, and we have
that is, µ is skew-symmetric. Therefore, the momentum map µ is defined in the exterior product ∧ 2 V = V ∧ V . Furthermore, the compact Lie algebra u admits an ad-invariant inner product such that we can identify u ∗ with u, then
Similarly, the dual u ∗ × V ∗ of u ρ = u × V is identified by its inner product which is a direct sum of ad-invariant inner products of u and V . In that identification, the coadjoint representation of u can be seen as the adjoint representation of u because its inner product is u-invariant, but the inner product of V is not invariant under the adjoint representation of V , then the coadjoint representation of that Abelian algebra is the transpose of its adjoint representation. This means that the coadjoint representation of u × V is written in u × V as type matrices on orthonormal bases:
where for each v ∈ V , A (v) : V → u can be identified by A (v) (w) = µ (v ∧ w).
Then the representations ad ρ and ad ∗ ρ of U ρ are obtained by exponentials of representa-tions in u ρ , take v ∈ V ⊂ u × V and by Proposition 2.3
2.2. Examples
We will see some examples of semi-direct coadjoint orbits to compare them with the usual orbits. To begin with, take ρ the canonical representation of u = so (n) in V = (ℝ n , h·, ·i). The momentum map with values in u is given by
and as we know the invariant inner product on so(n) is
To describe the orbit, take the isomorphism I: ∧ 2 V → so (n) given by
which satisfies
If A ∈ so(n) we have
Let {e 1 , . . . , e n } be an orthonormal basis of V , then
Therefore identifying V
∗
with V by h·, ·i, and so(n)
∗
with so(n) by
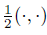, the momentum map is µ(v ∧ w) = I(v ∧ w), that is
For simplicity of notation, we will denote I(w ∧ v) for v, w ∈ V as v ∧ w. If v and w are n × 1 column vectors, we have
which is an n × n matrix.
As we saw above, the coadjoint representation of so(n) × ρ ℝ is given by
where for each v ∈ ℝ n , A (v) : ℝ n → so (n) is the map
The representation so (n) ρ ℝ n defines a representation of the semi-direct product U ρ = SO(n) ρ ℝ n on so (n) ℝ n by exponentials (here so (n) ℝ n is the space where the U ρ -orbit is being identified). As discussed earlier a U ρ -orbit of v 2 ℝ n so (n) ℝ n is given by
In this case, the orbits of SO (n) in ℝ n are the (n − 1)-dimensional spheres centered at the origin.
Example 2.5. For n = 2, we have that so (2) x ρ ℝ2 is isomorphic with ℝ3 and for all w 2 ℝ2 the image A(w) ℝ2 = so (2), therefore the coadjoint semi-direct orbits are the circular cylinders with the axis on the line generated by so (2) in so (2) ℝ2 ≈ ℝ3 .
Let h be a subalgebra of so(n). We can induce the canonical representation of h in ℝ n as a restriction on so(n), then
because the inner product of ℝ n is invariant by h. The trace form −tr AB provides (by restriction) an inner invariant product in h, that allows us to identify h with h ∗ .
Let p: so(n) → h be the orthogonal projection in relation to the trace form. By the identification above of h ∗ and h we can define the h-momentum map
where µ is the momentum map of so(n). Then
For u(n), we can take a canonical representation in ℂ n = ℝ 2n and see u(n) as an immersed subalgebra of so(2n) by matrices 2n × 2n of the form
Then h = u(n) and p: so(2n) → u(n) is the orthogonal projection with respect to the trace form. Hence the momentum map is
3. Coadjoint semi-direct orbit given by a Cartan decomposition
In this section, we will see the results of Section 2 in the structure of any semisimple non-compact Lie algebra, determined by a given Cartan decomposition. This structure was studied and described in [1], where the authors made the following: Let g be a non-compact semisimple Lie algebra with Cartan decomposition g = ŧ ⊕ s. As [ŧ, s] ⊂ s, the subalgebra ŧ can be represented on s by the adjoint representation. Then, we can define the semi-direct product ŧ ad = ŧ × s, where s can be seen as an Abelian algebra. This is a new Lie algebra structure on the same vector space g where the brackets [X, Y ] are the same when X or Y are in k, but the bracket changes when X, Y ∈ s. The identification between ŧ ad = ŧ × s and its dual ŧ ∗ ad = ŧ ∗ × s ∗ is given by the inner product B θ (X, Y ) = −hX, θY i, where h·, ·i is the Cartan-Killing form of g and θ is a Cartan involution. If A ∈ ŧ, then ad (A) is anti-symmetric with respect to B θ , while ad (X) is symmetric for X ∈ s. The moment map is given by
the second part of that equality is
because [X, Y ] ∈ ŧ. Therefore the moment map of the adjoint representation of ŧ on s is
where [·, ·] is the usual bracket of g. Therefore, the coadjoint representation of the semi-direct product ŧ × s is given by (in an orthonormal basis)
where for each Y ∈ s, A (Y ) : s → k is the map A (Y ) (Z) = [Y, Z].
Let G be a connected semisimple Lie group with Lie algebra g and take K ⊂ G the subgroup given by K = {exp k ŧ }. The semi-direct product of K and s will be denoted by
The coadjoint orbit of x̅ ∈ s ⊂ ŧ ×s is the union of the fibers A (Y ) (s) with Y belonging to e the K-coadjoint orbit of X in s. As A (Y ) (Z) = [Y, Z], then A (Y ) (s) = ad (Y ) (s) where ad is the adjoint representation in g. To detail the coadjoint orbits of the semi-direct product, take a maximal Abelian subalgebra a ⊂ s. The ad (K)-orbits in s are passing through a are thus the flags on g. Take a positive Weyl chamber a+
⊂ a. If H ∈ cl (a +) then the orbit ad (K) H is the flag manifold
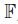H
. By Proposition 2.4, the K
ad
-orbit in H ∈ cl(a+) is diffeomorphic to the cotangent bundle of
H
, thus the K
ad
-orbit itself is the union of the fibers ad (Y ) (s), with Y ∈
H
. In conclusión
In this union, the fiber over H is H + ad (H) (s) with ad (H) (s) ⊂ ŧ. With the notations above this subspace of k is given by
3.3. Hermitian symplectic form and Lagrangian submanifolds
Let gC be a complex semisimple Lie algebra and u its compact real form with Cartan involution τ, such that
is a Hermitian form of gC, where h·, ·i C is the complex Cartan-Killing form of gC.
Remark 3.1. To avoid confusion, we have that gℂ is the complexification of g (or realifi-cation for gℝ), the complexification will be denoted at the top. While gℂ will simply be to indicate that it is complex (or real for gℝ) , this is will be denoted at the bottom.
The imaginary part of ℋ τ will be denoted by Ω τ , which is
is a symplectic form on gC (see [13]) and will be called the symplectic Hermitian form determined by τ.
Let G be a connected Lie group with Lie algebra gC. For that, let gC = u ⊕ iu be a Cartan decomposition with Cartan involution τ, for g a semisimple complex Lie algebra. If U ⊂ G is the compact subgroup with Lie algebra u. Then, we will denote by U ad its respective semi-direct product (described in Section 3 for the general case).
If H ∈ s = iu, then its semi-direct orbit is denoted by U ad · H, given by
Remark 3.2. Without loss generality, we can choose H ∈ a or H ∈ cl(a+), where a ⊂ s is the maximal Abelian subalgebra of g, or a+ their respective positive Weyl chamber (see [12] and [13]).
In [1] it was proved that the form Ω τ of g restricted to U ad · H is a symplectic form, for H ∈ cl(a+) and the following theorem:
Theorem 3.3. The manifolds (U ad · H, Ω τ ) and (ad(G) · H, Ω τ ) are symplectomorphic.
3.4. Lagrangian families
Let g be a real semisimple non-compact Lie algebra, such that is a real form of gC, and u a compact real form of gC with Cartan involution τ (i.e., g and u are real forms of gℂ). Then
is a Cartan decomposition of g.
Lemma 3.4. The restriction of H τ to g is real.
Proof. For X, Y ∈ g, there are X 1 , Y 1 ∈ g ∩ u and X 2 , Y 2 ∈ g ∩ iu such that X = X 1 + X 2 and Y = Y 1 + Y 2. Then
As we have that
where ·{.,.}·i ℂ is the Cartan-Killing form of gℂ, then
However
as H
τ
is an Hermitian form, we have that
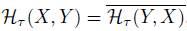, thus,
and by equation (11), we have that
but X 1 , Y 1 , iX 2 , iY 2 ∈ u, and the restriction of {.,.}·i ℂ to u is negative-definite, we can conclude that H τ | g is real.
Corollary 3.5. Ω τ | g ≡ 0.
Moreover, let G ℂ be a Lie group with Lie algebra gℂ. Therefore, given any submanifold M of U ad · H, M must be contained on g. In fact, M is an isotropic submanifold of U ad · H. By Theorem 3.3 the same applies to any submanifold M of ad r (G ℂ) · H.
Remark 3.6. To avoid confusion, in this subsection, we say G ℂ to specify that this is a complex Lie group with Lie algebra gℂ.
Now, our purpose is to apply the last results for a non-trivial immersion on the coadjoint semi-direct orbit to find some Lagrangian submanifolds. With the Cartan decomposition of g given in (10), then
Take K = {exp kŧ}, then K ad · H is an immersed submanifold on U ad · H, for H ∈ a. Moreover,
where ŧ ad can be identified with g as a vector space and by Corollary 3.5, the restriction of H τ to g is real, thus,
Therefore, K ad · H is an isotropic submanifold of U ad · H, we want to see that K ad · H is a Lagrangian submanifold of U ad · H, as we can see in the following example.
Example 3.7. For g = sl(2, ℝ), k = so(2), and u = su(2). Given
we have that K ad · H (cylinder) is a 2-dimensional isotropic submanifold of U ad · H, a 4-dimensional manifold.
Hence, the cylinder K ad · H is a Lagrangian submanifold of U ad · H.
Let σ be an anti-linear involutive conjugation on gC, such that g is the subspace of fixed points of σ, that is
If we have that A: = {X ∈ U ad · H: σ(X) = X} coincides with K ad · H, then we can conclude that K ad · H is a Lagrangian submanifold of U ad · H, with respect to the Hermitian symplectic form, for H ∈ a.
As K ad ·H is contained on g and it is a submanifold of U ad ·H, we have that K ad ·H ⊆ A. For the opposite inclusion, by equation (8) we have that
then given an element x ∈ U ad · H implies that
As u = k ⊕ is, we have the following possibilities:
if Z 2 ŧ, we have that σ(Z) = Z and if Z 2 is, we have that σ(Z) = -Z, then σ(x) = x if and only if Z 2 is.
Thus, x is a fixed point if and only if x 2 K ad H.
for Z ∈ u, we have that σ(x) =6 x, then in this case it is impossible to have fixed points.
For any other possible choice of X ∈ u, we do not have fixed points because it would be a combination of the cases above.
Therefore, A = K ad · H and K ad · H is the set of fixed points of σ, its dimension is half the dimension of U ad · H. Hence,
Proposition 3.8. For H ∈ a, the coadjoint orbit K ad · H is a Lagrangian submanifold of U ad · H, with respect to the Hermitian symplectic form.
By Theorem 3.3, the K ad -coadjoint orbit is symplectomorphic to G-adjoint orbit and U ad -coadjoint orbit is symplectomorphic to G ℂ -adjoint orbit, with respect to Ω τ . Then, we can conclude that
Corollary 3.9. For H ∈ a, the orbit ad(G) ·H is a Lagrangian submanifold of ad(G ℂ) ·H, with respect to the Hermitian symplectic form.
Furthermore, the coadjoint orbit U ad · H is invariant by the automorphism of u, because any automorphism of u leaves invariant its Cartan subalgebra (see [12] or [14]). Given k ∈ Aut(k) we know that the k-action on g leaves invariant the Cartan decomposition of g, its maximal Abelian subalgebra and u (because k is contained in u). If exp is the exponential between the Lie algebra u and the Lie group Aut(u), then for any X ∈ is we have that g tX = exp(tX) · g is a real form of gℂ with Cartan decomposition g tX = ŧ tX ⊕ s tX . Take G tX a Lie group with Lie algebra g tX ⊂ u, then we can conclude that.
Theorem 3.10.
For X ∈ is ⊂ u, there are a Lagrangian family of submanifolds {M
tX
} on ad(G
ℂ )·H with respect to the Hermitian symplectic form. For t ∈ I, M
tX
= ad(G
tX)·
.
In fact, the family of Lagrangian submanifolds is determined by g, and given by the is-conjugated real forms of g.
