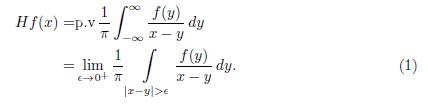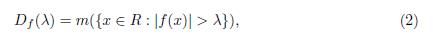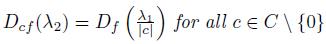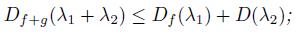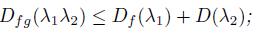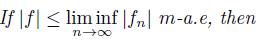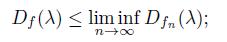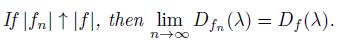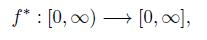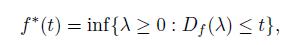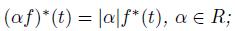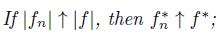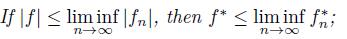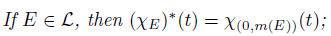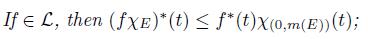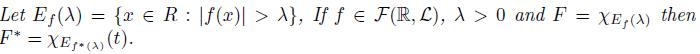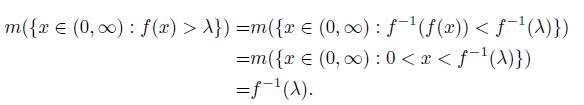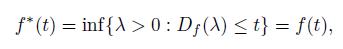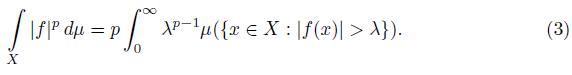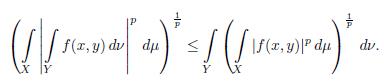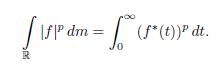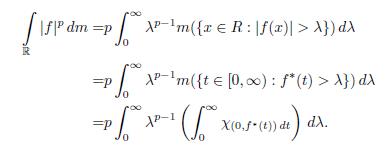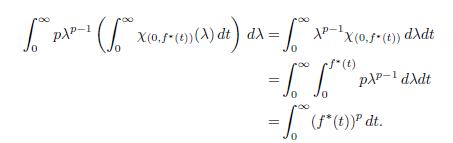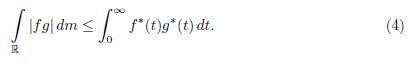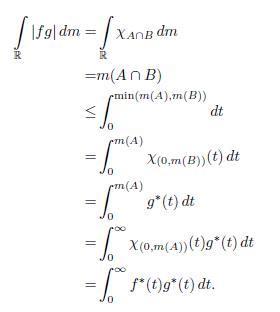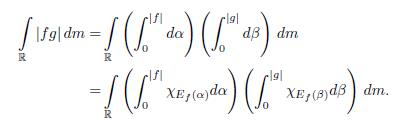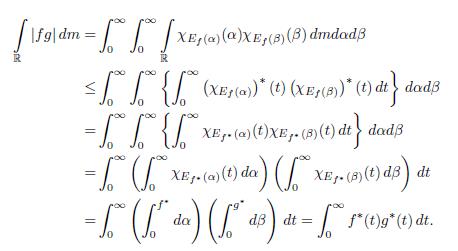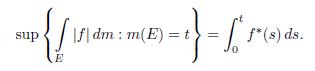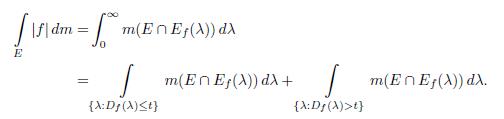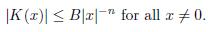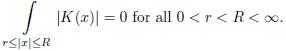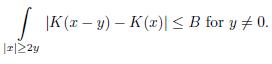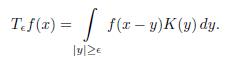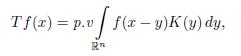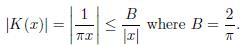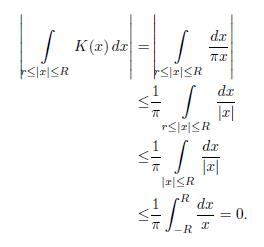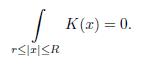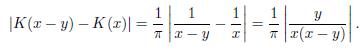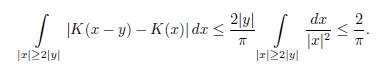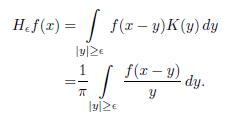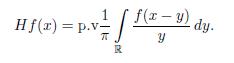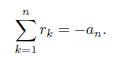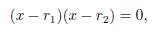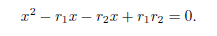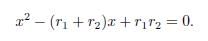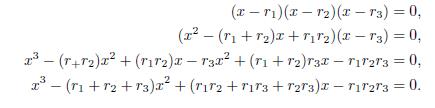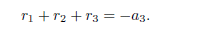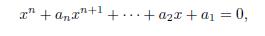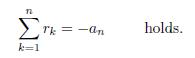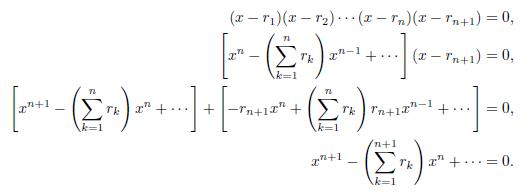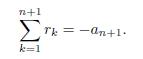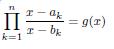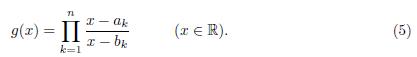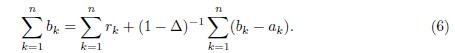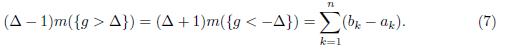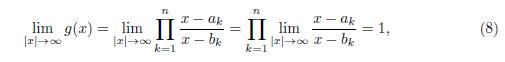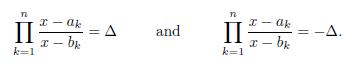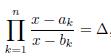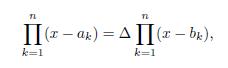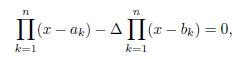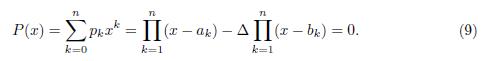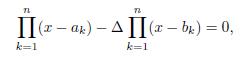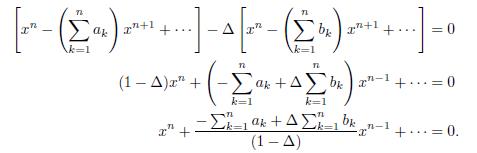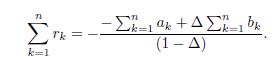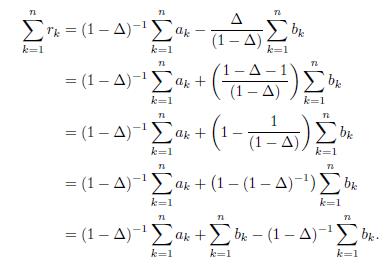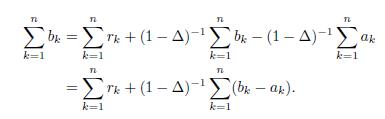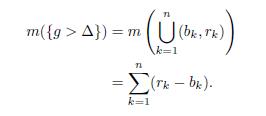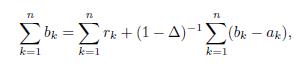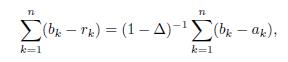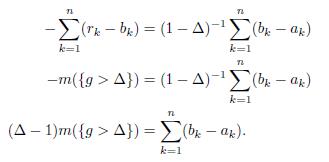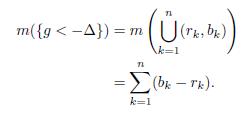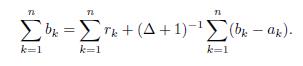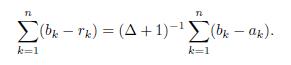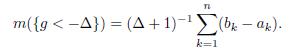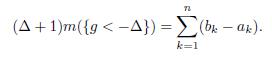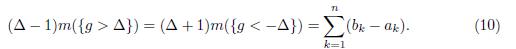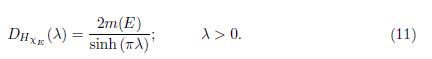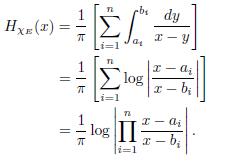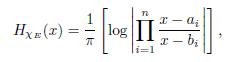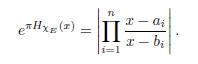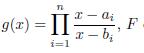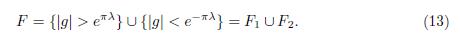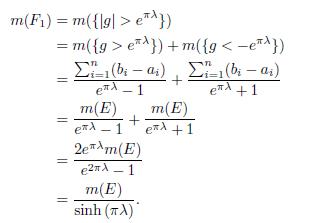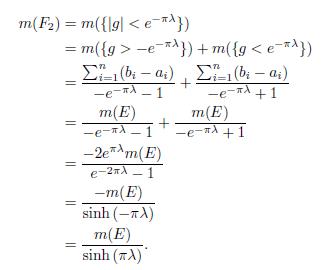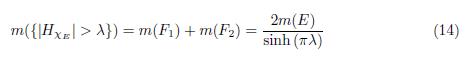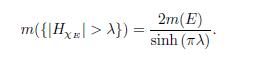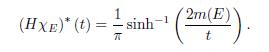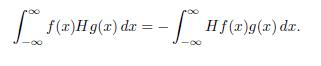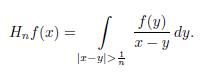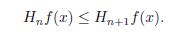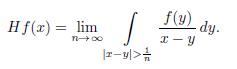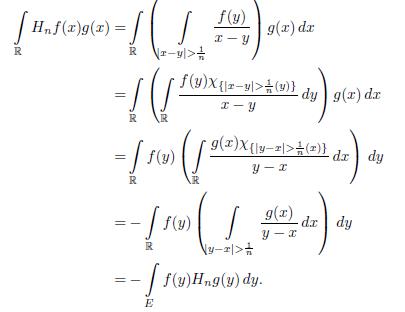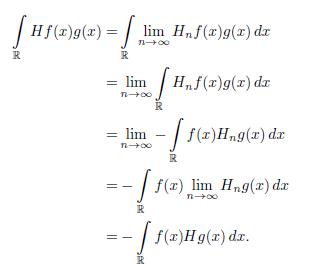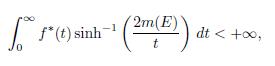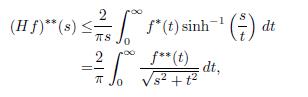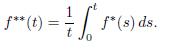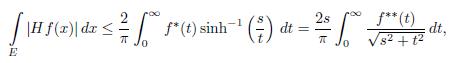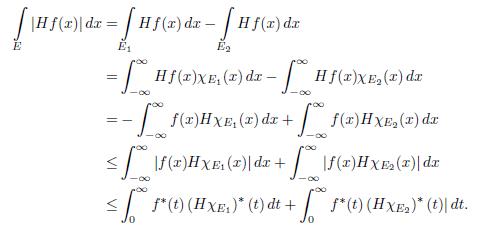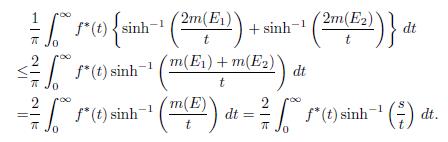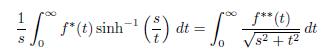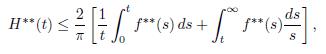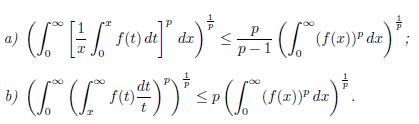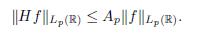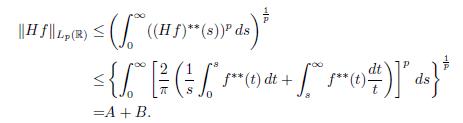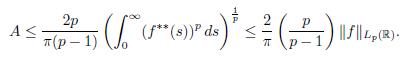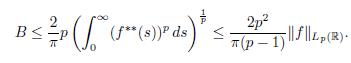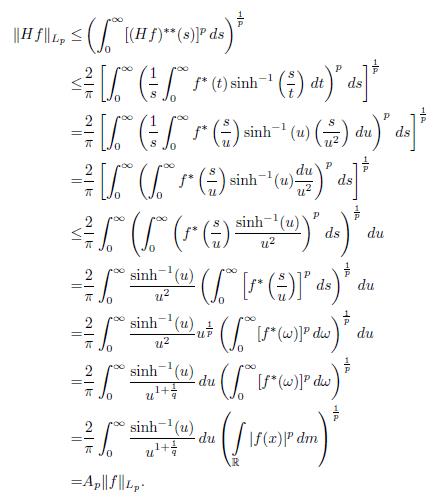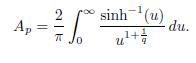1.The Hilbert transform

The Hilbert transform of a sufficiently well-behaved function f(x) is defined to be

The central idea behind the definition of transform is quite simple, namely to transform f(x) by convolving it with the kernel 1πx. It is doing so rigorously that one finds technical difficulties, the kernel fails to be absolutely integrable due to its slow decay and more importantly, due the singularity at the origin. The limiting argument in (1) is used to avoid the singularity by truncating the kernel around the origin in a systematic fashion. The aim of this review is to address the L_p-boundedness of H. We provide this analysis in Section 4. Now, we are going to provide some references about further aspects of the theory of singular integrals.

The theory of singular integrals has its roots in the works of Calderón and Zygmund [³] and Mihlin [¹⁵]. The Hilbert transform is a fundamental example in the theory of singular integrals. Two celebrated results about the boundedness properties of H can be remarked: the L_p-boundedness result of H due to M. Riesz, and the weak-(1; 1) boundedness of H, due to Kolmogorov. For the general aspects of the theory of singular integrals as well as the modern developments about the theory of pseudo-differential operators, which are important generalizations of the singular integrals, we refer the reader to [⁷, ⁸, ¹¹, ¹², ¹⁷]. For a substantial treatment about the subject we refer the reader to [¹⁴], and for a concise review on the subject we refer to [⁹].

This paper is organized as follows. In Section 2 we present some preliminaries dedicated to the rearrangements of functions. In Section 3, we present the definition of Calderón-Zygmund operators and we motivate the Hilbert transform as a fundamental example of this definition. Finally, in Section 4, we make a review of the L_p-boundedness of the Hilbert transform.

2. Preliminaries

Let us begin by presenting some definitions and properties regarding to the decreasing re-arrangement. As usual (ℝ; ℐ; m) stand for the one-dimensional Euclidean space endowed with the Lebesgue measure and F(ℝ; ℐ) denote the set of all ℐ-measurable functions on R.

Definition 2.1. The distribution function D_f of a function f 2 F(ℝ; ℐ) is given by

for all λ ≥0.

Observe that the distribution function D_f depends only on the absolute value of the function f and its global behavior. Moreover, notice that D_f may even assume the value +∞.

It should be pointed out that the notation for the distribution function in (2) is not standard, other authors use the notations f_*, μ_f, d_f , λ_f , among others.

The distribution function D_f enjoy the following properties.

Theorem 2.2. Let f and g be two functions in F(ℝ; L). Then for all λ₁; λ ₂; λ ₃ ≥ 0 we have:

a)D_f is decreasing and continuous from the right;

b) |g| ≤ |f| m-a.e implies that D_g(λ) ≤ D_f (λ);

c)

d)

e)

f)

g)

For the proof of all this properties see [⁶, ⁵].

With the notation of the distribution function we are ready to introduce the decreasing rearrangement function and its important properties.

Definition 2.3. Let f 2 F(ℝ; ℐ). The decreasing rearrangement of f is the function

defined by

taking the usual convention that inf(∅)= 1.

The next theorem establishes some basic properties of the decreasing rearrangement function.

Theorem 2.4. The decreasing rearrangement function has the following properties:

(a) f^* is decreasing;

(b) f* (t) > λ if and only if D_f (λ) > t;

(c) f and f* are equimeasurable, that is D_f (λ) = D_f* (λ) for all λ ≥ 0;

(d)

(e)

(f)

(g) For 0 < p < ∞, (|f|^p)^* (t) = [f* (t)]* ;

(h) If |f| ≤ |g|, then f*(t) ≤g*(t);

(i)

(j) ^.

(k)

For the proof of all these properties see [⁶, ⁵]. The next result tells us that a function cannot have two different decreasing rearrangements, see [⁶] and also [⁵, Theorem 1.8].

Theorem 2.5. There exists only one right-continuous decreasing function f equimea-surable with f.

For a positive strictly decreasing function f, it is itself its decreasing rearrangement, as the next result shows.

Theorem 2.6. Let f be a strictly decreasing and non-negative function on (0; 1) then f (t) = f(t).

Proof. Consider

Take t = f ^-1(λ) then λ= f(t). Thus

that is f (t) = f(t), as we claim. The proof of Theorem 2.6 is complete.

The following theorem is quite important since it allows us to calculate an integral in a general space via an one-dimensional integral. The formula (3) below is sometimes called the Cavalieri principle.

Theorem 2.7. Let (X; A, μ) be σ -finite measure space and let f be anA-measurable function. Then

For the proof of this statement we refer to [⁶]. The next theorem, known as Minkowski integral inequality, will be useful in proving latter results in this paper.

Theorem 2.8 (Minkowski integral inequality). Let (X; A₁; ) and (Y;A₂, v) be σ-finite measure spaces. Suppose that f is aA₁A₂ -measurable function and f( ; y) Є L_p(μ) for all y Є Y . Then for 1 ≤p ≤1 we have

For the proof of this statement see [⁶]. A function and its decreasing rearrangement has the same L_p-norm. Indeed, we have the following L_p-identity.

Theorem 2.9. Let f Є L_p(ℝ), 1 ≤p < ∞. Then

Proof. By Theorem 2.7 and Theorem 2.4 (c), we have that

Next, by applying the Fubini theorem, we have that

The proof is complete.

The following inequality is due to Hardy and Littlewood.

Theorem 2.10. If f and g, both belong to F(ℝ; ℒ), we have the identity

Proof. Assume first that f =x_A and g =x_B are characteristic functions where A and B are sets in ℒ. We suppose without loss of generality that m(A) and m(B) are finite. Then it follows from Theorem 2.4(i) that

In general let f and g be two functions belonging to F(ℝ; ℒ). Then

It follows from Fubini’s theorem and Theorem 2.4 (h) and the property (k) of this theorem that

The proof is complete.

Theorem 2.11. Let f Є L₁(ℝ). Then

Proof. Given the real number t > 0, we have that

The following is a well known fact from the measure theory: if m(E_f (λ)) > t > 0, then there exists a set E Є ℒ such that E ⊆ E_f (λ) and m(E) = t. Hence

The proof is complete.

3.Calderon-Zygmund singular integral operators

Taking into account the Calderón-Zygmund theory we are going to have the Hilbert transform as a fundamental example. We recall the following definition.

Definition 3.1. Suppose that K(x) 2 L_loc(ℝⁿ∖{0}) and satisfies the following conditions:

(a)

(b)

(c)

A kernel as in Definition 3.1 is called the Calderón-Zygmund Kernel where B is a constant independent of x and y. The condition (c) is called Hörmander condition..

Now, we present the following fundamental theorem.

Theorem 3.2. Suppose that K is the Calderón-Zygmund kernel. For > 0 and f 2 L_p(ℝⁿ), 1 < p < 1, let

Then the following statements holds:

(1) ||T_Є f||_Lp ≤ A_p||f||_Lp where A_p is independent of and f.

(2) For any f 2 L_p(ℝⁿ), lim T_Є f exists in the sense of the L_p -norm. That is, there exists an operator T such that

holds for almost every x Є ℝⁿ .

In addition, one can show that K(x) = 1πx, that is, the kernel of the Hilbert transform satisfies the hypothesis in Theorem 3.2. We prove that it satisfies the properties in Definition 3.1 below. Note that

(a)

(b)

Since 1x is an odd function, we have

Note that

Now, if . Indeed

Consequently,

Hence K(x) = 1πx is a Calderon-Zygmund kernel. Now, let us define

By Theorem 3.2, we have that

So we might say roughly that Hilbert’s transformation of a function f is the convo-lution of f with the Calderón-Zygmund kernel K(x) = 1πx.

4. A theorem due to E. M. Stein and G. Weiss

This section is based on [¹, ⁴]. The following lemmas will be helpful for the proof of Theorem 4.3. We present these lemmas and their proofs below.

Lemma 4.1. Let P (x) = xⁿ + a_nx^{n +1} + + a₂x + a₁ be polynomial of degree n. Let r₁; r₂; ; r_n be the roots of P (x) = 0, then

Proof. The proof uses the mathematical induction. When n = 2, the polynomial x² + α₂x + α₁ = 0 has two roots, r₁ and r₂, such that

then

In consequence

Hence r₁ + r₂ = α₂. Now, for n = 3, the polynomial x³ + α₃x² + α₂x + α₁ = 0 has three roots named r₁; r₂ and r₃ such that

From this last equality we have that

Next, suppose that for

the property

Now, the polynomial xⁿ⁺¹ + α_n+1xⁿ + + α₂x + α₁ = 0, has n + 1 roots r₁; r₂; ; r_n+1 such that

Therefore

The proof of Lemma 4.1 is complete.

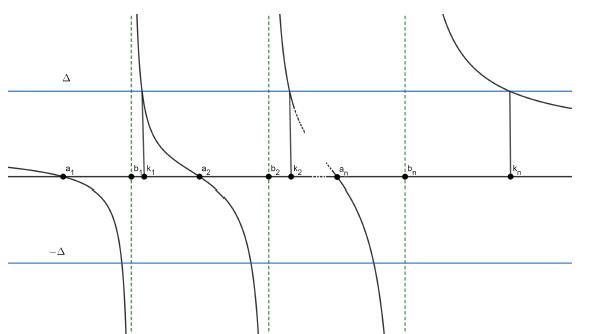
Lemma 4.2. Suppose that α_i , b_i (i = 1; 2; 3; …, n) are real numbers satisfying that α₁ < b₁ < α ₂ < b₂ < … < a_n < b_n and let g be the rational function

If Δ # 1, then the equation g(x) = |Δ| has n different roots r₁; r₂; ; r_n which satisfy that

Furthermore, if Δ > 1, then

Proof. Since g has a simple pole at each b_k, (k = 1; 2; 3; …,n) and

there are exactly n different solutions, say r₁; r₂; ; r_n to the equation g(x) = |Δ| (Δ # 1). Then

For , we have that

and so

Where

Then

Which implies that

Since r₁; r₂; ; r_n are the roots of the polynomial P (x) = 0, then by Lemma 4.1 we have that

In consequence,

Hence

If Δ > 1, then 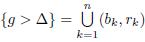(see figure 1) and so

Since

we have that

and putting these equations together we have that

Moreover, if 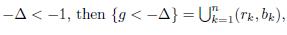(see figure 1). Hence

Now, we have

Also,

In consequence

Finally,

In view of the analysis above, we conclude that

The proof of Lemma 4.2 is complete.

In the following result we can observe that the distribution function of H _E depends only on the measure of E and not on the way in which E happens to be distributed over the real line.

Theorem 4.3 (Stein-Weiss [¹⁹]). Let E be the union of finitely many disjoint intervals, each of finite length. Then

Where D_HxE (λ) = m({|H_xE| > λ).

Proof. We may express the set E in the form

where α₁ < b₁ < α ₂ < b₂ < < α _n < b_n. We already know that

Fix λ > 0, and let F = {|H_xE| > λ}. Then m(F ) = D_HxE (λ). Since

we have that

If we set can be decompose as

Now, by applying Lemma 4.2 to g we obtain,

Next, for F₂, we have that,

Finally

i.e.

The proof of Theorem 4.3 is complete.

A short proof of the Stein-Weiss theorem using complex-variable methods can be found in Calderón [²] and Garnett [¹³]. Also, an additional discussion can found in Sagher and Xiang [¹⁸]. The Stein-Weiss theorem has been discussed for the ergodic Hilbert transform by Ephremidze [¹⁰]. As a corollary of Theorem 4.3, given that f is essentially the inverse function of D_f (λ), we compute (H_xE)^* (t) as follows.

Corollary 4.4. Let E ⊆with m(E) < ∞. Then

The next theorem shows that the operator H is anticommutative.

Theorem 4.5. Let f Є L_p(ℝ) and g 2 L_q(ℝ) (1 < p < ∞). Then

Proof. Let us start by defining

Note that

Consequently,

An application of Fubini Theorem gives

Finally by the monotone convergence Theorem we have that

The proof is complete.

The following result, due to O’Neil, provides a bound of (Hf)^** . We provide a proof with enough details.

Theorem 4.6 (O’Neil-Weiss [¹⁶]).

The function Hf(x) exists almost everywhere and for each s > 0 one has that

where

Proof. By Theorem 2.11, the statement will be established if we can show

for each set E of measure s, that is m(E) = s.

Given such a set, let E₁⊂E be the subset where Hf(x) ≥ 0 and let E₂ = E/E₁. Using Theorem 2.10, Corollary 4.4 and Theorem 4.5 we have that

By Corollary 4.4, the previous expression is equal to

So the desired inequality holds. The equality

follows by integration by parts. The proof of Theorem 4.6 is complete.

Corollary 4.7 (O’Neil-Weiss’s Inequality). Let f be a measurable function on (-∞;∞). Then

for each t > 0.

We shall need the following form of the Hardy inequality (see [⁶]).

Lemma 4.8. If p > 1 and f is a nonnegative function defined on (0, ∞). Then:

Now we present a theorem due to M. Riesz.

Theorem 4.9 (M. Riesz Theorem). If 1 < p < ∞ and f Є L_p(ℝ). Then there exists A_p independent of f 2 L_p(ℝ) such that

Proof. By Corollary 4.7 we have that

Now, by Lemma 4.8(a), we have that

And by part (b) of Lemma 4.8 we have that

The analysis above shows the theorem.

We can also give another proof of Theorem 4.9 using Minkowski’s integral inequality, as it is shown below. The proof is due to O’Neil-Weiss [¹⁶].

Proof. By making an appropriate change of variables and by employing Minkowski’s integral inequality (see Theorem 2.8), we have that

Thus we proved Theorem 4.9 with