Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.28 no.1 Bogotá Jan./Apr. 2008
Libardo Andrés González Torres1, Diego Alexander Garzón-Alvarado2 y Máximo Alejandro Roa Garzón3
1 Ingeniero mecánico. Estudiante, M. Sc. en Matemática Aplicada y Ph.D. en Mecánica computacional, Universidad de Zaragoza, España. Grupo de Modelado y Métodos Numéricos en Ingeniería, GNUM. landresg@unizar.es
2 Ingeniero mecanico. M.Sc., en Ingeniería Mecánica, Universidad de Los Andes, Colombia. M.Sc., en Materiales y Procesos de Manufactura, Universidad Nacional de Colombia, DEA Universidad de Oviedo. Ph.D., en Mecánica Computacional, Universidad de Zaragoza. España. Profesor asociado, Universidad Nacional de Colombia. Grupo de Modelado y Métodos Numéricos en Ingeniería, GNUM. dagarzona@bt.unal.edu.co
3 Ingeniero mecánico. Especialista, en astronomía. M.Sc., en Automatización Industrial. Ph.D., en Robótica. Profesor Asistente, Universidad Nacional de Colombia, Bogotá. Grupo de Modelado y Métodos Numéricos en Ingeniería, GNUM. maroag@unal.edu.co
RESUMEN
El objetivo del presente artículo se enmarca en la revisión de la teoría y la implementación numérica de uno de los métodos numéricos sin malla usados para la solución de problemas de tipo estructural, el método de los elementos naturales (MEN), junto con la contrastación de los resultados obtenidos para dos problemas estructurales elástico-lineales en dos dimensiones con la solución analítica exacta y la aproximada por el método de los elementos finitos (MEF). Se describe la técnica de interpolación usada por el MEN para obtener las funciones de forma y se presentan las características más importantes del método en su forma estándar. Se presentan los resultados de dos simulaciones de problemas estructurales realizadas usando un código escrito en Matlab 6.5 para la solución de ecuaciones diferenciales de elasticidad lineal en dominios bidimensionales. Se concluye que el método de los elementos naturales es similar al de los elementos finitos en cuanto a estabilidad y convergencia, con la ventaja de que la malla es generada automáticamente y la no dependencia de la solución aproximada con la distribución de la nube de puntos que define la geometría.
Palabras clave: métodos sin malla, método de elementos naturales, método de elementos finitos, interpolación por vecinos naturales.
ABSTRACT
This paper was aimed at reviewing the theory and numerical implementations of the natural elements method (NEM, meshless method) used for resolving structural problems. An exact analytical solution and the finite element method were used for comparing the results obtained for two lineal-elastic structural problems in two spatial dimensions. The interpolation procedure used by the method for obtaining the trial functions and the most important features of the standard NEM are described. The results of two simulations concerning structural problems are presented using a code written in Matlab 6.5 for resolving differential lineal elasticity equations in two dimensional domains it was found that NEM is similar to the finite element method in terms of stability and convergence, having the advantage of mesh being automatically produced and the approximated solution not depending on the distribution of the node cloud, thereby defining the geometric domain.
Keywords: meshless method, natural element method, finite element method, natural neighbour interpolation.
Recibido: diciembre 7 de 2006
Aceptado: noviembre 20 de 2007
Introducción
Existen numerosos métodos numéricos en ingeniería que permiten solucionar problemas estructurales, de mecánica de fluidos, de transferencia de calor, etc., satisfactoriamente, sin importar la linealidad del modelo o la complejidad de la geometría. El de los elementos finitos, de diferencias finitas, y los espectrales, son solo una muestra de los diferentes métodos numéricos usados para la solución de ecuaciones diferenciales de ingeniería (Dunn et al., 2006; Ollivier-Gooch, 2003; Coz Diaz et al., 2007; Prabhakar y Reddy, 2006; Griffiths, 1991).
Generalmente estos métodos necesitan de una malla bien definida que debe cumplir ciertos requisitos de regularidad y de forma (Cueto, 2001; Sukumar,1998). Desde hace ya varios años se han venido desarrollando algunos conocidos como métodos sin malla (Cueto, 2003; Doblare et al., 2005), que disminuyen las restricciones sobre las mallas que deben ser usadas para la solución de las ecuaciones en el dominio de interés, o que permiten la definición de la geometría desde una nube de puntos, a través de la cual se determina la malla automáticamente (Pena et al., on line, 2008). El método de los elementos naturales (MEN) es un representante de este grupo y se caracteriza por ser una técnica interpolante (es decir la superficie de solución pasa por los valores nodales de la variable aproximada), a diferencia de otros métodos sin malla en los que se calculan los valores nodales de la variable incógnita, pero la superficie de solución aproximada no pasa por estos valores nodales (Cueto, 2003; Doblare et al., 2005). En los últimos años el MEN ha sido usado en un sinnúmero de aplicaciones de ingeniería (como se puede ver en (Cho y Lee et al., 2007; Hajri et al., 2007; Alfaro et al., 2006)), en la Figura 1 se puede apreciar un ejemplo de la aplicación del método para la aproximación de la distribución de temperaturas a lo largo del tiempo en un proceso de extrusión de un perfil de aluminio.
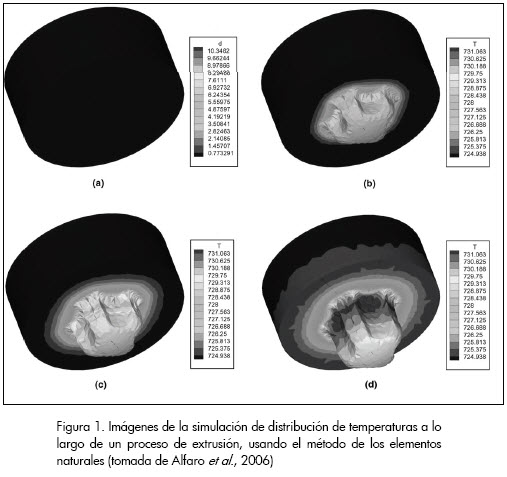
Método de elementos naturales
En el método de los elementos naturales (MEN) las funciones de forma son definidas a partir de un tipo de interpolación conocida como âinterpolación por vecinos naturalesâ, la cual a su vez se define a partir del diagrama de Voronoi o su dual, la triangulación de Delaunay (Cueto, 2001; González et al., 2006), como se indica enseguida.
Diagrama de Voronoi y triangulación de Delaunay
El diagrama de Voronoi o su dual, la triangulación de Delaunay, es una de las construcciones más usadas para definir un conjunto irregular de puntos o nodos (Sukumar, 1998). Aquí se presentará, por simplicidad y teniendo en cuenta los alcances del documento, la definición de estos diagramas en el espacio R2, pero es posible extenderla a un espacio Rn.
Un diagrama de Voronoi es una agrupación de celdas (Figura 2) definidas para una distribución dada de puntos N = {n1, n2,⦠nI,â¦nM}, que determinan una región en el espacio R2. Cada una de estas celdas, por ejemplo la TI, es una región dentro de la cual cualquier punto x perteneciente a ella es más cercano al nodo nI que a otro nodo, nJ, (con Jâ I). El nodo nI es llamado âel vecino más cercanoâ del punto x. Una definición matemática formal para la celda de Voronoi de primer orden es la siguiente:
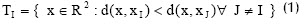
en donde d(xI, xJ), es la distancia euclidiana entre xI y xJ.
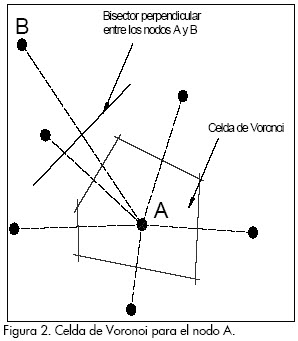
El dual del diagrama de Voronoi, una construcción geométrica que contiene la misma información, es conocido como la triangulación de Delaunay, que puede ser determinada uniendo los nodos cuyas celdas de Voronoi compartan alguno de sus lados; la Figura 3 muestra un ejemplo de esta triangulación.
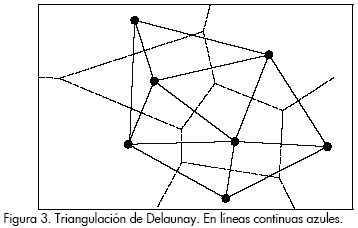
La triangulación de Delaunay puede ser vista como una red de triángulos que cumple la condición de Delaunay (denominada así por el matemático ruso Boris Nikolaevich Delon, quien la inventó en 1934). Esta condición dice que la circunferencia circunscrita de cada triángulo de la red no debe contener ningún vértice de otro triángulo. Se usan triangulaciones de Delaunay especialmente computación gráfica en tres dimensiones. Por su parte, el diagrama de Voronoi (denominado así por el también matemático ruso Georgy Voronoi, que en 1908 lo estudió) representa un esquema geométrico simple desde el que se define un método de interpolación sencillo, cuya descripción se presenta en la siguiente sección. Entre las aplicaciones de los diagramas de Voronoi se encuentran: la física de polímeros, la derivación de redes inalámbricas y la climatología (para una revisión más detalladas de los temas descritos en esta sección, revisar Berg et al., 2008.
Diagramas de Voronoi de segundo orden e interpolación por vecinos naturales
Existen, igualmente, diagramas de Voronoi de segundo orden, los cuales no son más que una extensión de los primeros:
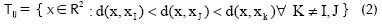
La anterior expresión define entonces una región TIJ asociada a dos nodos diferentes I y J, que se caracteriza porque cualquier punto x dentro de ella es más cercano a los nodos I y J que a cualquier otro nodo k de la nube de puntos estudiada. La celda TIJ corresponderá a una región vacía si los nodos I y J no son vecinos.
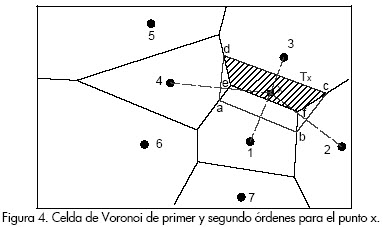
En la Figura 4 se muestra en líneas rojas la celda de Voronoi de segundo orden para un punto x que ha sido introducido en el diagrama de Voronoi de la Figura 3. Los vecinos naturales del punto x corresponden a los nodos que comparten uno de los lados de la celda de Voronoi (de segundo orden). En el ejemplo mostrado en la Figura 4, los nodos 1, 2, 3 y 4 son los vecinos naturales de x.
La coordenada natural del punto x de la Figura 4 respecto del nodo I, ΦI(x) se define mediante la siguiente relación:
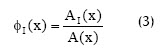
Donde A(x) es el área de la celda de Voronoi de primer orden asociada al punto x, y AI(x) el área de la celda de segundo orden asociada al punto x y el nodo I.
La definición de la coordenada de vecino natural de un nodo x respecto a un nodo I, basada en la definición de los diagramas de Voronoi, permite definir la interpolación por vecinos naturales, de la siguiente manera:
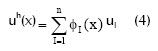
La cual permite calcular el valor aproximado de la variable de interés uh(x) en un punto 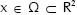 , a partir de los valores nodales de la variable, uI, y de las coordenadas naturales ΦI(x) (coordenada de vecino natural de x respecto al nodo nI), para cada uno de los n vecinos naturales del punto x. Comúnmente en métodos numéricos de ingeniería, las coordenadas ΦI(x) son denominadas las funciones de forma del método.
, a partir de los valores nodales de la variable, uI, y de las coordenadas naturales ΦI(x) (coordenada de vecino natural de x respecto al nodo nI), para cada uno de los n vecinos naturales del punto x. Comúnmente en métodos numéricos de ingeniería, las coordenadas ΦI(x) son denominadas las funciones de forma del método.
Características de la interpolación por vecinos naturales
Una ventaja importante de la interpolación por vecinos naturales sobre otros métodos sin malla es que es estrictamente interpolante, esto se refiere a que la superficie aproximada obtenida pasa por los valores nodales (Cueto, 2001; Cueto et al., 2003; González et al., 2003). Esto hace que en el MEN la imposición de las condiciones esenciales de frontera se puede hacer de forma directa, sin necesidad de usar estrategias adicionales para que la superficie de solución cumpla con estas condiciones de frontera, al menos en los nodos del contorno. Esto se debe a que la satisfacción de las condiciones en los nodos del contorno no la implica sobre todo el contorno, lo cual dependerá de las características del método de interpolación y de la naturaleza de las condiciones de contorno (Cueto, 2001).
Además, otras dos propiedades que garantizan la consistencia lineal de MEN son: las funciones de forma ΦI(x) constituyen una partición de la unidad de orden 0, o equivalentemente:
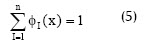
y la segunda:
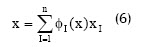
La consistencia lineal es la representación exacta de campos lineales (demostrable fácilmente desde estas dos propiedades), y es necesaria para la convergencia de la solución aproximada de ecuaciones diferenciales de segundo grado, tal como la ecuación de elasticidad (Sukumar, 1998).
Las funciones de forma del MEN ΦI(x) son diferentes de cero en una región contenida dentro del dominio geométrico definido por la nube de puntos, conocida como el soporte de la función. La naturaleza de la interpolación por vecinos naturales en su forma estándar genera funciones de forma âpuntudasâ dentro del soporte en los nodos a los que están asociadas; la Figura 5 muestra el soporte y la forma característica de una función ΦI(x), se puede apreciar que el soporte es la intersección de varias regiones circulares. Lo anterior sucede porque las funciones ΦI(x) son de clase Câ, sobre todo su soporte, exceptuando el nodo al que están asociadas, donde la continuidad es de tipo C0; esto implica que poseen discontinuidades desde la primera derivada en la frontera en el nodo al que está referida, y por tanto el MEN en su forma estándar no es adecuado para describir la primera derivada de la variable de interés en los nodos (salvo que se realice alguna modificación para calcular los valores nodales).
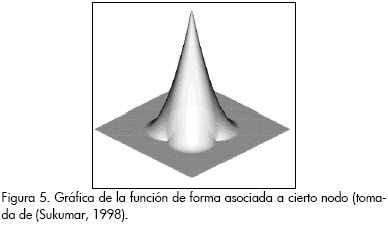
El MEN en una dimensión es idéntico al método de los elementos finitos lineal.
Vecinos naturales y comportamiento del MEN en la frontera
La cantidad de vecinos naturales de un punto depende directamente de su ubicación y de la densidad de nodos alrededor del mismo, factores que a su vez afectan la exactitud de la aproximación obtenida (localmente), que será mejor cuando la cantidad de vecinos naturales sea mayor (Cai y Zhu, 2005). A este respecto la interpolación por vecinos naturales posee la ventaja de no ser sensible a la distribución de los nodos, ni a la regularidad de la triangulación; no se ha encontrado dependencia entre la distribución o forma de los triángulos de Dellaunay y los resultados que se obtienen con el MEN (Cueto, 2001).
El comportamiento de las funciones de forma del MEN sobre la frontera esencial del dominio definido por el conjunto de puntos es diferente para dominios convexos y no convexos. En dominios convexos las funciones de forma son estrictamente lineales, en no convexos esta condición no se puede garantizar en todos los casos (Cai y Zhu, 2005).
Método de los elementos naturales basado en formas alfa (MEN-α)
Para solucionar los problemas de no linealidad que presenta el MEN en dominios no convexos y facilitar la delimitación del dominio geométrico a partir de una nube de puntos, se ha propuesto el MEN-α (Cueto, 2001), que introduce un cambio en la definición del diagrama de las celdas de Voronoi y logra de esta manera la linealidad de las funciones de forma en cualquier tipo de dominio4.
Una forma α se usa para extraer información acerca de la âformaâ asociada a una nube de puntos, ya sea en dos o tres dimensiones, siendo muy usada en el campo de la visualización científica (Berg et al., 2008). Conceptualmente hablando, las formas α son una generalización de la envoltura convexa (CH)5 de un conjunto de puntos S. El nivel de detalle logrado, que no puede ser menor que la mínima distancia entre puntos, es dado por un parámetro real dentro del intervalo [0,â), denotado por α (Sukuma, 1998). Sin entrar en mayores detalles, se puede resumir el inconveniente de la no linealidad que presenta el MEN estándar en las fronteras no convexas en dominios bidimensionales, como sigue; por la definición de celda de Voronoi presentada en la ecuación. (1) un punto en una frontera no convexa puede verse influenciado por más de dos nodos, lo que causa el comportamiento no lineal de la variable aproximada en la frontera esencial. La estrategia que usa el MEN-α es cambiar la definición de celda de Voronoi de manera que un punto de la frontera no incluya dentro de su frontera más que nodos pertenecientes a la frontera (Cueto, 2001). La definición formal de una celda de Voronoi en el MEN-α es la siguiente:
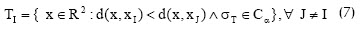
Los términos adicionales en esta expresión, comparándola con (1), se incluyen para garantizar la linealidad de las funciones de forma en el contorno6. En la figura de abajo se muestra el ejemplo del uso de formas alfa para determinar la forma de una nube de puntos en el espacio.
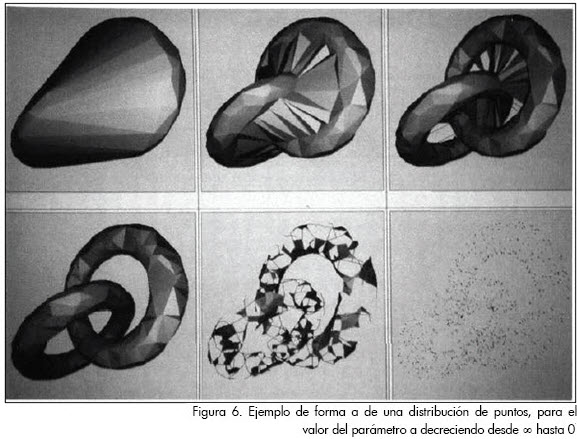 7
7En este trabajo se usaron formas alfa descritas para extraer las formas asociadas a las nubes de puntos de los problemas tipo estudiados, aunque como se trata de geometrías simples su uso se habría podido evitar.
Solución de algunos problemas estructurales
Se realizó el estudio de dos problemas de elasticidad lineal bidimensionales con geometrías y condiciones de carga sencillas, usando un código escrito en Matlab 6.5 (González, 2004). Se compararon las soluciones aproximadas con el método de los elementos naturales, el método de los elementos finitos (con elementos triangulares lineales y cuadriláteros bilineales) y la solución analítica exacta (Mal y Singh, 1991).
En esta sección se presenta la descripción del proceso de solución numérica de un problema estructural usando el MEN, los casos estudiados y los resultados obtenidos.
Obtención de la forma débil
Las ecuaciones que gobiernan el comportamiento elástico-estático en pequeñas deformaciones de cuerpos como el de la Figura 7 (Ovivella y De Saracíbar, 2002), escritas en su forma tensorial, son:
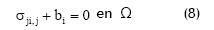

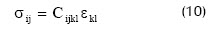
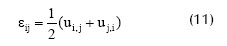
En estas ecuaciones σij es el tensor de esfuerzos de Cauchy, εij es el tensor de pequeñas deformaciones, bij es el vector que contiene las fuerzas de cuerpo por unidad de volumen en cada dirección i, Cijkl es el tensor de constantes elásticas y ui es el vector de desplazamientos. Cada elemento del tensor σij o εij corresponde al esfuerzo o deformación en dirección xj sobre la cara de un elemento diferencial, cuyo vector normal tiene la dirección del eje xi.
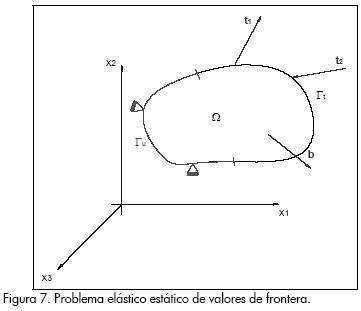
Las condiciones de frontera del cuerpo de la Figura 4 están dadas por:
Siendo Γu y Γt la frontera esencial y natural, respectivamente.
A partir de la multiplicación de la ecuación (8) por una función de prueba8 (o ponderación) vi y la posterior integración sobre el dominio Ω, se obtiene:
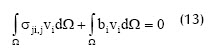
Al aplicar el teorema de Green a la primera integral de la ecuación, asumir vi igual a cero en la frontera esencial, y reordenar la expresión, se obtiene:
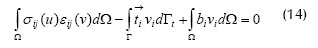
La obtención de una forma discreta de la ecuación (14) que pueda ser resuelta numéricamente se consigue mediante la implementación del método de Bubnov-Galerkin, inicialmente aproximando las funciones desde sus valores nodales, usando la interpolación por vecinos naturales descrita anteriormente:
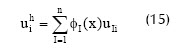
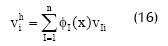
Y al reemplazarlas en la ecuación (14) la transforman en:
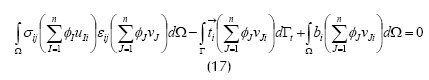
Por las propiedades de linealidad se puede escribir como:
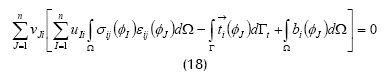
Como las funciones v son arbitrarias, la expresión anterior es equivalente a:
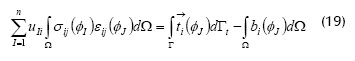
Que se puede escribir como:
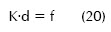
Donde K es la llamada matriz de rigidez, d el vector de desplazamientos y f el vector de fuerza externa. La matriz de rigidez y el vector de fuerza externa se pueden calcular a nivel local (para cada pareja de nodos I y J) y después realizar un ensamble para calcular tanto la matriz como el vector globales. La matriz y el vector locales se pueden definir desde (19) como:
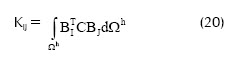
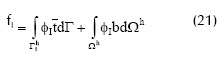
donde:
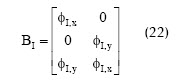
Con lo anterior, el problema de encontrar el campo de desplazamientos de un sólido que se deforma elásticamente se reduce a la solución de un sistema de ecuaciones lineales de tipo sparse, es decir, en los que la matriz de rigidez y el vector de fuerza externa contienen gran cantidad de elementos nulos. Existen varios métodos para la solución de estos sistemas óptimamente, siendo el método de Gradiente Biconjugado (BICG) uno de los más utilizados (Saad, 2000). En el caso de problemas con una cantidad de nodos âpequeñaâ, tales como los dos que se presentan en seguida, se pueden usar los métodos tradicionales, o métodos para matrices dense (donde la cantidad de elementos nulos es mínima).
Problemas resueltos
En los problemas que siguen se tomaron como propiedades del material un módulo de elasticidad E = 2 x 107 N/cm2 y un coeficiente de Poisson ν=0.25, las integrales fueron calculadas usando el método de cuadratura de Gauss-Legendre de 3 puntos en la integración de la forma débil y de 25 puntos para el cálculo de las normas de error. En el caso de los elementos finitos para elementos cuadriláteros se usó una cuadratura de 9 puntos para la integración de la forma débil y de 16 puntos para las normas de error. En todos los problemas las geometrías fueron definidas a partir de nubes de puntos usando formas α.
Placa con agujero circular
Se presenta inicialmente el problema de una placa con un agujero, como la que se muestra en la Figura 8.

Para este y los demás problemas presentados se usaron distintas discretizaciones y se compararon los resultados conseguidos con el MEN, el MEF y la solución analítica, igualmente se calcularon las normas de error de desplazamiento y energético de las ecuaciones (24) y (25), respectivamente. En el caso de la placa se usaron grillas de 42, 141, 513 y 1.953 nodos; en la Figura 9 se observa que la densidad de nodos varía, siendo mayor cerca del agujero, donde se presentan los mayores gradientes de la variable desplazamiento.
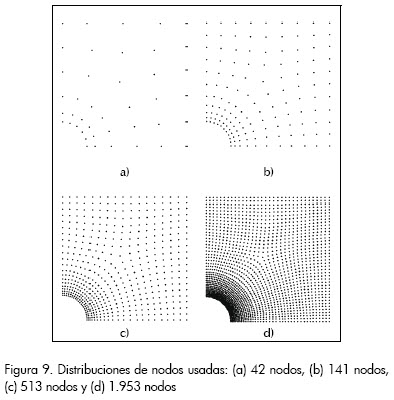
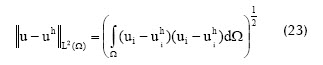
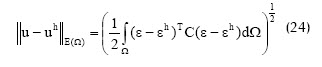
donde u es el campo de desplazamientos analítico y uh el aproximado, análogamente las deformaciones ε y εh.
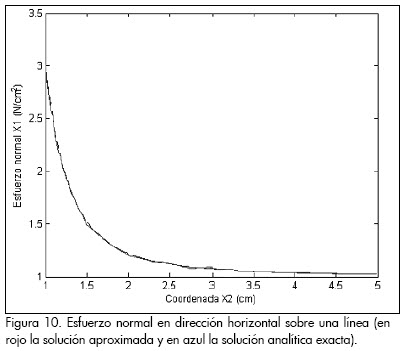
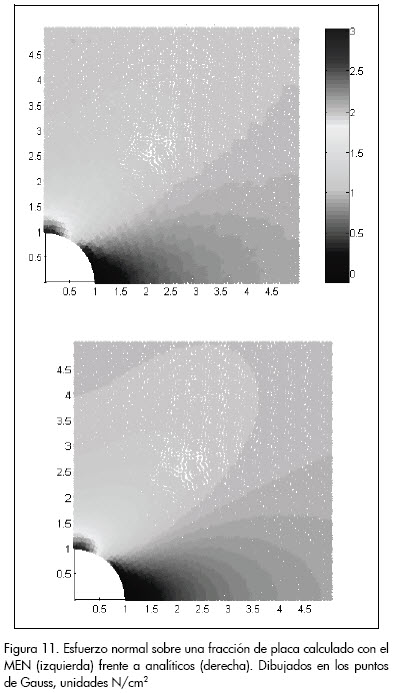
Por la simetría de la geometría y de las cargas aplicadas tanto para un eje vertical como uno horizontal que pasan por el centro del agujero (Figura 8), los cálculos se realizaron únicamente para un cuarto de placa. La Figura 10 muestra el esfuerzo normal en dirección horizontal obtenido por el MEN (línea roja) y analíticamente (línea azul) sobre una línea vertical que va desde el punto más bajo del agujero, donde se presenta el mayor esfuerzo, hasta el extremo inferior de la placa sobre, donde el esfuerzo normal es mínimo, se observa la proximidad entre las dos curvas, al igual que en la Figura 11, donde se presenta la distribución de esfuerzos normales en dirección horizontal sobre una fracción de placa.
El error relativo de desplazamiento fue mayor usando el MEF con elementos triangulares (MEF-tri), seguido por el calculado con elementos cuadriláteros (MEF-cuad) y el MEN, para el que se consiguieron los mínimos errores (ver Tabla 1).

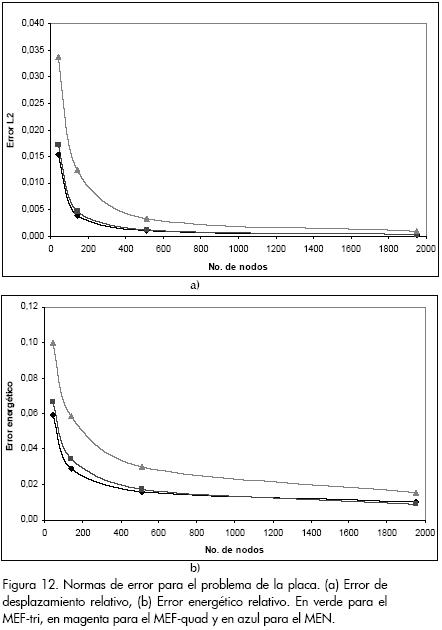
Las normas de desplazamiento y energéticas definidas al principio de la sección permiten comparar la exactitud de los métodos numéricos usados. Las Figura 12 (a) y (b) muestran las normas de error de desplazamiento y energético para las grillas usadas, la línea con triángulos (verde) corresponde a las curvas de error calculado para el MEF-tri, con cuadrados (magenta) para el MEF-cuad, y con rombos (azul) para el MEN. Los mayores valores de las normas de error se obtienen para el MEF-tri y los menores para el MEN.
Viga empotrada
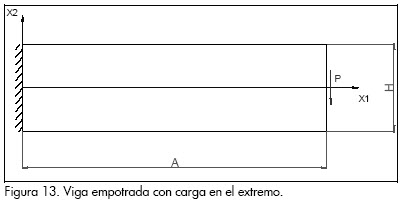
La segunda situación que se estudió fue una viga empotrada, con una carga en su extremo (Figura 13).
En este caso se usaron grillas regulares de 85, 297, 1.105, 1.701 y 2.626 nodos como las de la Figura 14.
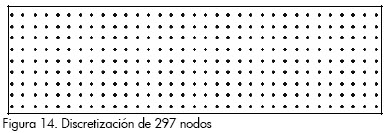
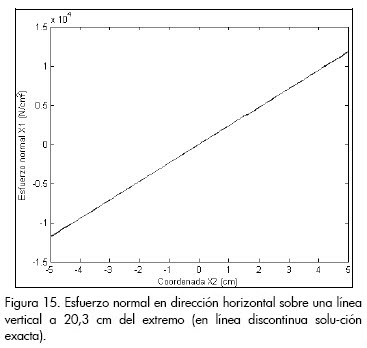
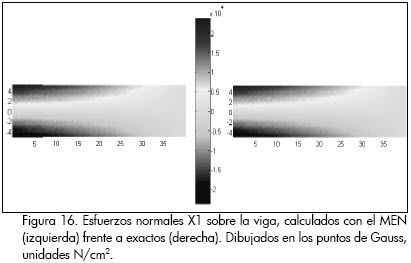
De nuevo se observó proximidad entre la solución obtenida con el MEN y la analítica, en ambos casos: tanto sobre una línea vertical de la sección transversal de la viga cerca da la zona de empotramiento (fig. 15), como en el estado de esfuerzos normales en dirección horizontal sobre todo el dominio (Figura 16).
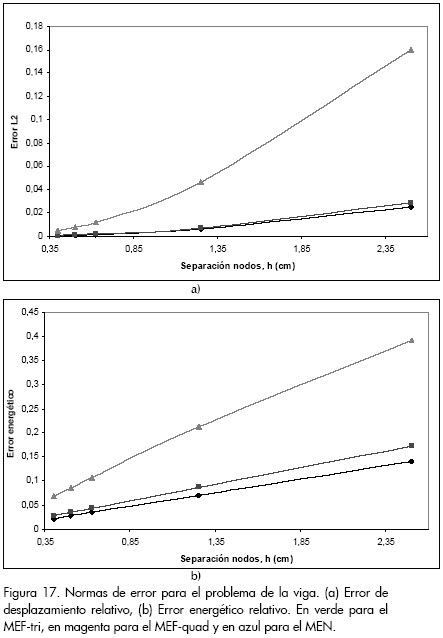
La Figura 17 muestra las normas de error para distintos valores de distancia máxima entre nodos (h). Se observó que las normas de error fueron significativamente mayores en el caso del MEF-tri, y muy semejantes para el MEF-cuad y el MEN, siendo siempre menores para el MEN.
Conclusiones
Se ha realizado una revisión del método de los elementos naturales, en el que la conectividad entre los elementos es determinada automáticamente por medio de un algoritmo propio de triangulación. Esto constituye una ventaja importante sobre los métodos tradicionales ya que el usuario no debe verse involucrado en el proceso de mallado.
El hecho de que el MEF, el MEN y otras técnicas sin malla estén basadas en el método de Galerkin hace que la implementación computacional sea similar, lo que posibilita el uso de las estructuras usadas por un código de elementos finitos en aplicaciones que implementen otro método, y facilita el acoplamiento MEF-método sin malla, tal y como se ha hecho en algunos trabajos (Deeks y Augarde, 2007; Chew et al., 2006; Arantes y Oliveira, 2005).
En problemas estáticos de elasticidad lineal bajo pequeñas deformaciones, la solución aproximada con el MEN estándar mostró estar de acuerdo con la solución analítica exacta, y presentó un comportamiento en cuanto a convergencia y exactitud, comparable y en la mayoría de casos superior a las obtenidas con el MEF usando elementos cuadriláteros bilineales y en todos los casos superior al MEF con elementos triangulares lineales. En la Figura 12 (b) se observa que para la grilla con un número de nodos mayor (1.941) se obtuvo una mejor aproximación usando el MEF-cuad que la obtenida por el MEN, esto se puede deber a que con mallas de un gran número de nodos los errores de integración se vuelven más representativos en el MEN, debido a que se usó la cuadratura de Gauss-Legendre, propuesta para aproximar integrales en regiones simples (triángulos, cuadriláteros) y no para las formas de los soportes de las funciones de forma del MEN, que como se dijo, son intersecciones de regiones circulares.
Una desventaja del MEN que se hizo evidente en las simulaciones realizadas es la discontinuidad de las derivadas de las funciones de forma en los nodos, lo cual se manifiesta en elevados valores de los esfuerzos cerca de estos puntos, este inconveniente también se presenta en algunos planteamientos del método de los elementos finitos calculando los esfuerzos en los puntos de Gauss y luego calculando mediante algún método interpolación los valores de los esfuerzos en los nodos (Oñate et al .,2004).
Aunque el tiempo de cálculo no fue medido, en las simulaciones realizadas se pudo apreciar un mayor tiempo de cómputo requerido por el método de los elementos naturales, comparado con el de los elementos finitos. Esto se debe a la necesidad de cálculo de los vecinos naturales y de las funciones de forma del MEN, que es más compleja que el MEF. En la literatura se reporta que el MEN estándar puede requerir tiempos de cómputo de una a dos veces mayores que el método de los elementos finitos (Sukumar, 1998) en dos dimensiones, con diferencias mayores en casos tridimensionales.
La introducción de puntos adicionales en cualquier zona del dominio no es causa de inexactitudes o inconformidades en el MEN, ya que el nivel de aproximación conseguido depende más de la densidad que de la regularidad de la distribución de los nodos. Esto puede facilitar la ejecución de una estrategia de solución adaptable, en la que en zonas con gradientes elevados de la variable incógnita se adicionen nuevos puntos para disminuir el error de aproximación resultante y de esta manera conseguir una solución que acerque más a los valores exactos de las variables de interés en estas zonas.
Lo anterior muestra la aplicabilidad del método, al menos en problemas del tipo estudiado, es decir, con condiciones de carga y geometrías âsencillasâ. En Alfaro et al., 2006 se muestra la aplicación del método a problemas más complejos.
El método de los elementos naturales se muestra apropiado para la solución de sistemas de ecuaciones diferenciales en biomecánica, en mecánica de sólidos con grandes deformaciones y en mecánica de fluidos, de hecho en estos y otros tipos de problemas de cierto grado de complejidad el método ha sido usado con resultados satisfactorios (ver, p. e., Alfaro et al., 2006). En el caso de aplicaciones biomédicas el método puede ser especialmente útil, pues en general la descripción del dominio que representa cierto tejido vivo se obtiene de técnicas digitales como la tomografía axial computarizada (TAC) para huesos y la resonancia magnética (MRI) para tejidos blandos, las cuales al ser procesadas definen la geometría de los tejidos a través de una nube de puntos.
Para avanzar en la comprensión y el conocimiento del método de elementos naturales y de otros métodos sin malla, se plantea la implementación del MEN para dominios tridimensionales, la búsqueda de algoritmos óptimos para el mallado automático a partir de una nube de puntos en el espacio, la implementación de métodos híbridos que aprovechen las ventajas de los sin malla y de otros métodos numéricos como el MEF. Igualmente, se podrían abordar temas como la búsqueda de métodos de integración apropiados para integrar sobre los soportes de las funciones de forma del MEN.
4 Aunque no para todos los casos en dominios no convexos.
5 La envoltura convexa, CH(S), se puede entender intuitivamente como el mínimo conjunto que encierra todos los puntos de S.
6 Una revisión más profunda de las formas alfa se puede hallar en libros de geometría computacional como (Berg et al., 2008).
7 Fuente: http://www.lems.brown.edu/vision/people/leymarie/Refs/CompGeom/Edelsbrunner.html.
8 vi pertenece a un espacio de Sobolev (Cueto, 2001), y presenta características especiales en Ît (Sukumar, 1998).
Bibliografía
Alfaro, I., Bel, D., Cueto, E., Doblare, M., Chinesta, F., Three-dimensional simulation of aluminium extrusion by the [alpha]-shape based natural element method., Computer Methods in Applied Mechanics and Engineering. Vol. 195, No. 33-36, 1 July 2006, pp. 4269-4286. [ Links ]
Berg, M., Cheong, O., Van Kreveld, M., Overmars, M., Computational Geometry: Algorithms and Applications., 3rd ed, Springer, 2008. [ Links ]
Cai, Y., Zhu, H., A local search algorithm for natural neigh-bours in the natural element method, International Journal of Solids and Structures, Vol. 42, No. 23, 2005, pp. 6059-6070. [ Links ]
Chew, C.S., Yeo K.S., Shu, C., A generalized finite-difference (GFD) ALE scheme for incompressible flows around moving solid bodies on hybrid meshfree-Cartesian grids., Journal of Computational Physics, Vol. 218, No. 2, 1 November 2006, pp. 510-548. [ Links ]
Cueto, E., El Método de los Elementos Naturales basado en formas-α (MEN-α): Aplicación a la simulación de la remodelación interna de fracturas de cadera con sistema Ãxeter)., Tesis presentada a la Universidad de Zaragoza, Zaragoza para optar al titulo de Doctor, 2001. [ Links ]
Cueto, E., Sukumar, N., Calvo, B., Cegoñino, J., Doblaré, M., Overview and Recent Advances in Natural Neighbour Galerkin Methods., Archives of Computational Methods in Engineering, Vol. 10, No. 4, 2003. pp. 307-384. [ Links ]
De Arantes e Oliveira, E. R., From formal solutions to computational methods avoiding passages to the limit., Engineering Analysis with Boundary Elements, Vol. 29, No. 4, Mesh Reduction Methods - Part III, 2005, pp. 305-312. [ Links ]
Deeks, A. J., Augarde, Ch. E., A hybrid meshless local Petrov-Galerkin method for unbounded domains, Computer Methods in Applied Mechanics and Engineering, Vol. 196, No. 4-6, 1 January 2007, pp. 843-852. [ Links ]
Del Coz Diaz, J. J., Garcia Nieto, P. J., Vilan Vilan, J. A., Rodriguez, A. M., Prado Tamargo, J. R., Lozano Martinez-Luengas, A., Non-linear analysis and warping of tubular pipe conveyors by the finite element method, Mathematical and Computer Modelling, Vol. 46, No. 1-2, Proceedings of the International Conference on Computational Methods in Sciences and Engineering, 2004, July 2007, pp. 95-108. [ Links ]
Doblare, M., Cueto, E., Calvo, B., Martinez, M. A., Garcia, J. M., Cegonino, J., On the employ of meshless methods in biomechanics, Computer Methods in Applied Mechanics and Engineering, Vol. 194, No. 6-8, 2005, pp. 801-821. [ Links ]
Dunn, S. M., Constantinides, A., Moghe, P. V., Finite Difference Methods, Interpolation and Integration., Numerical Methods in Biomedical Engineering, Academic Press, Burlington, 2006, pp. 163-208. [ Links ]
Cho, J. R., Lee, H. W., 2-D frictionless dynamic contact analysis of large deformable bodies by Petrov-Galerkin natural element method., Computers & Structures, Vol. 85, No. 15-16, August 2007, pp. 1230-1242. [ Links ]
González, D., Cueto, E., Martínez, M. A., Doblaré, M., Integración numérica en métodos de Galerkin de Vecindad natural., Actas del Congreso Español de Ecuaciones diferenciales y Aplicaciones (CEDYA 2003), Tarragona (España), 2003. [ Links ]
González, L. A., Aplicación del método de los elementos naturales a problemas estructurales., Tesis de pregrado. Universidad Nacional de Colombia, 2004. [ Links ]
Griffiths, D. V., Numerical methods for engineers: a programming approach., Editor Boca Ratón, Florida, 1991. [ Links ]
Hajri I., Omri, A., Ben Nasrallah, S., A numerical model for the simulation of double-diffusive natural convection in a traingular cavity using equal order and control volume based on the finite element method., Desalination, Vol. 206, No. 1-3, 2007, pp. 579-588. [ Links ]
Kwon, Y. W., Bang, H., The finite element method using matlab., second edition, Editor Frank Kreith, 2000. [ Links ]
Lademo, O.G., Berstad, T., Eriksson, M., Tryland, T., Furu, T., Hopperstad O. S., Langseth, M., A model for process-based crash simulation., International Journal of Impact Engineering, Vol. 35, No. 5, May 2008, pp. 376-388. [ Links ]
Mal, A. K., Singh, S. J., Deformation of elastic solids., Prentice Hall, New Jersey,1991. [ Links ]
Olivella, X O., De Saracíbar, C. B., Mecánica de medios continuos para ingenieros, Alfaomega, México, 2002. [ Links ]
Ollivier-Gooch, C., A toolkit for numerical simulation of PDEs: I. Fundamentals of generic finite-volume simulation., Computer Methods in Applied Mechanics and Engineering. Vol.192, No. 9-10, 28, 2003, pp. 1147-1175. [ Links ]
Oñate, E., Rojek, J., Taylor, R. L., Zienkiewicz, O. C., Finite calculus formulation for incompressible solids using linear triangles and tetrahedral., Int. J. Numer. Methods Eng. 59, 2004, pp. 1473â1500. [ Links ]
Pena, E., Martinez, M. A., Calvo, B., Doblare, M., Application of the natural element method to finite deformation inelastic problems in isotropic and fiber-reinforced biological soft tissues, Computer Methods in Applied Mechanics and EngineeringIn Press, Corrected Proof, Available online 15 January 2008. [ Links ]
Prabhakar, V., Reddy, J. N., Spectral/hp penalty least-squares finite element formulation for the steady incompressible Navier-Stokes equations., Journal of Computational Physics. Vol. 215, No. 1, 10 June 2006, pp. 274-297. [ Links ]
Saad, Y., Iterative Methods for sparse linear systems., 2ed, 2000. [ Links ]
Sukumar, N., The Natural Element Method in Solid Mechanics., Tesis presentada a la Northwestern University, Evaston, Illinois, Para optar por el título de Ph.D, 1998. [ Links ]
Timoshenko, S., Goodier J., Teoría de Elasticidad, Editorial urmo, 1972. [ Links ]














