Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.28 no.1 Bogotá Jan./Apr. 2008
Mónica Jimena Ortiz Jerez1, Carlos Antonio Vélez Pasos2 y Edinson Franco Mejía3
1 Ingeniera química. Candidata M.Sc. Estudiante, Doctorado, Ingeniería de Alimentos, Universidad del Valle. Colombia. mortirez@univalle.edu.co
2 Ph.D., Ingeniería de Alimentos. Profesor titular, Universidad del Valle. Colombia. cvelez@univalle.edu.co
3 Ph.D. Ingeniería Eléctrica. Profesor titular, Universidad del Valle, Colombia. edinsonfm@univalle.edu.co
RESUMEN
La mayor dificultad durante la microfiltración tangencial es la formación de una capa de torta en la superficie membranaria, también llamada colmatación, la cual afecta el desempeño del sistema. La colmatación se ha relacionado al decaimiento del flux de permeado como resultado de cambios en las variables de operación. Muchos trabajos se han publicado para explicar este fenómeno, pero aún no se ha entendido totalmente porque depende de interacciones específicas solución/membrana y de diversos parámetros. El objeto de este trabajo es presentar una revisión analítica de los modelos matemáticos recientemente publicados para explicar el fenómeno de colmatación. Aunque los modelos revisados se ajustan a cualquier tipo de aplicación, en el caso particular de jugos de frutas tropicales, un modelo sencillo de polarización de la concentración es conveniente para describir la deposición de los sólidos insolubles en la superficie de la membrana.
Palabras clave: colmatación, membranas, microfiltración, modelos matemáticos, polarización de la concentración, bloqueo de poro, difusión de corte inducido, migración lateral.
ABSTRACT
The greatest difficulty arising during cross-flow micro-filtration is the formation of a cake layer on the membrane surface (also called fouling), thereby affecting system performance. Fouling has been related to permeate flux decay resulting from changes in operating variables. Many articles have been published in an attempt to explain this phenomenon but it has not yet been fully understood because it depends on specific solution/membrane interactions and differing parameters. This work was aimed at presenting an analytical review of recently published mathematical models to explain fouling. Although the reviewed models can be adjusted to any type of application, a simple concentration polarisation model is advisable in the particular case of tropical fruit juices for describing the insoluble solids being deposited on membrane surface.
Keywords: fouling, membrane, microfiltration, mathematical model, concentration polarisation, pore blocking, shear-induced diffusion, lateral migration.
Recibido: noviembre 26 de 2007
Aceptado: febrero 21 de 2008
Introducción
La microfiltración tangencial (MFT) es un proceso que utiliza membranas semipermeables para la concentración, purificación o separación de partículas finas, microorganismos y gotas de emulsión en procesos biotecnológicos, en la industria de alimentos y en el tratamiento de aguas residuales, entre otros. La separación es debida a la presión, fuerza motriz del proceso. Tangencialmente a la superficie de filtración fluye un retenido constituido por sustancias que no pueden atravesar los poros de la membrana, y paralelo a ella, hay un flujo de permeado que en la mayoría de los casos tiene un alto valor comercial, constituido por partículas que pueden pasar la membrana (Vaillant et al., 2004). Las membranas usadas en estos procesos tienen una estructura microporosa, fabricadas en diferentes materiales y que por su tamaño de poro separan partículas con tamaños entre 0,02 – 20 μm. Este proceso de separación tiene ciertas ventajas con respecto a otros: es atérmico, no involucra cambios de fase, requiere baja presión hidrostática, se realiza a baja temperatura. Por eso es muy usado para producir líquidos puros, para concentrar suspensiones, recuperar productos de gran valor y para regenerar líquidos de proceso (Vyas et al., 2002).
El proceso de MFT está limitado principalmente por la formación de una torta en la superficie de la membrana y por la colmatación interna de la membrana. El entendimiento de estos fenómenos resultaría en un uso más económico ya que la progresiva formación de esta capa afecta negativamente las condiciones de la operación, haciendo difícil el control del proceso e incrementando paradas de planta para limpieza de las membranas. Cuando se procesan jugos de fruta ricos en pulpa los polisacáridos presentes en las paredes celulares, como pectina, celulosa, lignina y hemicelulosa, son responsables de la capa de colmataje. En tales casos se hidrolizan los polisacáridos mediante enzimas para mejorar el filtrado. A pesar de ello se presentan dificultades en la operación y disminución en el rendimiento del equipo (Vélez et al., 2007).
Algunos autores han relacionado el decaimiento del flux de permeado con la colmatación como resultado del incremento de las resistencias al flujo; condiciones de operación; productos a tratar; tipo de membrana y fenómenos de transporte (Choi et al.,2005; Jiraratananon y Chanachai, 1996; Ye et al., 2005; Youn et al., 2004; Balakrishnan et al., 2000; Cumming et al., 1999; Thomassen et al., 2005; Vaillant et al., 2001; Vyas et al., 2002; Wang y Song, 1999; Vaillant et al., 2005; Vaillant et al., 1999; Hwang y Lin, 2002; Jonsson et al., 1996; Riedl et al., 1998; Curcio et al., 2005; Curcio et al., 2001; Nassehi, 1998; Wiley y Fletcher, 2003). Estos estudios han contribuido al avance en la modelación del fenómeno sin que exista un modelo global que incluya todos los aspectos anteriores. El objeto de este trabajo es presentar una revisión analítica de los modelos matemáticos recientemente publicados para explicar el fenómeno de colmatación durante la MFT que permita seleccionar un modelo adecuado cuando se tratan jugos de frutas tropicales.
Teoría de la colmatación
El comportamiento de una membrana puede cambiar en los procesos de filtración tangencial al presentarse disminución del flux de permeado debido a la acumulación de partículas en la superficie de la membrana. Este fenómeno, llamado colmatación, es causado por diferentes mecanismos, tales como: polarización de la concentración (PC) (Jiraratananon y Chanachai, 1996; Jonsson et al., 1996; Riedl et al., 1998; Song, 1998b), bloqueo del poro (Hermia, 1982; Kawakatsu et al., 1995), incremento de la viscosidad por aumento del factor de concentración (Carneiro et al., 2002).
La microfiltración está basada en la teoría de la filtración tradicional descrita por la ley de Darcy (Bird, Stewart y Lightfoot, 1993), en la cual el flux de permeado es función de la presión transmembranaria y de una resistencia total:

donde J: flux de permeado (m/s); PTM: presión transmembranaria (Pa); μ: viscosidad del producto (Pa.s), y Rt: resistencia total (m-1). Según esta teoría, las condiciones de operación que influyen en el flux de permeado son: i) presión transmembranaria (PTM) dada por la diferencia de presiones a ambos lados de la membrana. La influencia de esta variable sobre el flujo es imprevisible y depende de las características del soluto a tratar; ii) velocidad tangencial, promedio de la velocidad axial del fluido. A mayor velocidad tangencial, mayor flujo, pero está limitada por el tamaño de las bombas y el costo energético. De este factor depende el fenómeno de erosión de la pared de la membrana para mantener limpia la superficie; también permite que el flujo sea turbulento, iii) temperatura, a mayor temperatura menor será la viscosidad del producto y mayor la difusión, esto incrementará el flux, pero una temperatura alta puede afectar la calidad final del producto. De la Ecuación (1), el término Rt puede definirse como:
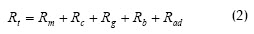
donde Rm: resistencia de la membrana limpia o nueva; Rc: resistencia de la capa de torta; Rg: resistencia del gel; Rb: resistencia debida al bloqueo de poro, y Rad: resistencia por adsorción.
Idealmente, en el proceso sólo estaría involucrada la resistencia intrínseca de la membrana, Rm,, dada por la forma y tamaño de los poros y el espesor de la membrana (Choi et al.,2005) capaz de transportar unos compuestos más fácilmente que otros, provocando una acumulación de moléculas cerca de la superficie de la membrana y generando una resistencia a la transferencia de masa, llamada polarización de la concentración; Rc , dada por el contrabalance de las moles de soluto que tienden a pasar a través de la membrana y aquellas que se difunden hacia el seno del líquido. Puede ser considerada como una colmatación reversible porque sus efectos pueden reducirse disminuyendo la presión transmembranaria o alimentando al sistema una solución de menor concentración (Curcio et al., 2001; Jonsson et al., 1996; Ripperger y Altmann, 2002).
Cuando la concentración de moléculas de soluto acumulado es muy alta se forma una capa de partículas sobre la membrana llamada capa de gel, generando una resistencia Rg. En membranas porosas es posible que algunas partículas del mismo tamaño de poro penetren la membrana y se depositen sobre la superficie para formar una torta filtrante o un bloque en los poros de la membrana, denominada resistencia de poro bloqueado, Rb. La deposición de solutos en los poros o en la superficie membranaria (adsorción) genera una resistencia adicional Rad. Este fenómeno es termodinámicamente inevitable e irreversible, pero su contribución a la resistencia total de filtración es muy pequeña (Choi et al., 2005).
Por el momento no hay publicado un modelo de colmatación que incluya la totalidad de las variables que afectan el proceso; sin embargo, los intentos de modelación, incluyendo algunos parámetros, han ido ganando buena aceptación. Varios de ellos se analizan en la siguiente sección.
Modelos matemáticos
Ripperger y Altmann (2002) clasifican los modelos de microfiltración en empíricos y físicos. Los primeros son útiles en la práctica pero no para el entendimiento del proceso, y por eso en este trabajo no se discuten. Los segundos están regidos por mecanismos físicos y se clasifican a su vez en modelos macroscópicos y microscópicos. Los macroscópicos consideran las partículas como un sistema continuo, mientras que los microscópicos consideran el comportamiento de una partícula individual como sistema. Ambas aproximaciones reducen el gran número de parámetros influyentes y se desarrollan siguiendo los lineamientos de alguno de los siguientes tres mecanismos físicos básicos: hidrodinámica de partículas; difusión de partículas, e interacción de partículas y efectos de superficie.
Los modelos presentados a continuación son meramente físicos y han sido validados por sus respectivos autores para diversas aplicaciones. Según el mecanismo de colmatación se pueden organizar bajo las siguientes categorías: a) Modelos de resistencias en serie, b) Modelos de bloqueo de poro y formación de la torta, c) Modelos de polarización de la concentración, d) Modelos de difusión hidrodinámica de corte inducido, e) Modelos de elevación inercial, y f) Modelos de transporte superficial
Modelo de resistencias en serie
Este modelo macroscópico se basa en la teoría de filtración descrita por la ley de Darcy (Ecuación 1). La principal modificación de la ley de Darcy fue hecha por Brinkman (1947) (Bird, Stewart y Lightfoot, 1993) quien incluyó un término adicional para cuantificar la distorsión de los perfiles de velocidad en las proximidades de las paredes (Balakrishnan et al., 2000; Curcio et al., 2005). Uno de los aportes experimentales más importantes a esta teoría fue el de Jiraratananon y Chanachai (1996) al basar su análisis en la reversibilidad e irreversibilidad del fenómeno. La resistencia reversible está conformada por Rc y por una película de gel como resultado de la máxima solubilidad de macromoléculas del jugo de fruta analizado. La resistencia irreversible consta de una resistencia semirreversible de la capa polarizada y una resistencia a la colmatación, o capa adsorbida que no se puede remover por limpieza con agua. Otros trabajos similares se han publicado (Carrère et al., 2002; Choi et al., 2005; Wang et al., 2005; Ye et al., 2005; You y Lencki, 2004). En todos los casos se usaron materiales biológicos, generalmente con aplicación en la industria de alimentos. La resistencia a la colmatación es función directa del espesor de la capa de torta y de la resistencia específica de la torta, esta última se puede calcular usando alguna forma de la ecuación de Carman-Kozeny (Altmann y Ripperger, 1997; Kawakatsu et al., 1995; Lee y Clark, 1998; Song, 1998b, Green y Belfort, 1980):
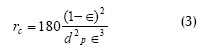
Donde rc es la resistencia específica de la torta; dp: diámetro de partícula, y ε: la porosidad de la torta. La Ecuación (3) es ampliamente usada para analizar la colmatación de la membrana siempre que los demás parámetros se obtengan experimental o analíticamente.
Bird y Barttlet (2002) usaron un modelo de resistencias en el procesamiento de concentrado de proteína de lactosuero usando microfiltración; el modelo describe la recuperación del flux de permeado en términos de la variación de dos resistencias hidráulicas durante la limpieza cáustica de una membrana de acero inoxidable; la resistencia debida a la colmatación interna del poro se representa mediante versión modificada de la ecuación de Carman-Kozeny (Ecuación (3)) y la resistencia de la torta es modelada como una resistencia de segundo orden que decrece en cuanto la torta se va retirando de la membrana. El modelo se ajusta acertadamente a los datos experimentales y deja abiertas las posibilidades de estudio con este enfoque porque es posible ver la variabilidad de otros parámetros en el tiempo. También es aplicable a membranas cerámicas.
Modelos de bloqueo del poro
Los investigadores de este mecanismo de colmatación coinciden en que Hermans y Bredée (1936), en sus tesis doctorales, formularon las cuatro leyes de bloqueo aplicables a fluidos no newtonianos que siguen la ley de potencia: bloqueo completo, bloqueo intermedio, bloqueo estándar, y torta filtrante. En el bloqueo completo el tamaño de partículas es mayor que el del poro de la membrana; las partículas se depositan sobre la superficie de la membrana bloqueando las entradas en los poros completamente. En el bloqueo intermedio el diámetro de las partículas es similar al de los poros; las partículas pueden depositarse en el poro o migrar hacia su interior. El bloqueo depende de la concentración de partículas (Hwang y Lin, 2002). En el bloqueo estándar el tamaño de las partículas es menor que el de los poros; unas pocas partículas se depositan sobre la superficie de la membrana mientras que otras son arrastradas por el filtrado atravesando los poros de la membrana y dan lugar a la colmatación en los poros. Finalmente, la formación de torta filtrante es similar al bloqueo completo; cuando la concentración de la suspensión es alta, las partículas se pueden depositar sobre la superficie de la membrana o sobre la capa de partículas depositadas para formar una torta de filtración. Para calcular el flux de permeado en cualquiera de los casos anteriores se emplea la ecuación dependiente del tiempo derivada por Hermia (1982):
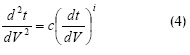
donde V volumen de filtrado por unidad de área de filtración; t: tiempo de filtración, el índice i y la constante c dependen del modelo de bloqueo. Para los modelos mencionados arriba i = 2 representa bloqueo completo, i = 1.5 bloqueo estándar, i = 1 bloqueo intermedio, mientras que i = 0 torta filtrante.
Kawakatsu et al. (1995) usaron las reglas del bloqueo de poro para entender el empaquetamiento aleatorio de partículas asumiendo una estructura 3D (romboedro tetragonal) con probabilidad de movimiento y estabilidad de las esferas. Basados en estas leyes, Jonsson et al. (1996) derivaron un modelo dinámico para describir el desempeño de diferentes tipos de membranas polisulfónicas de microfiltración bajo diversos parámetros de operación usando soluciones de BSA (suero albuminoso de bovino). Hwang y Lin (2002) también usaron estas leyes para estudiar el efecto de la morfología de diversas membranas (MF-Millipore, Durapore e Isopore) usadas en la microfiltración tangencial de suspensiones de partículas esféricas de polimetil metacrilato. Dado que la colmatación de proteínas es ampliamente modelada, Bolton et al. (2005) estudió la microfiltración de soluciones proteicas (BSA y plasma humano) partiendo de los modelos clásicos de colmatación por bloqueo de poro para proponer cinco nuevos modelos resultantes de combinar las cuatro leyes ya mencionadas. En su análisis se prueba que la combinación bloqueo completo–formación de torta filtrante presenta el mejor ajuste con los resultados experimentales realizados con membranas polisulfonas.
Recientemente Duclos-Orsello et al. (2006) desarrollaron un modelo que integra todas las leyes de bloqueo en una sola ecuación con parámetros característicos de cada una. El modelo describe la colmatación en tres pasos: primero se produce la constricción del poro reduciendo el tamaño del interno; luego el bloqueo del poro ocurre en la superficie de la membrana previniendo la colmatación en la estructura interior. Finalmente, los colmatantes en la superficie de la membrana forman una torta, la cual controla las últimas etapas de la filtración. El modelo se valida con datos experimentales obtenidos por microfiltración de microesferas de poliestireno con membranas tipo Isopore y Durapore.
Modelos de polarización de la concentración (PC)
Este fue uno de los primeros modelos macroscópicos de filtración tangencial basados en la difusión molecular sobre la membrana, también conocido como teoría de la película (Ripperger y Altmann, 2002). La acumulación de las partículas retenidas sobre la superficie de la membrana es controlada por dos mecanismos opuestos de transferencia de masa (Wang y Song, 1999): convección de partículas hasta la superficie de la membrana, transportadas por el flujo de permeado y difusión hacia atrás de partículas desde la superficie de la membrana hacia el seno de la suspensión. En estado estacionario ambos mecanismos de transporte están balanceados, así (Ripperger y Altmann, 2002):
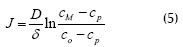
donde D: coeficiente de difusión, y δ: espesor de la capa de torta. La relación D/δ es generalmente dada en forma adimensional mediante el número de Sherwood. cP: concentración del componente a ser separado en el permeado, dada por las características de la membrana; c0: concentración en la alimentación, y cM: máxima concentración de partículas en el sistema. Todos los efectos de interacción de partículas, hidrodinámica y difusión se integran en el coeficiente de difusión, D.
Basados en esta teoría, algunos autores hacen descripciones más realistas del comportamiento de las partículas en suspensión. Song (1998a) expresó la ecuación de transporte en estado no estacionario y con ella analizó el bloqueo de poro y la formación de la torta durante la ultra y microfiltración de suspensiones de partículas de diferentes tamaños. En su modelo incluyó la caída de presión crítica cuando la capa de torta ya está presente sobre la superficie de la membrana, la cual se determina únicamente a partir de las propiedades termodinámicas de la suspensión y es independiente de la presión aplicada y del flux de permeado. Similarmente, Bacchin et al. (2002) introdujeron las fuerzas de interacción coloidal en la Ecuación (5) a través de la presión osmótica de la suspensión para describir la transición de la PC hasta la formación de la torta en un módulo membranario de geometría tubular. Las simulaciones en 3D fueron satisfactorias al compararlas con los datos resultantes de la experimentación con suspensiones coloidales de origen no biológico. Estas, y otras consideraciones acerca de la transferencia de masa y la hidrodinámica de la suspensión, hacen más complejos los modelos enunciados de manera que sean más útiles para describir la colmatación.
Song (1998b) desarrolló un modelo mecanístico de colmatación en estado no estacionario analizando el módulo desde una región de no equilibrio hasta una región de equilibrio. El modelo permite determinar el flux local de equilibrio Jeq, y el flux local J(t) en la región de no equilibrio con las siguientes ecuaciones, respectivamente:
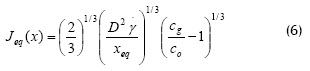
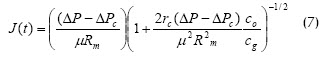
donde xeq: localización de la región de equilibrio en la dirección del flujo aguas abajo; c0 y cg: concentraciones de la solución alimentada y de la torta, respectivamente; γ tasa de corte, ΔP: caída de presión efectiva y ΔPc: presión crítica. La solución de este modelo da como resultado el tiempo para que el flux de permeado alcance el estado estacionario en el canal, tss. Una vez este valor es conocido, se puede calcular el flux promedio a lo largo del canal de longitud conocida. El modelo también permite calcular el espesor de la torta, δ (t), parámetro que es determinante en los resultados de estos estudios. Este modelo se validó usando suspensiones coloidales en sistemas de ultra y microfiltración tangencial. Es de gran utilidad a nivel industrial porque puede usarse en el diseño de módulos de filtración o en la optimización de las condiciones de operación para un proceso dado.
Modelos de difusión de corte inducido
Los modelos de difusión hidrodinámica de corte inducido están basados en las interacciones entre partículas inducidas por desplazamientos aleatorios dentro de las líneas de corriente. El primer modelo de este tipo, basado en la transferencia de masa clásica, fue propuesto por Zidney y Colton (1986), quienes asumieron que la difusividad de las partículas estaba dada por el coeficiente de difusión hidrodinámica de corte inducido (CDHCI) y no por el coeficiente de difusión molecular.
Para determinar el CDHCI, los primeros investigadores observaron que en una suspensión de esferas rígidas las partículas migraban atravesando las líneas de corriente en un campo de esfuerzo cortante uniforme producido por un dispositivo de Couette (Eckstein et al., 1977); midieron el grado de migración y propusieron una correlación empírica para el coeficiente de difusión (Ecuación (8)). Leigthon y Acrivos (1987) mejoraron esta propuesta y además desarrollaron una correlación para la viscosidad efectiva de una suspensión de esferas rígidas (Ecuación (9)).
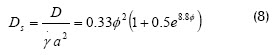

Donde Ds: coeficiente de difusión hidrodinámica de corte inducido, µ(Φ): viscosidad relativa de la suspensión, (Φ): fracción volumétrica de sólidos suspendidos y : radio de partícula.
Davis y colaboradores (Davis y Leighton, 1987; Davis y Sherwood, 1990) desarrollaron un modelo para describir el comportamiento de las partículas en la superficie de la membrana de un microfiltro de plato plano; el análisis considera las Ecs. (8) y (9) para describir el CDHCI y la viscosidad de partículas acumuladas en la capa estacionaria, respectivamente. Para el estudio usaron partículas monodispersas neutralmente suspendidas. Los resultados proporcionan una solución exacta del flux de permeado para suspensiones diluidas, y una solución precisa para un pequeño porcentaje de suspensiones no diluidas.
Basados en el mismo fenómeno hidrodinámico, Romero y Davis (1988) enuncian un primer modelo basado en la formación de una capa de torta estancada a partir de las partículas remanentes del flujo tangencial. Cuando esta capa alcanza un espesor máximo, el flux de permeado toma un valor cuasi estacionario independientemente de la variación en las condiciones de operación. Con un segundo modelo ahora en estado no estacionario, los mismos investigadores Romero y Davis (1990) predicen la estructura de la capa de torta formada en cualquier posición axial del filtro. El desarrollo de este modelo sugiere el uso de las correlaciones empíricas de Leighton y Acrivos (1987) dadas por las Ecs. (8) y (9). El trabajo de Romero y Davis es un buen análisis del transporte convectivo-difusivo de partículas porque predice satisfactoriamente la dinámica de la formación inicial de la torta y la del crecimiento de la torta estancada, lo que resulta en el decaimiento del flux de permeado. El modelo permite calcular el tiempo requerido para aproximarse al estado estacionario como una función de la resistencia específica de la torta y de la longitud del filtro. El flux en estado estacionario Jss, dependiente de la posición en el canal se puede obtener mediante la ecuación:
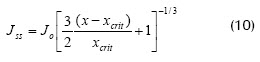
Donde, J0: flux del medio libre de partículas, x: distancia desde la entrada del canal, y xcrit: longitud de la zona libre de torta al comienzo de la membrana.
Kromkamp et al. (2005) examinaron la PC a partir de la hidrodinámica de la suspensión descrita por la difusión de corte inducido y la convección-difusión de partículas. Este trabajo es una aproximación más realista de la situación de colmatación de membranas causada por la PC porque considera el comportamiento de las partículas suspendidas en el flujo; la parte experimental se desarrolló usando una clase emergente de membranas de microingeniería llamadas microtamices con geometría de canal rectangular. Para las simulaciones usaron un esquema de diferencias finitas según el método reticular de Boltzmann (LB). Este modelo se destaca porque tiene aplicabilidad a sistemas con geometrías complejas y condiciones límites móviles.
Otro aporte a este tipo de modelos lo hicieron Lee y Clark (1998), quienes sugirieron que el crecimiento de la torta en un punto a lo largo del canal puede calcularse a partir de un balance másico pseudos estacionario de partículas por convección axial y por transporte difusivo. El cálculo de la acumulación másica de partículas en la superficie membranaria da una idea del decaimiento del flux de permeado durante la ultrafiltración tangencial de suspensiones de poliestireno monodisperso (látex). Para las simulaciones definen un coeficiente de difusión efectivo Def en dirección normal como la suma de los coeficientes de difusión molecular y el CDHCI, así:
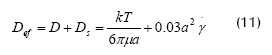
Donde k: constante de Bolztman y T: temperatura absoluta. Este modelo es una herramienta útil para investigar el efecto de diferentes variables de operación como tamaño de partícula, concentración de la alimentación, velocidad tangencial y dimensiones de la membrana. Además permite calcular de forma analítica el espesor de una torta homogénea cuando es difícil medirla físicamente. Según los autores, las simulaciones numéricas mostraron que la transferencia de masa alcanza el estado estacionario en muy poco tiempo, por eso no se consideró el estado transitorio.
También considerando el CDHCI, Mondor y Moresoli (2000) midieron la variación de la presión transmembranaria en cualquier posición axial de una membrana cilíndrica polisulfona de fibras huecas. El modelo contempla una resistencia intermedia causada por una capa estancada en la superficie de la membrana, tal como lo sugieren Romero y Davis (1988), la cual incrementa la resistencia total a la filtración del líquido y reduce el flux de permeado. Para el análisis consideraron tres regiones: flujo en el lumen (espacio entre la membrana y la pared capilar), flujo dentro de la membrana, y flujo en el espacio extracapilar. El coeficiente de difusión hidrodinámica de corte inducido se determina como:
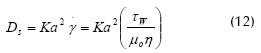
Donde K: función adimensional de la fracción volumétrica de partícula (Φ), µ0: viscosidad dinámica en la alimentación, η: viscosidad relativa adimensional, y Τw: esfuerzo de corte local en la pared. El modelo ofrece expresiones analíticas adimensionales para los perfiles de velocidad axial y radial en las zonas antes mencionadas, así como los perfiles de PTM a lo largo de la membrana. Teniendo en cuenta estas situaciones en el modelo global, se propone una ecuación mejorada para el flux de permeado en función de la posición axial, considerada de gran utilidad en el diseño de equipos.
Usando también la difusividad de corte inducido, Agashichev (2006) desarrolló un modelo para cuantificar la colmatación en membranas de microfiltración. El modelo involucra un conjunto de parámetros que han sido estudiados previamente por otros autores en forma individual y puede pronosticar la influencia de la tasa de corte en la polarización del gel, por lo que se considera de amplios alcances prácticos y simple ya que no requiere de integración numérica.
La mayoría de los estudios mencionados en esta sección aplican a suspensiones coloidales de sustancias no biológicas como el látex; por ello están restringidos a suspensiones de partículas rígidas y esféricas. La introducción de la concepción de capa estancada a lo largo de la membrana representa una alternativa para hacer una descripción más realista de la colmatación de la membrana.
Modelos de levantamiento inercial
En microfiltración tangencial de suspensiones coloidales se estudian dos grandes causas para la migración lateral: una fuerza de arrastre ejercida por el fluido sobre la partícula debido al flujo convectivo en la pared de la membrana que acarrea partículas hacia la membrana, Fd, y una fuerza inercial que acarrea partículas cerca de la membrana hacia afuera de la pared porosa, Fl.
El primer modelo, basado en la teoría de la elevación inercial, fue propuesto por Green y Belfort (1980), quienes asumieron que la fuerza lateral actuando sobre partículas simples se obtiene por adición vectorial de fuerzas inerciales. Estas fuerzas se derivan del movimiento de partículas en un ducto no poroso a partir de los términos no lineales de las ecuaciones de Navier-Stokes. Entonces, la fuerza lateral resultante y la fuerza de arrastre que permiten la permeación en un ducto poroso están dadas respectivamente por:
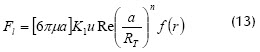
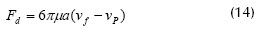
donde K1: coeficiente empírico adimensional, u: velocidad axial, Re: número de Reynolds, RT: radio del tubo, r: coordenada radial, n = 3; vf: velocidad de permeación, y vp: velocidad de partícula relativa a la velocidad de migración, vl. Estas fuerzas son importantes cuando el número de Reynolds expresado en términos del tamaño de las partículas es significante; también dependen de la velocidad de migración lateral y de la trayectoria de las partículas. El análisis indica que si las condiciones son tales que la velocidad de la elevación inercial es suficiente para compensar la velocidad del permeado oponente, entonces se espera que no haya depósito de partículas en la superficie de la membrana.
Una contribución a este modelo fue hecha por Altena y Belfort (1984), quienes determinaron la elevación inercial y el flujo de permeado para la migración lateral de esferas rígidas flotantes, fluyendo en flujo de Poiseuille en un ducto poroso con succión. Para el caso de una partícula esférica moviéndose sobre una pared porosa, el flux de permeado adimensional es:
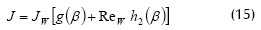
donde, β: distancia desde la pared porosa, Jw: velocidad de permeación en la pared (constante e independiente de la coordenada axial), h2(β): función del fluido no perturbado en la dirección lateral, g(β): función de flujo lateral, Rew: Reynolds en la pared porosa. Todos los términos anteriores están expresados en forma adimensional. Bajo condiciones típicas de flujo laminar, los autores encontraron que partículas con radio menor a 1 µm quedan retenidas en la superficie de la membrana, dando lugar a la formación de una torta o colmatación de la membrana.
Modelos de transporte superficial
Como una alternativa al transporte de partículas fuera de la membrana por mecanismos como la difusión y la elevación inercial, Mondor y Moresoli (2000) suponen que las partículas pueden acarrearse hacia la superficie de la membrana por el flujo de permeado y entonces rodar o deslizarse a lo largo de la superficie debido al flujo tangencial. Una aproximación continua de este modelo considera la formación de una capa de torta fluyente, considerada como la deposición simultánea de partículas en la capa de torta y en el flujo de esta capa hacia la salida del filtro. En la aproximación discreta, se considera una partícula esférica sobre la superficie de la membrana o en la superficie de una capa estancada; también las fuerzas actuantes y los balances de torque sobre la partícula para determinar si se adhiere a la superficie o se desplaza a lo largo de ella.
Considerando las fuerzas hidrodinámicas, adhesivas y de fricción de una partícula durante el proceso de microfiltración, Altmann y Ripperger (1997) introdujeron un modelo microscópico de la formación de la torta y su crecimiento; ellos balancearon las fuerzas de levantamiento inercial y las de arrastre (Ecs. 13 y 14) al filtrar suspensiones de partículas monodispersas usando membranas microporosas de poliamida. Según los autores, la estructura de la capa depende del periodo de arranque de la filtración y consideran la deposición de partículas un proceso irreversible ya que las fuerzas de adhesión y fricción son más altas que las fuerzas hidrodinámicas. También encontraron que el periodo estacionario depende especialmente del material fino del sistema de partículas, mientras que el no estacionario está influenciado por la distribución del tamaño de todas las partículas. Este modelo presenta resultados con muy buena precisión.
Partiendo de la probabilidad de adhesión de partículas, Stamatakis y Tien (1993) indicaron que la deposición de partículas ocurre una vez que la partícula toca un elemento rugoso de la superficie que es más alto que la altura crítica. Su modelo predice el flux de permeado con muy buena consistencia frente a los resultados experimentales obtenidos durante la microfiltración tangencial de suspensiones monodispersas de caolín usando membranas microporosas metálicas y poliméricas. La probabilidad de adhesión está dada por:
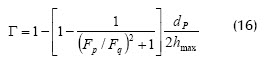
donde, Γ: probabilidad de adhesión; Fp: fuerza de arrastre en el campo del flujo de una partícula esférica; Fq: sumatoria de fuerzas debidas al levantamiento lateral (Ecuación (13)), al arrastre hidrodinámico (Ecuación (14)), y a la fuerza de flotación de partículas esféricas; hmax: altura máxima de protuberancia. La Ecuación (16) se incluye en el cálculo de la tasa dinámica de crecimiento del espesor de la torta δ (t), parámetro importante en la determinación del flux de permeado, expresado mediante la ley de Darcy de la forma:
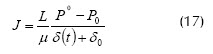
donde, L: permeabilidad de la torta, P0: presión de la suspensión, P0: presión aguas abajo de la membrana, y δ0: función del espesor y de la permeabilidad de la membrana.
Por su parte, Knutsen y Davis (2006) observaron el movimiento de las partículas mediante una técnica de visualización directa (DVO) y extendieron este concepto a un modelo dinámico para predecir no solo las condiciones requeridas para la deposición de partículas sino la velocidad promedio de rotación tangencial de las partículas colmatantes que interactúan con la superficie membranaria. El análisis está enfocado al balance de fuerzas normales y tangenciales dadas respectivamente por:
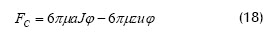
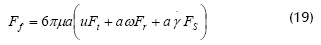
En la Ecuación (18), Fc: fuerza de contacto actuando sobre la esfera, z: distancia tangencial entre la aspereza mayor y la normal atravesando el centro de la esfera; φ: factor de corrección por la presencia de una superficie permeable. El primer término de la derecha es el arrastre de Stokes sobre la esfera debido al flujo de permeado, y el segundo término es la fuerza de lubricación sujeta a la constricción geométrica. En la Ecuación (19), Ff: fuerza de fricción, ω: velocidad rotacional de la esfera y Ft, Fr y Fs: coeficientes de resistencia para las fuerzas por traslación de partícula, rotación de partícula y corte del fluido, respectivamente.
Las condiciones para la colmatación sugieren que una partícula se depositará en la superficie de la membrana si su velocidad traslacional desaparece mientras está en contacto con la segunda aspereza más grande; entonces el flux se deriva de los balances de fuerzas y torques con v = 0:
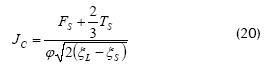
donde, Jc: flux de permeado crítico (adimensional); Ts: torque del fluido sobre la esfera debido al corte (igual a 0.9440); ξL y ξS: separaciones entre partícula y membrana basada en la rugosidad mayor y en la rugosidad menor, respectivamente. Las mediciones experimentales se realizaron con soluciones concentradas de levadura y suspensiones de microesferas de poliestireno (látex). Ambos resultados, experimental y teórico, mostraron que las partículas rodarán sobre la membrana más lentamente a fluxes de permeado más altos debido al incremento de las interacciones entre las partículas y las superficies rugosas de una membrana microporosa de disco de aluminio anodizado.
Existen otros modelos matemáticos hallados en la literatura enfocados hacia otros aspectos de interés como el flujo viscoso (Curcio et al., 2001; Nassehi, 1998; Wiley y Fletcher, 2003), el diseño (Cross, 2002; Hwang y Wu, 2007) y la distribución de los compuestos presentes (Djuric et al., 2004; Wang et al., 2005), pero por no involucrar el fenómeno de colmatación no se tuvieron en cuenta en esta revisión.
Conclusiones
En la literatura existen muy pocas revisiones comparativas sobre modelos matemáticos de la colmatación de membranas en MFT, pero se pueden encontrar modelos físicos independientes que proponen de diversas formas la descripción de dicho fenómeno. En gran parte de las publicaciones, el mecanismo de colmatación se ha relacionado con el decaimiento del flux de permeado involucrando diversos factores como las condiciones de operación, pretratamientos del alimento, morfología de la membrana, entre otros; sin embargo, se han hecho cada vez más importantes las teorías complejas sobre el comportamiento de una sola partícula en un sistema de flujo de partículas. Algunos modelos restringen los resultados a ciertas aplicaciones y geometrías del filtro, pero en general consideran mecanismos de transporte difusivo y convectivo o una combinación de ambos con el ánimo de representar la hidrodinámica del flujo a través de un medio poroso y representar realmente el proceso. Se nota además que cada vez se utilizan técnicas más modernas para observar las interacciones membrana-colmatante especialmente en la validación de los modelos microscópicos. No hay un modelo que involucre simultáneamente todas las variables que afectan el proceso; sin embargo, cada uno sugiere una buena concordancia con los resultados experimentales, de manera que se puede escoger el que mejor se acomode según la rigurosidad del caso. Un buen modelo para representar la colmatación de membranas durante los procesos de microfiltración tangencial es el de difusión hidrodinámica de corte inducido, ya que extiende la teoría del transporte difusivo de partículas con muy buena aceptación y puede usarse en diferentes aplicaciones y geometrías. Para el caso particular de los jugos de frutas, un modelo sencillo de PC es conveniente para describir la deposición de los polisacáridos insolubles en la superficie de la membrana a través del estudio de la resistencia de la torta, lo cual se logra con la determinación de la resistencia específica y el espesor de la misma; por supuesto, este enfoque depende del origen y la naturaleza de la fruta con que se preparen los jugos, ya que cada una tiene un comportamiento y una composición diferentes.
Nomenclatura
α radio de partícula
c constante en el modelo de bloqueo
c0 concentración de la solución alimentada
cg concentración de la torta gelificada
cM máxima concentración del sistema de partículas en flujo
cP concentración del componente a ser separado en el permeado
D coeficiente de difusión molecular
Def coeficiente de difusión efectivo
dp diámetro de partícula
Ds coeficiente de difusión hidrodinámica de corte inducido
Fc fuerza de contacto actuando sobre la esfera
Fd fuerza de arrastre sobre la partícula por convección en la pared de la membrana
Ff fuerza de fricción
Fl fuerza inercial que acarrea partículas hacia afuera de la pared porosa
Fp fuerza de arrastre de una partícula esférica en la sección del flujo
Fq sumatoria de fuerzas por levantamiento lateral, arrastre y empuje de esferas
Fr coeficiente de resistencia debido a la rotación de las partículas
Fs coeficiente de resistencia debido al corte del fluido
Ft coeficiente de resistencia debido a la traslación de la partícula
g(β) función de flujo lateral en la Ecuación (15)
h2(β) función del fluido no perturbado en dirección lateral
hmax altura máxima de protuberancia
i índice en la Ecuación (4)
J flux de permeado
J(t) flux local en la región de no equilibrio
J0 flux del medio libre de partículas
Jc flux de permeado crítico adimensional
Jeq flux local de equilibrio
Jss flux en estado estacionario
Jw flux en la pared
k constante de Bolztman
K función adimensional de la fracción volumétrica de partícula (?)
K1 coeficiente empírico adimensional
L permeabilidad de la torta
n índice en la Ecuación (13); n=3
P0 presión aguas abajo de la membrana
P0 presión de la suspensión
PTM presión transmembranaria
ΔP caída de presión efectiva en el canal
ΔPc presión crítica
r coordenada radial
Rad resistencia de adsorción de sustancias
Rb resistencia por bloqueo del poro
Rc resistencia de la torta
rc resistencia específica de la torta
Re número de Reynolds
Rew número de Reynolds en la pared de la membrana
Rg resistencia del gel
Rm resistencia intrínseca de la membrana
RT radio del tubo
Rt resistencia total
T temperatura absoluta
t tiempo de filtración
Ts torque del fluido sobre la esfera debido al corte (= 0.9440)
tss tiempo para que el fluxs de permeado alcance el estado estacionario
u velocidad axial
V volumen de filtrado por unidad de área de filtración
vf velocidad de permeación
vl velocidad de migración
vp velocidad de partícula relativa a la velocidad de migración
x distancia desde la entrada del canal
xcrit longitud de la zona libre de torta al comienzo de la membrana
xeq localización de la región de equilibrio en la dirección del flujo aguas abajo
z distancia tangencial entre la aspereza mayor y la normal desde el centro de la esfera
Símbolos griegos
φ factor de corrección por la presencia de una superficie permeable
β distancia desde la pared porosa
Φ fracción volumétrica de sólidos suspendidos
ε porosidad de la torta
µ viscosidad dinámica de la solución
µ(Φ) viscosidad relativa de la suspensión
µ0 viscosidad dinámica en la alimentación
δ espesor de la capa de torta
δ0 función del espesor y permeabilidad de la membrana
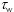 esfuerzo de corte local en la pared
esfuerzo de corte local en la pared
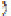 tasa de corte
tasa de corte
η viscosidad relativa
ω velocidad rotacional de la esfera
ξL separación entre partícula y membrana relativa a la rugosidad mayor
ξS separación entre partícula y membrana relativa a la rugosidad menor
Γ probabilidad de adhesión
Bibliografía
Agashichev, S. P., Concentration polarization in cross-flow microfiltration under the conditions of shear-induced diffusion., Desalination, 200, 2006, pgp. 346-348. [ Links ]
Altena, F. W., Belfort, G., Lateral migration of spherical particles in porous flow channels: applications to membrane filtration., Chem. Eng. Sci., 89 (2), 1984, pp. 343-355. [ Links ]
Altmann, J., Ripperger, S., Particle deposition and layer formation at the crossflow microfiltration., J. Memb. Sci., 124, 1991, pp. 119-128. [ Links ]
Bacchin, P., Si-Hassen, D., Starov, V., Clifton, M.J. y Aimar, P., A unifying model for concentration polarization, gel-layer formation and particle deposition in cross-flow membrane filtration of colloidal suspensions., Chem. Eng. Sci., 57, 2002, pp. 77-91. [ Links ]
Balakrishnan, M., Dua, M., Bhagat, J. J., Effect of operating parameters on sugarcane juice ultrafiltration: results of a field experience., Sep. Pur. Tech., 19, 2000, pp. 209-220. [ Links ]
Bird, M. R., Barttlet, M., Measuring and modelling flux recovery during the chemical cleaning of MF membranes for the processing of whey protein concentrate., J. Food Eng., 53, 2002, pp. 143-152. [ Links ]
Bird, R. B., Stewart, W. E., Lightfoot, E. N., Fenómenos de Transporte., Editorial Reverté, S.A., México, 1993. [ Links ]
Bolton, G., LaCasse, D., Kuriyel, R., Combined models of membrane fouling: Development and application to microfiltration and ultrafiltration of biological fluids., J. Memb. Sci., 277, 2005, pp. 75-84. [ Links ]
Carneiro, L., dos Santos Sa., I., dos Santos Gomes, F., Matta, V. M., Cabral., L. M. C., Cold sterilization and clarification of pinneapple juice by tangential microfiltration., Desalination 148, 2002, pp. 93-98. [ Links ]
Carrère, H., Blaszkowa, F., Roux de Balmann, H., Modelling the microfiltration of lactic acid fermentation broths and comparison of operating modes., Desalination, 145, 2002, pp. 201-206. [ Links ]
Choi, H., Zhang, K., Dionysiou, D. D., Oerther, D.B., Sorial, G. A., Influence of cross-flow velocity on membrane performance during filtration of biological suspension., J. Memb. Sci., 248, 2005, pp. 189-199. [ Links ]
Cross, R. A., Optimum process designs for ultrafiltration and crossflow microfiltration systems., Desalination, 145, 2002, pp. 59-163. [ Links ]
Cumming, I. W., Holdich, R. G., Ismail, B., Prediction of deposit depth and transmembrane pressure during crossflow microfiltration.. J. Memb. Sci., 154, 1999, pp. 229-237. [ Links ]
Curcio, S., Calabrò, V., Iorio, G., A theoretical analysis of transport phenomena in membrane concentration of liquorrice solutions: a FEM approach., J. Food Eng., 71, 2005, pp. 252-264. [ Links ]
Curcio, S., Calabrò, V., Iorio, G., Cindío, B., Fruit juice concentration by membranes: effect of rheological properties on concentration polarization phenomena., J. Food Eng., 48, 2001, pp. 235-241. [ Links ]
Davis, R. H., Leighton, D. T., Shear-induced transport of a particle layer along a porous wall., Chem. Eng. Sci. 42 (2), 1987, pp. 275-281. [ Links ]
Davis, R. H., Sherwood, J. D., A similarity solution for steady-state crossflow microfiltration., Chem. Eng. Sci. 45 (11), 1990, pp. 3203-3209. [ Links ]
Djuric, M., Gyura, J., Zavargo, Z., Seres, Z., Tekic, M., Modelling of ultrafiltration of non-sucrose compounds in sugar beet processing., J. Food Eng., 65, 2004, pp. 73-82. [ Links ]
Duclos-Orsello, C., Weiyi, L., Chia-Chi, H., A three mechanism model to describe fouling of microfiltration membranes., J. Memb. Sci., 280, 2006, pp. 856–866. [ Links ]
Eckstein, E. C., Bailey, D. G., Shapiro, A. H., Self diffusion of particles in shear flow of a suspension., J. Fluid Mech. 79, 1977, pp. 191-208. [ Links ]
Green, G., Belfort, G., Fouling of ultrafiltration membranes: lateral migration and the particle trajectory model., Desalination, 35, 1980, pp.129-147. [ Links ]
Hermia, J., Constant pressure blocking filtration law: Application to power law non-newtonians fluids., Trans. I. Chem. E., 60, 1982, pp.183-188. [ Links ]
Hwang, K-J., Lin, T-T., Effect of morphology of polymeric membrane on the performance of cross-flow micro-filtration., J. Memb. Sci. 199, 2002, pp. 41-52. [ Links ]
Hwang, K.-J., Wu, R.-M., Use of models in the design of cross-flow microfilters for the purification of protein from bio-mixtures., J. Chin. Inst. Chem. Eng. ARTICLE IN PRESS. [ Links ]
Jiraratananon, R., Chanachai, A., A study fouling in the ultrafiltration of passion fruit juice., J. Memb. Sci. 111, 1996, pp. 39-48. [ Links ]
Jonsson, G., Prádanos, P., Hernández, A., Fouling phenomena in microporous membranes., Flux decline kinetics and structural modifications. J. Memb. Sci. 112, 1996, pp. 171-183. [ Links ]
Kawakatsu, T., Nakajima, M., Nakao, S., Kimura, S., Threedimensional simulation of random packing and pore blocking phenomena during microfiltration., Desalination, 101, 1995, pp. 203-209. [ Links ]
Knutsen, J. S., Davis, R. H., Deposition of foulant particles during tangential flow filtration., J. Memb. Sci., 271, 2006, pp. 101-113. [ Links ]
Kromkamp, J., Bastiaanse, A., Swarts, J., Brans, G., van der Sman, R. G. M., Boom, R. M., A suspension model for hydrodynamics and concentration polarization in crossflow microfiltration., J. Memb. Sci. 253, 2005, pp. 67-79. [ Links ]
Lee, Y., Clark, M., Modeling of flux decline during crossflow ultrafiltration of colloidal suspensions. J. Memb. Sci. 149, 1998, pp. 181-202. [ Links ]
Leighton, D. T., Acrivos, A., Measurement of the shear induced coefficient of self-diffusion in concentrated suspendsions of spheres. J. Fluid Mech., 177, 1987, pp. 109-131. [ Links ]
Mondor, M., Moresoli, C., Experimental verification of the shear-induced hydrodinamic difusion model of crossflow microfiltration, with consideration the transmembrane pressure axial variation., J. Memb. Sci. 175, 2000, pp. 119-137. [ Links ]
Nassehi, V., Modelling of combined Navier-Stokes and Darcy flows in crossflow membrane filtration., Chem. Eng. Sci., 53 (6), 1998, pp. 1253-1265. [ Links ]
Riedl, K., Girard, B., Lencki, R. W., Influence of membrane structure in fouling layer morphology during apple juice clarification., J. Memb. Sci., 139, 1998, pp. 155-166. [ Links ]
Ripperger, S., Altmann, J., Crossflow microfiltration – state of art., Sep. Pur. Tech., 26, 2002, pp. 19-31. [ Links ]
Romero, C. A., Davis, R. H., Global model of crossflow microfiltration based on hydrodynamic particle diffusion., J Memb. Sci., 39, 1988, pp. 157-185. [ Links ]
Romero, C. A., Davis, R. H., Transient model of crossflow microfiltration., Chem. Eng. Sci., 45 (1), 1990, pp. 13-25. [ Links ]
Song, L., A new model for the calculation of the limiting flux in ultrafiltration., J. Memb. Sci. 144, 1998a, pp, 173-185. [ Links ]
Song, L., Flux decline in crossflow microfiltration and ultrafiltration: mechanisms and modeling of membrane fouling., J. Memb. Sci. 139, 1998b, pp. 183-200. [ Links ]
Stamatakis, K., Tien, C., A simple model of cross-flow filtration based on particle adhesion., AIChE J., 39 (8), 1993, pp.1292-1302. [ Links ]
Thomassen, J. K., Faraday, D. B. F., Underwood, B. O., Cleaver, J. A. S., The effect of varying transmembrane pressure and crossflow velocity on the microfiltration fouling of a model beer., Sep. Pur. Tech., 41, 2005, pp. 91-100. [ Links ]
Vaillant, F., Cisse, M., Chaverri, M., Perez, A., Dornier, M., Viquez, F., Dhuique-Mayer, C., Clarification and concentration of melon juice using membrane processes., Inn. Food Sci. Eng. Tech., 6, 2005, pp. 213-220. [ Links ]
Vaillant, F., Perez, A.,M., Viquez, F., Microfiltración tangencial: una alternativa innovadora para la transformación de frutas tropicales., La Alimentación Latinoamericana 252, 2004, pp. 38-46. [ Links ]
Vaillant, F., Millan, A., Dornier, M., Decloux, M., Reynes, M., Strategy for economical optimisation of the clarification of pulpy fruit juices using crossflow microfiltration. J. Food Eng., 48, 2001, pp. 83-90. [ Links ]
Vaillant, F., Millán, P., OBrien, G., Dornier, M., Decloux, M., Reynes, M., Crossflow microfiltration of passion fruit juice after partial enzymatic liquefaction., J. Food Eng., 42, 1999, pp. 215-224. [ Links ]
Vélez, C., Franco, E., González, J. A., Nuevos procesos membranarios aplicados a frutas tropicales-Ajustes hacia la fase industrial., Informe final de la automatización. Proyecto COLCIENCIAS-UNIVALLE-CIRAD-PASSICOL, Cali, 2007. [ Links ]
Vyas, H. K., Bennett, R. J., Marshall, A. D., Performance of crossflow microfiltration during constant transmembrane pressure and constant flux operations., Int. Dairy J. 12, 2002, pp. 473-479. [ Links ]
Wang, B. J., Wei, T. C., Yu, Z. R., Effect of operating temperature on component distribution of West Indian cherry juice in a microfiltration system., LWT, 38, 683-689, 2005. [ Links ]
Wang, L., Song, L., Flux decline in crossflow microfiltration and ultrafiltration: experimental verification of fouling dynamics., J. Memb. Sci., 160, 1999, pp. 41-50. [ Links ]
Wiley, D. E., Fletcher, D. F., Techniques for computational fluid dynamics modeling of flow in membrane channels., J. Memb. Sci., 211, 2003, pp. 127-137. [ Links ]
Ye, Y., Le Clech, V., Fane, A. G., Evolution of fouling during crossflow filtration of model EPS soluctions., J. Memb. Sci., 264, 2005, pp. 190-199. [ Links ]
Youn, K-S., Hong, J-H., Bae, D-H., Kim, S-J., Kim, S-D., Effective clarifying process of reconstituted apple juice using membrane filtration with filter-aid pretreatment., J. Memb. Sci., 228, 2004, pp. 179-186. [ Links ]
Yu, J., Lencki, W., Effect of enzyme treatments on the fouling behavior of apple juice during microfiltration., J. Food Eng., 63, 2004, pp. 413-423. [ Links ]
Zydney, L., Colton, C. K., A concentration polarization model for the filtrate flux in crossflow microfiltration of particulate suspensions., Chem. Eng. Comm., 47, 1986, pp. 1-21. [ Links ]














