Hugo Aya B.¹, Ricardo Cano M.², Petr Zhevandrov B.³

¹ Physicist and M.Sc., in Physical-Mathematics, Kishinev State University, Moldova. M.Sc., in Electric Engineering, Universidad de los Andes, Colombia. Professor, Universidad Distrital Franscisco José de Caldas, Colombia. haya@udistrital.edu.co

² Mathematician and M.Sc., in Mathematics, Universidad Nacional de Colombia.Professor, Universidad de la Sabana, Colombia. ricardo.cano@unisabana.edu.co

³ Ph.D., in Physical-Mathematics Sciences, Moscow State University, Russian. Professor, Universidad de la Sabana, Colombia. petr.zhevandrov@unisabana.edu.co

ABSTRACT

This paper has studied the problem of natural frequencies for Euler-Bernoulli beams having non-uniform crosssection. The numerically-obtained solutions were compared to asymptotic solutions obtained by the Wentzel- Kramers-Brillouin (WKB) method. It was established that WKB formula precision was higher than 3% for high frequencies (≥ 4 mode).

Keywords: Euler-Bernoulli beam, WKB method.

Received: september 91th 2009. Accepted: febrary 10th 2011

Introduction

Non-uniform beams’ viations have been studied since the 19th century (e.g. Todhunter, 1893, §1302 about Kirchhoff's research). More recent studies can be consulted in (Aate, 1995) and (Hsu-Lai-Chen, 2008) where relevant references and a review of results can be found. Natural Euler-Bernoulli (EB) beam frequencies were obtained in (Aate, 1995) for a special case of coefficients when EB equation solution was expressed in elementary functions.

For the non-uniform rod (Sturm-Liouville problem) equation with variable density or cross-section, when the equation cannot be integrated, even in terms of special functions, one can use the Wentzel-Kramers-Brillouin (WKB) method, also known in the literature as the Liouville-Green approximation (Akulenko- Nesterov, 2005; Geist-McLaughlin, 2001) to find high frequency asymptotics. This method consists of obtaining asymptotic series for solutions in powers of the corresponding small parameter. This technique was applied to the 4th order EB equation (by contrast with the 2nd order rod equation), although the WKB method is developed for nth order equations (Fedoryuk, 1993).

The results of this application are presented in this paper. The WKB method gave results coinciding with numerical results having less than 3% error for mode number 4, and this error became reduced for higher modes.

Asymptotic solution for a non-uniform beam

The transversal viations for a non-uniform beam in a Euler-Bernoulli approach have been described by (Tijonov-Samarsky,1972)

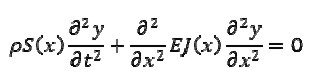[1]

where E was the Young modulus of the beam ρ, was its density, S(x) was the cross-sectional area, J(x) was the moment of cross-section inertia regarding its horizontal axis and y was transversal displacement. Variation of density ρ regarding x could be included in coefficient S(x) It was assumed that functions S(x) and J(x) were smooth and positive for 0 ≤ x ≤ l, where l was the length of the beam.

Natural viation modes for the beam could be expressed as

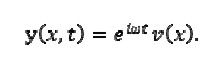
The following was obtained by substituting in equation (1)

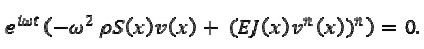
Equation (1) thus became transformed into the following equation

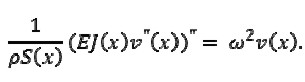[2]

For the boundary conditions formulated in section 3 (see below), eigenvalues w = w_n for (2) tended to infinity as n → ∞(Akulenko-Nesterov, 2005); therefore, ε = w^{- 1/2} _n → 0, as n → ∞ and ^ε could be considered as a small parameter for the problem.

The WKB method

Following the traditional WKB method, the solution of equation (2) could be as follows

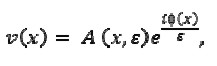[3]

where

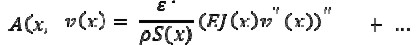
and unknown functions Φ(x) and A_j(x), j = 0,1,2,...were smooth.

If w² = 1 / ε⁴ then equation 2 would become transformed to

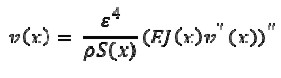
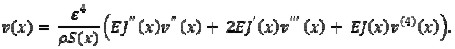[4]

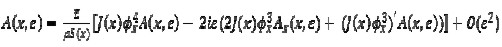[5]

After some computation, (3) and (4) would be obtained

Separating terms having equal powers of ε, the following would be obtained

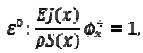[6]

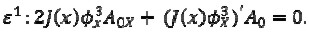[7]

From equations for coefficients εⁿ, n ≥ 2 , equations for A_{n - 1}(x) could be obtained, having the same form as (7) with terms depending on A_j, j ≤ n - 2, on the right-hand side.

From equation (6), it followed that

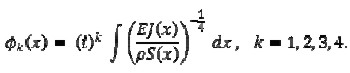[8]

From equation (7) it followed that

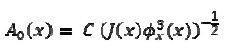[9]

Where C was an arbitrary constant.

Therefore, substituting (8) in (9), function A₀(x) could be expressed in the following form

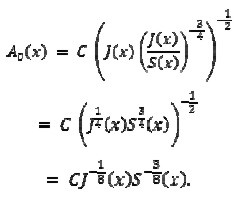[10]

Hence, solution v(x) for (2) could be written as

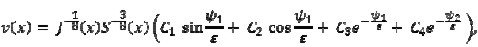[11]

Where

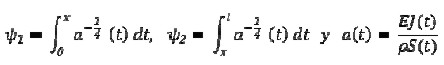
Formula (11) would represent a linear combination of four functions approximating the four linearly independent solutions for equation (2) (Fedoryuk, 1993).

In cases when the solution of (2) could be obtained exactly in terms of elementary functions (when S, J were constants, uniform beam; or S = S₀ (1 + αx)⁴, J = J₀ (1+ αx)⁴ ; in the latter case (Aate, 1995), substitution w(x) = (1 + αx)² v(x) would reduce the equation to a uniform beam), WKB solutions coincided with exact solutions; in such cases, corrections to amplitudes A_n. n ≥ 1 removed identically.

Equation for natural frequencies

To complete formulating the problem, boundary conditions for function v(x) in (2) were specified for a clamped beam and a cantilevered beam.

Clamped beam

The boundary conditions in this case were given by

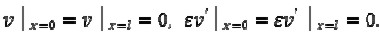[12]

Non-uniform beam

Substituting solution (11) in boundary conditions (12), a homogeneous system of four equations was obtained for coefficients Ci, i= 1,2,3,4 This system had nontrivial solutions when

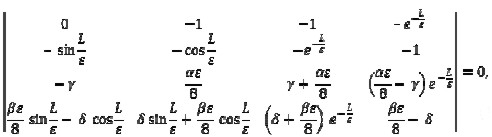[13]

Where

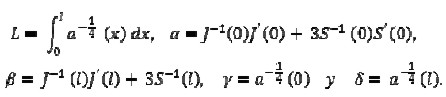
Equation (13) was the secular equation for natural frequencies w_n = ε^-2

Uniform beam

If the beam were uniform, then γ = δ, α = 0 and β; = 0, hence the determinant in (13) would become

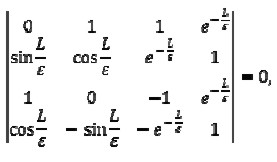[14]

implying that

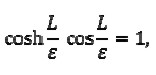
and this would coincide with the classical result (Landau-Lifshitz, 1975).

Truncated WKB formulas

Strictly speaking, the asymptotics for a fundamental system of solutions having accuracy 0(ε) have been obtained; therefore, terms for this and higher orders must be discarded (for example, e^{- L/ε} = 0(ε^∞)) in (13). This significantly simplifies the calculations. The determinant in (13) would thus become

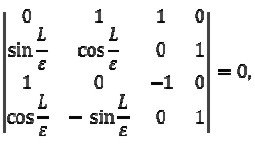[15]

implying

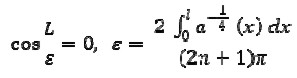
and thus

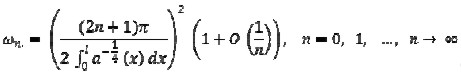[16]

The latter result has been called WKB(t) for "truncated". Nevertheless, it turned out that (13) gave a better approximation to the eigenvalues, as will be seen in section 3.3. The fact that 0(ε) order terms in (13) were retained was not rigorously justified; however, their inclusion did not present additional difficulties in obtaining w_n surely did not worsen the result. Solutions for (13) had the same property (16) as solutions for (15) and could be more useful in practice. It should be emphasised that truncated formulas do not become exact formulas when a problem requires an exact solution; by contrast, formula (13) did become the exact secular equation in cases when the latter was known (e.g., constant coefficients).

Cantilevered beam

The boundary conditions for a cantilevered beam⁴ were given by

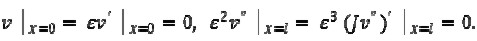[17]

Uniform beam

Similarly to the previous case, substituting solution (11) in boundary conditions (17), led to obtaining a homogeneous system of four equations for coefficients Ci, i=1,2,3,4 .

This system had nontrivial solutions when

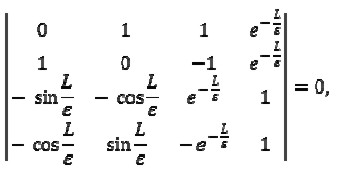[18]

Implying

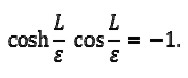
WKB(t) formulas

Just as in subsection 3.1.3, discarding O(ε) terms as well as those of higher orders in (18), led to

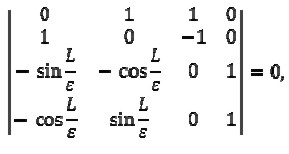[19]

Implying

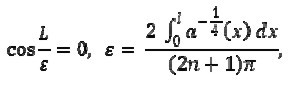
and obtaining the same result (16):

Other boundary conditions could be considered.

Results

The non-dimensional frequencies for the first six viation modes for a 1 m length conical beam were obtained by using ANSYS simulation package and WKB and WKB(t) formulas. In this case, radius would be (in millimetres r (x)= 1 +nx

with n = 1, 5 , 9 (x in meters).

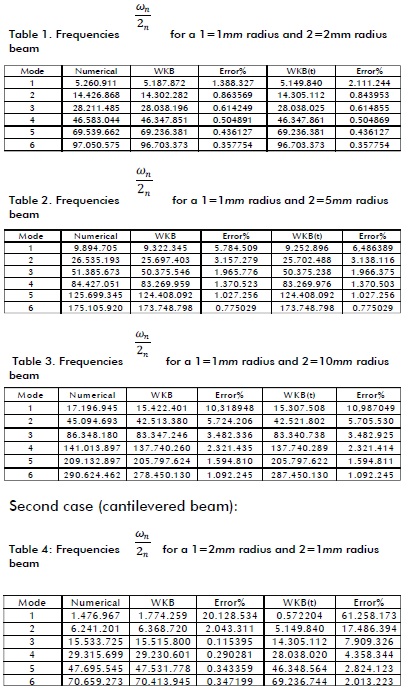
The first three Tables give the results for a clamped beam, with left end radius being 1 mm and right end 2, 5 and 10 mm.

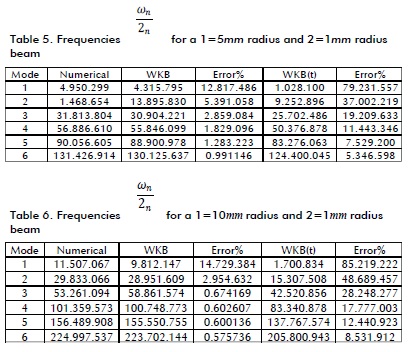
The last three Tables show the results for a cantilevered beam whose left end was clamped and had 2, 5 and 10 mm radius, the right end being free and 1 mm radius.

Radius 1 means left-end radius and radius 2 the right end in all Tables.

First case (clamped beam):

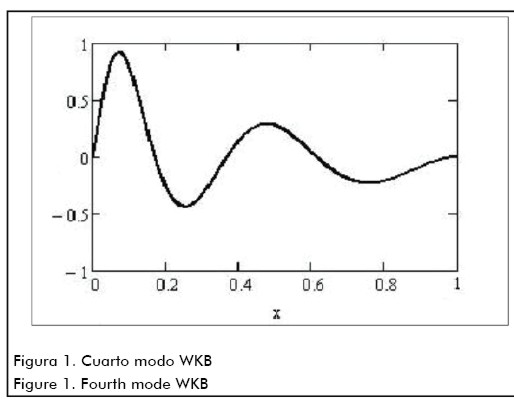
As an example, graphs are presented for 4^th mode eigenfunctions in the case of a cantilevered beam having 1=1mm radius and 2=10mm radius obtained by the WKB method and the ANSYS package.

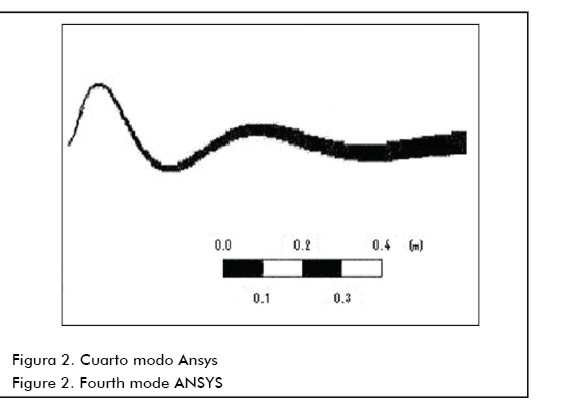
Conclusions

The numerical results given in Section 3.3 showed that the WKB approach provided natural frequency values having higher than 3% precision, even for modes having numbers n ≥ 4. It is worth noting that the finite element method for high frequencies (e.g. n ≥ 10 ) led to serious problems in applications. Standard programmes for n ≥ 10 revealed computational instability. It was clearly seen that retaining the exponentially small terms in secular equation (WKB formulas compared to WKB(t) formulas) substantially improved the numerical results. Although this conclusion was not a consequence of rigorous analysis, it seemed natural because WKB formulas (as opposed to WKB(t)) become part of an exact secular equation in the case of constant coefficients and in the only known case (Aate,1995) when the solution can be expressed in terms of elementary functions.

Acknowledgements

H. Aya would like to acknowledge partial financial support from the Universidad Distrital's Engineering Faculty's Electronic Engineering Curricular Project

R. Cano and P. Zhevandrov would like to acknowledge partial financial support from the Universidad de La Sabana, project ING-112, and P. Zhevandrov acknowledges the support of CONACYT (México), project 61351.

Foot Note

4 Clamped left end, free right end.

References