Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.33 no.3 Bogotá Sept./Dec. 2013
J. D. Aristizabal-Ochoa1
1 J. Dario Aristizabal-Ochoa. MS, PhD, University of Illinois at Champaign-Urbana, USA. Affiliation: Full Professor, Dept. of Civil Engineering, Universidad Nacional de Colombia, Medellin, Colombia. E-mail: jdaristi@unal.edu.co.
How to cite: Aristizabal-Ochoa, J. D., Stability of slender columns on an elastic foundation with generalised end conditions., Ingeniería e Investigación, Vol. 33, No. 3, December 2013, pp. 34 - 40.
ABSTRACT
Slender columns' lateral stability under compressive axial loads is presented, with uninhibited, partially inhibited and totally inhibited end side-sway, including the effects of semi-rigid connections and a uniformly distributed lateral elastic foundation (Winkler's type) throughout its entire span. The proposed classification of prismatic columns on an elastic foundation and the corresponding stability equations are general and relatively simple to apply, yielding exact results when compared to other analytical methods. The buckling load was obtained by making the determinant of a 4 x 4 matrix equal to zero for columns having side-sway uninhibited or partially inhibited at both ends, and of a 3 x 3 matrix for columns having side-sway inhibited at one or both ends. The effect of semi-rigid connections on the buckling load of five classical column cases is fully discussed and the results compared to those arising from other analytical methods.
Keywords: bracing, buckling, column, elastic foundation, pile, semi-rigid connection, stability.
RESUMEN
Se presenta de una manera clásica la estabilidad lateral de columnas esbeltas bajo cargas axiales de compresión; con derivas en los extremos desinhibidas, inhibidas parcialmente y totalmente inhibidas, incluyendo los efectos de las conexiones semirrígidas y una fundación elástica lateral y uniformemente distribuida (tipo Winkler) a lo largo de toda su luz. La clasificación propuesta en las columnas prismáticas, sobre fundación elástica y las ecuaciones correspondientes de estabilidad son generales y relativamente simples de aplicar; obteniéndose resultados exactos cuando se comparan con otros métodos analíticos. La carga de pandeo se obtiene igualando a cero el valor del determinante de una matriz de 4 x 4, para columnas con deriva lateral desinhibida o parcialmente inhibida en ambos extremos, y de una matriz de 3 x 3 para columnas con deriva lateral inhibida en uno o ambos extremos, respectivamente. Los efectos de las conexiones semirrígidas sobre la carga de pandeo, de cinco casos de columna clásicos, son discutidos y los resultados son comparados con los de otros métodos analíticos.
Palabras clave: arriostramiento, pandeo, columnas, fundación elástica, pilas, conexiones semirrígidas y estabilidad.
Received: May 19th 2013 Accepted: October 15th 2013
Introduction
The stability and second-order static analysis of columns laterally supported on an elastic foundation in generalised end conditions are of importance whit structural engineering. As noted by Hetenyi (1967), there are many applications for such analysis, such as the construction of pile foundations, railroad tracks, bridges, thin revolution shells (pressure vessels, boilers and containers) and large-span cylindrical shells and domes. For instance, a symmetrically loaded longitudinal element of a cylindrical tube regarding its axis can be treated as a beam on an elastic foundation. Thus, the proposed approach can be used for studying a wide range of problems related to elastic stability and second-order static analysis, being of particular importance in structural and geotechnical engineering, specifically in soil-structure interaction problems dealing with piles, drilled shafts, caissons and/or piers subjected to a combinations of axial, moment and lateral loads.
Hetenyi (1967) outlined the classical procedure for resolving the elastic stability of prismatic columns having hinged and clamped connections on an elastic foundation presenting the "exact" solution for particular cases, such as columns having free-free, hinged-hinged and clamped-clamped end conditions. Timoshenko and Gere (1961) used a similar approach to resolving other cases of interest, such as a column under a uniformly-distributed axial load on an elastic foundation. West and Mafi (1984) determined the eigen-values for columns on elastic supports using an initial-value numerical method. Razaqpur (1986) presented the stiffness and equivalent joint load matrices for a column finite element resting on a Winkler-type elastic foundation using "exact" shape functions. Cheng and Pantelides (1988) derived the differential equations, stiffness coefficients and fixed-end forces of a column on an elastic foundation, including bending and shear deformation. Ang and Wang (1990), as well as Wang, Xiang and Kitipornchai (1991) used finite elements for studying the buckling of columns on an elastic foundation. More recent papers on the stability of beam-columns resting on an elastic foundation, including two and three parameter foundation models, are available in the technical literature, such as those by Struthers and Jayaraman (2010), Morfidis (2007, 2010), Avramidis and Morfidis (2006) and Onu (2006).
Aristizabal-Ochoa (1994, 1996 and 1997) has presented the effects of semi-rigid connections on the stability and second-order analysis of columns and framed structures. Areiza-Hurtado et al., (2005) evaluated second-order stiffness matrix and loading vector with generalised end conditions regarding a Timoshenko column on a Winkler foundation. More recently, Arboleda-Monsalve et al., (2008) and Zapata-Medina et al., (2010) have studied shear effects on elastic stability and the dynamics of beams-columns on an elastic foundation. However, a complete set of stability equations for columns laterally supported on a continuous elastic foundation having generalised end conditions subjected to axial end loads are not available in the technical literature.
This publication's main objective was thus to present complete classification and corresponding stability equations for prismatic columns subjected to end axial loads, including the effects of semi-rigid bending connections, bracing stiffness at both ends and a uniformly distributed elastic support (Winkler type). The buckling load was obtained by making the determinant of a 4´4 matrix equal to zero for columns having side-sway uninhibited or partially inhibited at both ends, and of a 3´3 matrix for columns having side-sway inhibited at one or both ends. The present paper is restricted to an elastic static analysis of a single slender column, with three different lateral bracing types, leading to manageable analytical solutions. The effects of shear deformation on the member's buckling capacity are neglected. The importance of shear effects on the static and dynamic response of short columns or columns with low shear stiffness [Areiza-Hurtado et al (2005), Arboleda-Monsalve et al., (2008), and Zapata-Medina et al. (2010)].
Structural model
Assumptions
A prismatic element is considered that connects points A and B (Fig. 1). AB consists of a column A'B' and lumped flexural connectors AA' and BB' at the top and bottom ends, respectively. It is assumed that:
- A'B' is made from a homogeneous linear elastic material having a modulus of elasticity E and continuously supported along its span by a uniformly distributed elastic foundation (Winkler type) of magnitude ks;
- The centroid axis of the column is initially a straight line in which the elastic centroid coincided with the shear centre of the cross section. Initial geometrical imperfections in the column were not considered;
- The column is subject to end compressive axial load P applied along its centroid axis and also subjected to overturning moments and shear forces Ma, Va and Mb, Vb at ends A' and B', respectively;
- End lateral sway is partially inhibited by springs Sa and Sb located at A' and B', respectively;
- End rotations are partially inhibited by flexural springs kaand kb located at A' and B', respectively; and
- The second-order analysis in the next section is intended to be in the small deflection range (commonly referred to as a "linearised" approach). It should be pointed out that results are valid as long as the lateral deflection of the column remained small.
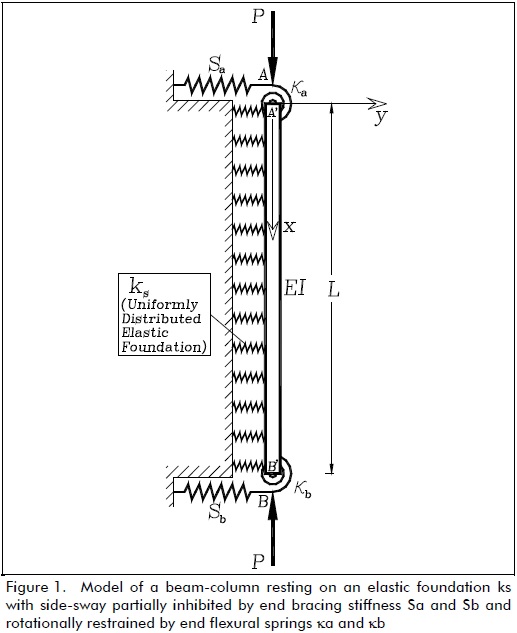
Flexural connectors AA' and BB' had stiffness ka and kb (with units in force-distance/radian), respectively. The ratios Ra= ka/(EI/L) and Rb= kb/(EI/L) were denoted as the stiffness indices of the flexural connections, where I = column moment of inertia about the principal axis in question and L = column span. The stiffness indices varied from zero (i.e. Ra= Rb= 0) for hinged connections to infinity (i.e., Ra= Rb= ∞) for rigid connections or clamped ends.
The main difference between the classical solution presented in this paper and that available in the pertinent technical literature (Timoshenko and Gere, 1961; Hetenyi, 1967; Scott, 1981) is that the solution for the model shown in Fig. 1 included the effects of semi-rigid connections and could be used for both stability and second-order analysis of columns on an elastic foundation subjected to any end load combination.
For convenience, the following two parameters were introduced:
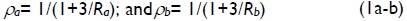
where ρa and ρb were called fixity factors. For perfectly hinged connections, both fixity factor ρ and stiffness index R were zero; but, for perfectly rigid connections, fixity factor was 1 and the stiffness index was infinity. Since fixity factor in the elastic range can only vary from 0 to +1 (while stiffness index R may vary form o to +∞), it was more convenient to use it in the analysis of structures having semi-rigid connections, as suggested by Monforton (1963). Factor 3 in equations (1a-b) came from the slope-deflection analysis of a beam having semi-rigid connections at both ends.
Deriving lateral equilibrium equations
The second-order governing of a differential equation for a prismatic column laterally supported on an elastic foundation ks subjected to compressive axial loads P at both ends as well as to overturning moments and shears Ma, Va and Mb, Vb at A' and B', respectively, is as follows:

Eq. (2) is the equation governing a column laterally supported on an elastic foundation subject to compressive axial loads P at both ends in deformed conditions. Its solution is known as second-order analysis (see Chen and Lui, 1987, p. 2).
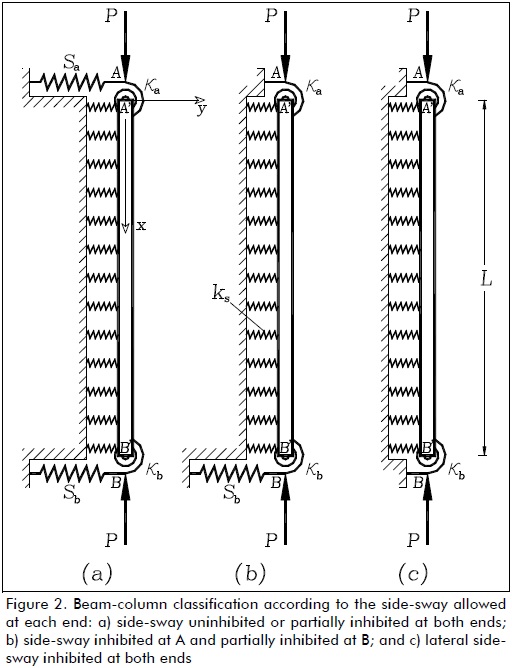
For a column having side-sway partially inhibited at both ends (Fig. 2a), the solution to Eq. (2) has to be subject to the following four boundary conditions:
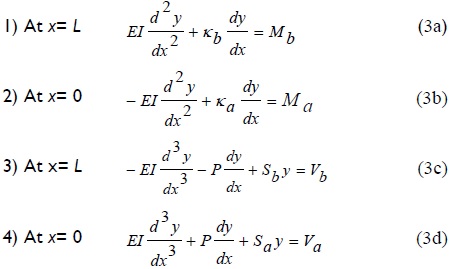
The solution to Eq. (2) depends on the relative value of compressive P regarding  , as explained by Hetenyi (1967). There were two types of solution in the compressive range (i.e., for P > 0), as follows:
, as explained by Hetenyi (1967). There were two types of solution in the compressive range (i.e., for P > 0), as follows:
for 0 ≤ P < 
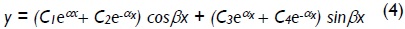
where: 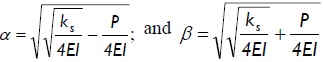
for P > 
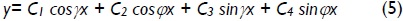
where: 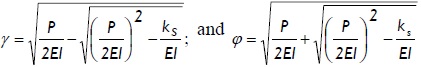
The four constants C1, C2, C3 and C4 in Eqs. (4) and (5) is determined from the four natural boundary conditions given by Eqs. (3a)-(3d). These is reduced to Eqs. (6a)-(6d) after some algebraic manipulation:
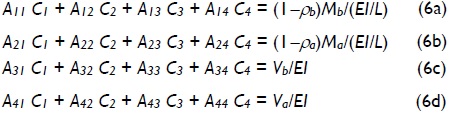
where Aij coefficients were as follows:
I) for 0 ≤ P < 
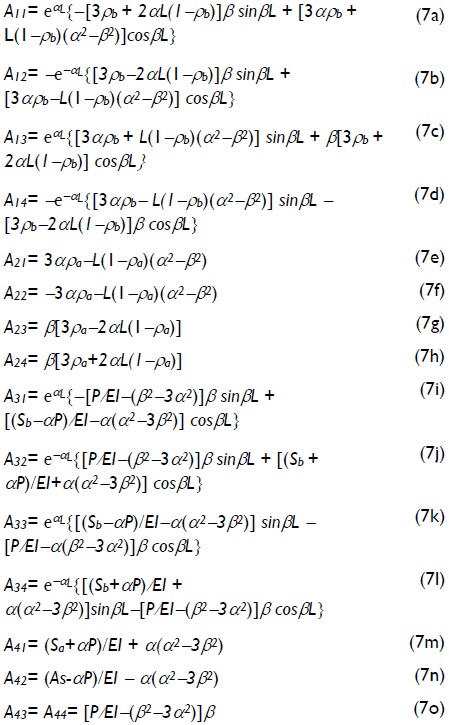
where: 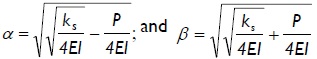
II) for P > 

where: 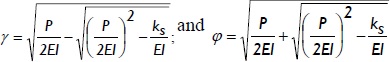
For columns having side-sway totally inhibited at A' and partially inhibited at B' (Fig. 2b), the fourth natural boundary condition given by Eq. (3d) or (6d) has to be substituted by forced boundary condition y = 0 at A or simple C1= -C2, which, when introduced into the other three natural boundary conditions given by Eqs. (6a)-(6c), became:
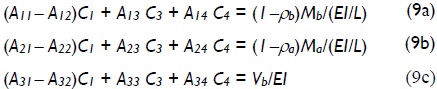
For columns having lateral side-sway totally inhibited at both ends A' and B' (Fig. 2c), the third natural boundary condition given by Eqs. (3c) or (9c) has to be substituted by forced boundary conditions y = 0 at B. This condition became:
for 0 ≤ P< 
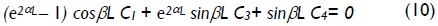
for P > 
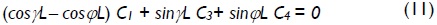
Proposed stability equations
According to the type of end side-sway just described, three major buckling modes is distinguished in columns having semi-rigid connections and being laterally supported on a continuous Winkler´s foundation. They were columns having lateral sway which was uninhibited or partially inhibited at both ends (Fig. 2a), totally inhibited at one end and partially inhibited at the other end (Fig. 2b) and/or totally inhibited at both ends (Fig. 2c). The corresponding stability equations are listed and explained below for easy reference:
Type 1: Columns with side-sway uninhibited or partially inhibited at both ends
For columns in which side-sway at A' and B' is partially inhibited by springs Sa and Sb (Fig. 2a), respectively, the stability equation consisted of the eigen-value solution to the 4x4 determinant given by Eq. (12):

Type 2: Columns having side-sway inhibited at one end and partially inhibited at the other end
For columns in which lateral sway at A' is totally inhibited and partially inhibited at B' by lateral spring Sb (Fig. 2b), the stability equation consists of the eigen-value solution to the 3x3 determinant given by Eq. (13):
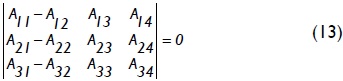
Type 3: Columns with lateral side-sway inhibited at both ends
For columns having lateral sway totally inhibited at both ends (Fig. 2c), the stability equation consists of the eigen-value solution to the 3x3 determinant given by Eqs. (14) or (15):
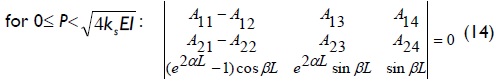
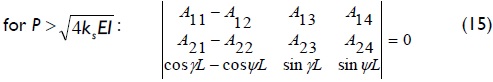
The Aij coefficients in Eqs. (12), (13), (14) and (15) is given by expression (7) or (8), depending on the magnitude of compressive load P when compared to  (the value of elastic buckling load of an infinitely long column, as explained by Hetenyi (1967), p. 136).
(the value of elastic buckling load of an infinitely long column, as explained by Hetenyi (1967), p. 136).
It may be noticed that the buckling modal shapes for any of the three types of buckling could be determined directly using either Eq. (4) or Eq. (5) once the value of the buckling load had been determined from the corresponding characteristic equations listed above (i.e. Eqs. (12)-(15)] and corresponding Aij coefficients given by either Eqs. (7) or (8) calculated). This solution was identical to that for any standard eigen-value problem.
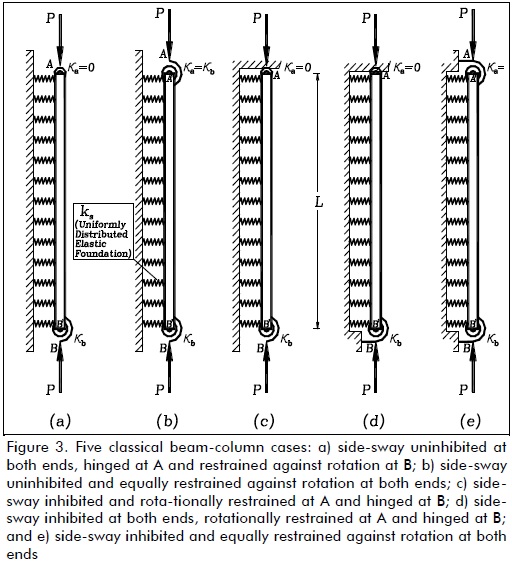
Classical column cases
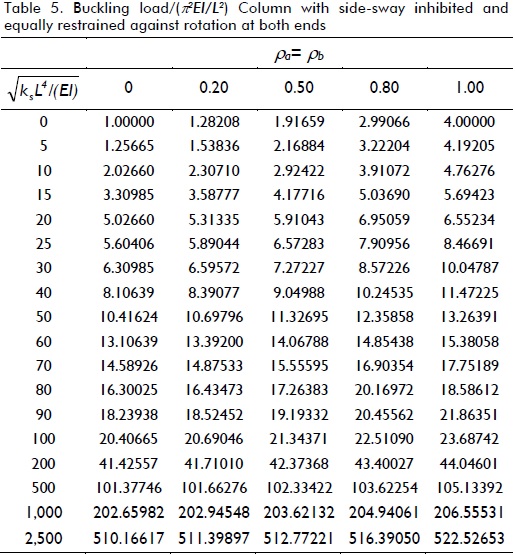
Variations in the critical load of a column supported by a uniformly distributed elastic foundation of stiffness ks under different boundary conditions (five cases shown in Fig. 3a-e), including the effects of semi-rigid connections, were studied. The critical loads for different values of 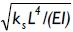 as suggested by Hetenyi (1967), and for five different fixity factors ranging from hinged to clamped conditions, are listed in Tables 1-5 for each case shown in Fig. 3a-e, respectively. The values listed in these tables were calculated to five significant figures (for comparison with those obtained by Hetenty's formulae) using the proposed model and Eqs. (12)-(15).
as suggested by Hetenyi (1967), and for five different fixity factors ranging from hinged to clamped conditions, are listed in Tables 1-5 for each case shown in Fig. 3a-e, respectively. The values listed in these tables were calculated to five significant figures (for comparison with those obtained by Hetenty's formulae) using the proposed model and Eqs. (12)-(15).
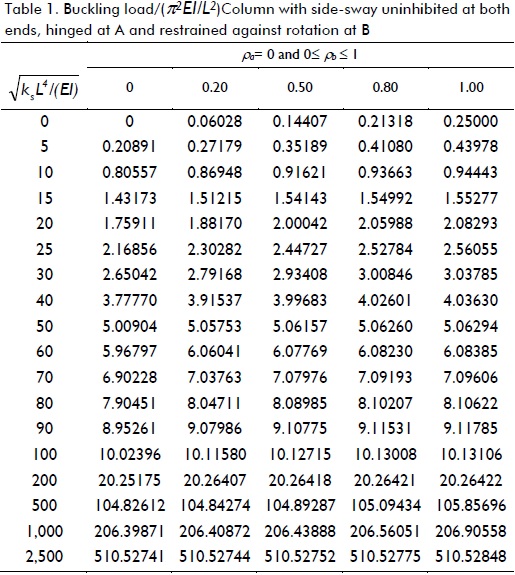
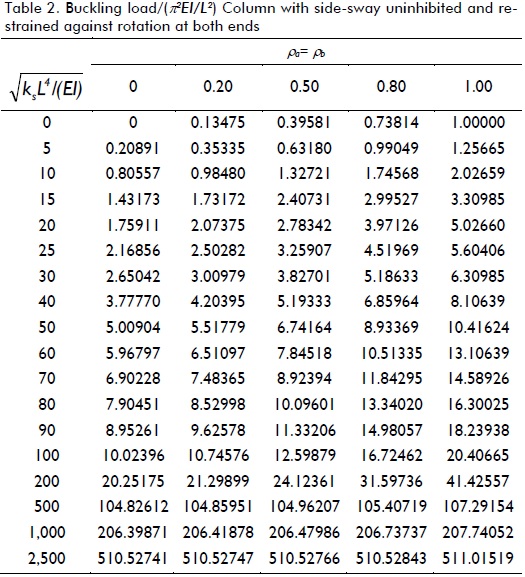
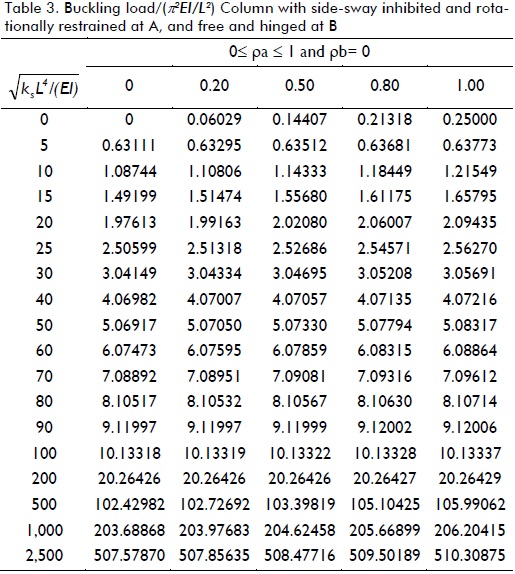
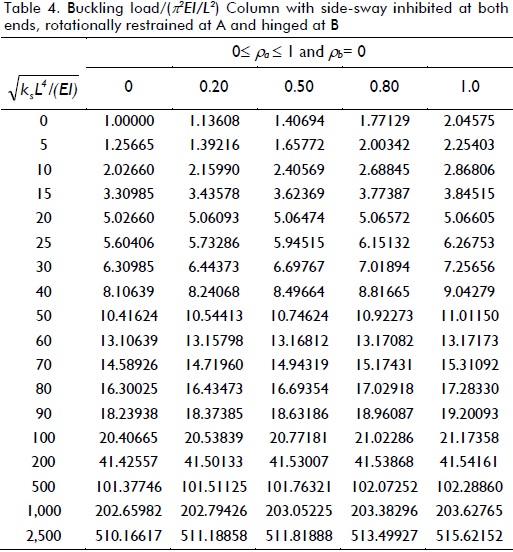
The values listed in Tables 1 and 2 for ρ = 0 (i.e. hinged) were verified with those by Hetenyi (1967) [Eq. 125 and Fig. 117, p. 143], yielding identical results, whereas those in Table 3 compared very well to the simplified formula 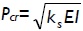 for infinitely long columns and any value of rotational restraint at B reported by Hetenyi (1967). Similarly, values listed in Tables 4 and 5 for ρ = 0 (i.e. hinged) and ρ = 1 (i.e. perfectly clamped) were verified with those by Hetenyi (1967) [Eqs. 127 and 128, and Figs. 118 and 119, respectively, pages 145-147], identical results being yielded too. The values in Table 4 also compared very well to the simplified formula
for infinitely long columns and any value of rotational restraint at B reported by Hetenyi (1967). Similarly, values listed in Tables 4 and 5 for ρ = 0 (i.e. hinged) and ρ = 1 (i.e. perfectly clamped) were verified with those by Hetenyi (1967) [Eqs. 127 and 128, and Figs. 118 and 119, respectively, pages 145-147], identical results being yielded too. The values in Table 4 also compared very well to the simplified formula 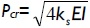 for infinitely long columns and any value of end rotational restraint reported by Hetenyi (1967).
for infinitely long columns and any value of end rotational restraint reported by Hetenyi (1967).
Table 1 indicates that for columns having side-sway uninhibited at both ends and rotational restraint at one end, it was only effective in columns on elastic foundations having ks< 25EI/L4. For larger values of ks, increased buckling load regarding rotational restraint was rather small (less than 20% for values of ks< 900EI/L4 and reaching increases lower than 3% for ks> 2500EI/L4). Table 2 indicates that critical load increased over 500% for ks< 25EI/L4 by perfectly clamping both ends as compared to perfectly hinged ends. For larger values of ks, the buckling load increased by just over 100%.
Table 3 indicates that for columns having side-sway inhibited at one end, rotational restraint at the same end was only effective in columns on an elastic foundation where ks ≈ 0. For 25EI/L4< ks< 400EI/L4 the increase in buckling load was less than 12% and for values of ks> 900EI/L4 the increase in buckling load was less than 1%.
Tables 4 and 5 indicate similar trends to those observed in Tables 1 and 2 for columns having side-sway inhibited at both ends. Rotational restraints at one or both ends were only effective in columns on an elastic foundation where ks< 25EI/L4. For larger values of ks, increased buckling load regarding rotational restraint was not significant. It was obvious that it was more effective to restrain both ends simultaneously against rotation than just one end. The values listed in Tables 1, 3 and 4 varied linearly with, having very small variations in Pcr with the degree of flexural restraint, making rotational conditions of secondary importance in long columns.
Summary and conclusions
An analytical method has been presented for evaluating the critical buckling axial load of columns having side-sway uninhibited, partially inhibited and totally inhibited and laterally supported by a uniformly distributed elastic foundation (Winkler's model). The proposed column classification and corresponding stability equations were general and relatively simple to apply, yielding exact results when compared to other linear elastic analytical methods. The proposed formulae can also be applied to the stability of columns having rigid, semi-rigid and simple connections, with or without elastic supports. Semi-rigid connection effects were explicitly included. The end fixity factors were selected to consider the effects of semi-rigid connections in stability analysis, since they were practical and convenient.
The buckling load is obtained by making the determinant of a 4x4 matrix equal to zero for columns having side-sway uninhibited or partially inhibited at both ends, and of a 3x3 matrix for columns having end side-sway inhibited at one or both ends. The effects of lateral bracing one or both ends of the column have been presented. The buckling load of five classical cases was presented and compared to those by other analytical methods to demonstrate the use and relative simplicity of the proposed column classification and corresponding stability equations. Tables 1-5 can be used directly in stability analysis of columns having semirigid connections on an elastic foundation. The proposed method and its equations can be programmed, facilitating calculations and efficient computer coding and avoiding cumbersome procedures. It should be emphasised that the proposed model is just an approximation of the real load transfer mechanism on piles, drilled shafts, caissons and piers. It neglects the soil-pile friction skin contribution to load capacity and is unable to calculate vertical settlement and stresses in foundation soils which are generally the controlling factors during design.
The analytical results indicated that the effects of a uniformly distributed lateral support of magnitude ks became more significant in columns having free ends than in columns having both ends restrained against rotation and side-sway. The buckling load of a column, laterally supported by a very soft elastic foundation, could be substantially increased by either restraining its ends against rotation or by bracing both ends against side-sway.
References
Arboleda-Monsalve, L. G., Zapata-Medina, D. G., Aristizabal-Ochoa, J. D., Timoshenko beam-column with generalized end conditions on elastic foundation: Dynamic-stiffness matrix and load vector., Journal of Sound and Vibration, Vol. 310, 2008, pp. 1057-1079 [ Links ]
Areiza-Hurtado, M., Vega-Posada, C., Aristizabal-Ochoa, J. D., Second-Order Stiffness Matrix and Loading Vector of a Beam-Column with Semirigid Connections on an Elastic Foundation., J. Engrg. Mech., ASCE, Vol. 131, No. 7, 2005, pp. 752-762. [ Links ]
Aristizabal-Ochoa, J. D., K-Factor for Columns in any Type of Construction: Nonparadoxical Approach., J. Struct. Engrg., ASCE, Vol. 120, No. 4, 1994, pp. 1272-1290. [ Links ]
Aristizabal-Ochoa, J. D., Braced, partially braced and un-braced columns: complete set of classical stability equations., Int. J. Struct. Engrg. and Mech., Vol. 4, No. 4, 1996, pp. 365-381. [ Links ]
Aristizabal-Ochoa, J. D., Story stability of braced, partially braced and unbraced frames: classical approach., J. Struct. Engrg., ASCE, Vol. 123, No. 6, 1997, pp. 799-807. [ Links ]
Aristizabal-Ochoa, J. D., Elastic stability of beam-columns with flexural connections under various conservative end axial forces., J. Struct. Engrg., ASCE, Vol. 123, No. 9, 1997, pp. 1194-1200. [ Links ]
Avramidis, I. E., Morfidis, K., Bending of beams on three-parameter elastic foundation., Int. J. Solids Struct., Vol. 43, 2006, pp. 357-375. [ Links ]
Chen, W. F., Lui, E. M., Structural Stability: Theory and Implementation., Englewood, New Jersey, PTR Prentice Hall, 1987, pp. 2. [ Links ]
Cheng, F. Y., Pantelides, C. P., Static Timoshenko Beam-Columns on Elastic Media., J. Struct. Engrg., ASCE, Vol. 114, No. 5, 1988, pp. 1152-1172. [ Links ]
Hetenyi, M., Beams on elastic Foundation., 8th printing, Ann Arbor, Michigan, The University of Michigan Press, 1967, Chapter VII. [ Links ]
Monforton, G. R., Wu, T. S., Matrix analysis of semi-rigidly con-nected frames., J. Struct. Engrg., ASCE, Vol. 89, No. 6, 1963, pp. 13-42. [ Links ]
Morfidis, K., Exact matrices for beams on three-parameter elastic foundation., Computers & Structures, Vol. 85, No. 15-16, 2007, pp. 1243-1256. [ Links ]
Morfidis, K., Vibration of Timoshenko beams on three-parameter elastic foundation., Computers & Structures, Vol. 88, No. 5-6, 2010, pp. 294-308. [ Links ]
Onu, G., Finite Elements on Generalized Elastic Foundation in Timoshenko Beam Theory., J. of Engineering Mechanics-ASCE, Vol. 134, No. 9, 2008, pp. 763-776. [ Links ]
Razaqpur, D. G., Stiffness of beam-columns on elastic foundation with exact shape functions., Computers & Structures, Vol. 24, No. 5, 1986, pp. 813-819. [ Links ]
Struthers, A., Jayaraman, G., Elastic stability of columns on partial elastic foundations under subtangential loading., J. of Sound and Vibration, Vol. 329, No. 18, 2010, pp. 3856-3865. [ Links ]
Scott, R. F., Foundation Analysis., Englewood Cliffts, NJ., Prentice-Hall, 1981. [ Links ]
Timoshenko, S. P., Gere, J. M., Theory of elastic stability., 2nd. Ed., New York, N.Y., McGraw-Hill, 1961, pp. 100-107. [ Links ]
Wang, C-M., Xiang, Y., Kitipornchai, S., Buckling of restrained columns with shear deformation and axial shortening., J. of Engrg. Mech., ASCE, Vol. 117, No. 9, 1991, pp. 1973-1989. [ Links ]
West, H. H., Mafi, M., Eigenvalues for columns on elastic supports., J. Struct. Engrg, ASCE, Vol. 110, No. 6, 1984, pp. 1305-1320. [ Links ]
Zapata-Medina, D. G., Arboleda-Monsalve, L. G., Aristizabal-Ochoa, J. D., Static Stability Formulas of a Weakened Timoshenko Column: Effects of Shear Deformations., J. of Engineering Mechanics-ASCE, Vol. 126, No. 12, 2010, pp. 1-9. [ Links ]













