Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.35 no.1 Bogotá Jan.Apr. 2015
https://doi.org/10.15446/ing.investig.v35n1.44000
DOI: http://dx.doi.org/10.15446/ing.investig.v35n1.44000
J. Gallardo-Alvarado1 and L. Pérez-González2
1 Jaime Gallardo-Alvarado. Doctor en Ciencias en Ingeniería Eléctrica, Instituto Tecnológico de la Laguna, México. Affiliation: Instituto Tecnológico de Celaya, México. E-mail: jaime.gallardo@itcelaya.edu.mx
2 Luciano Pérez-González. Maestro en Ingeniería Mecánica, ITESM, Campus Monterrey, México. Affiliation: Instituto Tecnológico de Celaya, México. E-mail: luciano.perez@itcelaya.edu.mx
How to cite: Gallardo-Alvarado, J., & Pérez-González, L. (2015). Kinematics of an actuating mechanism for a telescoping antenna. Ingeniería e Investigación, 35(1), 5-11. DOI: http://dx.doi.org/10.15446/ing.investig.v35n1.44000
ABSTRACT
In this work the position, velocity and acceleration analyses of a four-degrees-of-freedom serial manipulator are approached mainly by means of the theory of screws. Closed-form solutions are easily obtained for the displacement analysis of the mechanism owing the decoupled action of the generalized coordinates, while the input-output equations of velocity and acceleration of the manipulator are systematically obtained by means of the theory of screws. A case study is included with the purpose to exemplify the application of the method.
Keywords: Serial manipulator, Kinematics, Screw Theory.
RESUMEN
En este trabajo los análisis de posición, velocidad y aceleración de un manipulador serial de cuatro grados de libertad se abordan principalmente por medio de la teoría de tornillos. El análisis de posición es resuelto en forma cerrada debido a la acción desacoplada de las coordenadas generalizadas mientras que las ecuaciones entrada salida de velocidad y aceleración del manipulador son obtenidas sistemáticamente por medio de la teoría de tornillos. Con el propósito de ejemplificar el método se proporciona un caso de estudio.
Palabras clave: Manipulador serial, Cinemática, Teoría de Tornillos.
Received: June 13th 2014 Accepted: October 16th 2014
Introduction
Screw theory is a trusted and confident mathematical resource to address the spatial kinematics of rigid body. In 1830 Chasles introduced the concept of twist motion of a rigid body which was deeply developed by Poinsot while the notion of screw coordinates was introduced by Plücker. Formally, the mathematical framework was developed by Ball (1900) with the purpose to approach the kinematics and statics of rigid body. Two decades later von Mises (1924a, 1924b) published his Motor Calculus where the general equations of motion of rigid body are established based on the so-called motor product. Applications of screw theory concerned mainly with the so-called first-order analysis of rigid body have been widely reported in the literature ranging from projective geometry, screw systems, statics, synthesis, theory of extension and so far. However, the acceleration analysis using exclusively screw theory was unlooked for many years due, perhaps, to the difficulty to express in screw form the accelerator introduced by Brand (1947) and applied by Sugimoto (1989, 1990) in the kinematics of robot manipulators. Thus it is not surprising that for a long time some kinematicians have assumed that screw theory cannot be employed to handle the higher-order kinematics of mechanisms. In fact, by the time it was believed that screw theory will be confined to the first-order analysis of rigid body. It was almost two decades ago when Rico and Duffy (1996) published a remarkable contribution entitled “An application of screw algebra to the acceleration analysis of serial chains” that screw theory was recognized as a viable option to approach the higher-order kinematic analyses of open and closed chains. However, even though the rigorous mathematical procedures employed in such contribution, the material exposed was bitterly disappointed by some kinematicians who claim that screw theory would not be extended to the acceleration analysis.
In this work as a little proof of the potential of screw theory in the analysis of open chains, the infinitesimal kinematics of a four-degrees-of-freedom serial manipulator is investigated by resorting to screw theory. For the sake of completeness, the displacement analysis of the robot is also included. Numerical examples are included in order to show the application of the method.
Preliminary Screw Theory
As a consideration for readers unfamiliar with the theory of screws, this section is devoted to review some elementary concepts of it. In Plücker coordinates a screw, notated as $, is a six-dimensional vector given by $ = (s, s0), where s is named the primal of the screw, P($) = s, and denotes the direction of the line. Usually the primal part is a unit vector of course along the instantaneous screw axis (ISA). While s0 is named the dual part of the screw, D($) = s0, and involves the moment produced by vector around the reference pole 0. The vector s0 is calculated as follows

Therein h is the pitch of the screw while r is a vector directed from an arbitrary point of the ISA to the reference pole 0. Conveniently, the reference pole is chosen as the origin of the reference frame in order to simplify the Plücker coordinates. In a revolute joint the pitch h vanishes yielding $ = (s, s × r), while in a prismatic joint the pitch goes to infinity yielding $ = (0, s). Furthermore, any lower kinematic pair may be modeled combining revolute and/or prismatic joints, e.g. a spherical joint may be modeled as three concurrent revolute joints while a cylindrical joint is modeled as the combination of one prismatic joint with one revolute joint.
The Lie algebra se(3) of the Euclidean group SE(3) is the set of elements of the form $ = (s, s0). Let $1 = (s1, s01), $2 = (s2, s02) and $3 = (s3, s03) be three elements of the Lie algebra se(3). Furthermore, consider that μ1, μ2, μ3 ∈ R. Concerned with the contribution, the Lie algebra supports the following operations
Addition, $1 + $2 = (s1 + s2, s01 + s02)
Multiplication by a scalar, μ$ = (μs, μs0)
Lie product, [$1 $2] = (s1 × s2, s1 × s02 - s2 × s01)
Furthermore, the Lie products has the following properties
Nilpotent, [$1 $1] = 0
Distributive, [$1 μ2$2 + μ3$3] = μ2[$1 $2] + μ3[$1 $3]
[μ1$1 + μ2$2 $3] = μ1[$1 $3] + μ2[$2 $3]
Jacobi identity, [$1[$2 $3]] + [$3[$1 $2]] + [$2[$3 $1]] = 0
The representation of the kinematic states of a rigid body, as observed from another body or reference frame, has been a topic that has attracted the attention of kinematicians since many years ago. In fact, it dates back to the pioneering contribution of Ball (1900). The velocity state, or twist about a screw, of rigid body was defined by Ball (1900) as a six-dimensional vector given by

where ω is the angular velocity vector of the body while v0 is the linear velocity vector of a point 0 embedded to it. Almost four decades after the contribution of Ball, a representation of the acceleration state of rigid body was proposed by Brand (1947) as follows
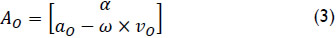
where α denotes the angular acceleration of the vector while a0 denotes the linear acceleration vector of point 0.
It is interesting to note that the primal part of the acceleration state is obtained directly as the time derivative of the primal part of the velocity state, i.e.
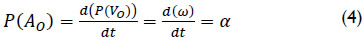
Thus, at this moment a natural question arises, why don’t occur the same for the dual part of the acceleration state? The answer to this query can be found in the heart of the theory of helicoidal vector fields, for details the reader is referred to Gallardo-Alvarado et al (2008).
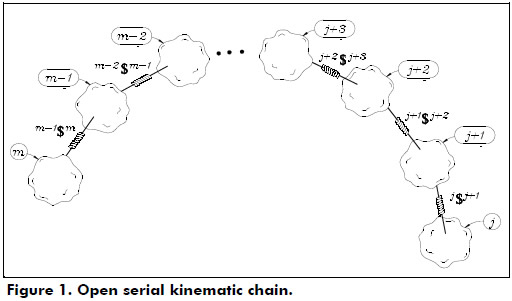
Consider an open kinematic chain as shown in Figure 1, where adjacent bodies are connected by means of infinitesimal screws also known as helical pairs. The velocity state of the end-effector as measured from the base link may be expressed in screw form, see for instance Sugimoto and Duffy (1982), as a linear combination of the involved screws as follows
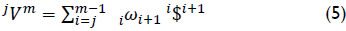
where iωi+1 denotes the ith joint-rate velocity between adjacent bodies i and i+1. By the time, the usefulness of Eq. (5) in robot kinematics was immediately recognized by engineers and scientists; however its extension to the acceleration analysis remained as an open problem for more than one decade. Certainly, the difficulty to express in screw form the acceleration state of kinematic chains was considered as one of the main drawbacks of the theory of screws. It was in 1996 when Rico and Duffy (1996) introduced the following equation
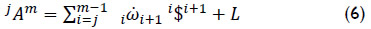
where 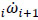 denotes the ith joint-rate acceleration between adjacent bodies, i.e.
denotes the ith joint-rate acceleration between adjacent bodies, i.e. 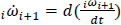 , while L was named the Lie screw of acceleration and it is calculated according to the joint-rate velocities of the serial chain as follows
, while L was named the Lie screw of acceleration and it is calculated according to the joint-rate velocities of the serial chain as follows
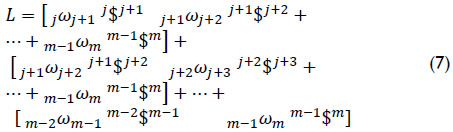
For clarity, unlike the equation of velocity state in screw-form, in the contribution the six-dimensional vector L is written explicitly. Equation (6) was named by Rico and Duffy (1996) as the reduced acceleration state. After the publication of that theoretical paper, screw theory was recognized, unfortunately only by a reduced number of kinematicians, as a viable option to approach not only the acceleration analysis but also the jerk analysis (Rico et al, 1999) and the hyper-jerk analysis of robot manipulators (Gallardo-Alvarado, 2014). Equation (7) has been proved successfully in a wide variety of parallel manipulators. The relevant results of such analyses were reported in several indexed journals by the author of this contribution, see for instance Gallardo-Alvarado et al (2011), Gallardo-Alvarado (2012), Gallardo-Alvarado and García-Murillo (2013). In this occasion in order to show the viability of the theory of screws in the kinematic analysis of robot manipulators, a four-degrees-of-freedom open kinematic chain is chosen as the robot under study.
Description of the Mechanism
The topology of the robot manipulator under study, and its geometric scheme, is outlined in Figure 2.
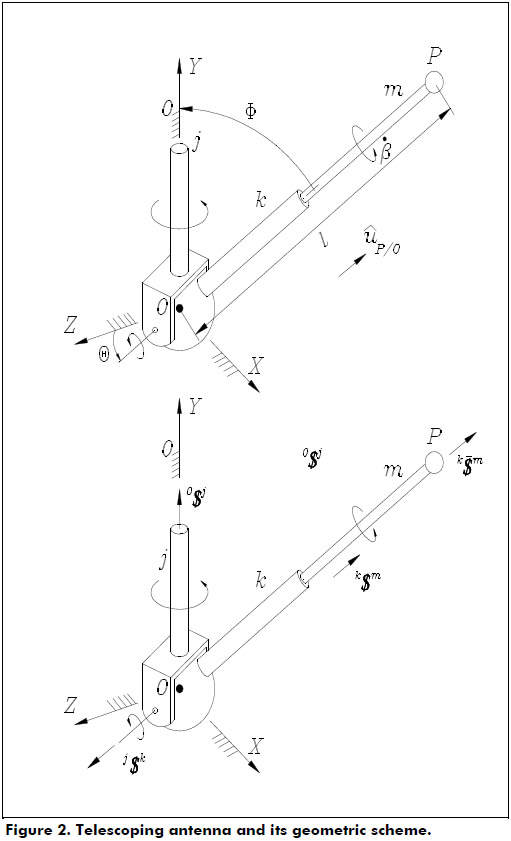
The spatial mechanism is composed of an extendible limb l formed with two bodies labeled k and m connected by means of a cylindrical joint where the translation of body m with respect to body k is represented by means of the screw 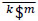 while the rotation between the same bodies is represented by means of the screw k$m. Furthermore, the orientation of the limb is controlled through the angles Ø and θ. On the other hand, in order to improve the performance of the original telescoping antenna, an additional freedom was added to the mechanism through the rotational angle β between bodies m and k. In other words the prismatic joint of the original mechanism was replaced with a cylindrical joint. The generalized coordinate β is added to the manipulator with the purpose to increase the mobility of a possibly body attached to body m, e.g. a gripper.
while the rotation between the same bodies is represented by means of the screw k$m. Furthermore, the orientation of the limb is controlled through the angles Ø and θ. On the other hand, in order to improve the performance of the original telescoping antenna, an additional freedom was added to the mechanism through the rotational angle β between bodies m and k. In other words the prismatic joint of the original mechanism was replaced with a cylindrical joint. The generalized coordinate β is added to the manipulator with the purpose to increase the mobility of a possibly body attached to body m, e.g. a gripper.
Displacement Analysis
Let XYZ be a reference frame with associated unit vectors 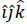 . Furthermore, let be the control point of the manipulator.
. Furthermore, let be the control point of the manipulator.
The inverse displacement analysis is formulated as follows. Given the coordinates of point P it is required to determine the orientating angles θ and Ø, and the length l of the antenna. The length l is directly computed as
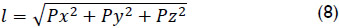
After, the angle Ø is obtained in the range (0,π) as
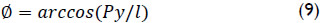
In order to find the angle θ consider that the revolute joint connecting bodies j and k constraints the position of point P in such a way that

Where 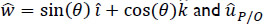 is a unit vector pointed from 0 to P while the dot (·) denotes the dot product of usual three-dimensional vectorial algebra. Thus it follows that the angle θ must satisfy the relationship tan(- θ) = Pz/Px. Hence in terms of the standard arctan function, whose range is
is a unit vector pointed from 0 to P while the dot (·) denotes the dot product of usual three-dimensional vectorial algebra. Thus it follows that the angle θ must satisfy the relationship tan(- θ) = Pz/Px. Hence in terms of the standard arctan function, whose range is 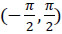 , the angle θ is obtained as
, the angle θ is obtained as
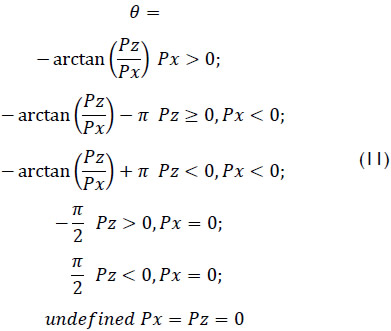
On the other hand, the forward displacement analysis consists of finding the coordinates of point P given the generalized coordinates Ø, θ and l. This analysis is straightforward. Indeed
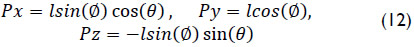
According to Eq. (12) it is possible to conclude that there are coupled motions of the generalized coordinates l, Ø and θ in order to obtain a specific position for point P.
Velocity Analysis of the Serial Manipulator
Let 0ωm be the angular velocity vector of the end-effector m as measured from the base link 0 and let v0 be the velocity of a point of the body m which is instantaneously coincident with the origin of the reference frame XYZ. According to Eq. (5) the velocity state of body as measured from body m, the vector 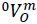 , is given in screw form as follows
, is given in screw form as follows
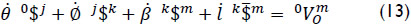
Where, taking into account that point 0 is chosen as the reference pole, in Plücker coordinates the infinitesimal screws of the robot are computed as
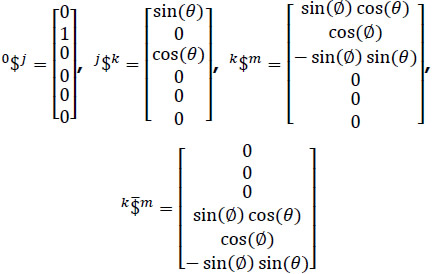
On the other hand, in order to satisfy the rank of the Jacobian matrix spanned by the infinitesimal screws two virtual, or imaginary, prismatic joints, along the X and Z axes passing through point 0, are added to the serial manipulator. Hence Eq. (13) becomes into
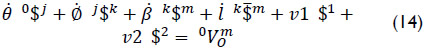
Where v1 = v2 = 0 provided that these joint-rates are associated to virtual prismatic pairs. The screws $1 and $2 are given in Plücker coordinates as follows
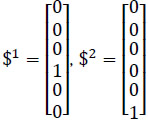
After, Eq. (14) may be rewritten in a compact form as follows

Where 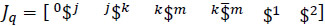 is called the screw-coordinate Jacobian matrix of the manipulator while Jx is the identity matrix of order 6. Furthermore vector
is called the screw-coordinate Jacobian matrix of the manipulator while Jx is the identity matrix of order 6. Furthermore vector 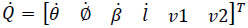 is named the first-order driver of the robot. Equation (15) is called the input-output equation of velocity of the manipulator.
is named the first-order driver of the robot. Equation (15) is called the input-output equation of velocity of the manipulator.
The forward velocity analysis consists of finding the velocity state 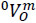 given a set of generalized speeds
given a set of generalized speeds 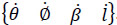 . It is evident that this analysis is free of singularities since det(Jx) for any posture of the mechanism. On the other hand, the inverse velocity analysis of the manipulator consists of finding the generalized speeds given the six-dimensional vector
. It is evident that this analysis is free of singularities since det(Jx) for any posture of the mechanism. On the other hand, the inverse velocity analysis of the manipulator consists of finding the generalized speeds given the six-dimensional vector 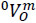 . Unlike, the forward velocity analysis, the inverse velocity analysis is not free of singular configurations. In fact, taking into account that det(Jq) = -sin(Ø)cos(Ø), the manipulator falls into a singularity when sin(Ø)cos(Ø) = 0, e.g. when Ø = 0 or Ø = π/2. It is worth to note that the generalized coordinate θ is not responsible to fall-escape the manipulator from singular postures, if the manipulator confirms, as concluded by Waldron et al (1985), that in a serial manipulator the kinematic pair connecting the open chain to the base link is not responsible of the feasible singularities of the serial manipulator. On the other hand, it is evident that the manipulator at hand cannot perform arbitrary velocity states owing the loss freedoms of it, consider for instance that the coordinates Px and Pz are related through Eq. (10). Finally, according to Eq. (13) the angular velocity 0ωm results in
. Unlike, the forward velocity analysis, the inverse velocity analysis is not free of singular configurations. In fact, taking into account that det(Jq) = -sin(Ø)cos(Ø), the manipulator falls into a singularity when sin(Ø)cos(Ø) = 0, e.g. when Ø = 0 or Ø = π/2. It is worth to note that the generalized coordinate θ is not responsible to fall-escape the manipulator from singular postures, if the manipulator confirms, as concluded by Waldron et al (1985), that in a serial manipulator the kinematic pair connecting the open chain to the base link is not responsible of the feasible singularities of the serial manipulator. On the other hand, it is evident that the manipulator at hand cannot perform arbitrary velocity states owing the loss freedoms of it, consider for instance that the coordinates Px and Pz are related through Eq. (10). Finally, according to Eq. (13) the angular velocity 0ωm results in
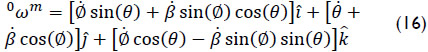
While the velocity vector 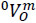 is obtained as
is obtained as
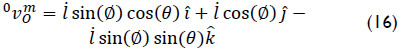
Furthermore, using elementary kinematics the velocity of point P is computed as
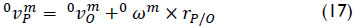
where rP/0 is a vector pointed from point 0 to point P. Hence one obtains
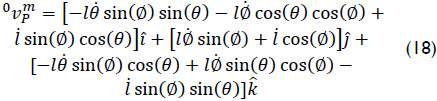
Equations (17) and (18) indicate that given the velocity state of the end-effector, taking point P as the reference pole, there are six equations available to compute the four generalized speeds of the robot. The limitations of mobility of the manipulator are evident owing the dependency between such equations. In fact the end-effector of the robot cannot undergo arbitrary velocity states. For example, concerned with the velocity of point P the architecture of the manipulator is such, see Eq. (10), that 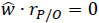 . Hence upon the time derivative of such constraint it follows that Eq. (18) is restricted to satisfy the expression vxcosθ = vzsinθ. The available motions of the antenna may be easily explained if one consider that the orientation of the antenna is controlled by means of the three independent angles θ, Ø and β and therefore the knob can adopt arbitrary orientations as observed from the base link while, according to the limitations of the manipulator, only one translation of point P can be selected freely.
. Hence upon the time derivative of such constraint it follows that Eq. (18) is restricted to satisfy the expression vxcosθ = vzsinθ. The available motions of the antenna may be easily explained if one consider that the orientation of the antenna is controlled by means of the three independent angles θ, Ø and β and therefore the knob can adopt arbitrary orientations as observed from the base link while, according to the limitations of the manipulator, only one translation of point P can be selected freely.
Acceleration Analysis of the Serial Manipulator
Let 0αm be the angular acceleration vector of the end-effector m as measured from the base link 0 and let 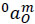 be the acceleration of a point of the body m which is instantaneously coincident with the origin of the reference frame XYZ. According to Eq. (6), the reduced acceleration state of body m as measured from body 0, the vector
be the acceleration of a point of the body m which is instantaneously coincident with the origin of the reference frame XYZ. According to Eq. (6), the reduced acceleration state of body m as measured from body 0, the vector 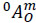 , is given in screw form as follows
, is given in screw form as follows
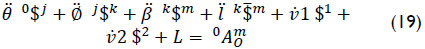
Where the Lie screw of acceleration, see Eq. (7), is given by
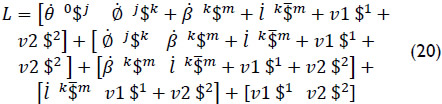
Furthermore, due to the fact that the joint-rate velocities v1 and v2 vanish, then the Lie screw of acceleration is reduced to
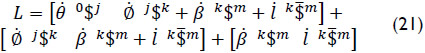
After, the input-output equation of acceleration of the manipulator may be re-written, see Eq. (19), as follows

where 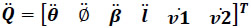 is called the second-order driver matrix of the manipulator. Evidently it follows that
is called the second-order driver matrix of the manipulator. Evidently it follows that 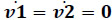 owing that these joint-rate accelerations are associated to fictitious kinematic pairs.
owing that these joint-rate accelerations are associated to fictitious kinematic pairs.
Once the velocity analysis of the manipulator was solved, the forward acceleration analysis of the kinematic chain consists of finding the reduced acceleration state 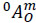 given a set of generalized accelerations
given a set of generalized accelerations 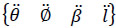 . On the other hand, the inverse acceleration analysis consists of finding the generalized accelerations given the six-dimensional vector
. On the other hand, the inverse acceleration analysis consists of finding the generalized accelerations given the six-dimensional vector 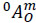 . Both analyses may be solved by means of Eq. (22). Furthermore, after a few computations, the primal part of the reduced acceleration state
. Both analyses may be solved by means of Eq. (22). Furthermore, after a few computations, the primal part of the reduced acceleration state 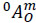 is obtained as
is obtained as
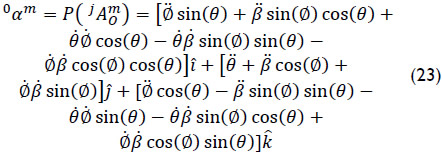
while the corresponding dual part of the six-dimensional vector 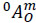 is obtained as
is obtained as
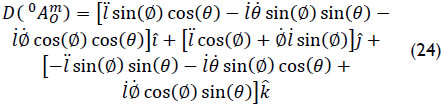
Thus according to Eq. (3), the acceleration of point 0 fixed in body m as observed from the base link 0 is given by
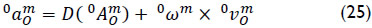
Finally, using elementary kinematics the acceleration of point P, fixed in body as observed from body m, is calculated as
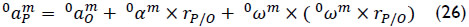
Numerical Example
In order to show the application of the method, in this section a case study is reported.
The first part of the example is devoted to the forward kinematics of the mechanism. To this end, using thorough the numerical example SI units, consider that in the reference configuration the generalized coordinates of the manipulator are given by θ = π/9, Ø = π/10, l = 0.75m. Furthermore, consider that upon the home position of the manipulator we have a constant angular velocity 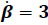 while the generalized coordinates of the manipulator are commanded to follow periodical functions given by
while the generalized coordinates of the manipulator are commanded to follow periodical functions given by
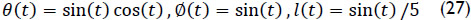
where the time t is confined to the interval 0 < t < 2π. Thus in the home position of the robot when t = 0, the coordinates of point P are obtained as P = (0.217,0.713,-0.079). With these data it is required to determine the temporal behavior of point P. The involved equations in the solution of the forward position, velocity and acceleration analyses were translated into a Maple12 sheet. The relevant plots thus obtained are provided in Figure 3.
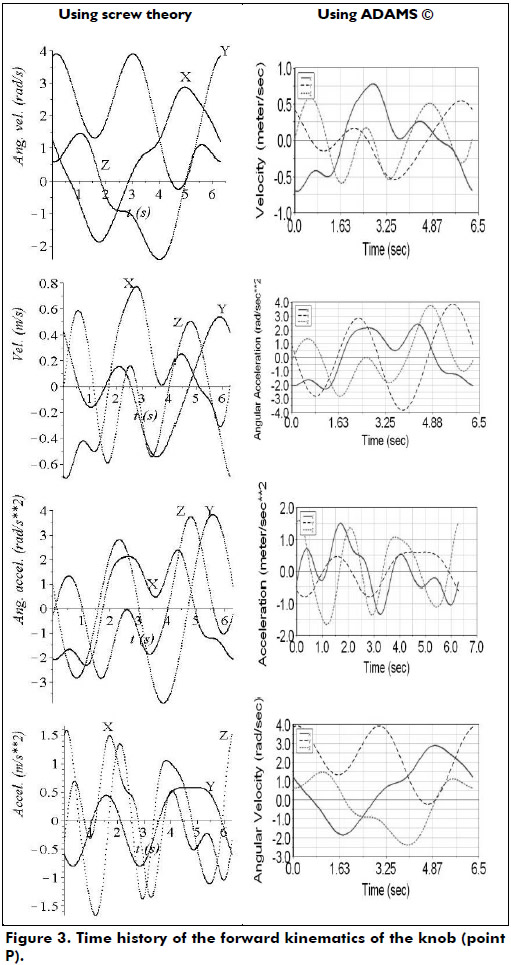
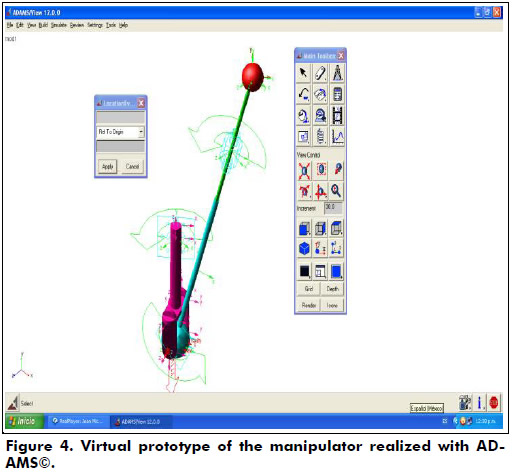
Furthermore, in order to verify the numerical results obtained via screw theory, the forward kinematics of the numerical example was carried-out by means of a different approach such is the application of commercially available software like ADAMS©. For a rapid comparison between both strategies the plots generated with ADAMS© were added to Figure 3. The virtual prototype is shown in Figure 4.
The next part of the exercise is dedicated to the inverse kinematics of the manipulator. To this end, it must be taken into proper account that the manipulator at hand is a limited-dof serial manipulator, i.e. the vectors contained in the velocity state are dependent vectors each other. Thus, it is necessary to select properly the task assigned to the end-effector. One feasible selection is to assume that point P can adopt arbitrary positions with respect to the base link. With these assumptions in mind it is desired that upon the home position of the antenna, i.e. when P = (0.217,0.713,-0.079), point P = (Px,Py,Pz) is commanded to follow periodical functions given by
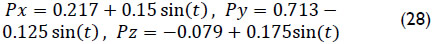
keeping a constant orientation of body m with respect to body k, e.g. 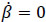 . With these data it is required to compute the generalized coordinates, and their time derivatives, that allow the manipulator to perform the assigned task.
. With these data it is required to compute the generalized coordinates, and their time derivatives, that allow the manipulator to perform the assigned task.
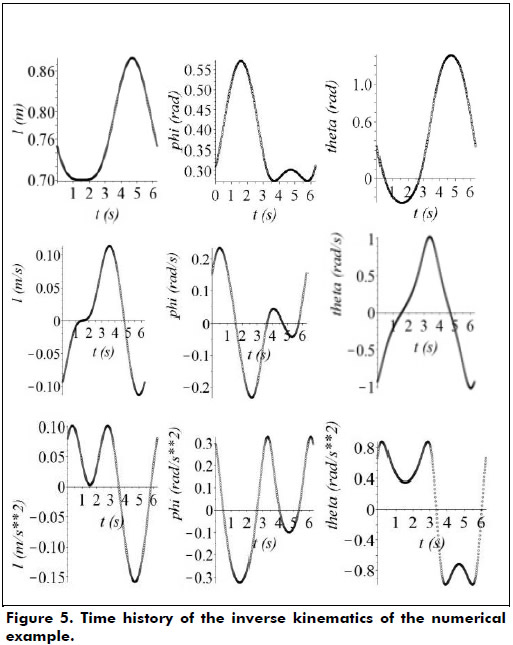
The extendible length l is computed directly from Eq. (8) while the angles Ø and θ are calculated, respectively, by means of Eqs. (9) and (11). Furthermore, the generalized speeds and accelerations are obtained based on the first and second time derivatives of Eqs. (28). Figure 5 shows the plots of the obtained simulations.
In order to exemplify the mobility limitations of the manipulator concerned with the virtual prototype realized with ADAMS© the following trajectories were imposed to point P of the knob: three rotations +Px, three rotations +Py, three rotations +Pz. All the imposed trajectories were successfully performed by the manipulator. However, when additional conditions were assigned to point P, e.g. three rotations+PX +PY, the simulations with ADAMS© fail invariably.
Conclusions
“Unfortunately, screw theory is usually explained following descriptive definitions rather than short axiomatic lines of reasoning”, Minguzzi (2013).
“Screw theory allows simple geometrical interpretation, but it is restricted to speed and infinitesimal displacement analysis”, Legnani et al (1996).
Comments like the above given can be found in the specialized literature. In this work, the kinematics of a four-degrees-of-freedom serial manipulator employed as an actuating mechanism for a telescoping antenna is investigated by means of the theory of screws. Simple equations in closure form are easily obtained to solve the displacement analysis of the manipulator. After, the input-output equations of velocity and acceleration are systematically obtained by resorting to the theory of screws. Numerical examples, which were successfully verified with the aid of special software like ADAMS©, are provided in order to show the application of the method. This work is a proof that screw theory is not an “old-fashioned” mathematical resource confined to the so-called first-order kinematics of rigid body.
References
Ball, R. S. (1900). The Theory of Screws. Cambridge University Press. [ Links ]
Brand, L. (1947). Vector and Tensor Analysis. John Wiley & Sons. [ Links ]
Rico, J. M., & Duffy, J. (1996). An application of screw algebra to the acceleration analysis of serial chains. Mechanism and Machine Theory, 31(4), 445-457. [ Links ]
Rico, J. M., Duffy, J., & Gallardo, J. (1999). Screw theory and higher order kinematic analysis of open serial and closed chains. Mechanism and Machine Theory, 34(4), 559-586. [ Links ]
Gallardo-Alvarado, J. (2012). Jerk analysis of a six-degrees-of-freedom three-legged parallel manipulator. Robotics and Computer-Integrated Manufacturing, 28, 220-226. [ Links ]
Gallardo-Alvarado, J. (2014). Hyper-jerk analysis of robot manipulators. Journal of Intelligent and Robotic Systems, 74(3-4), 625-641. [ Links ]
Gallardo-Alvarado, J., & García-Murillo, M. A. (2013). A parallel manipulator inspired by the original Stewart platform. Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 227(4), 831-844. [ Links ]
Gallardo, J., Lesso, R., Rico, J. M., & Alici, G. (2011). The kinematics of modular spatial hyper-redundant manipulators formed from RPS-type limbs. Robotics and Autonomous Systems, 59(1), 12-21. [ Links ]
Gallardo-Alvarado, J., Mendoza-Orozco, H., & Rodríguez-Castro, R. (2008). Finding the jerk properties of multibody systems using helicoidal vector fields. Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 222(11), 2217-2229. [ Links ]
Legnani, G., Casolo, F., Righettini, P., & Zappa, B. (1996). A homogeneous matrix approach to 3D kinematics and dynamics-I. Theory, Mechanism and Machine Theory, 31(5), 573-587. [ Links ]
Minguzzi, E. (2013). A geometrical introduction to screw theory. European Journal of Physics, 34, 613-622. [ Links ]
Sugimoto, K. (1989). Computational scheme for dynamic analysis of parallel manipulators. ASME Journal of Mechanisms, Transmissions, and Automation in Design, 111, 29-33. [ Links ]
Sugimoto, K. (1990). Existencia criteria for overconstrained mechanisms. An extension of motor algebra. ASME Journal of Mechanical Design, 112(3), 295-298. [ Links ]
Sugimoto, K., & Duffy, J. (1982). Application of linear algebra to screw systems. Mechanism and Machine Theory, 17(1), 73-83. [ Links ]
Von Mises, R. (1924). Motorrechnung, ein neues hilfsmittel der mechanic. Zeitschrift für Angewandte Mathematik und Mechanik, 4(2), 155-181. [ Links ]
Von Mises, R. (1924). Anwendungen der motorrenchung. Zeitschrift für Angewandte Mathematik und Mechanik, 4(3), 193-213. [ Links ]
Waldron, K. J., Wang, S. L., & Bolin, S. J. (1985). A study of the Jacobian matrix of serial manipulators. ASME Journal of Mechanisms, Transmissions, and Automation in Design, 107(2), 230-238. [ Links ]













