Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.35 no.1 Bogotá Jan.Apr. 2015
https://doi.org/10.15446/ing.investig.v35n1.45310
DOI: http://dx.doi.org/10.15446/ing.investig.v35n1.45310
C. A. Criollo1 and A. Ávila2
1Carlos Criollo Paredes. Electronic Engineer, Universidad de Nariño, Colombia. M. Sc. in Micro-electronics, Universidad de los Andes, Colombia. Affiliation: Research assistant in Microelectronics Research Center (CMUA), Universidad de los Andes, Colombia. E-mail: ca.criollo99@uniandes.edu.co
2Alba Ávila. Ph. D. in Physics, Cambridge University, United Kingdom. Masters in Microelectronics, Physicist and Electronic Engineer, Universidad de los Andes, Colombia. Affiliation: Associated Professor, Universidad de los Andes, Colombia. E-mail: a-avila@uniandes.edu.co
How to cite: Criollo, C., & Ávila, A. (2015). Simulation of photoconductive antennas for terahertz radiation. Ingeniería e Investigación, 35(1), 60-64. DOI: http://dx.doi.org/10.15446/ing.investig.v35n1.45310
ABSTRACT
Simulation of terahertz (THz) emission based on PC antennas imposes a challenge to couple the semiconductor carrier phenomena, optical transport and the THz energy transport. In this paper a Multi-physics simulation for coupling these phenomena using COMSOL Multi-physics 4.3b is introduced. The main parameters of THz photoconductive (PC) antenna as THz emitter have been reviewed and discussed. The results indicate the role of each parameter in the resulting photocurrent waveform and THz frequency: The radiated THz photocurrent waveform is determined by the photoconductive gap (the separation between the metallic electrodes), the incident laser illumination and the DC excitation voltage; while the THz frequency depends on the dipole length. The optimization of these parameters could enhance the emission. The simulations extend the advance of compact and cost-effective THz emitters.
Keywords: Multi-physics simulation, photoconductive antennas, semiconductor physics, electromagnetics.
RESUMEN
La emisión de Terahertz (THz) empleando antenas fotoconductoras representa un reto de simulación en la integración de los fenómenos de transporte en semiconductores, de óptica y de transporte de energía por radiación THz. En el presente artículo se propone una simulación Multi-Física para integrar estos fenómenos utilizando COMSOL Multiphysics 4.3b. Los principales parámetros de las antenas fotoconductoras empleadas como emisores de THz son estudiados. Los resultados de la simulación demuestran cómo estos parámetros inciden en la fotocorriente generada y en la frecuencia de radiación THz: la abertura fotoconductora (la separación de los electrodos metálicos de la antena), la potencia promedio del láser incidente y el voltaje de polarización, determinan la forma de onda de la fotocorriente generada; mientras que la longitud del dipolo determina la frecuencia de radiación. La emisión de las antenas fotoconductoras puede mejorarse optimizando estos parámetros. Esta simulación es útil para el diseño e implementación de antenas fotoconductoras como emisores de THz de diseño compacto y bajo costo.
Palabras clave: Antena fotoconductora, simulación multi-física, electromagnetismo, física de semiconductores.
Received: August 30th 2014 Accepted: February 11th 2015
Introduction
Material responses to Terahertz radiation (THz) has opened up a large range of industrial applications (Tonouchi, 2007). The THz radiation is located between the infrared and the microwaves electromagnetic spectrum (Lee, 2009). In this range of frequencies the radiation can be described in the infrared by the particle like characteristics and wave-like characteristics in the microwave. THz applications explore the unique properties of THz radiation-matter interaction: Water is highly absorptive, metals are highly reflective and nonpolar and nonmetallic materials such as paper, plastics, wood and textiles are transparent at THz frequencies. These properties have boosted the potential industrial applications of a radiation that is nonionizing, nondestructive, and noninvasive: sensitive liquid spectroscopy (Mickan, Shvartsman, Munch, Zhang, & Abbott, 2004) ultrafast time domain spectroscopy (Tang et al., 2014), explosive detectors for remote sensing (Federici et al., 2005) and bio-imaging with nanometer resolution (150nm)(Chen, Kersting, & Cho, 2003). With these applications panorama the interest in developing compact and cost-effective THz generation and detection techniques has arisen (Berry, Hashemi, & Jarrahi, 2014; Tani et al., 2013).
THz waves generation has been achieved by solid state and optical methods. The former is limited by the generation at cryogenic temperatures (Kumar, Chan, Hu, & Reno, 2011) while the latter has been attained at room temperatures (Khiabani, Huang, Shen, & Boyes, 2011). Optical generation can be further subdivided into optical rectification and photoconductive generation. While optical rectification is well suited to generate intense THz pulses with amplified laser systems, photoconductive emission is much more efficient when standard laser oscillator systems are used (Löffler et al., 2005). Effective THz generation has been reported with photoconductive (PC) antennas with a dipole structure (Venkatesh, Rao, Abhilash, Tewari, & Chaudhary, 2014), with the advantage that it can be patterned on the same semiconductor substrate used for THz detection. A PC antenna consists of two metal planar electrodes deposited on a semiconductor substrate. An optical beam illuminating the gap between the electrodes generates photo-carriers that are accelerated by static bias field to produce a time-varying current that radiates THz electromagnetic waves.
Simulation of THz generation based on PC antennas imposes a challenge to couple the semiconductor carrier phenomena, optical transport and the THz energy transport (Armstrong, 2012). Analytical equations can be applied to describe the most important properties of photoconductive antennas (Lloyd-Hughes, Castro-Camus, & Johnston, 2005), but often losses are neglected, this approach is simple to predict quantitative predictions. On the other hand, in-depth Monte-Carlo simulations describes in great detail the carrier dynamics in a photoconductive antenna (Castro-Camus, Lloyd-Hughes, & Johnston, 2005), however, without focus on effects related to antenna geometry. In the present work a multi-physics simulation for coupling these phenomena is introduced using COMSOL Multiphysics®. Results indicate that the radiated THz waveform is determined by the photoconductive gap (the separation between the metallic electrodes), the incident laser illumination and the DC excitation voltage. The emission intensity of the THz pulse depends on the dipole length. The simulation results are useful for designing THz antennas and tuning the excitation parameters for improved working of these devices.
Generation of THz radiation with PC antennas
Figure 1 shows the schematic diagram of the PC antenna when it is employed as a THz emitter. This generation technique consists of a femtosecond (fs) laser and a micro-striped antenna on a photoconductive material under a DC bias voltage (V). The antenna includes two planar metal electrodes deposited on a semiconductor substrate (i.e SI-GaAs) forming a dipole structure. After laser radiation on the PC gap, electron-hole pairs are accelerated in the biased semiconductor generating an ultra-short photo-current pulse (J(t)) that decreases with a time constant determined by the carrier lifetime in the substrate. Several photoconductive materials have been tested for photoconductive antennas, such as SI-GaAs and LT-GaAs. The advantage of SI-GaAs over LT-GaAs has been demonstrated in antennas in which the saturation effects due to field screening can be avoided (Liu, Tani, & Pan, 2003; Tani, Matsuura, Sakai, & Nakashima, 1997). Typical lifetimes are several hundred picoseconds for SI-GaAs (Tani et al., 1997) and subpicoseconds for LT-GaAs (Gupta, Whitaker, & Mourou, 1992; Tani et al., 1994), respectively. The photo-current is directly dependent on the density of generated photo-carriers N(t), the mobility of electrons µ and the static bias field between the electrodes Eb. It can be expressed by J(t) = N(t) eμEb, where e is the electron charge (Khiabani et al., 2011). The transient current at the PC gap of the antenna radiates an electromagnetic pulse in the THz frequency.
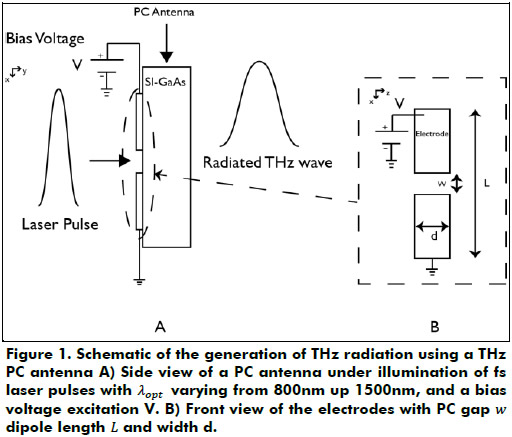
Multi-physics simulation of PC Antenna
The “Electromagnetic Waves, Frequency Domain” interface of the “Wave optics Module” of COMSOL Multiphysics® 4.3b was used for the simulation of the PC antenna as a THz emitter. The complete structure is presented in Figure 2. It consists of three domains: air, gold microelectrodes and a 350µm SI-GaAs substrate with a resistivity of 3.5x107 Ω-cm. These values are taken from commonly used materials in fabrication of PC antennas (Criollo, Avila, & Winnerl, 2014; Shi, Hou, & Wang, 2011).
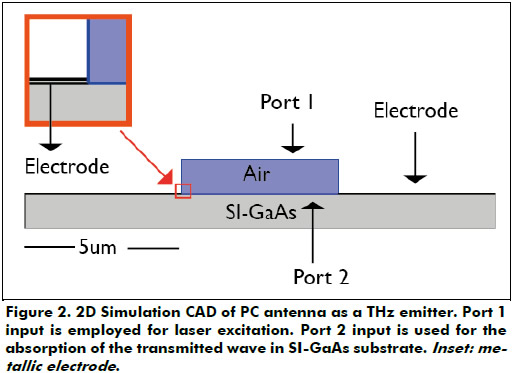
Port node 1 input was used to launch the fs laser excitation with the propagation constant of the air (Hoffmann, Leuchtmann, Ruefenacht, & Hafner, 2009). The fs laser is modeled as a Gauss beam propagating along the z axis with an electric field distribu-tion described by (Saleh & Teich, 1991):
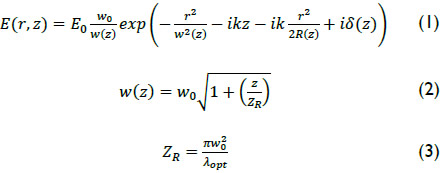
Where 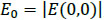 r is the radial distance from the center axis of the beam, w(z) is the variation of the spot radius along the propagation axis, w0 is the minimum value of the spot radius w(z) along the beam axis located at z = 0, called beam waist, ZR is the Rayleigh range, R(z) is the radius of curvature of the beam’s wave fronts and δ(z) is the Gouy phase shift, an extra contribution in the phase that is seen in Gaussian beams (Feng* & Winful, 2001).
r is the radial distance from the center axis of the beam, w(z) is the variation of the spot radius along the propagation axis, w0 is the minimum value of the spot radius w(z) along the beam axis located at z = 0, called beam waist, ZR is the Rayleigh range, R(z) is the radius of curvature of the beam’s wave fronts and δ(z) is the Gouy phase shift, an extra contribution in the phase that is seen in Gaussian beams (Feng* & Winful, 2001).
Port 2 input was used to absorb the transmitted Gaussian beam with the propagation constant of the SI-GaAs substrate (Chazan, Haelterman, & Tedjini, 1992), a wavelength of 800nm, a laser repetition rate of 80MHz, an average output power of 80mW, a pulse width of 15fs and a spot radius of 5µm. The above-mentioned excitation parameters are commonly used in previously published works (Khiabani et al., 2011). Floquet periodic boundary conditions were implemented to limit the simulation to a single periodic element (Zhengqing Yun, 2000). The electric field E(r,z) was employed as an input parameter to the ports and to the Floquet periodic boundary conditions. Free tetrahedral mesh was applied to all the domains with a “fine” resolution of 10nm. This mesh was set smaller than the incident wavelength to resolve the impact of the incident optical power on the PC gap. For the photo-carrier generation simulation in the SI-GaAs substrate under laser excitation, the quasi-analytical model of Duvillaret for PC antennas was employed (Duvillaret, Garet, Roux, & Coutaz, 2001). The calculations in this model are based on the Drude-Lorentz theory to simulate the dynamics of photo-generated free carriers inside the photoconductor and entail a direct proportionality between the time derivative emitter photocurrent 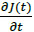 and the emitted THz field ETHZ.
and the emitted THz field ETHZ.
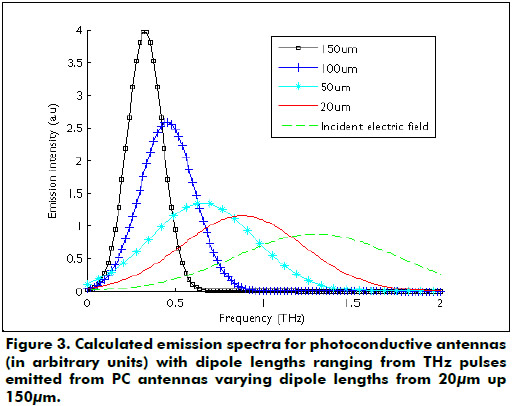
The dependence of the THz emission spectra on the dipole length was investigated. Figure 3 shows the calculated THz emission spectra for PC antennas with dipole length from 20µm to 150µm. The peak field amplitude of the THz transients emitted significantly increases as the dipole length increases. The emitted electric field ETHZ which is proportional to the time derivation of the current J(t) at the gap is calculated using the finite-difference time domain method. It can be seen in Figure 3 that the peak frequency of the THz transients shifts to lower frequency if the dipole length increases. This can be explained by the relationship between the geometrical parameters of the dipole antenna and the spectral shape of the input electric field that determines the characteristics of the THz emitted wave. Having into account that the input electric field (femtosecond laser) changes relatively slowly, the maximum emission intensity can be obtained using a longer dipole length which has a resonance at a lower frequency.
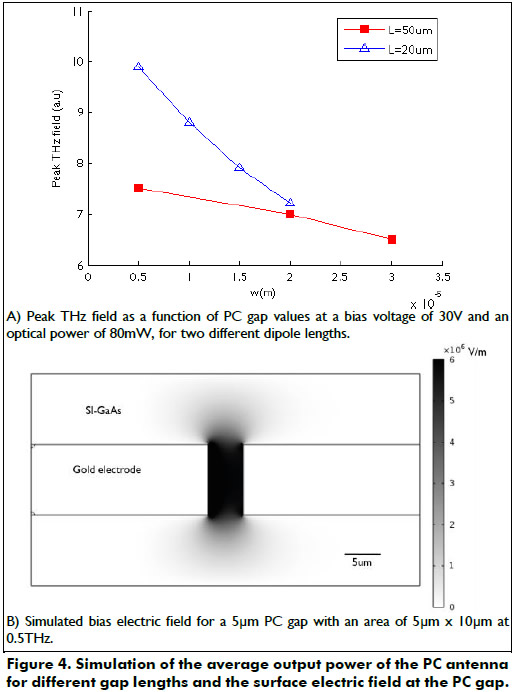
To study the effects of dipole length and gap distance on the peak THz field, PC antennas with gaps varying 5µm up 30µm was simulated. The results of this analysis are presented in Figure 4a. The radiated peak THz field from a PC antenna with a smaller gap increases because of the better overlapping of the laser spot and the region of the high electric field in the PC gap. Moreover, the increment of the electric bias field due to a reduction of the PC gap accelerates a larger concentration of photo-carriers, for example: for a PC gap of 5µm, the field goes up to 6MV/m, see Figure 4b. The slope of this dependence changes with the dipole length.
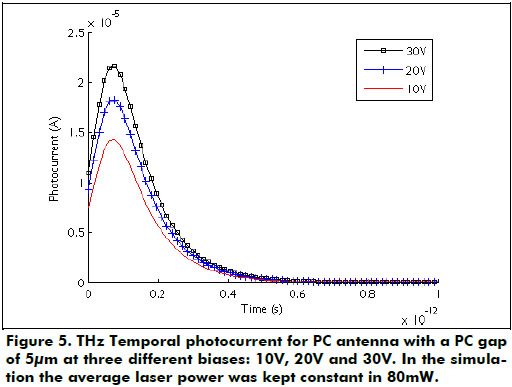
The voltage bias dependence of the generated photocurrent in the PC antenna with 5µm gap length is presented in Figure 5. For higher bias fields, the photo-current pulse shape displays an increase due to the increment in the concentration of accelerated photo-carriers. A current difference of 10.2µA is estimated between the photocurrent peaks of 10V and 30V bias. In these experimental observations, the timescale of the photocurrent peak is associated to the carrier acceleration in the external bias field followed by the transfer from the high mobility r-valley to the low mobility L-valley and hence a stronger deceleration which results in a photocurrent overshoot. The intervalley scattering effect is expected to be more significant in materials with hundred of picosecond carrier life times since the photo carriers would be enough time to be scattered into the L-valley (Liu et al., 2003; Ludwig & Kuhl, 1996).
Another important parameter in the design of PC antennas is the influence of the average laser power on the waveform and the peak current of the generated photo-current, see Figure 6. The laser power was varied from 10mW to 80mW, these values are the reference power from lasers Commercially Available (Spence & Sibbett, 1991).
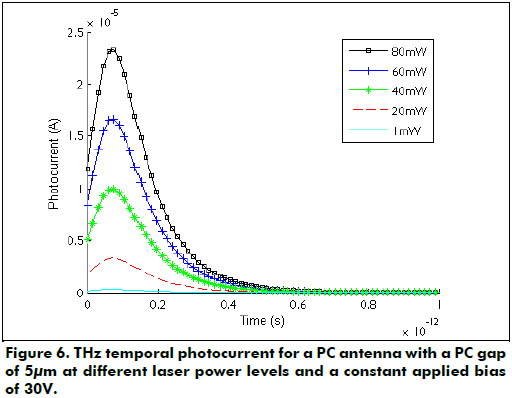
From Figure 6 it can be noted that there is an amplitude increment in the THz pulse shape at higher excitation densities due to an increment in the density of photo-carriers at the PC gap. The saturation behavior reported in experimental works (Loata, Thomson, Löffler, & Roskos, 2007; Tani et al., 1997), that is presented at high fluences of photo-generated carriers in photoconductive antennas is not evident in the Figure 6 because screening effects are not included in the simulation, therefore the results are valid only for low laser power levels. The smallest optical power level at which the PC antenna generates a pulse of photocurrent is below 20mW, where the peak current of the pulse shape is reduced at 0.09µA.
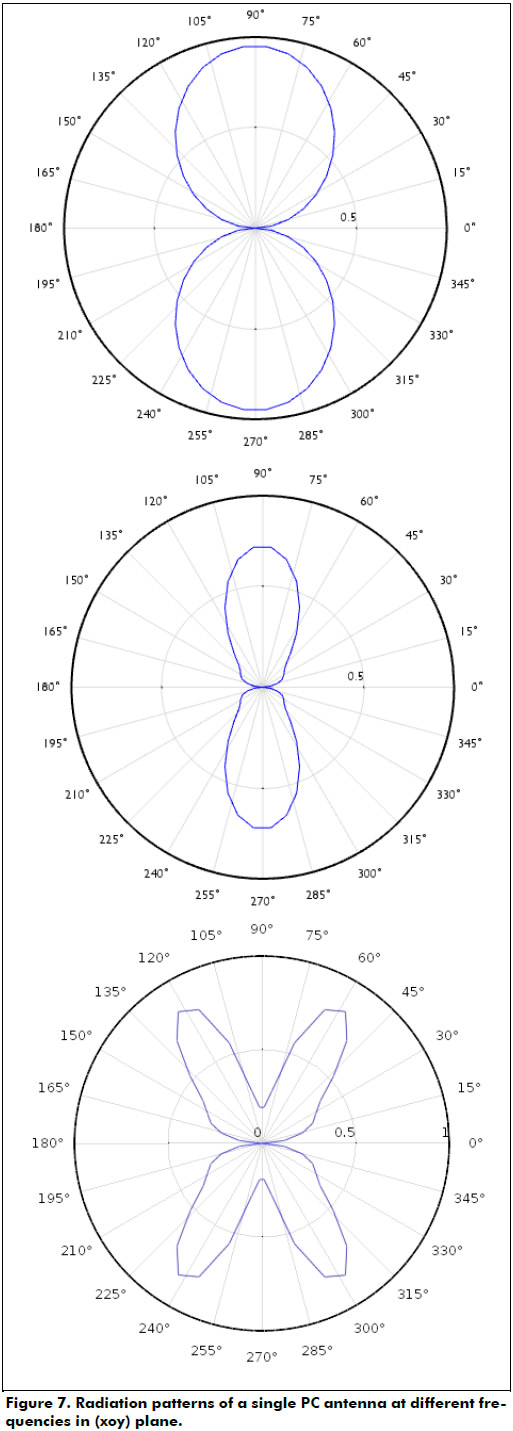
The radiation patterns of the simulated PC Antenna with a phase of 45° for different frequencies (ranging from 0.3THz to 1THz) are illustrated in Figure 7. The main pattern direction of the antenna is towards “y” axe with the maximum directivity of 3.89 dBi. At 0.5THz the radiation pattern is dipolar, and above it, it starts to have side lobes as the frequency increases.
Conclusions
In this paper, a Multi-physics simulation for coupling all the phenomena involved in the generation of THz radiation with PC antennas is implemented using COMSOL Multiphysics 4.3b. Through this simulation, interesting characteristics of the antenna design and excitation parameters were obtained. Results indicate the role of each parameter in the resulting photocurrent waveform and THz frequency: the radiated THz photocurrent waveform is determined by the photoconductive gap (the separation between the metallic electrodes), the incident laser illumination and the DC excitation voltage; while the THz frequency depends on the length of the dipole. Thus this simulation should serve as a useful tool in designing PC antennas and tuning the excitation parameters for improving the operation of these devices.
Acknowledgements
The authors would like appreciating the Chemical Engineering Department, Universidad de los Andes for allowing the usage of COMSOL Multiphysics 4 .3b.
References
Armstrong, C. (2012). The truth about terahertz. IEEE Spectrum, 49(9), 36-41. doi:10.1109/MSPEC.2012.6281131 [ Links ]
Berry, C. W., Hashemi, M. R., & Jarrahi, M. (2014). Generation of high power pulsed terahertz radiation using a plasmonic photoconductive emitter array with logarithmic spiral antennas. Applied Physics Letters, 104(8), 081122. doi:10.1063/1.4866807 [ Links ]
Castro-Camus, E., Lloyd-Hughes, J., & Johnston, M. (2005). Three-dimensional carrier-dynamics simulation of terahertz emission from photoconductive switches. Physical Review B, 71(19), 195-301. doi:10.1103/PhysRevB.71.195301 [ Links ]
Chazan, P., Haelterman, M., & Tedjini, S. (1992). Influence of optical dispersion on the performances of an electrooptic phase modulator. IEEE Microwave and Guided Wave Letters, 2(1), 19-21. doi:10.1109/75.109130 [ Links ]
Chen, H.-T., Kersting, R., & Cho, G. C. (2003). Terahertz imaging with nanometer resolution. Applied Physics Letters, 83(15), 3009. doi:10.1063/1.1616668 [ Links ]
Criollo, C., Avila, A., & Winnerl, S. (2014). Estudio de Dispositivos Terahertz para Futuras aplicaciones en Biomédica. Universidad de los Andes. [ Links ]
Duvillaret, L., Garet, F., Roux, J.-F., & Coutaz, J.-L. (2001). Analytical modeling and optimization of terahertz time-domain spectroscopy experiments, using photoswitches as antennas. IEEE Journal of Selected Topics in Quantum Electronics, 7(4), 615-623. doi:10.1109/2944.974233 [ Links ]
Federici, J. F., Schulkin, B., Huang, F., Gary, D., Barat, R., Oliveira, F., & Zimdars, D. (2005). THz imaging and sensing for security applications-explosives, weapons and drugs. Semiconductor Science and Technology, 20(7), S266-S280. doi:10.1088/0268-1242/20/7/018 [ Links ]
Feng*, S., & Winful, H. G. (2001). Physical origin of the Gouy phase shift. Optics Letters, 26(8), 485. doi:10.1364/OL.26.000485 [ Links ]
Gupta, S., Whitaker, J. F., & Mourou, G. A. (1992). Ultrafast carrier dynamics in III-V semiconductors grown by molecular-beam epitaxy at very low substrate temperatures. IEEE Journal of Quantum Electronics, 28(10), 2464-2472. doi:10.1109/3.159553 [ Links ]
Hoffmann, J., Leuchtmann, P., Ruefenacht, J., & Hafner, C. (2009). Propagation Constant of a Coaxial Transmission Line With Rough Surfaces. IEEE Transactions on Microwave Theory and Techniques, 57(12), 2914-2922. doi:10.1109/TMTT.2009.2034214 [ Links ]
Khiabani, N., Huang, Y., Shen, Y., & Boyes, S. (2011). Time variant source resistance in the THz photoconductive antenna. In 2011 Loughborough Antennas & Propagation Conference (pp. 1-3). IEEE. doi:10.1109/LAPC.2011.6114091 [ Links ]
Kumar, S., Chan, C. W. I., Hu, Q., & Reno, J. L. (2011). A 1.8-THz quantum cascade laser operating significantly above the temperature of [planck][omega]/kB. Nat Phys, 7(2), 166-171. Retrieved from http://dx.doi.org/10.1038/nphys1846 [ Links ]
Lee, Y.-S. (2009). Introduction. In Principles of Terahertz Science and Technology SE - 1 (pp. 1-9). Springer US. doi:10.1007/978-0-387-09540-0_1 [ Links ]
Liu, T.-A., Tani, M., & Pan, C.-L. (2003). THz radiation emission properties of multienergy arsenic-ion-implanted GaAs and semi-insulating GaAs based photoconductive antennas. Journal of Applied Physics, 93(5), 2996. doi:10.1063/1.1541105 [ Links ]
Lloyd-Hughes, J., Castro-Camus, E., & Johnston, M. B. (2005). Simulation and optimisation of terahertz emission from InGaAs and InP photoconductive switches. Solid State Communications, 136(11-12), 595-600. doi:10.1016/j.ssc.2005.09.037 [ Links ]
Loata, G. C., Thomson, M. D., Löffler, T., & Roskos, H. G. (2007). Radiation field screening in photoconductive antennae studied via pulsed terahertz emission spectroscopy. Applied Physics Letters, 91(23), 232-506. doi:10.1063/1.2823590 [ Links ]
Löffler, T., Kreß, M., Thomson, M., Hahn, T., Hasegawa, N., & Roskos, H. G. (2005, July 1). Comparative performance of terahertz emitters in amplifier-laser-based systems - Abstract - Semiconductor Science and Technology - IOPscience. IOP Publishing. Retrieved from http://iopscience.iop.org/0268-1242/20/7/003/pdf/sst5_7_ 003.pdf [ Links ]
Ludwig, C., & Kuhl, J. (1996). Studies of the temporal and spectral shape of terahertz pulses generated from photoconducting switches. Applied Physics Letters, 69(9), 1194. doi:10.1063/1.117408 [ Links ]
Mickan, S. P., Shvartsman, R., Munch, J., Zhang, X.-C., & Abbott, D. (2004). Low noise laser-based T-ray spectroscopy of liquids using double-modulated differential time-domain spectroscopy. Journal of Optics B: Quantum and Semiclassical Optics, 6(8), S786-S795. doi:10.1088/1464-4266/6/8/025 [ Links ]
Saleh, B. E. A., & Teich, M. C. (1991). Beam Optics. In Fundamentals of Photonics (pp. 80-107). John Wiley & Sons, Inc. doi:10.1002/0471213748.ch3 [ Links ]
Shi, W., Hou, L., & Wang, X. (2011). High effective terahertz radiation from semi-insulating-GaAs photoconductive antennas with ohmic contact electrodes. Journal of Applied Physics, 110(2), 023111. doi:10.1063/1.3611397 [ Links ]
Spence, D. E., & Sibbett, W. (1991). Femtosecond pulse generation by a dispersion-compensated, coupled-cavity, mode-locked Ti:sapphire laser. Journal of the Optical Society of America B, 8(10), 2053. doi:10.1364/JOSAB.8.002053 [ Links ]
Tang, J., Deng, L. Y., Tay, C. B., Zhang, X. H., Chai, J. W., Qin, H., ... Chua, S. J. (2014). Determination of carrier concentration dependent electron effective mass and scattering time of n-ZnO thin film by terahertz time domain spectroscopy. Journal of Applied Physics, 115(3), 033111. doi:10.1063/1.4861421 [ Links ]
Tani, M., Kinoshita, T., Nagase, T., Ozawa, S., Tsuzuki, S., Takeshima, D., ... Bakunov, M. (2013). Techniques of non-collinear electro-optic sampling for efficient detection of pulsed terahertz radiation. In 2013 International Kharkov Symposium on Physics and Engineering of Microwaves, Millimeter and Submillimeter Waves (pp. 356-358). IEEE. doi:10.1109/MSMW.2013.6622077 [ Links ]
Tani, M., Matsuura, S., Sakai, K., & Nakashima, S. (1997). Emission characteristics of photoconductive antennas based on low-temperature-grown GaAs and semi-insulating GaAs. Applied Optics, 36(30), 7853. doi:10.1364/AO.36.007853 [ Links ]
Tani, M., Sakai, K., Abe, H., Nakashima, S., Harima, H., Hangyo, M., ... Tsukada, N. (1994). Spectroscopic Characterization of Low-Temperature Grown GaAs Epitaxial Films. Japanese Journal of Applied Physics, 33(9R), 4807-4811. doi:10.1143/JJAP.33.4807 [ Links ]
Tonouchi, M. (2007). Cutting-edge terahertz technology. Nature Photonics, 1(2), 97-105. doi:10.1038/nphoton.2007.3 [ Links ]
Venkatesh, M., Rao, K. S., Abhilash, T. S., Tewari, S. P., & Chaudhary, A. K. (2014). Optical characterization of GaAs photoconductive antennas for efficient generation and detection of Terahertz radiation. Optical Materials, 36(3), 596-601. doi:10.1016/j.optmat.2013.10.021 [ Links ]
Zhengqing Yun, M. F. I. (2000). Implementation of Floquet Boundary Conditions in FDTD Analysis of Periodic Phased Array Antennas with Skewed Grid. Electromagnetics, 20(5), 445-452. doi:10.1080/027263400750064437 [ Links ]













