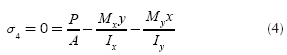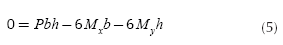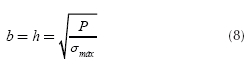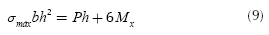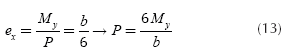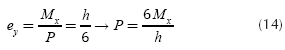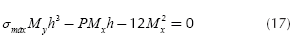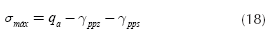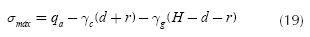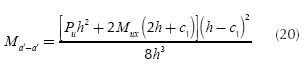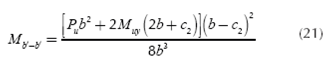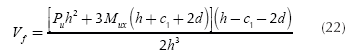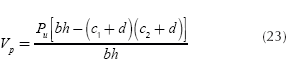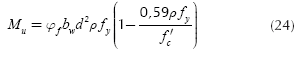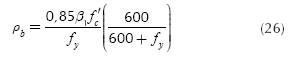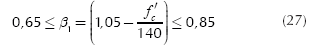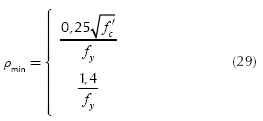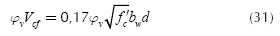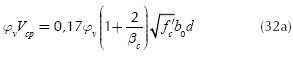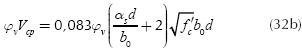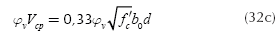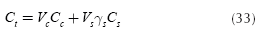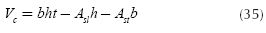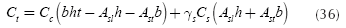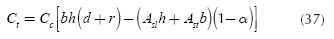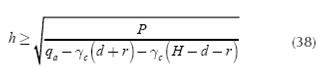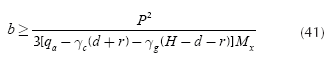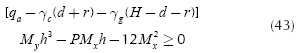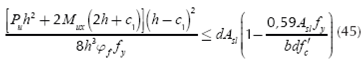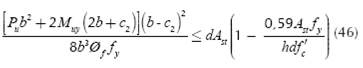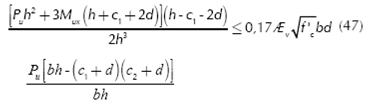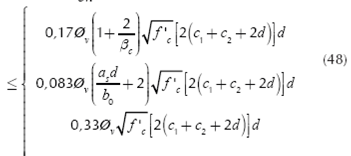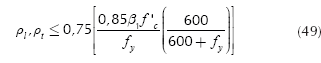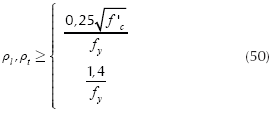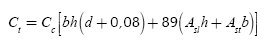Introduction
The foundation is the part of the structure which transmits the loads to the soil. The foundations are classified into superficial and deep, which have important differences: in terms of geometry, the behavior of the soil, its structural functionality and its constructive systems (Das et al., 2006; Ha, 1993).
The footings sizes are mostly governed by the axial load and moments, allowable soil pressure, unit weight of concrete, soil unit weight, and the depth of the footing base below the final grade (Al-Ansari, 2013).
Optimum design of structures has been the topic of many studies in the field of structural design. A designer's goal is to develop an "optimal solution" for the structural design under consideration. Normally, an optimal solution implies the most economic structure without impairing the functional purposes the structure is supposed to serve (Bhalchandra & Adsul, 2012).
The optimum design is generally considered to be the one design that best satisfies the criteria for the project. Typically, there is some kind of objective function that can be computed from the variables that define a design. The value of the objective function is used to compare feasible designs in order to determine the "best" or "optimum" design (Quimby, 2012).
The papers for optimal design of reinforced concrete foundations are: Flexural Strength of Square Spread Footing (Jiang, 1983); Closure to "Flexural Strength of Square Spread Footing" by Da Hua Jiang (Jiang, 1984); Flexural Limit Design of Column Footing (Hans, 1985); Economic Design Optimization of Foundation (Wang and Kulhawy, 2008); Reliability-Based Economic Design Optimization of Spread Foundation (Wang, 2009); Structural Cost of Optimized Reinforced Concrete Isolated Footing (Al-Ansari, 2013); Multi-objective Optimization of foundation using global-local gravitational search algorithm (Khajehzadeh et al., 2014).
Luévanos-Rojas (2013) presented a mathematical model for dimensioning of rectangular footings.
Luévanos-Rojas et al. (2013) proposed the design for isolated footings of rectangular form using a new model.
Luévanos-Rojas (2016b) presented a comparative study for the design of rectangular and circular isolated footings using new models.
This paper shows an optimal design for reinforced concrete rectangular footings using a new model. A numerical example is presented to show the model capability to estimate the minimum cost design of the materials used for a rectangular footing that supports an axial load and moments in two directions in accordance to the building code requirements for structural concrete (ACI 318-13) and commentary. Also a comparison is made between the optimal design and current design for rectangular footings in order to observe differences.
Methodology
Model for dimensioning of rectangular footings
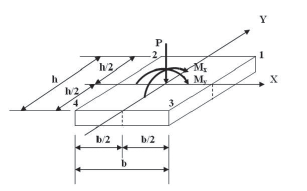
Figure 1 presents a rectangular footing subjected to axial load and moment in two directions (biaxial bending), where pressure is different in the four corners of the contact surface.
General equation for any type of footings subjected to biaxial bending is:
where: σ is the stress exerted by the soil on the footing (soil pressure), A is the contact area of the footing, P is the axial load applied at the center of gravity of the footing, Mx is the moment around the axis "X", My is the moment around the axis "Y", x is the distance in the direction "X" measured from the axis "Y" to the fiber under study, y is the distance in direction "Y" measured from the axis "X" to the farthest under study, ly is the moment of inertia around the axis "Y" and Ix is the moment of inertia around the axis "X".
The maximum stress is the available load capacity of the soil:
Substituting the values of A = bh, Cy = h/2, Cx = b/2, Ix = bh3/12 and Iy = hb3/12 into Equation (2) is obtained:
The minimum stress is zero:
Substituting the values of A = bh, Cy = h/2, Cx = b/2, Ix = bh3/12 and Iy = hb3/12 into Equation (2) is obtained:
First case. The axial load applied at the center of gravity of the footing (ex = 0 and ey = 0).
Substituting My = 0 and Mx = 0 into Equations (3) and (5) is obtained:
Substituting b = h into Equation (6) is found:
Note: the values of b and h are governed by the maximum stress, and these values of b and h must be the minimum values.
Second case. The axial load located to eccentricities ex= 0 and ey ≠ 0 (uniaxial bending).
Substituting My = 0 into Equations (3) and (5) is obtained:
The value of h by Equation (10) is found:
Substituting Equation (11) into Equation (9) is obtained:
Note: these values of b and h must be the minimum values.
Third case. The axial load is located to eccentricities ex ≠0 and ey ≠ 0 (biaxial bending).
The permitted maximum eccentricity for that the tensile stresses are not present in the soil is 1/6 the side of the footing. Then the eccentricities are defined as follows (Luévanos-Rojas, 2013):
The value of "P" in Equation (13) is substituted into Equation (14), and the value "b" is obtained (Luévanos-Rojas, 2013):
Now, substituting Equation (15) into Equation (5) is obtained (Luévanos-Rojas, 2013):
Substituting the Equation (15) into Equation (3) is obtained (Luévanos-Rojas, 2013):
when soil pressure is zero by Equation (16) the value of "h" is obtained, and when soil pressure is the available load capacity "σmax" by Equation (17) the value of "h" is found, and of the two values i s taken the greater of the two conditions, because the pressure generated by the soil on the footing must greater than zero and less than the available load capacity of the soil (Luévanos-Rojas, 2013).
The available load capacity of the soil " σmax " is (Luévanos-Rojas et al., 2013):
where: qa is the allowable load capacity of the soil, γppz is the self-weight of the footing in square meter, γpps is the self-weight of soil fill in square meter.
Note: if in the combinations are included the wind and/or the earthquake, the allowable load capacity of the soil can be increased by 33% (ACI 318-13).
Also, Equation (19) could be presented:
where: γc is concrete density = 24 kN/m3, γg is soil density, d is the footing effective depth, r is the footing coating and H is the depth of the footing base below the final grade.
Once the value of "h" is obtained, the value of "b" is found by Equation (15).
New model for design of rectangular isolated footings
According to Building Code Requirements for Structural Concrete and Commentary (2013), the critical sections are: 1) the maximum moment is located in face of column, pedestal, or wall, for footings supporting a concrete column, pedestal, or wall; 2) bending shear is presented at a distance "d" (distance from extreme compression fiber to centroid of longitudinal tension reinforcement) shall be measured from face of column, pedestal, or wall for footings supporting a column, pedestal, or wall; 3) punching shear is localized so that it perimeter "bo" is a minimum but need not approach closer than "d/2" to: (a) Edges or corners of columns, concentrated loads, or reaction areas; and (b) Changes in slab thickness such as edges of capitals, drop panels, or shear caps (ACI 318-13).
Critical sections for moments are presented in section a'- a' and b'-b', as shown in Figure 2.
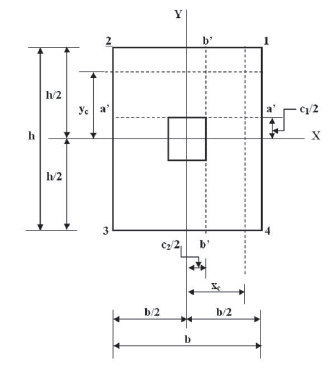
Source: (Luévanos-Rojas et al., 2013; Luévanos-Rojas, 2016b)
Figure 2 Critical sections for moments.
Moment "Ma-a" acting around the axis a'-a' is (Luévanos-Rojas et al., 2013; Luévanos-Rojas, 2016b):
Moment "Mb'-b'" acting around the axis b'-b' is (Luévanos-Rojas et al., 2013; Luévanos-Rojas, 2016b):
where: Pu is load; Mux and Muy are moments factored acting on the footing.
The critical section for bending shear (unidirectional shear force) is obtained at a distance "d" to from face of the column with the footing is presented in section c'- c' as seen in Figure 3.
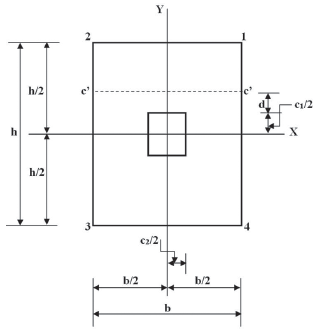
Source: (Luévanos-Rojas et al., 2013; Luévanos-Rojas, 2016b)
Figure 3 Critical section for bending shear.
Now, the bending shear "Vf" is (Luévanos-Rojas et al., 2013; Luévanos-Rojas, 2016b):
The critical section for the punching shear (bidirectional shear force) appears at a distance "d/2" to from of column face with the footing in the two directions in section formed by points 5, 6, 7 and 8; see Figure 4.
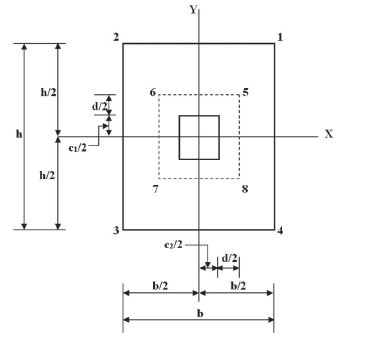
Source: (Luévanos-Rojas et al., 2013; Luévanos-Rojas, 2016b)
Figure 4 Critical section for punching shear.
Now, the punching shear "Vp" is (Luévanos-Rojas et al., 2013; Luévanos-Rojas, 2016b):
Equations provided by building code requirements for structural concrete and commentary (ACI 318-13)
Equations for moment in both axes are considered at the face of the column are (ACI 318-13; Luévanos-Rojas, 2016a):
where: Mu is the factored maximum moment, Øf is the strength reduction factor by bending, and its value is 0,90, bw is width of analysis in structural member, ρ is ratio of As to bd, β1 is the factor relating depth of equivalent rectangular compressive stress block to neutral axis depth, fy is the specified yield strength of reinforcement of steel, f'c is the specified compressive strength of concrete at 28 days.
Required strength U to resist factored loads or related internal moments and forces is (ACI 318-13):
where: D are the dead loads, or related internal moments and forces, L are the live loads, or related internal moments and forces.
Equation for the bending shear (unidirectional shear force) is considered at a distance "d" to from of column face is (ACI 318-13):
where: Vcf is bending shear resisting by concrete; Øv is the strength reduction factor by shear is 0,85.
Equations for the punching shear (shear force bidirectional) appears at a distance "d/2" to from of column face on the footing in the two directions are shown (ACI 318-13):
where: Vcp is punching shear resisting, βc is the ratio of long side to short side of the column, b0 is the perimeter of the critical section, αs is 40 for interior columns, 30 for edge columns, and 20 for corner columns. ØvVcp must be the largest value of Equations (32a), (32b) and (32c).
Objective function to minimize the cost
A cost function is defined as the total cost "Ct" which is equal to cost of flexural reinforcement more the cost of concrete. These costs involve material costs and fabrication costs, respectively. The cost of the rectangular footing is:
where: Cc is cost of concrete for 1 m3 of ready mix reinforced concrete in dollars, Cs is cost of reinforcement steel for 1 kN of steel in dollars, Vs is volume of reinforcement steel, Vc is volume of concrete and γs is steel density = 76,94 kN/m3.
The volumes for rectangular footings are:
Substituting Equations (34) and (35) into Equation (33) is obtained:
Substituting α = γsCs/Cc into Equation (36) is presented:
Constraint functions
Equations of the model for dimensioning of rectangular footings, the new model for design of rectangular isolated footings and the building code requirements for structural concrete (ACI 318-13) and commentary are considered to obtain the constraint functions.
For the dimensioning
First case:
Second case:
Third case:
For the design
where: ρl is ratio of reinforcement steel in direction the long side, ρt is ratio of reinforcement steel in direction the short side, Asl is reinforcement steel in direction the long side, Ast is reinforcement steel in direction the short side of the footing.
Application of the model
The design for a reinforced concrete isolated footing of rectangular form that supports a square column with the basic information following: c1 = 40 cm; c2 = 40 cm; H = 1,5 m; PD = 700 kN; PL = 500 kN; MDx =140 kN-m; MLx = 100 kN-m; MDy = 120 kN-m; MLy = 80 kN- m; f'c = 21 MPa; fy = 420 MPa; qa =220 kN/m2; γc=24 kN/m3; γg = 15 kN/m3/; r = 8 cm; α = 90. It is required to determine values of the optimum ratios of reinforcement steel ρl and ρt, the optimum areas of reinforcement steel Asl and Ast, the optimum dimensions of the footing b and h, and the optimum effective depth d.
Where: PD is dead load, PL is live load, MDx is moment around of axis "X-X" of dead load, MLx is moment around of axis "X-X" of live load, MDy is moment around of axis "Y-Y" of dead load, MLy is moment around of axis "Y-Y" of live load.
Loads and moments acting on soil are: P = 1200 kN, Mx = 240 kN-m, My = 200 kN-m.
Loads and moments acting on the footing by Equation (30) are factored: Pu = 1640 kN, Mux = 328 kN-m, Muy = 272 kN-m.
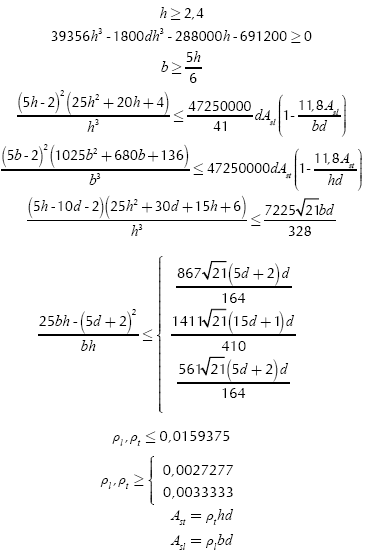
Substituting corresponding values into Equation (37) to obtain the objective function, and also into Equations (42) to (52) to find the constraints, these are:
Objective function to minimize the cost:
Subject to:
Assume all variables nonnegative.
The MAPLE-15 software for the optimization problem has been used to assess the optimal design with respect to minimum cost for the reinforced concrete rectangular footing using the new model.
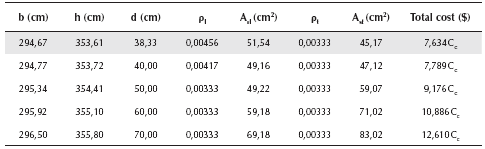
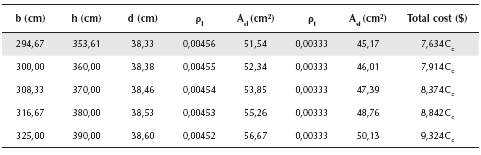
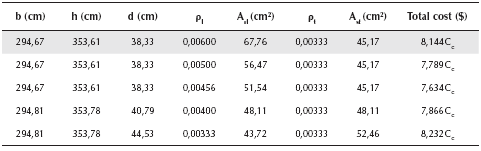
Now a numerical experimentation is developed by the optimal design model using Equation (37) and Equations (42) to (52). Also, results are verified by the standard design method using Equations (15) to (32a,b,c). The results are presented in Tables 1, 2, 3 and 4. Table 1 shows when the effective depth "d" takes into account the values of 38,33, 40,00, 50,00, 60,00 and 70,00 cm. Table 2 presents, when the short side "b" of the footing varies of 294,67, 300,00, 310,00, 320,00 and 330,00 cm. Table 3 presents when the long side "h" of the footing changes its value of 353,61, 360,00, 370,00, 380,00 and 390,00 cm. Table 4 shows when the ratios of reinforcement steel "ρl" varies its value of 0,00600, 0,00500, 0,00456, 0,00400 and 0,00333. In these tables are marked the derived optimum design formulae for the reinforced concrete isolated footings of rectangular form and, it gives an accurate estimate of the minimum material cost.
Results
Table 1 shows the numerical experimentation varying the effective depth "d". When the value of "d" is increased, the values of "ρ l " and "Asl" are reduced until the minimum value of " ρ l " and to from of this value "Asl" is increased; the values of "Ast,", "b" and "h" are increased; the value of "ρt" is constant, and the total material cost is greater.
Table 2 presents the numerical experimentation modifying the dimension the short side "b" of the footing. When the value of "b" is increased, the values of "Ast,", "h" and "d" are increased; the values of " ρ l " and "Asl" are reduced; the value of "ρ t " is constant, and the total material cost is larger.
Table 3 shows the numerical experimentation changing the dimension the greater side "h" of the footing. When the value of "h" is increased, the values of "Asl.", "Ast,", "b" and "d" are increased; the value of "ρ l " is reduced; the value of "ρ t " is constant, and the total material cost is greater.
Table 4 presents the numerical experimentation varying the ratios of reinforcement steel "ρ l ". When the value of "ρ l " is reduced, the value of "Asl" is reduced; the values of "b", "h", "d" and "Ast," are increased; the value of "ρt," is constant, and the total material cost is reduced until the cost of 7,634C , and to from of this value is increased.
The corresponding total material cost Ct of the rectangular isolated footing is obtained from Equation (37) that is 7,634C as minimum value in terms the concrete cost, and numerical experimentation presented by the optimal design model and standard design method are verified.
Conclusions
This study deals the design of minimum cost for reinforced concrete isolated footings of rectangular form subjected to a concentrated load and moments in two directions using the new model generalized.
A mathematical approach of the problem based on a criterion of minimum cost design and a set of constraints in accordance to the building code requirements for structural concrete (ACI 318-13) and commentary are formulated. We assume that the constant parameters are: c1, c2, H, P, Mx , My , qa , γ c , γ g , r, α, f'c and fy , the design variables are: b, h, d, ρ l , ρ t , Asl and Ast.
The optimal design equations obtained for the reinforced concrete rectangular isolated footings using the new model give a very accurate estimate of the minimum cost.
Using the optimal design, this paper successfully acquires a model to predict the ratios of reinforcement steel ρ l and ρ t , the optimum areas of reinforcement steel Asl and Ast, the optimum dimensions of the footing b and h, the optimum effective depth d and minimum cost for reinforced concrete rectangular isolated footings subjected to a concentrated load and moments in two directions generalized.
The optimal design model proposed in this paper can be used for other codes of design, modifying the equations of the factored moments, bending shear resisted by concrete and punching shear resisted by concrete to obtain the total material cost for the reinforced concrete rectangular isolated footings.