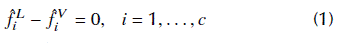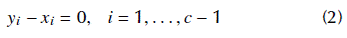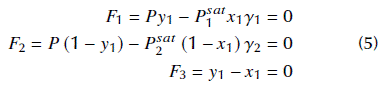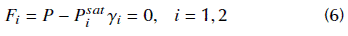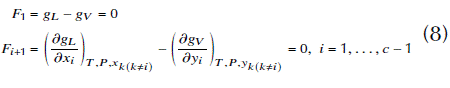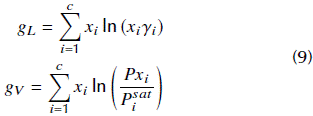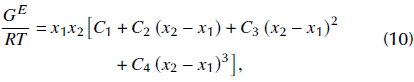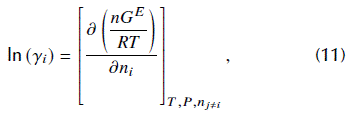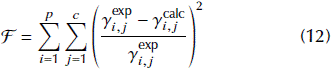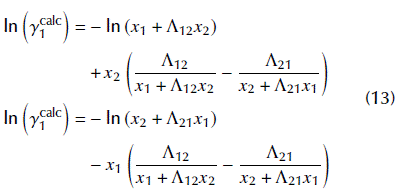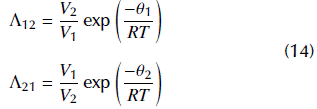Introduction

Multimodal optimization problems can be a challenging test for stochastic optimization algorithms (^{Platt, 2016}), considering the task of locating all minimum/maximum points of the problem at hand. This kind of problem has been studied with crowding, sharing, niching and speciation techniques, among others (^{Thomsen, 2004}; ^{Parrot and Li, 2006}; ^{Cuevas and Reyna-Orta, 2014}). In these scenarios, versions of established algorithms were developed for multimodal problems, such as the Crowding DE (Crowding Differential Evolution), the Sharing DE (Sharing Differential Evolution) (^{Thomsen, 2004}) and the SPSO (species-based Particle Swarm Optimization) (^{Parrot and Li, 2006}). A revision regarding these techniques was presented by ^{Parrot and Li (2006)}.

Recently, new approaches have been published to deal with multimodal problems. Standing out among them - in terms of simplicity of implementation - are the Multimodal Cuckoo Search (MCS) (^{Cuevas and Reyna-Orta, 2014}) and the Multimodal Flower Pollination Algorithm (MFPA) (^{Gálvez, Cuevas, and Avalos, 2017}). These algorithms were tested in typical benchmark functions, but lack tests and validation in real engineering problems.

Stochastic optimization algorithms have been extensively used in many fields of engineering in the last decades (^{Bermeo, Caicedo, Clementi, and Vega, 2015}; ^{García Montoya and Mendoza Toro, 2011}; ^{Nagarkar and Vikhe, 2016}). In this scenario, the present work presents some applications of the MFPA algorithm in two phase equilibrium problems: (i) an application in refrigeration; the calculation of azeotropic composition in the mixture HFC4310mee (commercially known as Vertrel XF) + Tetrahydrofuran (THF), a refrigerant fluid - refrigerant fluids are usually pure substances or azeotropic mixtures; zeotropic mixtures are avoided in refrigeration, since the composition variations arising from vaporization and condensation processes can alter the performance of the refrigerator - and (ii) the parameter estimation in the binary system acetic acid + anisole, a system with applications in the agrochemical industry. The vapor-liquid equilibrium in the system acetic acid + anisole was recentlystudied by ^{Mali, Mali, Patil, and Joshi (2017)}. The anisole exhibits insecticide properties and has been studied in recent years (^{Quan, Liu, and Liu, 2018}). ^{Platt (2016)} discussed the performance of two stochastic algorithms in the azeotrope calculations, yetemploying adifferentapproach to the used in this work, mainly regarding the strategies used to obtain multiple solutions.

The aim of this work is not to present comparisons between the different existing techniques to solve multimodal problems. Such comparisons have been exhaustively discussed in the literature (see ^{Derrac, García, Molina and Herrera, 2011}; ^{Platt, Yang and Silva Neto, 2019}) and the results are intrinsically dependent on the parameters used in the algorithms, which renders these analyses arbitrary under several aspects. Thus, the objective of this work is to verify the applicability, in terms of robustness or efficiency (with respect to the identification of the solutions of the problems) and ease of implementation, of the MFPA in real engineering problems. A recent analysis of algorithm comparisons (bio-inspired metaheuristics and deterministic approaches) was presented by ^{Sergeyev, Kvasov, and Mukhametzhanov (2018)}. These authors conclude that both metaheuristics and determinist algorithms were capable to adequately solve distinct problems, and that, obviously, the parameter tuning of metaheuristics must be considered in such comparisons.

Description of the problems

Azeotrope Calculation

The term azeotrope refers to a thermodynamic condition where a boiling liquid produces a vapor phase with the same composition. The existence of azeotropes can occasionally cause problems in the separation of the mixture by distillation (see ^{Shen, Benyounes, and Song, 2015}).

The azeotrope calculation will be modeled with two distinct approaches, in order to evaluate the effect of the objective function (or fitness, to use a bio-inspired term). Obviously, the solution for both formulations are the same.

Formulation 1: The first approach consists in the azeotropy problem in its classical formulation, i.e., the isofugacity equations and the equality of compositions between liquid and vapor phases (azeotropy relation) (^{Walas, 1985}):

where 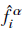is the fugacity of component i (in the mixture) in phase a, in a mixture with c components. The superscripts L and V refer to the liquid and vapor phases, respectively. The molar fractions of the component i in liquid and vapor phases are X _i and y _i , respectively. Equations (1) impose the coexistence of the phases, and Equations (2) represent the equality of compositions between liquid and vapor phases (representing pure components and azeotropes). As a condition of coexistence, the azeotropy also implies the equalities of temperatures and pressures for both phases. Since we are using only one temperature (T) and one pressure (P) for vapor and liquid phases, these conditions are implicitly attended. The fugacity of a component i in the vapor phase will be calculated considering an ideal vapor phase - which is compatible with the low pressures in the studied problems - which produces (^{Walas, 1985}):

The nonideal liquid phase will be modeled by a modified Raoult's law (^{Walas, 1985}):

where P ^sat _i is the saturation pressure of the pure fluid i and ү _i is the activity coefficient of component i. In a binary system, we obtain:

Substituting F ₃ in F ₁ and F ₂ , a two-dimensional problem (to be zeroed) can be obtained:

The fitness function ℱ can be produced by adding the squares of the residues of each nonlinear equation, i.e.:

Null minima of ℱ are the solutions (or roots, using the widespread term employed in numerical analysis) of the nonlinear system represented by Eqs. (6).

Formulation 2: Considering the approach of ^{Bonilla-Petriciolet, Iglesias-Silva, and Hall (2009)} (referred here as Formulation 2), the azeotrope calculation can be represented as:

where g refers to the dimensionless molar Gibbs free energy of mixing for the mixture 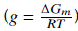, represented by

for liquid and vapor phases, respectively. Again, if we consider y_i = x_i, ∀i, the azeotropy problem is solved for liquid molar fractions. The fitness function is, again, the sum of the residues of each nonlinear equation, and it can be calculated by using the same expression of Eq. (7), but now referring to the residues represented by Eq. (8).

In both cases, the molar excess Gibbs free energies (G ^E ) will be modeled by a Redlich-Kister model (^{Segura, González, and Wisniak, 2005}):

where 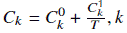= 1, 4. In the last equation, R is the Universal gas constant and T is the absolute temperature (Kelvin). Values for the coefficients and C⁰ _k and C¹ _k coefficients for Antoine's equation (for calculation of saturation pressures) are reported by ^{Segura et al. (2005)}.

The activity coefficients are partial molar properties of excess Gibbs free energies, and can be calculated by (^{Walas, 1985}):

where w is the total amount of substance.

Parameter Estimation

Parameter estimation is a very common task in many engineering fields. In the context of chemical engineering, the parameter estimation in thermodynamic models can exhibit multiple solutions, as pointed by ^{Gau, Brennecke, and Stadtherr (2000)}. In these occasions, the use of deterministic algorithms, such as the ^{Nelder-Mead Simplex (Nelder and Mead, 1965}), is not advisable, since local optima can be found depending on the initial guesses, which justifies the use of stochastic approaches. Thus, parameter estimation is a good scenario to test the performance of MFPA.

^{Mali et al. (2017)} studied the vapor-liquid equilibrium in the binary system acetic acid + anisole at 96,15 kPa. The experimental data described by them indicated a minimum boiling azeotrope in the system, close to the pure acetic acid in the compositional domain. The fitness function employed here is (^{Gau et al., 2000}):

where p is the number of experimental points and c is the number of components in the mixture. The superscripts exp and calc represent, respectively, experimental and calculated data. It must be stressed that this objective function is different to that employed by ^{Mali et al. (2017)}. These authors used an absolute deviation between calculated and experimental saturation pressures. The experimental data will be adjusted to the ^{Wilson model (1964)}. In this problem, since we are dealing specifically with the excess Gibbs free energy model, a more detailed description of the expressions is useful. The activity coefficients calculated by this model in a binary mixture are:

and the parameters Λ₁₂ and Λ ₂₁ are calculated by:

V₁ and V₂ are the molar volumes of components 1 and 2, respectively. The parameters (to be estimated in the optimization procedure) are θ1 and θ2. The experimental points are calculated by the modified Raoult's Law (^{Walas, 1985}). The experimental data employed in the parameter estimation (as well as all the other quantities, such as molar volumes and expressions for saturation pressures) are presented in ^{Mali et al. (2017)} and, for the sake of conciseness, are not reproduced here.

Methodology

In this section, we will present a brief description of the Multimodal Flower Pollination Algorithm (MFPA), proposed by ^{Gálvez et al. (2017)}. The original Flower Pollination Algorithm (FPA) was proposed by ^{Yang (2012)} and mimics the process of flower pollination. In FPA, a population (a set) of w flowers (vector of decision variables) is generated every k iteration (a generation), where each flower corresponds to a vector as a potential solution of the optimization problem. The quality of each vector is evaluated through a fitness function. At each iteration, either one of two operators is carried out for each individual population member: (i) local pollination operator, a small step, related to the exploitation of the promising regions and the accuracy of the solutions; or (ii) global pollination operator, a large step, using the Lévy Flight, responsible for exploring the domain in an effective way (^{Pavlyukevich, 2007}). A switch probability function is used in order to randomly define which operator is to be used. Finally, a elitism strategy is applied in order to keep the best solution (with the minimum cost function value in a minimization problem). The procedure is repeated until the maximum number of iterations (or generations) is achieved. At the end, the best solution found is a potential global optimum.

^{Gálvez et al. (2017)} proposed a multimodal flower pollination algorithm (MFPA) enhancing the original algorithm with multimodal capabilities, in which they added the process of finding the global optimum and multiple local optima. In the MFPA, three new elements are included. The first element involves a memory mechanism, which allows an efficient registering of potential optima. The memory is a set of vectors considered as the potential global or local optima. The second element is a new selection strategy approach, in order to decide whether the solution is to be registered as potential or not, thus updating the memory. The decision to keep the solution is influenced not only by the current best solution as in the original algorithm, but also by vector solutions that are contained in the memory. The third element consists of a depuration procedure executed in order to eliminate similar solutions that may represent the same optima, resulting in a cleaner memory (with less elements). Thus, the algorithm is summarized as follows: after the generation of the new population (by local or global pollination-FPA algorithm) and the initialization of the memory with the best solution from the first population, the new selection approach is executed and the memory is updated. Afterwards, the depuration procedure is executed and the memory is updated again. At the end, all memory solutions are supposed to be optimal (globally and locally).

The selection approach uses some rules based on the cost function of the solution to capture memory elements. The fitness value of the current vector is compared to the worst memory element. The distance to the nearest element in the memory is used to decide whether the solution represents a new optimum or is similar to an existing memory element. After the memory mechanism procedure, the depuration procedure is applied, in which the memory elements in the vicinity, within a ratio that depends on the distance between the elements, are cut off. Therefore, some elements that represent the same solution are excluded and, as a result, the memory contains a smaller number of solutions. Finally, the memory elements are expected to be the local and global optimum. In this work, the switch probability (between global and local pollination) was 0,25, the population size was fixed in 50 individuals and the number of iterations (stopping criterion) was 500. These are the same parameters proposed by ^{Gálvez et al. (2017)}. In fact, we are using the same set of parameters presented in the original algorithm, since a desirable property of any metaheuristic is the ability to deal with different problems without costly and difficult parametrization procedures.

Results and Discussions

Azeotrope calculation

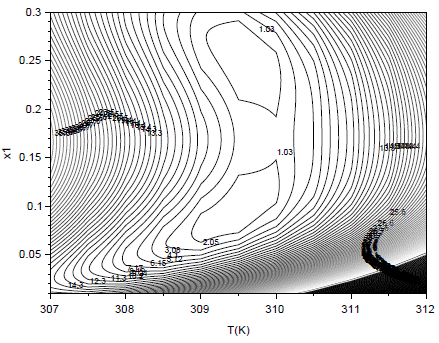
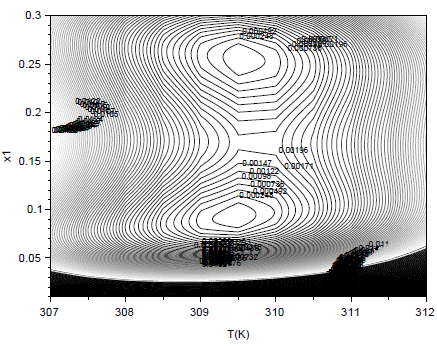
The azeotropic coordinates for the system HFC4130mee (1) + THF (2) at 35 kPaare (x₁,T) = (0,0924, 309,45) (Azeotrope 1) and (x₂,T) = (0,255,309,57) (with T in Kelvin), as reported by ^{Guedes, Moura Neto, and Platt (2015)}. As previously described as detailed by several authors (^{Segura et al., 2005}; Guedes et al., 2015), two azeotropes appear at this pressure. We observed that the values for the azeotropic temperatures are extremely close, which can be a challenge for the algorithm.

The contour curves of the fitness functions for Formulation 1 and Formulation 2 are presented in Figures 1 and 2, respectively. Clearly, one can note visible differences between the shapes of the contour curves related to the different formulations (even considering that the solutions are the same). We investigated the effect of these differences in the robustness of the methodology used to determine the azeotropic coordinates.

Source: Authors

Figure 1 Contour curves for the azeotropy problem (Formulation 1). 

Source: Authors

Figure 2 Contour curves for the azeotropy problem (Formulation 2). 

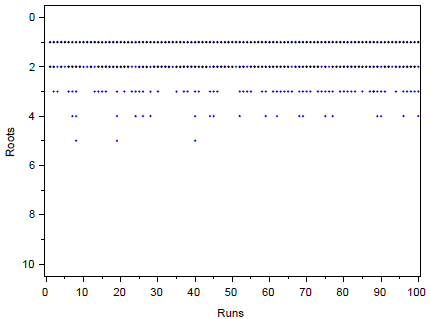
The algorithm was run 100 times for both formulations, in order to evaluate the performance of the computational framework, i.e., the capability to obtain, in a robust way, the exact number of solutions for each problem. A "run" is a typical execution of the MFPA, using random initial guesses. We noted that Formulation 1 found a larger number of roots when compared with Formulation 2. Since the problem exhibits only two solutions (roots), this behavior must be investigated. Figure 3 contains a graphical vision of a matrix containing the roots identified in each run, for both formulations. We observed that the algorithm identified (using Formulation 1, marked as blue points), in some occasions, more than two roots (up to five, in fact; an undesirable characteristic of the algorithm, related to the memory of the framework). On the other hand, using Formulation 2 (again in Figure 3, but now using black points) the algorithm found more than two solutions only in one run. But, in some runs, only one solution was identified, as indicated by the line corresponding to the second solution in Figure 3. This means that the algorithm "fails" to obtain all the solutions. The high fitness values for solutions (or roots) 3, 4 and 5 (typically non-physical solutions of the problem) indicate some kind of 'trash' in the memory of the algorithm (even using the memory depuration procedure), since we must obtain fitness values close to zero in the azeotropy problem.

Source: Authors

Figure 3 Matrix of roots found after 100 runs - azeotropy problem. 

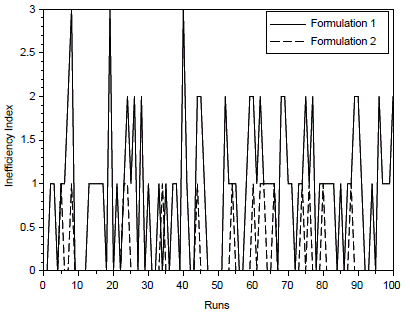
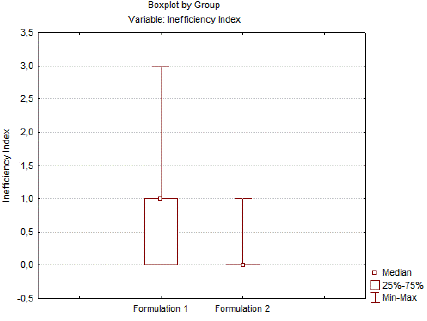
Considering this complex situation - one formulation finds more than two solutions, while the another one identifies less than two solutions - we used a tailor-made inefficiency index (ineff), defined as follows: ineff = (number of roots found) - (number of feasible roots found). For instance, if the algorithm found four roots and only one root corresponds to a physical one, the inefficiency is ineff = 4 - 1 = 3. On the other hand, if the program identifies 2 solutions and both are physical solutions, the index is ineff = 2 - 2 = 0. Figure 4 compares the inefficiency indexes for Formulations 1 and 2. An analysis of the figure appears to indicate that Formulation 2 is more efficient when compared to Formulation 1, but some statistical analysis is necessary.

Source: Authors

Figure 4 Inefficiency index for the azeotropy problem. 

Statistical Analysis

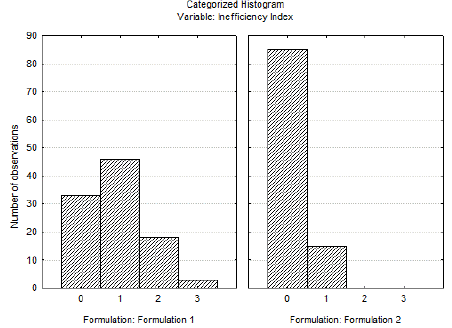
Formulations 1 and 2 were statistically compared with respect to the inefficiency at obtaining both solutions. A normality test was used to evaluate the distribution. A qualitative overview of the data can be performed by evaluating the categorized histogram (Figure 5). As observed, the data seems to be very far from normal distribution. This is supported by the Shapiro-Wilk parametric hypothesis test (^{Platt et al., 2019}), where the p-Values obtained for samples of Formulation 1 and Formulation 2 were both below the alpha risk of 5% (< 1 x 10^-5).

Source: Authors

Figure 5 Categorized histogram of the inefficiency index. 

As the normality hypothesis does not apply, and the objective is to compare independent results, a nonparametric test for unpaired data is applicable. The Mann-Whitney U test was used to verify if is there a shift or significant differences between the two samples (^{Platt et al., 2019}). The p-Value found for Formulation 1 versus Formulation 2 is 1, 36 x 10^-14. Thus, significant differences were found between the two populations.

In order to verify how different they are, the confidence interval was evaluated. As presented in the box plot in Figure 6, Formulation 2 presents a lower inefficiency index value and more confined variability, meaning that Formulation 2 presents a better performance than Formulation 1.

Source: Authors

Figure 6 Boxplot of the inefficiency index by formulation. 

Parameter Estimation

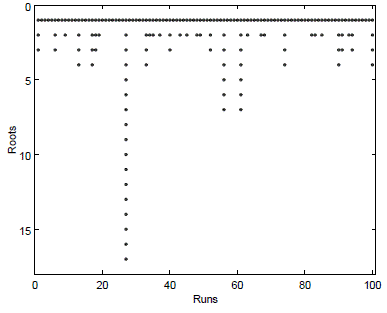
The search is conducted in the interval [-1000,1000] for both parameters (in fact, the search for binary interaction parameters for activity coefficient models is considered an unconstrained problem). The global minimum for this problem is θ ₁ = 426,24 and θ ₂ = 128,52 (obviously, this solution is different to that presented by ^{Mali et al., 2017}, since they used different objective functions). Only one minimum is found in this problem. In spite of this, we tested the multimodal algorithm, since in many real-world problems we do not previously know the number of minima/roots for each problem. Using the same procedure described above, the algorithm was executed 100 times, in order to evaluate the capability to obtain the expected solution in a robust manner.

Figure 7 contains the matrix of identified roots in 100 runs. Again, we confirm that the memory is contaminated in some runs with repeated solutions and/or not converged points. An outlier was found in the 27th run, with 17 roots stored in the memory (this kind of anomalous situation is common in stochastic algorithms). On the other hand, the solution of the problem was accurately identified in all runs, indicating that the computational framework was capable to obtain the minimum of the problem satisfactorily.

Source: Authors

Figure 7 Matrix of roots found in 100 runs - Parameter estimation problem. 

Finally, Figure 8 depicts the vapor-liquid equilibrium diagram at 96.15 kPa for the system acetic acid (1) + anisole (2). It is noted that the bubble and dew point curves produced with the estimated parameters show a good agreement with the experimental data published by ^{Mali et al. (2017)}. Furthermore, a minimum boiling azeotrope close to the pure acetic acid can be predicted.

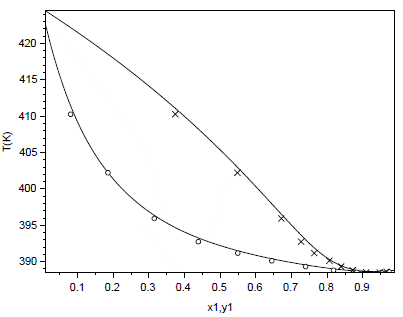
Source: Authors

Figure 8 Phase equilibrium diagram for the system acetic acid (1) + anisole (2) at 96,15 kPa. Experimental points published by ^{Mali et al. (2017)} are represented by "o" (liquid phase) and "x" (vapor phase) 

Conclusions

In this work, we tested a recently proposed strategy for multimodal problems - the Multimodal Flower Pollination Algorithm (MFPA) - in two chemical engineering problems: the calculation of a double azeotrope and the parameter estimation of a thermodynamic model.

Furthermore, we formulated the azeotropy calculation problem using two approaches. The MFPA algorithm was executed 100 times for each problem formulation. The results indicated a statistical difference between the two formulations employed in the double azeotropy problem, favoring the strategy proposed by ^{Bonilla-Petriciolet et al. (2009)}. In the parameter estimation problem, the algorithm identified repeated solutions, but was capable to find the minimum in all runs.

Finally, the computational results indicated that MFPA is a useful tool in real engineering optimization problems with multiple solutions.