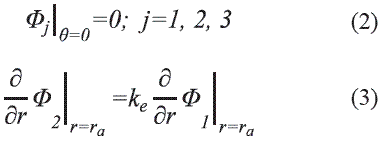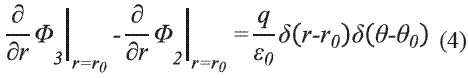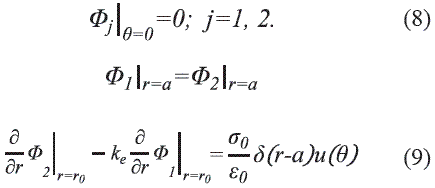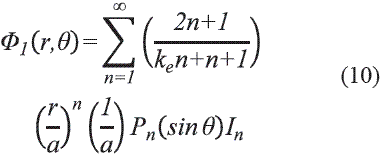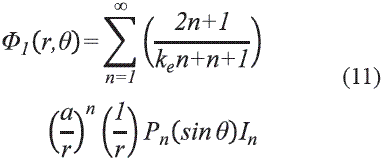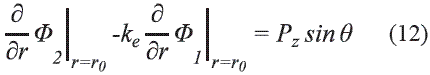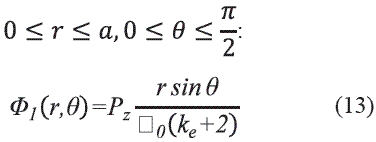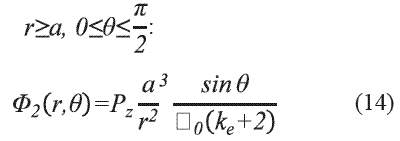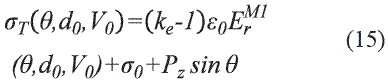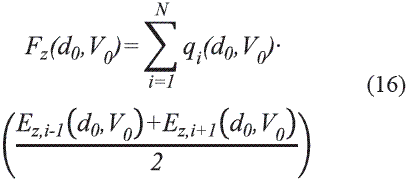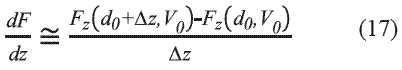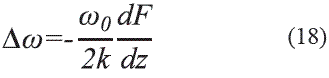Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230On-line version ISSN 2422-2844
Rev.fac.ing.univ. Antioquia no.50 Medellín Oct./Dec. 2009
Interacción punta-muestra dieléctrica en microscopía de fuerza electrostática
Electrostatic tip-dielectric sample interaction in electrostatic force microscopy
Ariel Gómez 1, Alba Graciela Ávila1, Gergory Ibrahim Massy2
1Centro de Microelectrónica de la Universidad de los Andes, Carrera 1 No 18A-10 Bogotá, Colombia.
2Grupo de Electrónica y Sistemas de Telecomunicaciones de la Universidad de los Andes, Carrera 1 No 18A-10 Bogotá, Colombia.
Resumen
La microscopía de fuerza electrostática es una técnica de medición de propiedades eléctricas locales de materiales. Las mediciones de gradiente de fuerza eléctrica sobre muestras dieléctricas son sensibles no sólo a la distribución de carga inicial en la misma sino también a la carga inducida por la punta de prueba conductora. Interpretar las contribuciones de cada efecto de forma independiente constituye un reto vigente de la técnica. Se introduce un modelo teórico que permite estudiar los efectos de carga e inducción para muestras y puntas de prueba con geometrías reales. El mismo modelo a partir de mediciones de gradiente de fuerza estima la carga inicial de la muestra. Las estimaciones de gradiente de fuerza reproducen mediciones experimentales realizadas en muestras dieléctricas cargadas.
Palabras clave: Electrostática, inducción de carga, gradiente de fuerza, AFM, EFM, electret, cantilever, viga voladiza, dieléctricos cargados
Abstract
Electric force microscopy is a local technique for measuring electrical properties of materials. The electrostatic force gradient measurements on dielectric samples are sensitive not only to the initial charge distribution in the sample but also to the charge induced by the conductive bias cantilever. Interpreting the contribution of each single effect on the charge distribution images is a challenge in the existing EFM technique. Here, a theoretical model is introduced to study the charge and induction effect on charged dielectric samples and commercial geometries for EFM tips. This model estimates the initial charge of the sample based on force gradient measurements. Gradient force results reproduce experimental measurements performed on electrets samples.
Keywords: Electrostatics, charge induction, force gradient, AFM, EFM, electret, cantilever
Introducción
La microscopía de barrido (SPM por sus siglas en inglés, Scanning Probe Microscopy) permite medir las propiedades electromecánicas de muestras micro y nanométricas con alta precisión. Una de las técnicas, ampliamente conocida, es microscopía de fuerza atómica (AFM por sus siglas en inglés, Atomic Force Microscopy). El AFM además de realizar las medidas de topografía y fuerza sobre muestras, mide potenciales y campos electrostáticos, relacionados con la carga, independientemente de la resistividad de la muestra; a esta extensión del AFM, se le conoce como microscopía de fuerza electrostática (EFM por sus siglas en inglés, Electrostatic Force Microscopy) [1,2].
La técnica EFM requiere de una viga voladiza (cantilever en inglés) en cuyo extremo se adhiere una punta de prueba metálica con el objetivo de medir las distribuciones de carga. Un control de posicionamiento barre la muestra que yace sobre una base a un potencial de referencia y va registrando la interacción eléctrica punto a punto. En uno de los modos de operación más usados la viga voladiza es excitada mecánicamente y oscila a su frecuencia de resonancia a un potencial V0 constante, método conocido como gradiente de campo eléctrico. En cada posición se registra el cambio de frecuencia de la viga voladiza con respecto a su frecuencia de resonancia, producida por la interacción electrostática puntamuestra. La distancia punta-muestra se mantiene a una distancia constante durante el barrido, lo suficientemente lejos para que predominen las fuerzas electrostáticas (Lift Mode). Una de las ventajas más significativas de este tipo de pruebas es que son no destructivas y poco invasivas [1-4]. Por su capacidad para estudiar muestras no conductoras, la técnica EFM se hace imprescindible para el estudio de las propiedades eléctricas de materiales dieléctricos a pequeña escala. Para modelar las interacciones entre la punta de prueba de la viga voladiza y una muestra dieléctrica se han desarrollado diferentes modelos teóricos en los últimos años. En ellos, se busca reproducir la geometría de la punta de prueba con gran precisión debido al largo alcance de las fuerzas electrostáticas. Sin embargo, la muestra casi siempre se toma como una lámina dieléctrica delgada sin carga inicial, despreciando cualquier tipo de curvatura de la misma y los efectos de carga [5-9].
En este artículo se presenta un modelo más complejo que toma en cuenta la interacción electrostática entre una muestra dieléctrica semiesférica con carga superficial inicial constante y una punta de prueba cónica. Así, se pueden estudiar dieléctricos cargados (electrects) no planos y predecir el comportamiento del gradiente de fuerza en función de la carga inicial. Además, se establece la influencia de la inducción de carga de la punta de prueba sobre este tipo de muestras, lo cual es una pregunta vigente en la comunidad científica. Posteriormente, se obtiene la solución numérica del cambio de frecuencia con respecto a la frecuencia de resonancia de la viga voladiza y se compara con resultados experimentales basados en modo de medición de gradiente de campo eléctrico [5, 10].
Modelo teórico
Uno de los mayores problemas que se presentan cuando se modela la interacción electrostática en un AFM es tener en cuenta geometrías reales de la punta de prueba y la muestra ya que generalmente los modelos asumen geometrías simplificadas. Por ejemplo, se usan modelos de placas infinitas paralelas para describir el sistema punta-muestra en cuyo caso se supone un campo eléctrico constante y se pierde el efecto de la geometría [11].
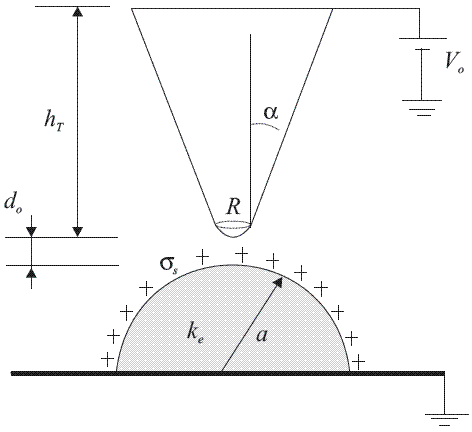
Figura 1 Vista 2D del modelo de sistema: punta de prueba conductora cónica con potencial V0 y muestra semiesférica dieléctrica de radio a y constante dieléctrica ke sobre un plano de tierra infinito. La distancia punta-muestra es d0 y el radio de punta R. El ángulo de la sección cónica esα
En la figura 1 se muestra el modelo desarrollado que toma en cuenta geometrías no planas de la muestra y comerciales de la punta [4, 12]. La punta de prueba se modela en su extremo como un cascarón esférico de radio R unido a una superficie cónica conα como ángulo mitad. La muestra se considera una semiesfera dieléctrica de radio a y permitividad relativa ke sobre un plano de tierra conductor infinito (en los montajes experimentales, la muestra es generalmente mucho menor que el porta muestras). Además, se añade al modelo una densidad de carga inicial en la superficie del dieléctrico con lo cual se reproduce una muestra dieléctrica cargada. Se considera que la punta de prueba esta a una distancia d0 de la muestra y que se aplica un potencial V0 a la misma.
El modelo tiene en cuenta el principio de superposición en la teoría electrostática para dividir el problema original en varios sub-problemas más simples y sumar las contribuciones de cada uno de ellos [13]. Tomando en cuenta lo anterior, se discretiza la punta en un conjunto de anillos. Posteriormente se resuelve el problema electrostático para cada uno de ellos y se superponen las soluciones de los mismos. Con esto se tiene el potencial y el campo eléctrico en el espacio debido a la punta discreta. Luego se hace una manipulación matemática con el objetivo de obtener un potencial constante en la superficie de la punta de prueba y, de esta manera, se garantiza que el campo eléctrico tangencial a la superficie sea aproximadamente cero cumpliéndose la condición de un material conductor [13]. Para este propósito se tendrá en cuenta la influencia de la carga inicial superficial sobre el dieléctrico. Por último se hacen cálculos de fuerza y gradiente de fuerza en la punta de prueba que sirven para validar el modelo.
Discretización de modelo de la punta
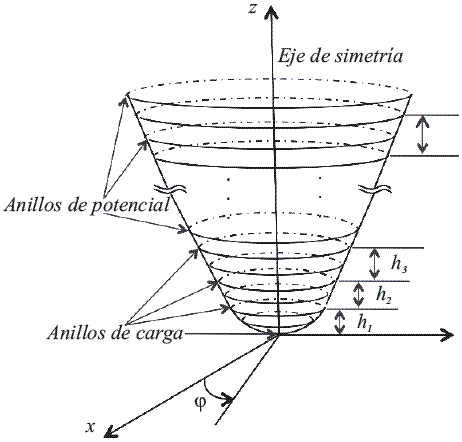
Para la solución analítica del potencial del modelo se discretiza la superficie de la punta definiendo un conjunto de NA anillos de carga qi, i 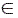 [1,NA] que poseen el mismo eje central (Figura 2). Con esto se garantiza simetría con respecto a la variable Φ en coordenadas esféricas.
[1,NA] que poseen el mismo eje central (Figura 2). Con esto se garantiza simetría con respecto a la variable Φ en coordenadas esféricas.
Los anillos están separados, en dirección Z, a distancias hi, i  [1, NA-1]. Para evaluar el potencial en la superficie de la punta se escogen NA anillos de potencial que se ubican en la mitad entre dos anillos de carga consecutivos.
[1, NA-1]. Para evaluar el potencial en la superficie de la punta se escogen NA anillos de potencial que se ubican en la mitad entre dos anillos de carga consecutivos.
Potencial de sistema anillo de carga sobre semiesfera dieléctrica en un plano de tierra
El problema a solucionar es el cálculo de potencial debido a un anillo de carga qi sobre una semiesfera dieléctrica que yace en un plano de tierra conductor infinito. Para este propósito se soluciona la ecuación de Laplace para el potencial Φ(r, θ) en coordenadas esféricas:
Figura 2 Discretización de la punta de prueba en anillos de carga y anillos de potencial. Los valores corresponden a la distancia entre anillos de carga y φ es el ángulo azimutal
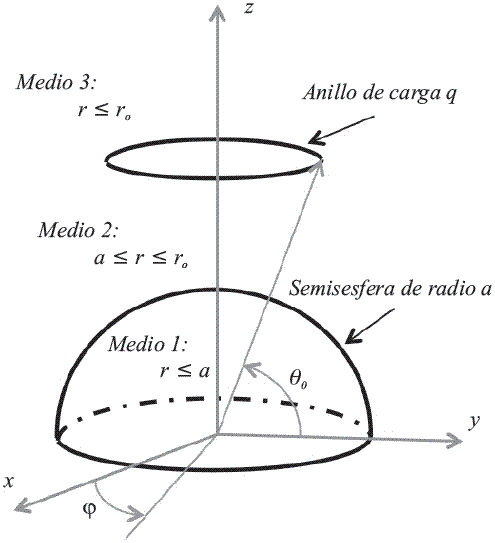
Se tiene en cuenta que existen tres medios diferentes (Figura 3), bajo las condiciones de frontera de continuidad del campo potencial y del desplazamiento eléctrico:
Se aplica el método de imágenes en donde se elimina el plano de tierra, se completa la esfera dieléctrica reflejando la semiesfera original y se añade un anillo de carga en la posición . Luego se soluciona la Ec.(1) teniendo en cuenta que el potencial se puede expresar separando variables como y que es válida la expansión en polinomios de Legendre [13,14]. El resultado final es:
Para todo  :
:
Donde 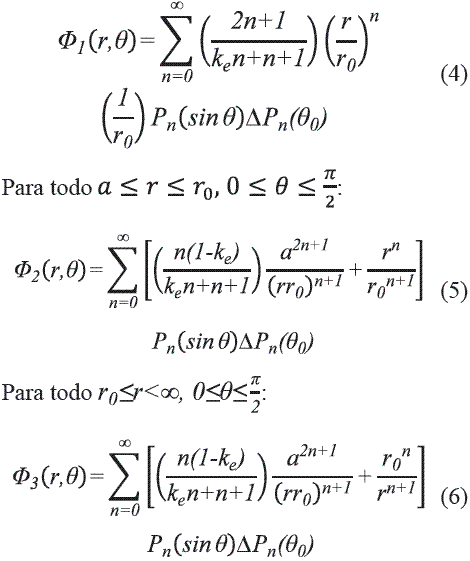 Pn (θ0) = Pn (sin θ) Pn (sin θ) y Pn (sin θ) es el Polinomio de Legendre de grado n evaluado en sin θ. A partir de las ecuaciones (4), (5) y (6) se puede obtener los campos eléctricos radiales (Er) y en la dirección θ (Eθ) para los medios 1, 2 y 3, respectivamente
Pn (θ0) = Pn (sin θ) Pn (sin θ) y Pn (sin θ) es el Polinomio de Legendre de grado n evaluado en sin θ. A partir de las ecuaciones (4), (5) y (6) se puede obtener los campos eléctricos radiales (Er) y en la dirección θ (Eθ) para los medios 1, 2 y 3, respectivamente 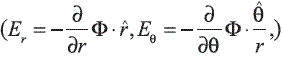 .
.
Problema de potencial constante en la punta de prueba
El modelo de punta de prueba que se utiliza toma en cuenta una discretización de la superficie como se observa en la figura 2. Con base en los resultados del literal anterior se determina el potencial en cualquier punto del espacio mediante la superposición de las contribuciones de cada uno de los anillos de carga, añadiendo el efecto de la carga de polarización inicial y carga real inicial superficial del dieléctrico. Luego, para garantizar un potencial constante en los anillos de potencial de la punta de prueba, la carga de los anillos debe satisfacer la ecuación matricial:
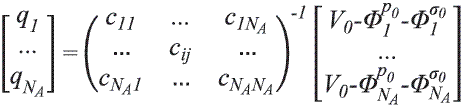
Figura 3 Sistema básico de un anillo de carga sobre una semiesfera dieléctrica que yace en un plano de tierra infinito (plano XY). El medio 1 representa la muestra dieléctrica, el medio 2 el espacio entre la muestra dieléctrica y el anillo de carga y el medio 3 más allá del anillo de carga
Donde qi es la carga del anillo de carga i; cij es el potencial por unidad de carga que produce el anillo de carga j en el anillo de evaluación de potencial i; ΦPoi es el potencial generado por la polarización inicial del dieléctrico en el anillo de evaluación de potencial i; Φσoi es el potencial generado por la densidad de carga inicial en la superficie del dieléctrico en el anillo de evaluación de potencial i; NA y es el número de anillos de carga que componen la punta de prueba.
Potencial de semiesfera dieléctrica con densidad de carga superficial real constante sobre un plano de tierra infinito
Este problema se reduce a resolver la ecuación (1) para dos regiones: el interior de la semiesfera de radio α (región 1) y el exterior (región 2) modificando las condiciones de frontera del campo potencial como sigue:
Donde u (θ) es la función escalón. Se aplica el método de imágenes completando la esfera dieléctrica y colocando una densidad de carga superficial -σ0 para  . Resolviendo (1), (8) y (9) se obtiene:
. Resolviendo (1), (8) y (9) se obtiene:
Para todo  :
:
Para todo 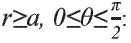 :
:
Donde 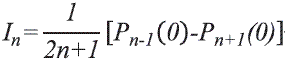 . El campo eléctrico radial y en dirección θ se calcula con el mismo procedimiento del gradiente de potencial descrito anteriormente.
. El campo eléctrico radial y en dirección θ se calcula con el mismo procedimiento del gradiente de potencial descrito anteriormente.
Potencial de una semiesfera dieléctrica con polarización constante sobre un plano de tierra infinito
Se asume una polarización inicial constante 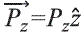 (perpendicular al plano de tierra) sobre toda la semiesfera. El planteamiento del problema es muy similar al del literal anterior, cambiando solamente la condición de continuidad de la derivada radial (Ec. (9)) en la superficie de la semiesfera de modo que:
(perpendicular al plano de tierra) sobre toda la semiesfera. El planteamiento del problema es muy similar al del literal anterior, cambiando solamente la condición de continuidad de la derivada radial (Ec. (9)) en la superficie de la semiesfera de modo que:
Se aplica el método de imágenes mediante el cual se completa la esfera dieléctrica manteniendo la polarización de la semiesfera imagen en la misma dirección y sentido. Resolviendo el sistema de ecuaciones (1), (8) y (12) se obtiene que el potencial está dado por:
Para todo
Para todo
Los campos eléctricos pueden determinarse a partir de (13) y (14).
Carga total sobre la superficie de la semiesfera dieléctrica por efectos de punta de prueba
Recuérdese que la densidad de carga inicial en la superficie de la esfera dieléctrica, ya sea real o ligada de polarización, no se ve afectada por la presencia de la punta de prueba. Por tanto, la densidad total final de carga del sistema es función de la inducción de carga de polarización adicional de la punta sobre la semiesfera. Matemáticamente la densidad de carga total está dada por:
Donde EM1r (θ, d0, V0) es el campo eléctrico radial en la superficie de la semiesfera en el medio 1(interior del dieléctrico r = a-); do es la distancia punta-muestra y Vo el potencial aplicado a la punta de prueba. La integración numérica de (15) da la carga total QT = f(d0, V0).
Fuerza electrostática sobre la punta de prueba y gradiente de fuerza
En el modelo discretizado de la punta de prueba se NA tienen anillos de carga. Para calcular la fuerza total sobre la punta se toma el promedio del campo eléctrico de los anillos de potencial adyacentes a cada anillo de carga y posteriormente se superponen todos los resultados. De esta manera se obtiene:
Donde Ez, i-1, Ez, i+1 es el campo eléctrico en los anillos de potencial adyacentes al anillo de carga qi. Para calcular el gradiente de fuerza en la dirección 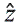 se usa la aproximación:
se usa la aproximación:
Simulación
Con base en las soluciones analíticas de la sección anterior, se hace un algoritmo en Matlab que computa todas las operaciones de las ecuaciones de potencial y campo eléctrico. A partir de éstos, se obtienen los valores de carga total sobre la superficie de la esfera, fuerza sobre la punta de prueba y gradiente de fuerza.
En la figura 4 se presenta un diagrama de flujo resumido del algoritmo. Se define un criterio de convergencia de tal manera que la variación relativa de potencial o campo eléctrico no sea superior al 2% cuando se incrementen los parámetros de ajuste, NA, Nθ y Ns; donde NA es el número de anillos de carga que conforma la punta que se debe incrementar para mejorar la respuesta; Nθ es el número de ángulos en los que se evaluará el potencial y NS es el índice de las sumatorias de las ecuaciones teóricas que, idealmente, es infinito.
La tabla 1 resume todos los valores asignados así como la inicialización de los parámetros de ajuste. Se debe aclarar que la altura de la punta hT se toma inicialmente como la altura de punta del fabricante pero se minimiza tomando un hT, efec efectivo que es menor que hT, de tal manera que no cambie el potencial en la superficie del dieléctrico en más de un 2% con respecto al potencial inicial. Los parámetros de la muestra y la punta de prueba se toman de experimentos y datos comerciales [4, 11, 12, 15]. Por otro lado para definir Ke, a, d0 y V0 se consulta [5]. Por último, los valores de σ0 y Pz se toman con base en [16, 17].
Figura 4 Diagrama de flujo resumido del algoritmo implementado en Matlab
Resultados y discusión
El criterio de convergencia, de 2%, se logra para NA = 90, Nθ = 90 y Ns = 90. Ahora se presentan los resultados más relevantes. La solución del potencial fue validada con el simulador de elementos finitos para electromagnetismo Ansoft Maxwell [18].
Influencia de la punta de prueba sobre la muestra
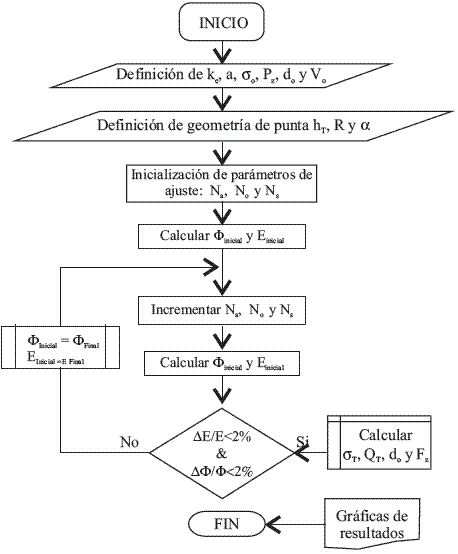
Para la geometría estudiada, se obtienen las gráficas de la figura 5 que resumen los valores de la carga total sobre la superficie del dieléctrico como función de la distancia punta-muestra y el voltaje aplicado a la punta.
Tabla 1 Definición de variables y parámetros de simulación
Se observa en la figura 5(a) que la carga total es una función lineal del voltaje aplicado a la punta independientemente de la carga superficial inicial. Esto indica que el sistema tiene una capacitancia constante que sólo depende del arreglo geométrico. Por otro lado, se puede apreciar en la figura 5(b) como la inducción de carga aumenta conforme se acerca la punta a la muestra y es comparable con la carga inicial superficial con tal intensidad que puede invertir el signo de la carga total demostrando que no se puede despreciar este efecto en la interpretación de datos de las técnicas EFM.
Figura 5 Gráficas de carga total sobre la superficie del dieléctrico con Pz = σ0 = 100μC/m2 en la curva que corresponda según la leyenda. (a) Variación de voltaje a distancia punta-muestra constante d0 = 75nm. (b) Variación de distancia punta-muestra a voltaje constante V0 = 10V
Influencia de la muestra sobre la punta de prueba
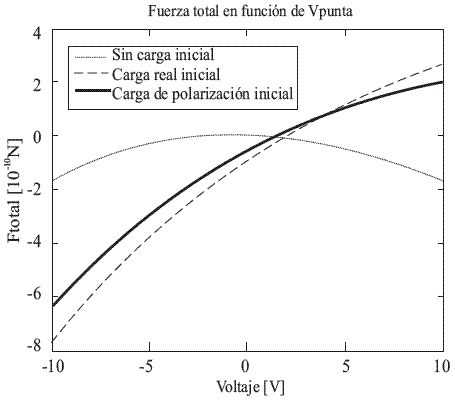
Para medir la influencia de la muestra sobre la punta de prueba se genera una gráfica que contiene la fuerza total sobre la punta en función del voltaje que se aplica a una distancia fija. En la Fig. 6 se observa cómo, para el dieléctrico sin carga inicial, las fuerzas siempre son atractivas debido a la carga inducida de signo contrario al voltaje original aplicado. Por otro lado cuando se asume una carga inicial positiva las fuerzas pueden ser atractivas o repulsivas de acuerdo al signo del voltaje que se aplique.
Figura 6 Gráfica de Fuerza sobre la punta en función del voltaje aplicado con Pz σ0 = 100μC/m2 en la curva que corresponda según la leyenda. El signo negativo implica fuerzas atractivas.
Por otro lado, se hace una validación experimental del modelo desarrollado. Para tal fin se toman los resultados de medición sobre cambio en frecuencia en la técnica EFM de medición de gradiente de campo eléctrico en una fibra dieléctrico cargado. Se parte de la ecuación de cambio de frecuencia de la viga voladiza [5]:
Donde ω0 =(62±2) kHz es la frecuencia de resonancia de la viga voladiza y k = (3±2) N/m es la constante de resorte de la viga voladiza.
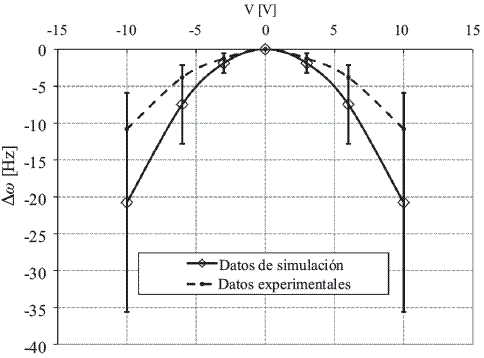
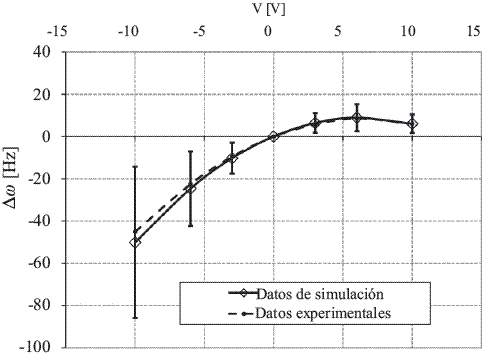
Las figuras 7 y 8, muestran el resultado experimental y teórico para los casos sin carga inicial y con carga inicial en el dieléctrico respectivamente. Se obtienen resultados que predicen los datos experimentales dentro de la barra de error determinada por la incertidumbre de la constante de resorte y la frecuencia de resonancia de la viga voladiza.
Figura 7 Gráficas de cambio de frecuencia experimental y teórica para una fibra dieléctrica cargada y una semiesfera dieléctrica, respectivamente. Ambos dieléctricos están inicialmente descargados. La barra de error pertenece al resultado de simulación
Para el caso de dieléctrico cargado, la polarización que se ajusto a los datos experimentales fue de 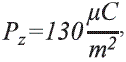 , lo cual equivale a tener una carga inicial sobre la superficie dieléctrica Qinicial = 6,38.10-16 C.
, lo cual equivale a tener una carga inicial sobre la superficie dieléctrica Qinicial = 6,38.10-16 C.
Conclusiones
El modelo teórico que se plantea y sus resultados demuestran que el efecto de inducción de carga de la punta de prueba de sobre una muestra dieléctrica no es despreciable. Este efecto puede invertir el signo de la carga superficial original. El mismo modelo permite hacer una estimación de la cantidad de carga adicional inducida así como la fuerza que se ejerce sobre la punta de prueba.
Adicionalmente, se logra predecir por primera vez de forma cuantitativa, la carga total inicial de una muestra dieléctrica con base en las curvas experimentales de cambio de frecuencia en la técnica EFM de medición de gradiente de fuerza. Se demuestra que un desplazamiento en las curvas de cambio de frecuencia implica presencia de carga en la muestra bajo análisis. Esta variación puede utilizarse para la caracterización eléctrica de estructuras.
Figura 8 Gráficas de cambio de frecuencia experimental y teórica para una fibra dieléctrica cargada y una semiesfera dieléctrica con carga ligada de polarización 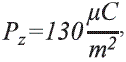 , respectivamente.
, respectivamente.
La barra de error pertenece al resultado de simulación
Como trabajo futuro, sería interesante realizar estudios dinámicos de carga sobre la muestra. Además se podrían explorar geometrías cilíndricas de muestras dieléctricas, así como variaciones de la punta de prueba.
Agradecimientos
Al Grupo de Altas Energías del departamento de Física y al Grupo de Electrónica y Sistemas de Telecomunicaciones de la Universidad de los Andes, por facilitar las herramientas computacionales utilizadas para simulación.
Referencias
1 F. J. Giessibl. "Theory of electric force microscopy in the parametric amplification regime". Physical Review B. Vol. 71. 2005. pp. 1-12. [ Links ]
2. K. L. Sorokina, A. L. Tolstikhina. "Atomic Force Microscopy Modified for Studying Electric Properties of Thin Films and Crystals. Review". Crystallography Reports. Vol. 49. 2004. pp. 476-499. [ Links ]
3. M. S. Crosser, S. H. Tessmer, R. N. Ghosh. "Scanning Electric Field Sensing for semiconductor dopant profiling". Applied Surface Science. Vol. 195. 2002. pp. 146-154. [ Links ]
4. B. Bharat (Editor). Springer Handbook of Nanotechnology. 2a ed. Ed. Springer-Verlag. Heildelberg. 2007. pp. 325-385. [ Links ]
5. J. Kim, W. Jasper, J. Hinestroza. "Direct probing of solvent-induced charge degradation in polypropylene electret fibres via electrostatic force microscopy". Journal of Microscopy, Vol. 225. 2007. pp. 72-79. [ Links ]
6. G. M. Sacha, J. J. Sáenz. "Cantilever effects on electrostatic force gradient microscopy". Applied Physics Letters. Vol. 85. 2004. pp. 2610-2612. [ Links ]
7. G. M. Sacha, C. Gómez Navarro, J. J. Sáenz, J. Gómez Herrero. "Quantitative theory for the imaging of conducting objects in electrostatic force microscopy". Applied Physics Letters. Vol. 89. 2006. pp. 173122- 173125. [ Links ]
8. S Gómez Moñivas, L. S. Froufe, R. Carminati, J. J. Greffet, J. J. Saenz. " Tip-shape effects on electrostatic force microscopy resolution". Nanotechnology. Vol. 12. 2001. pp. 496-499. [ Links ]
9. S. Gómez Moñivas, L. S. Froufe Pérez, A. J. Caamaño, J. J. Sáenz. "Electrostatic forces between sharp tips and metallic and dielectric samples". Applied Physics Letters. Vol. 79. 2001. pp 4048-4050. [ Links ]
10. W. J. Jasper, A. Mohan, J. Hinestroza, R. Barker. "Degradation Processes in Corona-Charged Electret Filter-Media with Exposure to Ethyl Benzene". Journal of Engineered Fibers and Fabrics. Vol. 2. 2007. pp 1-6. [ Links ]
11. J. Colchero, A. Gil, A. M. Baro. "Resolution enhancement and improved data interpretation in electrostatic force microscopy". Physical Review B. Vol 64. 2001. pp 245403.1-245403.11. [ Links ]
12. Mikromasch Corporation. Probe Catalog. http://www. spmtips.com/spm_probes/ Consultada el 15 de abril de 2008. [ Links ]
13. D. J. Griffiths. Introduction to Electrodynamics. Ed. Prentice-Hall Inc. New Jersey. 1999. pp.1-193. [ Links ]
14. G. Téllez. Métodos Matemáticos, Universidad de los Andes, Dpto. de Física. 2002, pp. 135-174. [ Links ]
15. Veeco Corporation, AFM Probes. https://www. ve e coprobe s . com/ s e a r ch. a sp?GroupID=42. Consultada el 20 de abril de 2008. [ Links ]
16. J. A. Malecki. "Linear decay of charge in electrets". Physical Review B. Vol. 59. 1999. pp. 9954-9960. [ Links ]
17. J. E. J. Dalley, R. S. Greenaway, Z. Ulanowski, E. Hesse, P. H. Kaye. "Measurement of the charge of airborne 3-10 μm spherical dielectric particles charged in an AC unipolar charger". Journal of Aerosol Science. Vol. 36. 2005. pp. 1194-1209. [ Links ]
18. A. Gómez. Estudio de la interacción punta-muestra dieléctrica en microscopios de fuerza atómica. Trabajo de Pregrado. Ingeniería electrónica. Universidad de los Andes. 2008. [ Links ]
(Recibido el 5 de diciembre de 2008. Aceptado el 24 de agosto de 2009)
*Autor de correspondencia: teléfono: + 57 + 1 + 691 46 26, correo electrónico: arie-gom@uniandes.edu.co (A. Gómez).